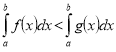Контрольні роботи "Алгебра 10-11 клас"
Контрольна робота з теми «Похідна функції».
І варіант
- (1б)Знайдіть похідну функції у=3х2.
|
А |
Б |
В |
Г |
|
6х2 |
3х |
6х |
9х |
- (1б)Обчисліть значення похідної функції ƒ(х)=х2-х в точці х0=1,5.
|
А |
Б |
В |
Г |
|
2 |
1,5 |
3 |
0,75 |
3.(1,5б)Чому дорівнює кутовий коефіцієнт дотичної до графіка функції ƒ(х)=х·ех в точці з абсцисою х0=1.
|
А |
Б |
В |
Г |
|
е+2 |
е+1 |
2е |
е |
4.(1,5б)При русі тіла по прямій відстань Ѕ (у метрах) змінюється за законом Ѕ(t)=3t2-2t+4 (t-час руху в секундах). Знайдіть швидкість тіла через 2 с після початку руху.
|
А |
Б |
В |
Г |
|
14м/с |
12 м/с |
10м/с |
8м/с |
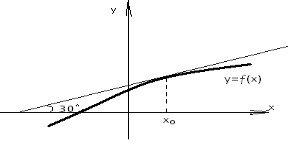
5. (1б)На малюнку зображено графік функції у=ƒ(х) та дотичну до нього в точці з абсцисою х0. Знайдіть ƒ'(х0).
|
А |
Б |
В |
Г |
|
|
|
1 |
|
6.(2б)Знайдіть похідні функцій: а) у=(х2+1)соsх; б) 
;
в) 
.
7.(2б)Складіть і розв’яжіть рівняння ƒ'(х)=-g'(х), якщо ƒ(х)=sіn2х,
g(х)=соsх+ соs
.
8.(2б) Складіть рівняння дотичної до графіка функції у=ƒ(х), яка паралельна заданій прямій
ƒ(х)=х2-6х+8; 4х+у=2.
Контрольна робота з теми «Похідна функції».
І І варіант
- (1б)Знайдіть похідну функції у=4х3.
|
А |
Б |
В |
Г |
|
64х2 |
12х2 |
12х |
4х2 |
- (1б)Обчисліть значення похідної функції ƒ(х)=х2-5х в точці х0=2.
|
А |
Б |
В |
Г |
|
-1 |
1 |
- 3 |
3 |
3.(1,5б)Чому дорівнює кутовий коефіцієнт дотичної до графіка функції ƒ(х)=
в точці з абсцисою х0=9.
|
А |
Б |
В |
Г |
|
2 |
1 |
|
3 |
4.(1,5б)При русі тіла по прямій відстань Ѕ (у метрах) змінюється за законом Ѕ(t)=2t2-3t+1 (t-час руху в секундах). Знайдіть швидкість тіла через 3 с після початку руху.
|
А |
Б |
В |
Г |
|
9м/с |
10 м/с |
4м/с |
15м/с |
5.(1б) Прямі а і b, зображені на рисунку, паралельні, причому пряма а є дотичною до графіка функції у=ƒ(х) в точці з абсцисою х0, а рівняння прямої b має вигляд 2х-у+3=0. Знайдіть ƒ'(х0).
|
А |
Б |
В |
Г |
|
-1 |
2 |
3 |
Не можна визначити |
6.(2б)Знайдіть похідні функцій: а) у=(4-х2)sіnх; б) 
;
в) 
.
7.(2б)Складіть і розв’яжіть рівняння ƒ'(х)=g'(х), якщо ƒ(х)=соs2х,
g(х)=sіnх- sіn
.
8.(2б) Складіть рівняння дотичної до графіка функції у=ƒ(х), яка паралельна заданій прямій
ƒ(х)=х2-7х+3; 5х+у=3
Контрольна робота з теми : «Застосування похідної»
І варіант
-
(1б)Скільки критичних точок на проміжку
має функція, графік якої зображено на рисунку?
|
А |
Б |
В |
Г |
|
3 |
2 |
4 |
5 |
-
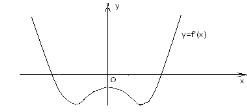(1б)На рисунку зображено графік похідної функції y=f(x), визначеної на множині дійсних чисел. Скільки проміжків спадання має функції y=f(x).
|
А |
Б |
В |
Г |
|
1 |
2 |
3 |
Не можна визначити |
-
(1б)Відомо, що для будь-якого х з проміжку для функції f виконується нерівність f'(x)>0. Порівняйте f(а) і f(b).
|
А |
Б |
В |
Г |
|
f(а) < f(b) |
f(а) > f(b) |
f(а) = f(b) |
Порівняти неможливо |
-
(1б)Яка з функцій зростає на проміжку (0;
)?
|
А |
Б |
В |
Г |
|
|
|
|
|
- (3б)Знайти критичні точки функції: а) у=х3+х2-х-1; б) у=sin2x-cosx.
-
(3б)Дослідіть функцію і побудуйте її графік
. Скільки коренів має рівняння f(x)=а у залежності від значень параметра а.
- (2б)Серед усіх рівнобедрених трикутників з бічною стороною а знайдіть трикутник з найбільшою площею.
Контрольна робота з теми : «Застосування похідної»
ІІ варіант
-
(1б)Скільки критичних точок на проміжку має функція, графік якої зображено на рисунку?
|
А |
Б |
В |
Г |
|
3 |
2 |
4 |
5 |
-
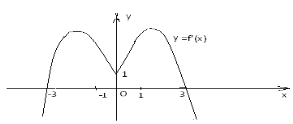(1б)Функція y=f(x) визначена на множині дійсних чисел і має похідну в кожній точці області визначення. На рисунку зображено графік функції y=f'(x). Знайти точки мінімуму функції y=f(x).
|
А |
Б |
В |
Г |
|
0 |
1; -1 |
-3 |
3 |
-
(1б)Відомо, що для будь-якого х з проміжку для функції f виконується нерівність f'(x)<0. Порівняйте f(а) і f(b).
|
А |
Б |
В |
Г |
|
f(а) < f(b) |
f(а) > f(b) |
f(а) = f(b) |
Порівняти неможливо |
-
(1б)Яка з функцій спадає на проміжку (0; )?
|
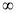А |
Б |
В |
Г |
|
|
|
|
|
- (3б)Знайти критичні точки функції: а) у=х3+2х2-4х+2; б) у=2sinx+cos2x.
-
(3б)Дослідіть функцію і побудуйте її графік :
. Скільки коренів має рівняння f(x)=а у залежності від значень параметра а.
- (2б)Серед усіх рівнобедрених трикутників з периметром 2Р знайдіть трикутник найбільшої площі.
Контрольна робота з теми : «Показникова функція»
І варіант
- (1б)Яка з даних функцій є показниковою?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
- (1б)Яка з даних функцій є зростаючою?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
(1б)Відомо, що
. Порівняйте m і n.
|
А |
Б |
В |
Г |
Д |
|
m<n |
m>n |
m=n |
m≥n |
m≤n |
-
(1б)Графік функції
перенесли паралельно на 3 одиниці вправо вздовж осі абсцис і на 2 одиниці вгору вздовж осі ординат. Графік якої функції було отримано?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
- (2б)Встановіть відповідність між рівняннями (1-3) та їх розв’язками (А-Г).
-
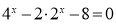А -1; 2
-
Б -2; 1
-
В 1
Г 2
- (2б)Розв’яжіть нерівність:
а) 
; б) 
.
-
(2б) Розв’яжіть нерівність:
.
-
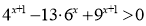(2б)Розв’язати рівняння:
.
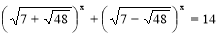Контрольна робота з теми : «Показникова функція»
ІІ варіант
- (1б)Яка з даних функцій є показниковою?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
- (1б)Яка з даних функцій є спадною?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
(1б)Відомо, що
. Порівняйте m і n.
|
А |
Б |
В |
Г |
Д |
|
m<n |
m>n |
m=n |
m≥n |
m≤n |
-
(1б)Графік функції
перенесли паралельно на 3 одиниці вліво вздовж осі абсцис і на 4 одиниці вниз вздовж осі ординат. Графік якої функції було отримано?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
- (2б)Встановіть відповідність між рівняннями (1-3) та їх розв’язками (А-Г).
-
А -1; 2
-
Б -2; 1
-
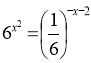В 1
Г 2
- (2б)Розв’яжіть нерівність:
а)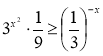 
; б) 
.
-
(2б) Розв’яжіть нерівність:
.
-
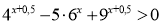(2б)Розв’язати рівняння:
.
Контрольна робота з теми: «Логарифмічна функція»
І варіант
- (1б)Серед наведених функцій укажіть зростаючу на всій області визначення:
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
(1б)Обчислити
.
|
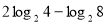А |
Б |
В |
Г |
Д |
|
-2 |
-1 |
1 |
2 |
7 |
-
(1б)Розв’яжіть рівняння
.
|
А |
Б |
В |
Г |
Д |
|
-8 |
-16 |
-2 |
-6 |
Рівняння не має коренів |
-
(1б)Знайдіть похідну функції
.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
- (2б)Установіть відповідність між виразами (1-4) і тотожно рівними їм виразами(А-Д) при a>0.
1 
А 10
2 
Б 
3 
В 
4 
Г 
Д a
-
(1б)Знайдіть значення похідної функції
у точці 
.
-
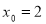(2б)Розв’яжіть рівняння: а)
; б) 
.
-
(1б)Укажіть кількість цілих розв’язків нерівності
.
-
(2б)Розв’язати рівняння:
.
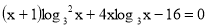Контрольна робота з теми: «Логарифмічна функція»
І І варіант
- (1б)Серед наведених функцій укажіть спадну на всій області визначення:
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
(1б)Обчислити
.
|
А |
Б |
В |
Г |
Д |
|
-2 |
-1 |
1 |
2 |
0 |
-
(1б)Розв’яжіть рівняння
.
|
А |
Б |
В |
Г |
Д |
|
1 |
0 |
-2 |
-3 |
Рівняння не має коренів |
-
(1б)Знайдіть похідну функції
.
|
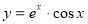А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
- (2б)Установіть відповідність між виразами (1-4) і тотожно рівними їм виразами(А-Д) при a>0.
1 
А -1
2 
Б 0
3 
В 
4 
Г 1
Д 2
-
(1б)Знайдіть значення похідної функції
у точці 
.
-
(2б)Розв’яжіть рівняння: а)
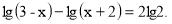; б) 
).
-
(1б) кількість цілих розв’язків нерівності
.
-
(2б) рівняння:
.
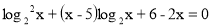Контрольна робота з теми «Інтеграл та його застосування»
І варіант
- (1б)Знайдіть загальний вигляд первісної функції ƒ(х)=3х2.
|
А |
Б |
В |
Г |
|
3х3+С |
х3+С |
х2+С |
6х+С |
-
(1б)Обчисліть інтеграл
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
(1б)Укажіть первісну функції ƒ(х)=соsх, графік якої проходить через точку А
.
|
А |
Б |
В |
Г |
|
F(х)=sіnх+5 |
F(х)=-sіnх+7 |
F(х)=sіnх+6 |
F(х)=-sіnх+6 |
- (1б)Знайдіть загальний вигляд первісної функції ƒ(х)=е 5х.
|
А |
Б |
В |
Г |
|
е 5х+С |
5е 5х+С |
|
|
-
(1б)Обчисліть площу заштрихованої фігури, зображеної на рисунку.
|
А |
Б |
В |
Г |
|
|
|
|
3 |
-
(1б)На рисунку зображено графіки функцій у=ƒ(х) і у=g(х). Порівняйте значення виразів 
і 
.
|
А |
Б |
В |
Г |
|
|
|
|
Не можна визначити |
-
(3б)Обчисліть інтеграли: а)
.
- (3б)Знайдіть площу фігури, обмеженої лініями у=-х2 +4; у=х2-2х.
Контрольна робота з теми «Інтеграл та його застосування»
ІІ варіант
- (1б)Яка з наведених функцій є первісною функції ƒ(х)=х4?
|
А |
Б |
В |
Г |
|
F(х)=4х3 |
F(х)= |
F(х)=х5 |
F(х)= |
-
(1б)Обчисліть інтеграл
.
|
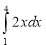А |
Б |
В |
Г |
|
15 |
30 |
-15 |
-30 |
-
(1б)Укажіть первісну функції ƒ(х)=sіnх, графік якої проходить через точку В
.
|
А |
Б |
В |
Г |
|
F(х)=-соsх+1 |
F(х)=-соsх-3 |
F(х)=соsх-2 |
F(х)=-соsх-2 |
- (1б)Яка з наведених функцій є первісною функції ƒ(х)=е -2х?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
(1б)Обчисліть площу заштрихованої фігури, зображеної на рисунку
|
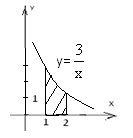
А |
Б |
В |
Г |
|
3ln2 |
3 |
ln2 |
-3ln2 |
-
(1б)На рисунку зображено графіки функцій у=ƒ(х) і у=g(х). Порівняйте значення виразів і .
|
А |
Б |
В |
Г |
|
|
|
|
Не можна визначити |
-
(3б)Обчисліть інтеграли :
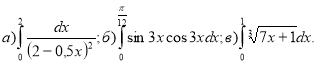
- (3б)Знайдіть площу фігури, обмеженої лініями у=х2 -4; у=-х2+2х.
Контрольна робота з теми «Елементи теорії ймовірностей і математичної статистики »
І варіант
- (1б)У меню їдальні є 3 перші страви, 6 других страв і 4 треті страви. Скількома способами можна вибрати обід, який містить по одній страві кожного виду?
|
А |
Б |
В |
Г |
Д |
|
13 |
36 |
72 |
54 |
24 |
- (1б)Гральний кубик підкинули один раз. Яка ймовірність того , що випаде число, яке кратне 3?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
1 |
|
- (1б)З натуральних чисел від 1 до 18 включно учень навмання називає одне. Яка ймовірність того, що це число є дільником числа 18?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
- (1б)Скільки трицифрових чисел з різними цифрами можна записати, використовуючи цифри 1, 2, 3, 4, 5, 6?
|
А |
Б |
В |
Г |
Д |
|
120 |
720 |
20 |
216 |
360 |
- (1б)Скількома способами можна вибрати 3 олівці та 2 ручки із 5 різних олівців і 4 різних ручок?
|
А |
Б |
В |
Г |
Д |
|
60 |
16 |
80 |
32 |
23 |
- (1б)Семеро осіб відповіли на запитання «Скільки разів за останній рік ви відвідували театр?» Відповіді були такими: 0, 2, 19, 6, 5, 2, 8. Знайдіть медіану вибірки.
|
А |
Б |
В |
Г |
Д |
|
5 |
0 |
19 |
2 |
6 |
- (2б)З 20 карток, на яких записані натуральні числа від 1до 20, вибирають навмання одну картку. Установіть відповідність між подіями (1-4) і ймовірностями цих подій (1-4).
- Число на картці ділиться націло на 4 А 0,2
2 Число на картці більше за 5 Б 0,25
3 Число на картці не ділиться націло на 5 В 0,5
- Число на картці не більше за 10 Г 0,75
Д 0,8
- (2б)Із шухляди, у якій лежать 8 жовтих і 4 зелених олівці навмання вибирають по одному олівцю, не повертаючи їх до шухляди. Яка ймовірність того, що перший вийнятий олівець буде зеленим, а другий ― жовтим.
- (2б)Учні 11-го класу проходили тестування з математики, під час якого оцінка виставлялася за 100-бальною шкалою. Середнє арифметичне оцінок учнів усього класу, в якому навчається 10 юнаків і 12 дівчат, дорівнює 90 ,а середнє арифметичне оцінок тільки юнаків дорівнює 87 балів. Знайдіть середнє арифметичне оцінок дівчат цього класу.
Контрольна робота з теми «Елементи теорії ймовірностей і математичної статистики»
ІІ варіант
- (1б)Оркестру потрібні скрипаль, піаніст і флейтист. На місце скрипаля є 7 кандидатів, на місце піаніста―5, а на місце флейтиста―2. Скільки існує варіантів нового складу оркестру?
|
А |
Б |
В |
Г |
Д |
|
14 |
35 |
50 |
70 |
10 |
- (1б)На 15 картках написані натуральні числа від 1 до 15. Яка ймовірність того, що число, записане на навмання вибраній картці, не ділиться націло ні на 2, ні на 3?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
- (1б)Яка ймовірність того, що навмання вибране двоцифрове число буде кратним числу 11?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
- (1б)Скількома способами можна сформувати комісію з 3 осіб, яких треба вибрати з 4 претендентів?
|
А |
Б |
В |
Г |
Д |
|
3 |
4 |
6 |
12 |
7 |
- (1б)Скільки двоцифрових чисел з різними цифрами можна записати, використовуючи цифри 1, 2, 3?
|
А |
Б |
В |
Г |
Д |
|
4 |
5 |
6 |
8 |
7 |
- (1б)Семеро осіб відповіли на запитання «Скільки разів за останній рік ви відвідували театр?» Відповіді були такими: 0, 2, 19, 6, 5, 2, 8. Знайдіть моду вказаної вибірки.
|
А |
Б |
В |
Г |
Д |
|
5 |
0 |
19 |
2 |
6 |
- (2б)Кидають два однакові гральні кубики, на гранях кожного з яких написані числа 1, 2, 3, 4, 5 і 6. Установіть відповідність між подіями (1-4) і ймовірностями цих подій (А-Д).
-
Сума чисел, які випали, дорівнює 3 А
2 На одному кубику випало число 3, Б 
а на іншому ― число, не менше за 3 В 
3 Сума чисел, які випали, дорівнює 4 Г 
4 На обох кубиках випало число 4 Д 
- (2б)Із шухляди, у якій лежать 8 жовтих і 4 зелених олівці навмання вибирають по одному олівцю, не повертаючи їх до шухляди. Яка ймовірність того, що перші два олівці будуть жовтими, а третій ― зеленим.
- (2б)Учні 11-го класу проходили тестування з української мови, під час якого оцінка виставлялася за 100-бальною шкалою. Середнє арифметичне оцінок 10 перших за списком учнів цього класу дорівнює 86 балів. Знайдіть середнє арифметичне оцінок решти 20 учнів цього класу, якщо відомо, що середнє арифметичне оцінок усіх 30 учнів класу дорівнює 93 бали.
Використана література
- М.І.Бурда, О.Я.Біляніна, О.П.Вашуленко, Н.С.Прокопенко
Збірник завдань для державної підсумкової атестації з математики, 11 клас. Харків «Гімназія»2009.
- В.Д.Бузько, О.М.Козлова
Алгебра і початки аналізу, збірник самостійних і контрольних робіт, 11 клас (академічний і профільні рівні). Тернопіль «Підручники і посібники», 2012.
- Ю.О.Захарійченко О.В.Школьний, Л.І.Захарійченко О.В.Школьна
Повний курс математики в тестах. ТОВ Видавництво «Ранок», 2011.
1
про публікацію авторської розробки
Додати розробку