Контрольні роботи геометрія 8 клас І семестр
Контрольна робота №1
Повторення за курс 7 класу
1 варіант
1.(0,5б) Визначте вид трикутника АВС, якщо ے А = 32 ˚, ےВ = 115 ˚, ےС =33 ˚ .
а) гострокутний; б) тупокутний; в) прямокутний; г) не можна визначити.
2. (0,5б) Скільки прямих можна провести через одну точку?
а) Жодної; б) тільки одну; в) тільки дві ; г) безліч.
3. (0,5б) Які з наведених умов 1) – 6) не є ознаками рівності двох трикутників?
1) Рівність трьох кутів; 2) рівність трьох сторін;
3) рівність двох сторін; 4) рівність двох сторін і кута, прилеглого до однієї із сторін;
5) рівність двох сторін і кута між ними; 6) рівність сторони і двох прилеглих кутів.
а) 1,2; б) 1, 3,4; в) 2,5,6; г) 1 – 6.
4. (0,5б) Центр кола, описаного навколо трикутника є точкою перетину…
а) Медіан трикутника; б) висот трикутника;
в) бісектрис трикутника; г) серединних перпендикулярів до сторін трикутника.
5. (4б) Встановити відповідність:
|
1) Один із кутів, утворених у результаті перетину двох прямих, дорівнює 124°. Знайдіть градусні міри решти кутів. |
А. 48°, 60°, 72° |
|
2) Один із суміжних кутів на 52° більший за другий. Знайдіть ці кути. |
Б. 52°, 128° |
|
3) Знайдіть кути трикутника, якщо їх градусні міри відносяться як 4:5:6 |
В. 64°, 116° |
|
4) У рівнобедреному трикутнику кут при основі дорівнює 56°. Знайдіть кути цього трикутника. |
Г. 56°, 56°, 124° |
|
|
Д. 68°, 56°, 56° |
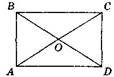
6.  (2б) У трикутнику АВС ∠С=90°, ∠А=30°, ВМ – бісектриса трикутника.
Знайдіть довжину катета АС, якщо ВМ=6см.
(2б) У трикутнику АВС ∠С=90°, ∠А=30°, ВМ – бісектриса трикутника.
Знайдіть довжину катета АС, якщо ВМ=6см.
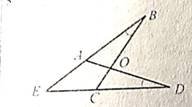
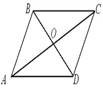
7. (2б) Дано: ЕD=ВЕ, АО=СО (рис.) Довести: ⊿АОВ=⊿СОD.
8. (2б) Коло, вписане в трикутник АВС, дотикається до сторін АВ, ВС, АС у точках D, Е, F відповідно. Відомо, що Р ⊿АВС=40см, ВЕ=6см. Знайдіть АС.
Контрольна робота №1
Повторення за курс 7 класу
2 варіант
1. (0,5б) Визначте вид трикутника АВС, якщо ے А = 92 ˚, ےВ = 45 ˚, ےС =43 ˚ .
а) гострокутний; б) тупокутний; в) прямокутний; г) не можна визначити.
2. (0,5б) Скільки прямих можна провести через дві точки?
а) Безліч; б) тільки одну; в) тільки дві; г) жодної.
3. (0,5б) Які з наведених умов 1) – 6) є ознаками рівності двох трикутників?
1) Рівність трьох кутів; 2) рівність трьох сторін;
3) рівність двох сторін; 4) рівність двох сторін і кута, прилеглого до однієї із сторін;
5) рівність двох сторін і кута між ними; 6) рівність сторони і двох прилеглих кутів.
а) 1,2; б) 1, 5, 6; в) 2,5,6; г) 1 – 6.
4. (0,5б) Точка перетину бісектрис є…
а) Центром описаного кола; б) центром вписаного кола;
в) вершиною трикутника; г) не можна визначити.
5. (4б) Встановити відповідність:
|
1) Один із кутів, утворених у результаті перетину двох прямих, дорівнює 56°. Знайдіть градусні міри решти кутів. |
А. 36°, 54°, 90° |
|
2) Один із суміжних кутів у 11 разів менший від другого. Знайдіть ці кути. |
Б. 56°, 62°, 62° |
|
3) Знайдіть кути трикутника, якщо їх градусні міри відносяться як 3:5:2 |
В. 55°, 125° |
|
4) У рівнобедреному трикутнику кут при вершині дорівнює 56°. Знайдіть кути цього трикутника. |
Г. 56°, 124°, 124° |
|
|
Д. 15°, 165° |
6. (2б) У трикутнику АВС ∠С=90°, ∠В=30°. На катеті ВС позначено точку D таку, що ∠АDС=60°. Знайдіть довжину катета ВС, якщо СD=5см.
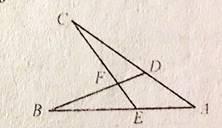
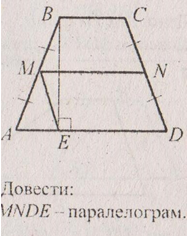
7. (2б) Дано: АВ=АС, АD=АЕ. (рис.) Довести: ⊿ВFЕ=⊿СFD.
8. (2б) Коло, вписане в трикутник АВС, дотикається до сторін АВ, ВС, АС у точках М, N, К відповідно. Відомо, що АМ=8 см, МВ=4 см, Р ⊿АВС=36см. Знайдіть АС, ВС.
Контрольна робота № 2
Многокутники
Варіант 1
Завдання 1-6 мають по 5 варіантів відповіді, серед яких лише один правильний.
1. 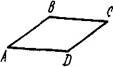 Дано
паралелограм АВСD, в якому АВ = 5 см, АD = =7 см, ∠𝐴=30°. Виберіть
правильне твердження.
Дано
паралелограм АВСD, в якому АВ = 5 см, АD = =7 см, ∠𝐴=30°. Виберіть
правильне твердження.
|
А |
Б |
В |
Г |
Д |
|
DC= 7 см |
ВС = 7 см |
∠C = 150° |
∠D > ∠B |
∠В = 30° |
2. Дано прямокутник АВСD, у якого діагональ АС = 10 см, точка О — точка перетину діагоналей. Виберіть правильне твердження.
|
А |
Б |
В |
Г |
Д |
|
ОВ = 6 см |
АО>ВО |
∠BAD > ∠𝐴BC |
ВD = 10 см |
𝐴𝐷=АО |
|
А |
Б |
В |
Г |
Д |
|
Трикутник АВС не рівнобедрений |
Периметр ромба дорівнює 28 см |
АВ може дорівнювати 6 см |
ВС > СD |
АВ=АС |
3. 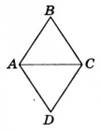 Дано
ромб АВСD, у якого АВ = 7 см. Виберіть правильне твердження.
Дано
ромб АВСD, у якого АВ = 7 см. Виберіть правильне твердження.
4. Сума двох кутів паралелограма дорівнює 220°. Знайти менший кут паралелограма.
|
А |
Б |
В |
Г |
Д |
|
110° |
80° |
70° |
35° |
75° |
5. У трикутнику АВС сторони дорівнюють 20 см, 30 см, 40 см. Знайдіть середню лінію трикутника, яка паралельна до його найбільшої сторони.
|
А |
Б |
В |
Г |
Д |
|
10 см |
15 см |
20 см |
25 см |
30 см |
6. Висота рівнобічної трапеції ділить більшу основу на відрізки 10 см та 30 см. Чому дорівнює середня лінія трапеції?
|
А |
Б |
В |
Г |
Д |
|
10 см |
15 см |
20 см |
30 см |
Визначити неможливо |
7. Діагоналі АС і ВD ромба АВСD перетинаються в точці О. ВС = 1,6 см, ВD = 2,8 см, ОВС30. Встановіть відповідність між периметрами названих фігур (1-4) та їх числовими значеннями (А-Д):
|
1) |
периметр ВОС; |
А) |
3,8 см; |
|
2) |
периметр АВС; |
Б) |
7 см; |
|
3) |
периметр многокутника АDСВО; |
В) |
6,4 см; |
|
4) |
периметр ромба АВСD. |
Г) |
4,8 см; |
|
|
|
Д) |
4 см. |
8. Діагональ рівнобічної трапеції є бісектрисою тупого кута і ділить середню лінію трапеції на відрізки завдовжки 7 см та 11 см. Знайти периметр трапеції.
9. АВСD – ромб. Знайти кут, який утвориться при перетині бісектрис кутів ВАС і ВDС.
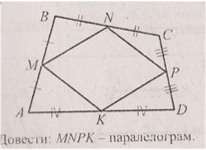 10.
10.
Контрольна робота № 2 Многокутники Варіант 2
Завдання 1-6 мають по 5 варіантів відповіді, серед яких лише один правильний. 1. Дано паралелограм АВСD, у якому О — точка перетину діагоналей, АО = 6 мм. Виберіть правильне твердження.
|
А |
Б |
В |
Г |
Д |
|
ВО > ОD |
ВО < ОD |
𝐴𝐵 ≠ 𝐷𝐶 |
АС = 12 мм |
BD = 6 мм |
|
А |
Б |
В |
Г |
Д |
|
𝐴𝐶 ≠ 𝐵𝐷 |
𝛽 = 65° |
𝛼 + 𝛾 = 60° |
ОВ < ОА |
ОВ > ОА |
2.
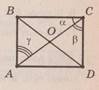 Дано прямокутник ABCD, у якому О – точка перетину
діагоналей,
Дано прямокутник ABCD, у якому О – точка перетину
діагоналей,
𝛼 = 25°. Виберіть правильне твердження.
3.
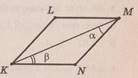 Дано ромб KLMN, у якому 𝛼
= 35°. Виберіть правильне твердження.
Дано ромб KLMN, у якому 𝛼
= 35°. Виберіть правильне твердження.
|
А |
Б |
В |
Г |
Д |
|
𝛽 = 35° |
𝐾𝑁 ≠ 𝑁𝑀 |
𝐾𝐿 < 𝑁𝑀 |
𝐾𝐿 > 𝑁𝑀 |
𝛽 ≠ 𝛼 |
4. Кути чотирикутника пропорційні числам 1,2,3,4. Знайдіть градусну міру найбільшого кута чотирикутника.
|
А |
Б |
В |
Г |
Д |
|
36° |
72° |
108° |
144° |
Інша відповідь |
5. Основи трапеції дорівнюють 20 см та 40 см. Знайти середню лінію трапеції.
|
А |
Б |
В |
Г |
Д |
|
10 см |
20 см |
30 см |
40 см |
60 см |
6. Діагоналі рівнобічної трапеції є бісектрисами її гострих кутів, а її менша основа дорівнює 6 см. Чому дорівнює бічна сторона трапеції?
|
А |
Б |
В |
Г |
Д |
|
3 см |
6 см |
9 см |
12 см |
Визначити неможливо |
7. Діагоналі АС і ВD квадрата АВСD перетинаються в точці О. АС = 8 см, ВС = 5,6 см. Встановіть відповідність між периметрами названих фігур (1-4) та їх числовими значеннями (А-Д):
|
1) 2) 3) 4)
|
периметр DВС; периметр ВОС; периметр многокутника АDСВО; периметр квадрата АВСD.
|
А) Б) В) Г) Д) |
16,8 см; 19,2 см; 24,8 см; 13,6 см; 22,4 см. |
8. Висоти паралелограма дорівнюють 8 см і 12 см, а кут між ними – 30°. Знайти периметр паралелограма.
9. У прямокутнику АВСD ВСА : DСА = 1 : 5. Відстань від точки С до діагоналі ВD дорівнює 5 см. Знайти меншу сторону прямокутника.
 10.
10.
Контрольна робота № 3. Вписані та описані чотирикутники
Варіант 2
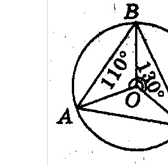
1. За даними на рисунку знайдіть градусну міру кута АВС.
|
А |
Б |
В |
Г |
Д |
|
130° |
120° |
240° |
110° |
60° |
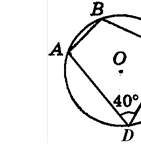
2. За даними на рисунку знайдіть градусну міру кута АВС.
|
А |
Б |
В |
Г |
Д |
|
140° |
60° |
40° |
70° |
110° |
3. Точка О – центр кола, АМВ = 120°. Встановіть відповідність між кутами (1-4) та їх градусними мірами (А-Д):
1)
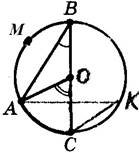 АОВ; А) 90°;
АОВ; А) 90°;
2) АВО; Б) 30°;
3) АСВ; В) 120°; 4) ВКС Г) 60°;
Д) 180°.
4. У чотирикутнику ABCD ∠𝐵𝐴𝐷 = 74°,∠𝐵𝐶𝐷 = 106°,∠𝐴𝐵𝐷 = 47°,
∠𝐶𝐵𝐷 = 58°. Знайдіть кут між діагоналями чотирикутника, який лежить проти сторони ВС.
5. Знайдіть кути чотирикутника ABCD, вписаного в коло, якщо центр кола лежить на стороні AD і ∠𝐴𝐵𝐶 = 20°, а ∠𝐷𝐵𝐶 = 10°.
6. Коло, вписане в рівнобічну трапецію, ділить точкою дотику бічну сторону на відрізки, менший з яких дорівнює 5 см. Знайдіть більшу основу трапеції, якщо її периметр дорівнює 56 см.
Контрольна робота № 3. Вписані та описані чотирикутники
Варіант 1
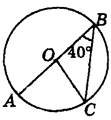
1. За даними на рисунку знайдіть градусну міру АОС.
|
А |
Б |
В |
Г |
Д |
|
140° |
40° |
90° |
60° |
40° |
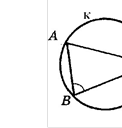
2. АМС = 80°. Знайти градусну міру дуги АВМ.
|
А |
Б |
В |
Г |
Д |
|
200° |
240° |
200° |
160° |
40° |
3. Точка О – центр кола, АВС = 30°. Встановіть відповідність між кутами (1-4) та їх градусними мірами (А-Д):
1)
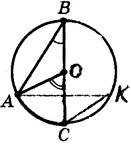 АКС; А) 90°;
АКС; А) 90°;
2) АОС; Б) 120°;
3) АОВ; В) 180°;
4) ВКС Г) 30°;
Д) 60°.
4. Чотирикутник ABCD вписано в коло. Діагональ АС цього чотирикутника є діаметром кола. Знайдіть кут між діагоналями чотирикутника, який лежить проти сторони AD, якщо ∠𝐵𝐴𝐶 = 23°, ∠𝐷𝐴𝐶 = 52°.
5. Трапецію вписано в коло, центр якого лежить на її більшій основі, кут між діагоналями дорівнює 70°. Знайдіть кути трапеції.
6. Коло, вписане в рівнобічну трапецію, ділить точкою дотику бічну сторону на відрізки, довжина більшого з яких дорівнює 8 см. Знайдіть меншу основу трапеції, якщо її периметр дорівнює 60 см.


про публікацію авторської розробки
Додати розробку
