Урок "Розв'язування прикладних на застосування теореми Піфагора"

Дата: ___/___/___                                      Клас: 8                                    Предмет: геометрія

Тема. Розв'язування прикладних  на застосування теореми Піфагора

Мета:

• освітня:

• формування математичної компетентності (формування поняття про теорему Піфагора та вироблення вмінь і навичок застосовувати набуті знання під час розв'язування пракфтичних задач);
• перевірити знання учнів з теми «Метричні співвідношення у прямокутному трикутнику. Теорема Піфагора» з метою подальшої корекції;
• використання математичних методів у життєвих ситуаціях;
• формування культури усних та письмових обчислень;
• розширити знання учнів про особистості видатних математиків;

• розвиваюча:

• формування компетентності вміння вчитися впродовж життя (формування уміння визначати мету навчальної діяльності, відбирати й застосовувати потрібні знання та способи діяльності для досягнення цієї мети;
• знаходити зв'язок з раніше вивченим: переносити набуті знання в нові ситуації);
•  стимулювання учнів до висловлювань без побоювань помилитися; формування компетентності спілкування державною мовою (формування умінь ставити запитання і розпізнавати проблему;
• міркувати, робити висновки;
•  розуміти, пояснювати і перетворювати тексти математичних задач (усно і письмово), грамотно висловлюватися рідною мовою);

• виховна:

• формування соціальної і громадянської компетентності (уміння висловлювати власну думку, слухати і чути інших, оцінювати аргументи та змінювати думку на основі доказів);
• формування компетентності ініціативності та підприємливості (формувати уміння вирішувати життєві проблеми, аналізувати, прогнозувати).

Тип уроку: удосконалення знань і вмінь

Обладнання: демонсраційно-креслярське приладдя, ілюстрації до задач

Хід уроку

I. Організаційний момент

Перевірка готовності до уроку.

ІІ. Перевірка домашньої роботи

Метод „Метеоритний дощ” (деяке розв’язання змило дощем )

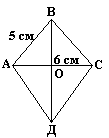
Сторона ромба рівна 5 см, а його менша діагональ рівна 6 см. Знайдіть велику діагональ ромба.

Розв’язання:

Ми знаємо що за властивістю діагоналей ромба  АС ВД и АО=ОС=3 см. Отже АОВ - прямокутний. За теоремою Піфагора – АВ²=АО ²+ ВО²,   (см.)

 ВД = 2ВО=8 (см.)

ІІІ. Актуалізація знань

Гра «Вірю – не вірю»

1.У Франції та Німеччині в епоху середньовіччя теорему Піфагора називали «ослячим мостом».

Відповідь: У Франції і деяких областях Німеччини в Середні віки теорему Піфагора називали «містком віслюка». Це  тому,  що  учнів,  які  завчили  теорему  напам’ять,  але  не  розуміли  її, називали  віслюками,  для  яких  вона  була  ніби  непрохідним  мостом.

2. Чи вірите ви , що Теорема Піфагора має 999 довдень?

Відповідь:  Теорема Піфагора  - одна з найбільш відомих і старих теорем,  має щонайменше 367 доведень.

3.     У математиків арабського Сходу ця теорема отримала назву «теореми нареченої». Чому? 

Відповідь: У математиків  арабського сходу «теорема нареченої» (Евклід називав «теорема німфи» через подібність рисунка з метеликом. Але цим словом греки називали деяких богинь. а також наречених. Перекладаючи, араби не звернули увагу на креслення і переклали слово «німфа» як «наречена», а не як «метелик»).

4.     Чи правда, що довівши свою знамениту теорему, Піфагор віддячив богам, принісши їм у жертву 100 биків?

Відповідь: Легенда говорить, що коли Піфагор сформулював І довів теорему, то приніс у жертву богам 100 биків, звідси й пішла друга назва теореми - «гекатомба» (сто биків). Але ця легенда, швидше за все, вигадана, адже він був вегетаріанцем і непримеренним супротивником пролиття крові тварин.  

5. Чи вірите ви , що в 1995 року в Єгипті було випущено поштову марку, що ілюструє теорему Піфагора

Відповідь:  ні. 1995 року в Греції було випущено поштову марку, що ілюструє теорему Піфагора. Дивлячись на неї, можна наочно пересвідчитись в тому, що в прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів.  

ІV. Удосконалення знань і вмінь

Колективне розв’язування задач

Задача 1. ( для пожежників) Якої довжини має бути драбина, щоб її можна було б приставити до вікна, що знаходиться на висоті 6 м від землі, коли відстань від нижнього кінця драбини до будинку повинна дорівнювати 2,5 см?
                                             

 Розв’язання.
Так як стіна перпендикулярна до землі драбина і стіна утворять прямокутний ∆АВС ( <С= 90°)
За теоремою Піфагора
АВ = АС² + СВ²  =
С В² = 35 + 6,25 =  42,25

СВ = 6,5 ( м)
Відповідь: 6,5 м.

Задача 2. Телевізійна вишка підтримується чотирма канатами, прикріпленими до неї на відстані 12 м від землі і на відстані 5 м від основи вишки. Скільки метрів мотузки потрібно, якщо на вузли витратили 10 м (рис. 2)?

Розв’зання

(м) – довжина однієї мотузки

13 · 4 + 10 = 62 (м)

     Відповідь. 62 м.

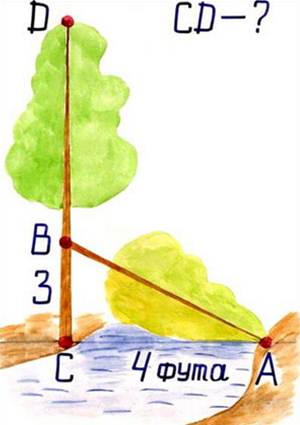
Задача 3. Задача індійського математика XII ст. Бхаскари.

На березі річки тополя росла,

Та вітру порив її стовбур зламав.

Тополя упала, і стовбур її

Кут прямий з течією річки утворив.

Пам'ятайте, у тому місці ріка

4 фути була шириною.

Верхівка схилилась до краю,

Залишивши 3 фути всього над водою.

Прошу тепер швидше скажіть мені ви:

Тополя якої була висоти?

Розв'язання

1фут = 0,3м

CВ² = 3²  + 4² = 25

CВ= 5 (футів)

CD= 5 + 3 = 8 (футів)

CD=0,3∙8=2,4 (м).

     Відповідь. 2,4 м.

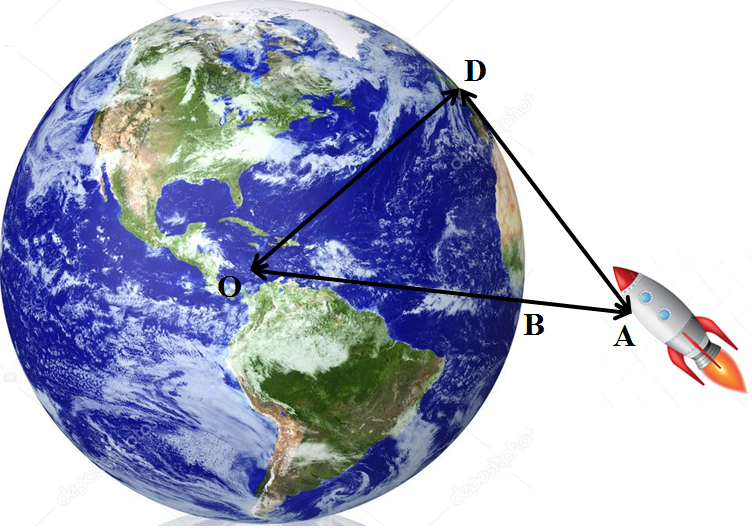
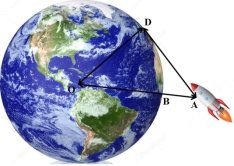Задача 4 Космонавт під час польоту знаходиться на відстані 327 км над землею. На якій відстані від корабля знаходились у цей час найбільш віддалені від нього видимі ділянки поверхні Землі? (Радіус Землі ≈ 6400 км.)

Розв’язання

АО=АВ+ВО=327+6400=6727 (км).

 (км).

     Відповідь. 2071,84 км.

Задача 5. «Дві вежі»

Дві вежі висотою 30 і 40 фунтів, розміщено одна від одної на відстані 50 фунтів. Між ними знаходиться фонтан, до якого одночасно з маківок веж з однаковою швидкістю вилетіли два голуби. Яка відстань від

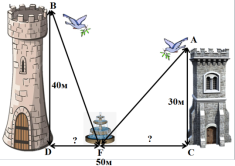фонтана до кожної з двох веж, якщо голуби долетіли до фонтана одночасно.

Дано: АС=30 (фут) ВD=40(фут) CD=50(фут) Знайти: СF; FD

Розв’язування:

AF=BF;

Нехай CF=x, FD=50-x.

Фут - довжина ступні людини.

AC 2  + CF 2  = FD2  + BD2

302  + x 2  = (50 - x)2 + 402

302 + x 2 = 502 -100x + x 2 + 402

100x = 502 - 302 + 402

100x = 20 ´ 80 + 402

100x = 1600 + 1600

x = 16 + 16

x = 32

CF  = 32(фут)

FD = 50 - 32 = 18(фут)

Відповідь: CF=32, FD=18.

V. Підсумок уроку

1. Феєрверк оцінок.

Учні самостійно оцінюють роботу учнів і виставляють оцінки.

2.  Метод «МІКРОФОН»:

- найяскравіший момент уроку…

- сьогодні на уроці я навчилась…

- мені потрібно ще повторити…

VI. Домашнє завдання

Скласти прикладну задачу за теоремою Піфагора