Контрольні роботи з алгебри, 7 клас
Контрольні роботи за курс алгебри 7 класу. Матеріали містять 5 контрольних робіт. Кожна робота складена у 2 варіантах у формі ЗНО. Робота складається з 3 частин: І частина - тестова, завдання середнього рівня складності; ІІ частина - завдання достатнього рівня; ІІІ частина - завдання високого рівня.
Контрольна робота №4 з теми «Функції».
Варіант 1.
І рівень (по 1 балу)
У завданнях 1—2 заповніть пропуски, використовуючи графік функції.
-
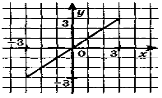 Якщо х = 2, то у = ;
Якщо х = 2, то у = ;
А) 2; Б) 3; В) 6; Г) -2.
2. Якщо у = -3, то x = ;
А) 2; Б) -3; В) 6; Г) -2.
3.Серед поданих функцій знайда лінійну функцію:
А) у = -3х +8; Б) у = 3х2 + 2; В) у = 6х3; Г) інша відповідь.
4.Функція y = kx + b зростає, якщо коефіцієнт k
А) додатний; Б) від’ємний; В) дорівнює 0; Г) інша відповідь.
5. Заповніть таблицю.
|
х |
0 |
|
1 |
|
у = х + 2 |
|
0 |
|
II рівень (по 2 бали)
6.Побудуйте графік функції . у = х – 2.
7. Знайдіть область визначення функції ![]() .
.
IIІ рівень (4 бали)
8. Не виконуючи побудови, знайдіть координати точок перетину з осями координат графіка функції у = -1,2х + 6.
Контрольна робота №4 з теми «Функції».
Варіант 2.
І рівень (по 1 балу)
У завданнях 1—2 заповніть пропуски, використовуючи графік функції.
 1.Якщо х = -2 , то у = .
1.Якщо х = -2 , то у = .
А) 2; Б) 3; В) 6; Г) -2.
2. Якщо у = 3, то х = .
А) 3; Б) -3; В) 6; Г) -2.
3.Серед поданих функцій знайда функцію пряма пропорційність:
А) у = -3х +8; Б) у = 3х2 + 2; В) у = 6х; Г) інша відповідь.
4.Функція y = kx + b спадає, якщо коефіцієнт k
А) додатний; Б) від’ємний; В) дорівнює 0; Г) інша відповідь
5.Заповніть таблицю.
|
х |
0 |
|
1 |
|
у = 2 – х |
|
0 |
|
II рівень (по 2 бали)
6.Побудуйте графік функції у = -х + 2.
7. Знайдіть область визначення функції ![]() .
.
IIІ рівень (4 бали)
8. Не виконуючи побудови, знайдіть координати точок перетину з осями координат графіка функції у = -0,5х + 6.
Контрольна робота №1 « Одночлени. Многочлени» Варіант 1
Частина І. (1 бал за завдання)
1. Спростіть вираз m+(-m+k-p)
А) (-2m-k+p); Б) (2m+k-p); B) (k-p); Г) (p-k)
2. Знайдіть значення виразу 3а+7,4, якщо а=12
А) 72; Б) 124,8; В) 43,4; Г) 19,4
3. Обчисліть (0,2)3:
А) 0,6; Б) 0,008; В) 0,8; Г) 0,08.
4. Спростіть вираз 7ху2![]() 12х3у
12х3у
А) 84х3у2; Б) 84х4у3; В) 19х4у3; ![]() Г) 84ху2х3у.
Г) 84ху2х3у.
5. Обчисліть: -3∙(![]() )2 – 0,52.
)2 – 0,52.
А) – 1 ![]() ; Б) 3
; Б) 3![]() ; В) 3
; В) 3![]() ; Г) 4
; Г) 4![]() .
.
Частина ІІ. ( по 2 бали)
6. Чи вірна рівність (- 5х3)2![]()
7. Знайдіть добуток одночленів -2,35х4у і ![]() ху4.
ху4.
Частина ІІІ. (3 бали ).
8. Спростіть вираз (-![]() ху3)3
ху3)3![]() (4у5)2.
(4у5)2.
Контрольна робота №1 « Одночлени. Многочлени» Варіант 2
Частина І. (1 бал за завдання)
1. Спростіть вираз 3∙(х –у )+3у
А) 3х; Б) (3х+2у); В) (3х+6у); Г) (3х-6у).
2. Знайдіть значення виразу 24,5-4m, якщо m=6
А) 0,5; Б) 123; В) 86; Г) 48,5.
3. Обчисліть (1/3)3
А) 1/9; Б) 1/27; В) 1/3; Г) 27.
4. Спростіть вираз -4a2b![]() 2ab:
2ab:
А) -8a3b2; Б) -8a2b; B) -8a2b; Г) -8a2bab.
5. Обчисліть: 4∙(![]() )2 –
)2 – ![]() 2.
2.
А) 8 ![]() ; Б) 2
; Б) 2![]() ; В) 2
; В) 2![]() ; Г)
; Г) ![]() .
.
Частина ІІ. ( по 2 бали)
6. Чи вірна рівність (- 4х2)3![]()
7. Знайдіть добуток одночленів (-![]() a2xy3) i (
a2xy3) i (![]() a3bx2).
a3bx2).
Частина ІІІ. (3 бали ).
8. Спростіть вираз (2![]() х3у)
х3у)![]() (
(![]() ху2)2.
ху2)2.
Контрольна робота №2 «Одночлени. Многочлени». 1 варіант
Частина І. (1 бал за завдання)
1. Знайдіть суму многочленів a+3b i 3a-3b;
А) 4а; Б) 3а2; В) 4а2; Г) 4а+6b.
2. Спростіть вираз (m3+3m)m2
А) m6+3m2; Б) m5+3m3; B) m5+3m2; Г) інша відповідь.
3. Виконати множення многочленів: (a-b)(m-n).
А) am-an-bm+bn Б) am-an-bm-bn В) am+an-bm-bn Г) інша відповідь
4.Розкладіть на множники:ax+ay.
А) a(x+y); Б) 2axy; В) a(x-y); Г) axy.
5. Розкладіть на множники: 3a(a-b)+2b(a-b).
А) (a+b)(3a-2b) ; Б) (a-b)(3a+2b); В) (3a-b)(2ab-b2) ; Г) (3a+b)(2ab+b).
Частина ІІ. ( по 2 бали)
6. Знайдіть суму многочленів 3a(a2-a+2) і 3a3-6a2.
7. Спростіть вираз: 5ах(а+5х)-9х3-4ах2
Частина ІІІ. (3 бали ).
8. Знайдіть значення виразу, попередньо спростивши його:
2m2(-3n2)+5n2m-6mn2+6m2n2, якщо m=-0.5, n=14.
Контрольна робота №2 «Одночлени. Многочлени». 2 варіант
Частина І. (1 бал за завдання)
1. Знайдіть суму многочленів 3х+5 і 7х+3:
А) 21х2+8; Б) 10х+8; В) 18х; Г) 10х+2.
2. Спростіть вираз (l2+ml)(-3ml):
А) -3ml3-3m2l2; Б) -3ml3+3m2l2; В) -3ml3-3m2l; Г) 3ml3+3m2.
3. Виконати множення многочленів: (x-y)(a-b).
А) ax+bx+ay-by ; Б) ax+bx-ay-by; В) ax-bx+ay+by; Г) ax-bx-ay+by.
4.Розкладіть на множники: 3ba-ax
А) 2abx ; Б) a(3b+x) ; В) 4abx ; Г) a(3b-x).
5. Розкладіть на множники: 6m(p-3)+5n(p-3).
А) (p-3)(6m-5n); Б) (p-3)(6m+5n); В) (p+3)(6m+5n); Г) 6mp-9.
Частина ІІ. ( по 2 бали)
6. Знайдіть суму многочленів 12х2+у2-8х2+5у2 і -10х2+6у2-5,5х2.
7. Спростіть вираз: (х+у)(х2-ху+у2)-3х3+4у3.
Частина ІІІ. (3 бали ).
8. Знайдіть значення виразу, попередньо спростивши його:
2(2-b)(b2+2b)+(2b2-4b)(b+2), якщо b=1,7
Контрольна робота №5 « Лінійні рівняння та їх системи».
Варіант 1.
1.Серед пар чисел знайти розв'язок рівняння: 2х + у = 5
А) (1; 2), Б) (2; 1), В) (2; 3), Г) (3; 2).
2. Серед пар чисел знайти розв'язок системи рівняння: 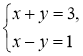
А) (1; 1), Б) (1; 2), В) (2; 1), Г) (2: 2)
3. З рівняння 3х + 4у = 12 виразіть змінну х через у.
А) х = 4 – 4у; Б) у = 3 – 3х; В) х = 4 - ![]() у; Г) у = 3 -
у; Г) у = 3 - ![]() х.
х.
4. Нехай х – перше число, а у – друге число. Серед наведених рівнянь виберіть те, яке відповідає твердженню: перше число на 5 більше від другого.
А) 5х = у; Б) х – 5 = у; В) х + 5 = у; Г) х = 5у.
5. Нехай перше число – х, а друге – у. Серед наведених систем виберіть ту, яка відповідає твердженню: сума двох чисел дорівнює 8, а їх різниця дорівнює 2.
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
6. Розв'яжіть систему рівнянь способом додавання.
![]()
7. Розв'яжіть способом підстановки систему рівнянь.![]()
8. Знайдіть два числа, якщо їх сума дорівнює13, а різниця між подвоєним першим числом і другим числом дорівнює 8.
Контрольна робота №5 « Лінійні рівняння та їх системи».
Варіант 2.
1.Серед пар чисел знайти розв'язок рівняння: 3х + у = 9
А) (1; 2), Б) (2; 1), В) (2; 3), Г) (3; 2).
2. Серед пар чисел знайти розв'язок системи рівняння: 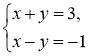
А) (1; 1), Б) (1; 2), В) (2; 1), Г) (2: 2)
3. З рівняння 3х + 4у = 12 виразіть змінну у через х.
А) х = 4 – 4у; Б) у = 3 – 3х; В) х = 4 - ![]() у; Г) у = 3 -
у; Г) у = 3 - ![]() х.
х.
4. Нехай х – перше число, а у – друге число. Серед наведених рівнянь виберіть те, яке відповідає твердженню: перше число на 5 менше від другого.
А) 5х = у; Б) х – 5 = у; В) х + 5 = у; Г) х = 5у.
5. Нехай перше число – х, а друге – у. Серед наведених систем виберіть ту, яка відповідає твердженню: сума двох чисел дорівнює 2, а їх різниця дорівнює 8.
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
6. Розв'яжіть систему рівнянь способом додавання.
![]()
7. Розв'яжіть способом підстановки систему рівнянь.
![]()
8. Знайдіть два числа, якщо їх різниця дорівнює 1, а сума першого числа та подвоєного другого числа дорівнює 19.
Контрольна робота №3 з теми «Формули скороченого множення» Варіант 1
Частина 1 ( по 1 балу)
1. Розкладіть на множники многочлен: а2-16.
А) (а-2)(а+4) Б) (а+4)(а-4) В) (4а-1)(4а+1) Г) (4а-1)(4а-1).
2. Подайте тричлен у вигляді квадрата двочлена: 9а2-6а+1.
А) (а+3)3 Б) (3а-1)2 В) (а-3)2 Г) (3а+1)2.
3. Запишіть неповний квадрат різниці виразів 2а і 3в.
А) 4а2-6ав+9в2 Б) 4а2+6ав+9в2 В) 9а2-6ав+4в2 Г) 9а2+6ав+4в2
4. Розкладіть на множники вираз: х3+8.
А) (х-2)(х2+2х+4) Б) (х-2)(х2-2х+4) В) (х+2)(х2-2х+4) Г) (х+2)(х2+2х+4)
5. Знайдіть найменше значення виразу: а2+1.
А) -1 Б) 0 В) 1 Г) 2.
Частина ІІ ( по 2 бали )
6. Розв’яжіть рівняння: х2-9=0.
7. Подайте у вигляді добутку многочленів вираз:
(2х+3)2-(х-1)2.
Частина ІІІ ( 3 бали )
8. Розв’яжіть рівняння: 9х2-4=0.
Контрольна робота №3 з теми «Формули скороченого множення»
Варіант 2.
Частина 1 ( по 1 балу)
1. Розкладіть на множники многочлен: 16а2-1.
А) (а-2)(а+4) Б) (а+4)(а-4) В) (4а-1)(4а+1) Г) (4а-1)(4а-1).
2. Подайте тричлен у вигляді квадрата двочлена: а2-6а+9.
А) (а+3)3 Б) (3а-1)2 В) (а-3)2 Г) (3а+1)2.
3. Запишіть неповний квадрат суми виразів 2а і 3в.
А) 4а2-6ав+9в2 Б) 4а2+6ав+9в2 В) 9а2-6ав+4в2 Г) 9а2+6ав+4в2
4. Розкладіть на множники вираз: х3-8.
А) (х-2)(х2+2х+4) Б) (х-2)(х2-2х+4) В) (х+2)(х2-2х+4) Г) (х+2)(х2+2х+4)
5. Знайдіть найменше значення виразу: (а+1)2.
А) -1 Б) 0 В) 1 Г) 2.
Частина ІІ ( по 2 бали )
6. Розв’яжіть рівняння: х2+9=0.
7. Подайте у вигляді добутку многочленів вираз:
(3х+2у)2-(х + у)2.
Частина ІІІ ( 3 бали )
8. Розв’яжіть рівняння: 4х2-9=0.


про публікацію авторської розробки
Додати розробку
