Алгебра і початки аналізу 10 клас Тема уроку. Знаходження найбільшого і найменшого значень функції

Алгебра і початки аналізу 10 клас

Тема уроку. Знаходження найбільшого і найменшого значень функції

Мета: формування знань учнів про алгоритм знаходження найбільшого і найменшого значень функції.

Очікувані результати: учні повинні обчислювати найбільше і найменше значення функції на відрізку, розв’язувати нескладні прикладні задачі на знаходження найбільших і найменших значень реальних величин.

Основні поняття: найбільше і найменше значення функції на відрізку.

Компетентності, що формуються: математична – уміння оперувати числовою інформацією, обчислювати найбільше і найменше значення функції на відрізку, розв’язувати нескладні прикладні задачі на знаходження найбільших і найменших значень реальних величин; ключові – інформаційно-цифрова; соціальна і громадянська; спілкування державною мовою; уміння вчитися впродовж життя.

Обладнання: підручник, роздавальний матеріал.

Тип уроку: засвоєння нових знань і вмінь.

ХІД УРОКУ

І. Організаційний момент

ІІ. Перевірка домашнього завдання

Учитель пропонує учням самостійно перевірити правильність виконання домашнього завдання за графіками, заздалегідь підготовленими на дошці.

ІІІ. Актуалізація опорних знань

Фронтальна бесіда за готовим рисунком.

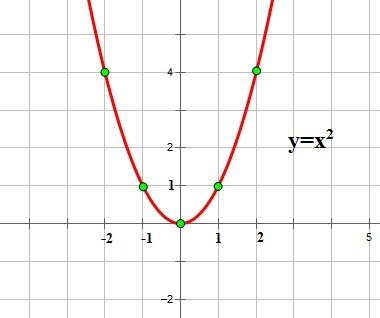
На рис.1 зображено графік квадратичної функції у=. Укажіть: 

1. Найменше значення функції на проміжку: а) 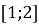; ; 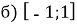в) 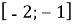, і точки, у яких воно досягається;
2. Найбільше значення функції на проміжку:  а) 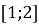; ; 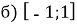в) 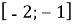, і точки, у яких воно досягається.

ІV. Формулювання теми, мети й завдань уроку; мотивація навчальної діяльності

Слово вчителя

 Людині в житті часто доводиться шукати найкращий, або, як часто кажуть, оптимальний розв’язок поставленої задачі. Частину таких задач вдається розв’язати за допомогою методів математичного аналізу – це задачі, які можна звести до знаходження найбільшого або найменшого значення функції.

Уявіть, що організація отримала замовлення: розрахувати розміри відкритого басейну об’ємом 108 , що має квадратне дно. На облицювання стін і дна басейну має бути витрачено мінімальну кількість матеріалу. Сьогодні у нас є можливість навчитися виконувати такі розрахунки, застосовуючи алгоритм знаходження найбільшого і найменшого  значень функції.

V.  Усвідомлення і осмислення правила обчислення най­більшого і найменшого значення функції на відрізку.  Шкільна лекція

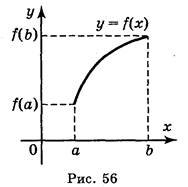
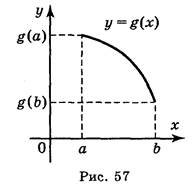Розглянемо рисунки 56 і 57, на яких зображено графіки функції у = f(x) і у = g(x), 

заданих на відрізку [а; b].

Функція у = f(x) зростає, а функція у = g(x) спадає. На відрізку [а; b] найменше значення функції у = f(х) дорівнює f(a), а найменше значення функції у = g(x) дорівнює g(b). Відповідно найбільші значення цих функцій на даному відрізку дорівнюють f(b) та g(a). Отже, якщо функція неперервна і зростає (спадає) на дея­кому відрізку, то найбільше і найменше значення функція набу­ває на кінцях цього відрізка.

Розглянемо рисунок 58, на якому зображено графіки трьох функцій. Аналіз цих графіків свідчить, що найбільше і наймен­ше значення функцій неперервних і диференційованих на про­міжку [а; b] досягаються цими функціями або на кінцях відрізка, або в критичних точках.

Отже, неперервна і диференційована функція на заданому відрізку приймає найбільше і найменше значення в критичних точках або на кінцях відрізка.

Таким чином, якщо функція у = f(x) неперервна на відрізку [а; b] і має похідну в кожній внутрішній точці цього відрізку, то для знаходження найбільшого і найменшого значень функції на відрізку [а; b] треба:

1) знайти значення функції на кінцях проміжку, тобто числа f(a) і f(b);

2) знайти значення функції в тих критичних точках, які на­лежать проміжку [а; b];

3)   із знайдених значень вибрати найбільше і найменше.

VІ. Осмислення нового матеріалу

Колективне виконання завдань під керівництвом учителя.

Приклад 1. Знайдіть найбільше і найменше значення функції f(x)=2+ на відрізку [0

Колективне розв’язання під керівництвом учителя.

D(f)=R, отже, відрізок [0входить до області визначення функції f(x).

f '(x)=2 - 2.

f '(x) існує на всій області визначення функції f (x), отже, функція f (x) є неперервною на заданому відрізку;

f '(x)=0, 2 - 2 =0, - 2=0, 2)=0,

=0 або 2=0;

                     =1/2,

 х= х=(+ n€Z – критичні точки.

У заданий відрізок попадають тільки критичні точки: ,,.

f()=, f()=1, f()=, f(0)=1,   f ()=1.

= f() = f()= =1,5;

= f()= f(0)= f ()=1.

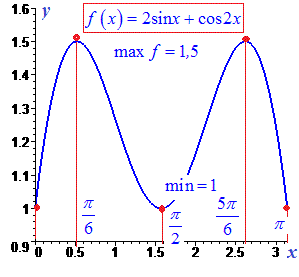
Відповідь: 1,5; 1.

Учитель. Велика кількість практичних задач зводиться до знаходження найбільшого і найменшого значень функції на проміжку.

Під час розв’язування таких задач діємо за схемою:

1. Вибрати «зручну» змінну х, через яку потрібну величину виразити як  f(x).
2. Знайти найбільше або найменше значення цієї функції на деякому проміжку.
3. З’ясувати, який практичний зміст мають отримані результати. 

Повернемось до задачі з басейном. Тепер є можливість зробити необхідний розрахунок. Нехай довжина сторони квадрата (дна басейну) дорівнює х (х>0), тоді його висоту можна виразити як , тобто . Нехай площа, що нас цікавить, S. Тоді S=+. Розглянемо функцію S(х)=+. S'(х)=2x-. Знайдемо критичні точки функції: 2x-=0;

=216; х=6.

Отримана точка х=6 є точкою мінімуму, єдиною для S(х). Таким чином, у ній і буде найменше значення функції S(х). Отже, найменші розміри басейну такі: х=6 м – сторона квадратного дна, 108:36=3 м – висота. Відповідь: 6 м; 3 м.

VІІ. Підбиття підсумків уроку

Бліцопитування

1. Що нового дізналися на уроці?
2. Опишіть алгоритм знаходження найбільшого і найменшого значень функції на проміжку.
3. Чи можна знайти найбільше (найменше) значення квадратичної функції, не застосовуючи методи математичного аналізу?

VІІІ. Домашнє завдання

П.5.3 (прочитати), ст..90 №1(1) №2(2),№5.