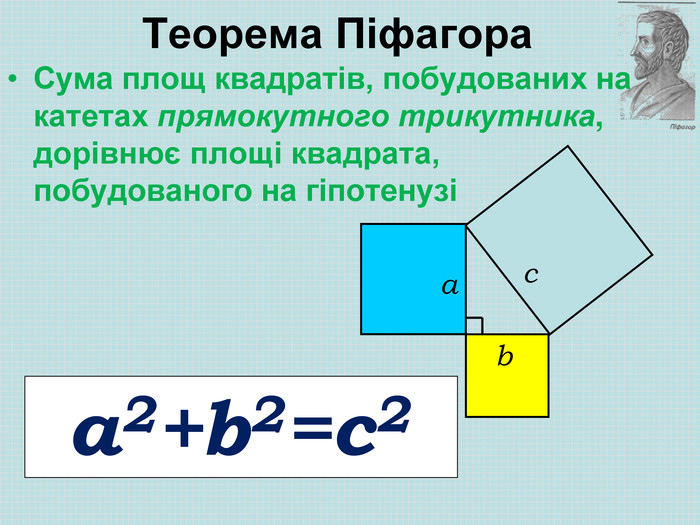
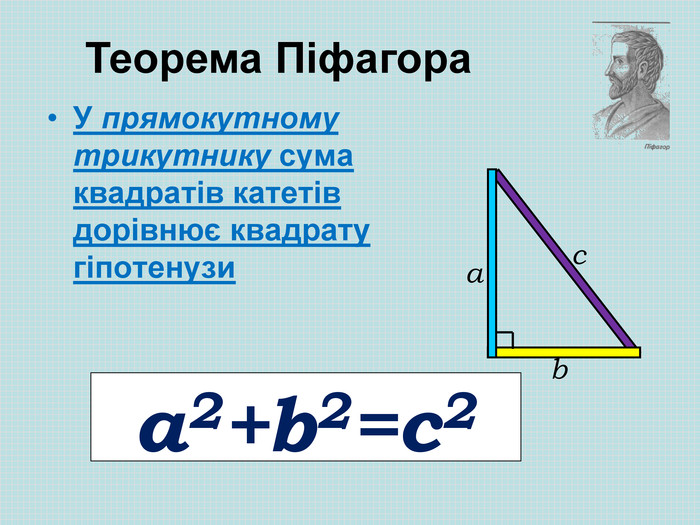
Презентація Теорема Піфагора

У геометрії є два скарби: перший – теорема Піфагора, другий – золотий поділ. Перший можна порівняти з мірою золота, другий – із коштовним каменем Йоганн Кеплер

Сучасних науковців цікавить питання: «Чи існує життя на Марсі?» І серед інших було прийняте рішення передати жителям Марса сигнал у вигляді теореми Піфагора.

Рівність 3І + 4І = 5І була відома єгиптянам  ще близько 2300 р. до н. е…  На думку Кантора, німецького історика  математики, «натягувачі  мотузок» будували прямі кути за допомогою  прямокутного трикутника із сторонами 3, 4 і 5 одиничних відрізків.

Єгипетський трикутник 32+42=52 3:4:5

Піфагор народився: близько 580 р. до н. е. у Греції, на острові Самос у сім’ї золотих справ майстра Мнесарха. За легендою оракул пророчив йому та його дружині народження сина, який буде славитися віками своєю мудрістю, справами та красою. Пророцтво збулося.

У молоді роки Піфагор виїхав до Єгипту вивчати науки. Під час завоювання Єгипту Персією його захопили в полон і вивезли до Вавілона. У Вавілоні Піфагор вивчив, крім математики, астрономію та астрологію.

Здобувши широкі знання з природничих наук, повернувшись на батьківщину, він створив свою наукову школу в м. Кротон – піфагорійський союз.

Піфагор навчав медицині, принципам політичної діяльності, астрономії, математиці, музиці, етиці. У школі Піфагора вперше був виказаний здогад щодо кулястості Землі.

Центральне місце в філософії вихованців Піфагора займали числа: “Саме мудре - це число” Для учнів Піфагора «4» було священним числом. Числа 6 і 28 вважались досконалими, вони і були паролем піфагорійців.

Це був одночасно і релігійний союз, і політичний клуб, і наукове товариство. Всі учні Піфагора і він сам були працелюбні.

За статутом у школу приймали лише тих, хто вмів зберігати таємниці, був стриманим, зосередженим і давав обітницю мовчати.

Емблемою союзу була пентаграма-п‘ятикутна зірка, символ здоров’я і досконалості, опізнавальний знак піфагорійців. Вона має поворотну симетрію п‘ятого порядку, тобто має п'ять осей симетрії

В «Золотих віршах» Піфагор показав ті моральні правила, суворе виконання яких призводить до ідеалу. Ось декілька з них: Роби лише те, що в результаті не засмутить тебе і не примусить каятися. Не роби ніколи того, чого ти не знаєш. Але навчися усього, що варто знати, і тоді будеш вести спокійне життя. Не зневажай здоров’ям свого тіла. Доставляй йому вчасно їжу і питво, і вправи, без яких воно бідує. Привчайся жити просто, без розкоші.

Не закривай очей, коли хочеться спати, не проаналізувавши успіх своїх вчинків за минулий день. Не приймай під свій дах балакунів і легковажних людей. Усе впорядковується відповідно до чисел. Лише не благородна людина здатна в очі хвалити, а поза очі злословити. Тимчасова невдача краще тимчасової удачі. Твори велике, не обіцяючи великого. Живи з людьми так, щоб твої друзі не стали недругами, а недруги стали друзями.

Деякі повчання Піфагора були записані у формі афоризмів Не проходьте мимо терезів – не порушуйте справедливості; Не сідайте на подушку – не зупиняйтеся на досягнутому; Не гризіть свого серця – не піддавайтесь меланхолії; Не поправляйте вогонь мечем – не роздратовуйте тих, хто і так у гніві;

…У Франції та Німеччині в епоху середньовіччя теорему Піфагора називали «ослячим мостом» Учнів, що запам’ятовували теорему без розуміння, називали віслюками, оскільки вони не могли перейти через міст – теорему Піфагора.

Теорема Піфагора Сума площ квадратів, побудованих на катетах прямокутного трикутника, дорівнює площі квадрата, побудованого на гіпотенузі а c b а2+b2=с2

У прямокутному трикутнику сума квадратів катетів дорівнює квадрату гіпотенузи Теорема Піфагора а c b а2+b2=с2

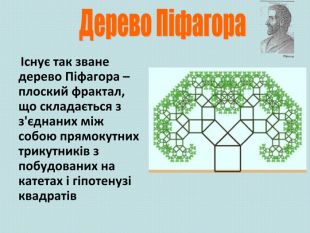
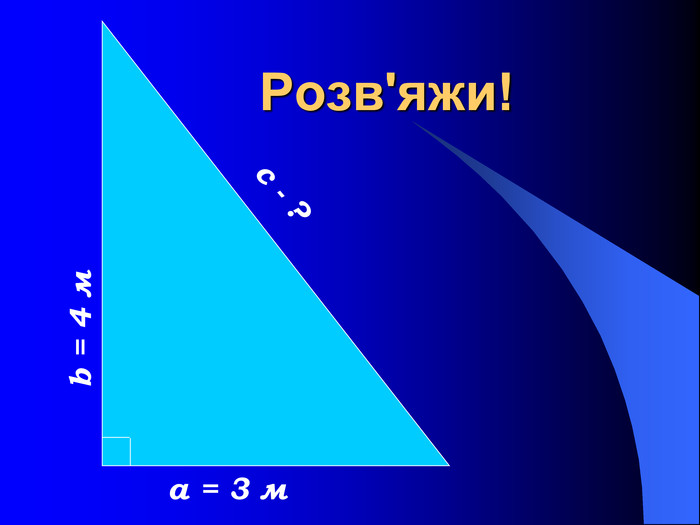
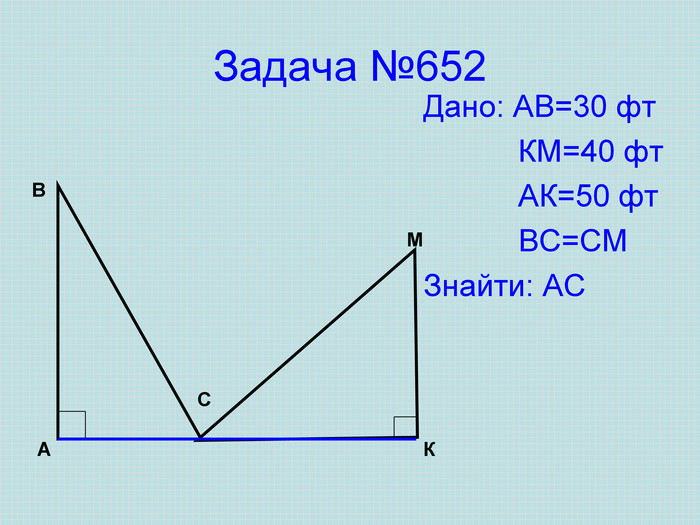
На сьогодні у науковій літературі  зафіксовано 367 доведень даної теореми . Ймовірно, теорема Піфагора є єдиною теоремою з настільки значним числом доведень. Таке різноманіття можна пояснити лише фундаментальним  значенням  теореми для  геометрії.  Найвідоміші з них: доведення методом площ

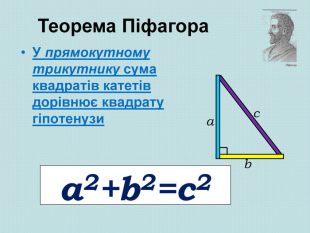
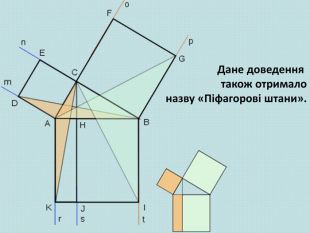
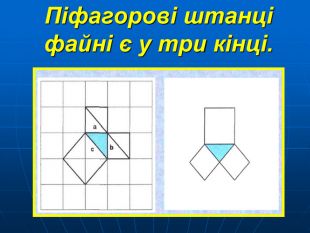
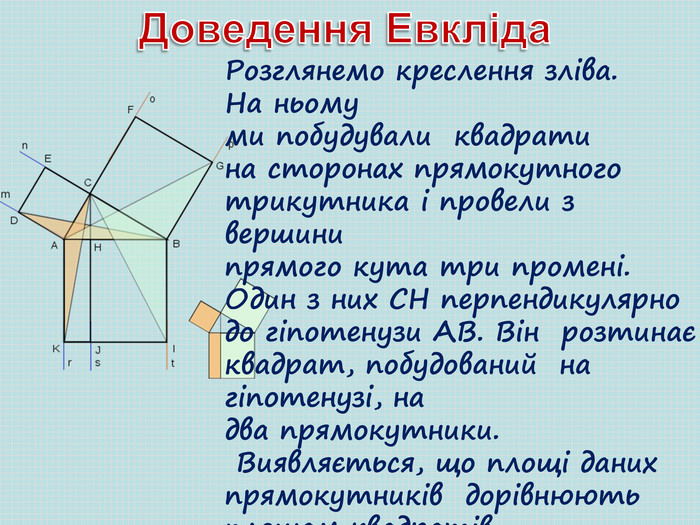
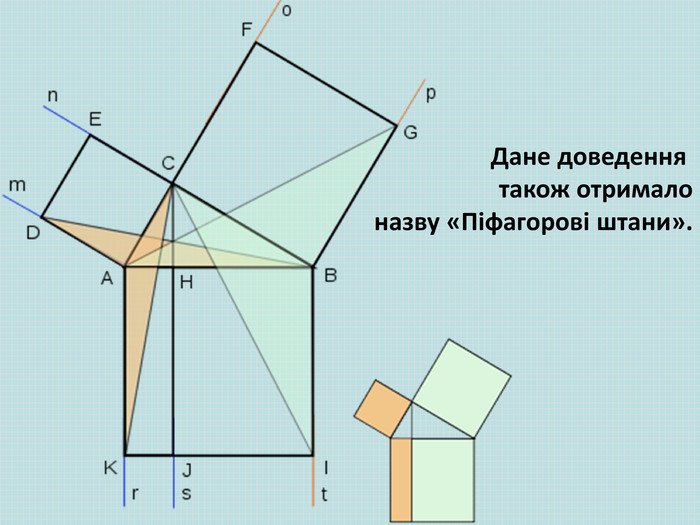
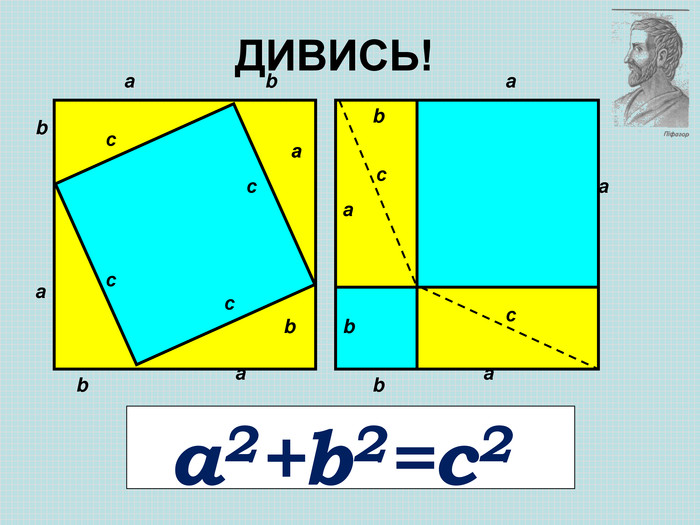
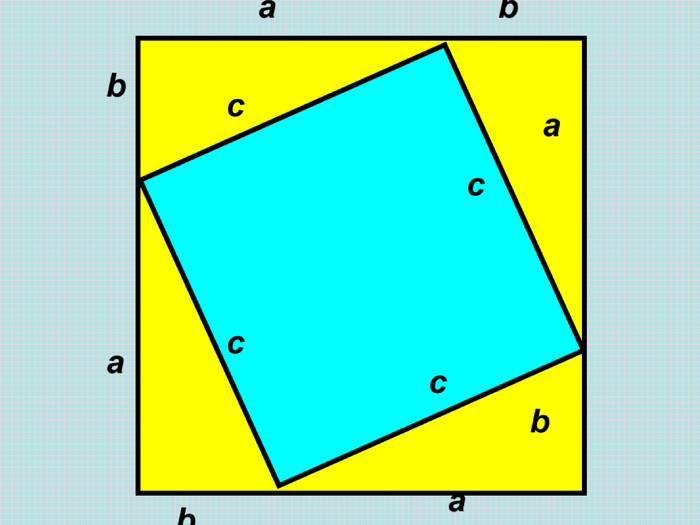
Розглянемо креслення зліва.  На ньому ми побудували  квадрати  на сторонах прямокутного  трикутника і провели з вершини  прямого кута три промені. Один з них СН перпендикулярно  до гіпотенузи АВ. Він  розтинає  квадрат, побудований  на гіпотенузі, на два прямокутники.  Виявляється, що площі даних  прямокутників  дорівнюють  площам квадратів, побудованих на  відповідних  катетах.

Дане доведення  також отримало назву «Піфагорові штани».

ДИВИСЬ! а а а а а а а а b b b b b b b с с с с с с а2+b2=с2

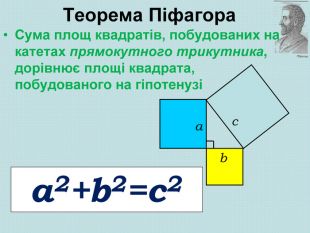
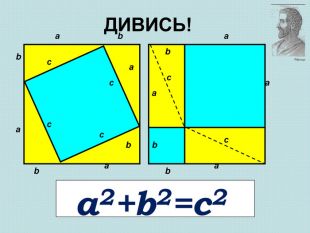
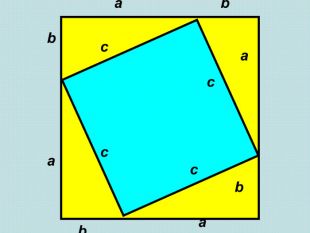
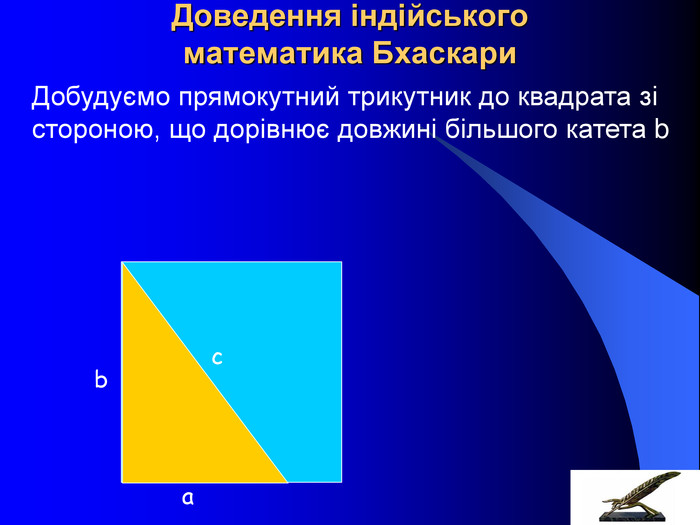
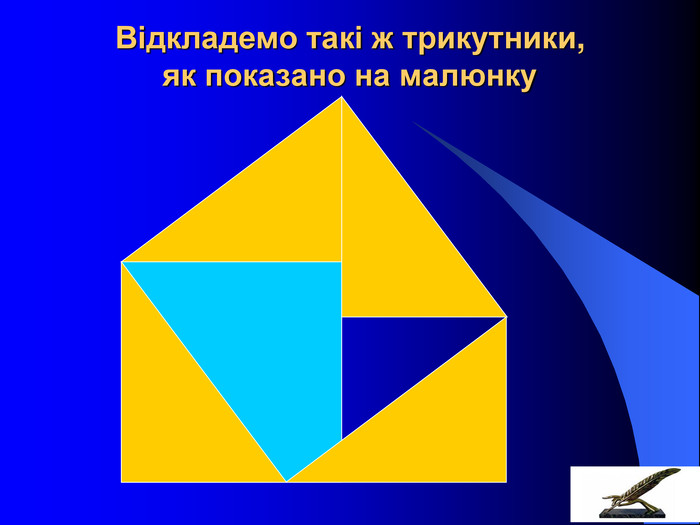
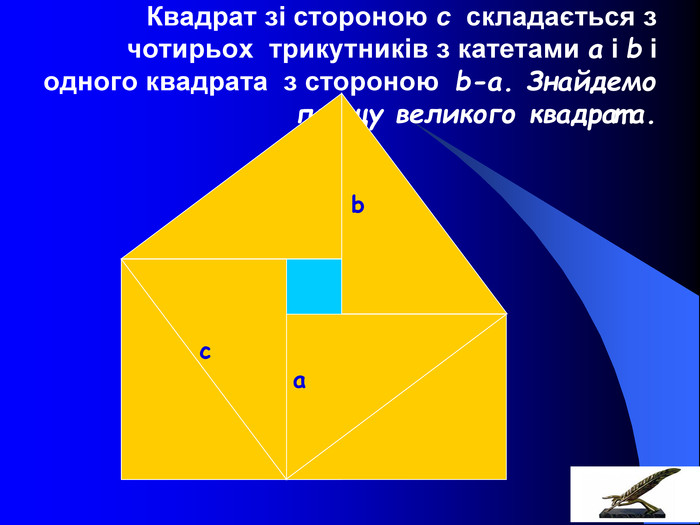
Розташуємо чотири рівних прямокутних  трикутники так, як показано на малюнку. 2) Чотирикутник зі сторонами с є квадратом, оскільки сума двох гострих кутів 90°, а розгорнутий кут -180°. 3)Площа всієї фігури рівна, з одного боку, площі квадрата зі стороною (а + в), а з іншого боку, сумі площ чотирьох трикутників і площі  внутрішнього квадрата. S=(a+в)2; S=4ав/2+с2; (a+в)2 =4ав/2+с2; а2 +2ав+в2 =2ав+с2; а2 +в2 =с2, Що й треба було довести.

Доведення Джеймса Гарфілда (двадцятий президента США, 1880р) Елекова Э.М. Республика Алтай * b b a a c c Площу трапеції з основами а і в, і висотою а+в можна обчислити двома способами: S= (a+b)2/2; S= 2(ab/2) + c2/2; (а2+2ав+в2)/2=ав+с2/2; а2/2+ав+в2/2=ав+с2/2; /·2; а2+в2=с2.

Доведення індійського математика Бхаскари Елекова Э.М. Республика Алтай * a b c Добудуємо прямокутний трикутник до квадрата зі стороною, що дорівнює довжині більшого катета b

Відкладемо такі ж трикутники, як показано на малюнку Елекова Э.М. Республика Алтай *

На малюнку є квадрат, площа якого дорівнює b2 і є квадрат, площа якого дорівнює c2 Елекова Э.М. Республика Алтай *

Квадрат зі стороною с складається з чотирьох трикутників з катетами a і b і одного квадрата з стороною b-a. Знайдемо площу великого квадрата. Елекова Э.М. Республика Алтай * a b с

Великий квадрат складається з чотирьох рівних прямокутних трикутників з катетами а і b і одного квадрата з стороною b-a тобто, с2=4∙Sтр + (b-a)2= = 4∙(ab/2) + (b-a)2= = 2ab + b2 - 2ab + a2 = = a2 + b2 Отже, с2 = a2 + b2 , що й треба було довести Елекова Э.М. Республика Алтай *

Розв'яжи! а = 3 м b = 4 м с - ?

Розв'яжи! b = 6 дм с = 10 дм а - ?

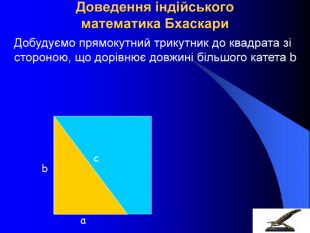
Часто математики записували свої завдання у віршованій формі. Ось одне із завдань індійського математика XII ст. Бхаскари: 1. На березі річки тополя росла І вітру порив її стовбур зламав. Тополя упала і стовбур її Кут прямий з течією ріки утворив. Пам’ятай, в тому місці ріка Чотири фути була шириною. Верхівка схилилась до краю, Залишивши три фути всього над водою. Прошу, тепер швидше скажи мені ти: Тополя якої була висоти? Старовинна задача

Розв'язання: 4 3 ? X2 =32 + 42; X2 = 25; X = 5. Отже 5 футів – довжина відломленої частини стовбура; 3 + 5 = 8(футів) – висота тополі.

Старовинна задача ? 2. Сталося якомусь чоловіку до стіни драбину поставити, стіни ж тої висота є 117 стоп. І відати хоче він, на скільки стоп драбини нижній кінець від стіни отстояти має, якщо драбини довжина 125 стоп.

? 125 117 х 1252 = 1172 + Х2 ,або X2 = 1252 – 1172; X2 = (125 – 117)(125 + 117); X2 = 8·242; X2 = 4·4·121; X = 2·2·11; X = 44. На 44 стопи нижній кінець драбини віддалений від стіни Розв'язання: Ця задача з першого підручника математики на Русі. Називається цей підручник «Арифметика», а видав його Леонтій Пилипович Магніцький.

Задача №652 Дано: АВ=30 фт КМ=40 фт АК=50 фт ВС=СМ Знайти: АС А В М К С

Діагональ d квадрата із стороною а можна розглядати як гіпотенузу прямокутного рівнобедреного трикутника з катетом а, тобто d2 = а2 +а2; Таким чином d2=2a2; звідси d=

Висоту h рівностороннього трикутника із стороною а можна розглядати як катет прямокутного трикутника, гіпотенуза якого а, а інший катет а/2 Таким чином маємо: Звідси випливає або

Малюнок до теореми для випадку рівнобедреного прямокутного трикутника називали “піфагоровими штанами”. «Пифагоровы штаны на все стороны равны»

іноді цей малюнок зображали у вигляді різних смішних фігурок

Піфагорові штанці файні є у три кінці.

Хто в сорочці Піфагора – піднось руки вгору !

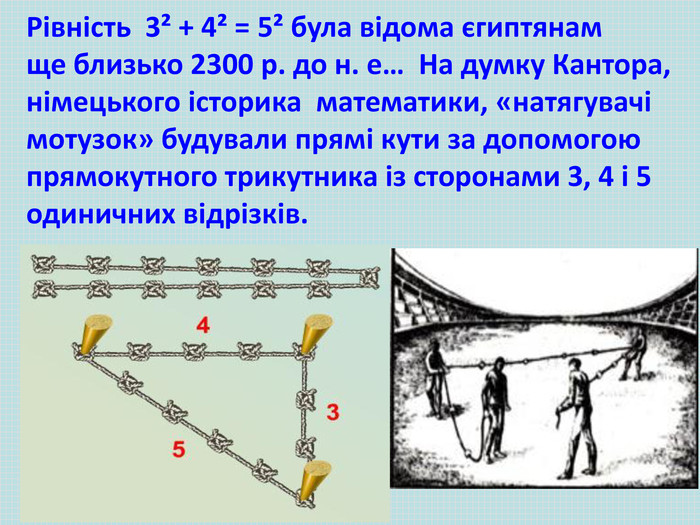
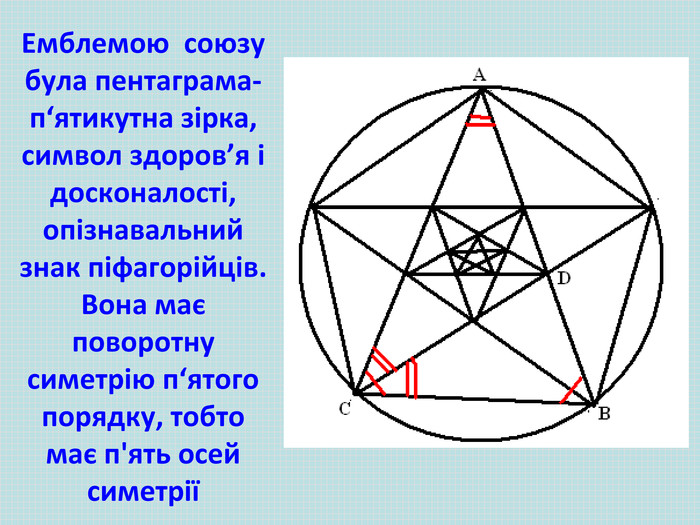
Піфагор вважав, що число 12 несе щастя, а 13 – нещастя, 5 символізує колір, 6 – холод, 7 – розум, здоров’я та світло, 8 – кохання, 9 – постійність. Особливо ненависними піфагорійцям були числа 13 та 17. Великий вчений и математик Піфагор за допомогою нумерологічних таблиць, довів, що наша доля, життя закладені в дату нашого народження.

На персні Піфагора було викарбувано такий девіз: «Тимчасова невдача краща тимчасової удачі».

…Піфагор був переможцем на 58-х олімпійських іграх з кулачного бою. Олімпійським чемпіоном він був чотири роки поспіль

Про виняткову популярність Піфагора свідчать монети з його зображенням.

Існує так зване дерево Піфагора – плоский фрактал, що складається з з'єднаних між собою прямокутних трикутників з побудованих на катетах і гіпотенузі квадратів

У Греції була випущена поштова марка з нагоди перейменування острова Самос в острів Піфагорейон.

Теоремі Піфагора та його учням присвячені вірші, пісні, малюнки, картини. Так, художник Ф.А. Бронніков (1827 – 1902) намалював картину «Гимн пифагорейцев восходящему солнцу»

Пам'ятник Піфагору знаходиться в порту Піфагорія і нагадує всім про теорему Піфагора.

Геометрія володіє двома скарбами: один з них – це теорема Піфагора, яку можна порівняти з мірою золота

За що ти можеш себе сьогодні ПОХВАЛИТИ? Що тобі ВДАЛОСЯ сьогодні на уроці? Над чим ще потрібно ПОПРАЦЮВАТИ? Навіщо нам був потрібний цей урок?

Життя – театр, а всі ми в нім актори, Ми знаємо багато різних див, Та пам’ятати будем Піфагора, Що теорему «золоту» створив.

Домашнє завдання:

Дякую за урок!

«Причина популярності теореми Піфагора триєдина – це краса, простота і значущість".