Контрольні роботи залгебри 9 клас
Завдання для контрольних робіт призначені для оцінювання навчальних досягнень учнів 9 класу з алгебри. Завдання згруповані за чотирма рівнями і дозволяють якісно і ефективно здійснювати оцінювання знань учнів диференційовано. Завдання початкового та середнього рівнів навчальних досягнень учнів подані у тестовій формі. Цінність таких завдань полягає у тому, що вони не тільки дають можливість оперативно контролювати знання учнів, а й сприяють виробленню в учнів навичок виконувати тестові завдання, самоконтролю.

Управління освіти
Бахмутської міської ради
Донецької області
Методичний кабінет
АЛГЕБРА
КОНТРОЛЬНІ РОБОТИ 9 КЛАС
Творча група
Керівник групи:
Щеглова О.М.-вчитель ЗОШ№10
Члени групи:
Махіборода І.В.-вчитель ЗОШ№10
2017
Рецензент: Т.В. Лисиченко, керівник міського методичного об’єднання вчителів математики
Контрольні роботи з алгебри. 9 клас.
Завдання для контрольних робіт призначені для оцінювання навчальних досягнень учнів 9 класу з алгебри. Завдання згруповані за чотирма рівнями і дозволяють якісно і ефективно здійснювати оцінювання знань учнів диференційовано. Завдання початкового та середнього рівнів навчальних досягнень учнів подані у тестовій формі. Цінність таких завдань полягає у тому, що вони не тільки дають можливість оперативно контролювати знання учнів, а й сприяють виробленню в учнів навичок виконувати тестові завдання, самоконтролю.
Посібник містить контрольні роботи, самостійні роботи, та математичні диктанти з усіх тем курсу алгебри 9 класу.
ЗМІСТ
Передмова_____________________________________________________5
Діагностична контрольна робота ________________________________6
Тема№1: Нерівності та їх властивості. Лінійні нерівності з однією змінною___________________________________________________________10
Тема№2: Системи лінійних нерівностей з однією змінною______________16
Тема№3: Функція та її властивості.Квадратична функція та її графік__21
Підсумкова контрольна робота за І семестр з алгебри у 9-х класах____30
Тема№4: Нерівності другого степеня з однією змінною.Розв’язування нерівностей методом інтервалів.Системи рівнянь з двома змінними____32
Тема№5: Елементи прикладної математики_________________________37
Тема№6 :Числові послідовності.Арифметична і геометрична прогресії___42
Підсумкова контрольна робота……………………………………..……….49
Література__________________________________________________51
Передмова
Даний посібник містить добірку завдань для проведення оцінювання знань, умінь та навичок з алгебри учнів 9-го класу.
Зміст посібника відповідає чинній програмі Міністерства освіти і науки України.
Основна мета даного видання – допомогти вчителю провести контроль знань учнів за 12-бальною системою.
Кожне завдання для перевірочних робіт розраховане на один урок.
Завдання для перевірочних робіт подані у двох варіантах. Завдання кожного варіанта згруповані за чотирма рівнями. Початковий та середній рівні подано у формі тестів, які включають основні поняття даної теми і мають алгоритмічний характер. З чотирьох запропонованих відповідей тільки одна є правильною. Тестові завдання вважаються виконаними правильно, якщо в роботі учень вибрав тільки одну букву, якою позначена правильна відповідь. При цьому учень має право наводити будь-які міркування, що пояснюють його вибір відповіді, але це необов’язково.
При виконанні завдань достатнього рівня навчальних досягнень учнів розв’язання цих завдань супроводжується необхідними обґрунтуваннями. Ці завдання посильні для більшості учнів і дають можливість отримати 7 – 9 балів. При виконанні завдань високого рівня учень має вибирати раціональний шлях розв’язування, продемонструвати нестандартне мислення, повні логічні обґрунтування всіх завдань.
Можна змінити обсяг і зміст завдань, враховуючи індивідуальні особливості учнів класу, стан їх підготовленості, але сума балів за роботу має дорівнювати 12.
Діагностична контрольна робота
Варіант 1
1.Завдання з вибором однієї правильної відповіді
1.1.Обчисліть (-2,75)![]() : 2.75
: 2.75![]()
А Б В Г
1 ; 3 ; 2,75 ; -1.
1.2.Скільки коренів має рівняння Х![]() = 0
= 0
А Б В Г
один ; три ; жодного ; безліч.
1.3. Графіком якої функції є парабола
А Б В Г
Y=Х ; Y=Х![]() ; Y=
; Y=![]() ; Y=
; Y=![]() .
.
1.4. Укажіть ірраціональне число
А Б В Г
3,14; -1,7; ![]() ;
; ![]() .
.
2. Завдання з вибором двох правильних відповідей
2.1. Укажіть які твердження є хибними
А порядок числа 3,07·10![]() дорівнює 5;
дорівнює 5;
Б число 0,1·10![]() записано в стандартному вигляді;
записано в стандартному вигляді;
В число 2·10![]() менше від числа 9·10
менше від числа 9·10![]() ;
;
Г швидкість світла становить 3·10![]()
![]() .
.
2.2.Дано функцію Y=Х![]() .Які прямі перетинають графік цієї функції?
.Які прямі перетинають графік цієї функції?
А Б В Г
Y=1; Y=-1; Y=-100; Y=2010.
3.Завдання на встановлення логічної пари
3.1.Квадратне рівняння Вид рівняння Відповідь
А 2Х![]() -7Х-30=0; 1 біквадратне; А- ;
-7Х-30=0; 1 біквадратне; А- ;
Б Х![]() -12Х +7=0; 2 неповне зведене; Б- ;
-12Х +7=0; 2 неповне зведене; Б- ;
В Х![]() -25=0; 3 повне незведене; В- ;
-25=0; 3 повне незведене; В- ;
Г Х![]() -5Х
-5Х![]() + 4=0; 4 повне зведене; Г- .
+ 4=0; 4 повне зведене; Г- .
3.2.Квадратне рівняння Характеристика Відповідь
А Х![]() - 4Х + 12=0; 1 сума коренів -12; А- ;
- 4Х + 12=0; 1 сума коренів -12; А- ;
Б Z![]() + 4Z + 12=0; 2 сума коренів 4; Б- ;
+ 4Z + 12=0; 2 сума коренів 4; Б- ;
В Y![]() + Y -12=0; 3 сума коренів -4; В- ;
+ Y -12=0; 3 сума коренів -4; В- ;
Г Х![]() + 12Х -20=0; 4 добуток коренів -12; Г- .
+ 12Х -20=0; 4 добуток коренів -12; Г- .
4.Завдання на встановлення правильної послідовності
4.1. Визначте послідовність значень виразів у порядку спадання .
А Б В Г
![]() ·
·![]() ; 1-
; 1-![]() ; 8,3·10
; 8,3·10![]() ;
; ![]() .
.
Відповідь 1- ; 2- ; 3- ; 4- .
4.2.Визначте послідовність значень виразів у порядку зростання
А Б В Г
0,32![]() ;
; ![]() ; 0,32
; 0,32![]() ; 0,32
; 0,32![]() .
.
Відповідь 1- ; 2- ; 3- ; 4- .
5. Завдання з відкритою формою відповіді
5.1.Три трактори мають зорати поле за 48 год. За скільки годин зорють це поле чотири
таких самих трактори?
5.2.До розчину, що містить 40 г солі, додали 200 г води, після чого концентрація зменшилась на 10%. Скільки води містив розчин і яка була його концентрація?
Варіант 2
1.Завдання з вибором однієї правильної відповіді
1.1.Знайдіть частку (-8,75)![]() :(-8,75)
:(-8,75)![]()
А Б В Г
8,75 ; -1 ; -8,75 ; 1.
1.2.Скільки коренів має рівняння Х![]() =0
=0
А Б В Г
три; жодного; безліч; один.
1.3.Графіком функції Y=![]() є
є
А Б В Г
парабола; гіпербола; пряма; кубічна парабола.
1.4.Укажіть, яке число є ірраціональним
А Б В Г
![]() ; -1,5; 3.14:
; -1,5; 3.14: ![]() .
.
2.Завдання з вибором двох правильних відповідей
2.1.Укажіть, які твердження є правильними
А число 32,4·10![]() записано у стандартному вигляді;
записано у стандартному вигляді;
Б порядок числа 5,9·10![]() дорівнює 8;
дорівнює 8;
В число 8·10![]() більше числа 2·10
більше числа 2·10![]() ;
;
Г перша космічна швидкість дорівнює 7,9·10![]()
![]() .
.
2.2.Дано функцію Y=-Х![]() .Які прямі перетинають графік цієї функції?
.Які прямі перетинають графік цієї функції?
А Б В Г
Y=1; Y=-1; Y=-2010; Y=100.
3.Завдання на встановлення логічної пари
3.1. Квадратне рівняння Тип рівняння Відповідь
А 2Х![]() - 50=0; 1 повне незведене; А- ;
- 50=0; 1 повне незведене; А- ;
Б Х![]() -12Х-28=0; 2 неповне зведене; Б- ;
-12Х-28=0; 2 неповне зведене; Б- ;
В Z![]() -64=0; 3 неповне незведене; В- ;
-64=0; 3 неповне незведене; В- ;
Г 3Y![]() +8Y-5=0; 4 повне зведене; Г- .
+8Y-5=0; 4 повне зведене; Г- .
3.2. Квадратне рівняння Характеристика Відповідь
А Х![]() -7Х-18=0; 1 сума коренів -7; А- ;
-7Х-18=0; 1 сума коренів -7; А- ;
Б Х![]() -11Х +18=0; 2 добуток коренів 11; Б- ;
-11Х +18=0; 2 добуток коренів 11; Б- ;
В Z![]() +7Z -18=0; 3 сума коренів 7; В- ;
+7Z -18=0; 3 сума коренів 7; В- ;
Г Y![]() +12Y +11=0; 4 добуток коренів 18; Г- .
+12Y +11=0; 4 добуток коренів 18; Г- .
4.Завдання на встановлення правильної послідовності
4.1.Визначте послідовність значень виразів у порядку зростання
А Б В Г
![]() ·
·![]() ; 1-
; 1-![]() ; 7,4·10
; 7,4·10![]() ;
; ![]() .
.
Відповідь: 1- ; 2- ; 3- ; 4- .
4.2.Визначте послідовність значень виразів у порядку спадання
А Б В Г
0,74![]() ;
; ![]() ; 0,74
; 0,74![]() ; 0,74
; 0,74![]() .
.
Відповідь: 1- ; 2- ; 3- ; 4- .
5. Завдання з відкритою формою відповіді
5.1.Чотири трактори мають зорати поле за 36 год. За скільки годин зорють це поле три
таких самих трактори?
5.2.До 20%-го розчину кислоти додали 200 г води, після чого його концентрація зменшилась на 10%.Якою стала концентрація розчину і скільки в ньому води?
Тема№1: Нерівності та їх властивості. Лінійні нерівності з однією змінною
Математичний диктант
Нерівності. Поняття числових нерівностей.
- За допомогою яких знаків записують строгі нерівності?
- Порівняйте числа 5 і -3.
- Використовуючи числа 2 і -3, запишіть нерівність із знаком «<».
- Якою буде різниця чисел а і в, якщо відомо, що а>в.
- Порівняйте числа а і в, якщо а-в=-2,5.
- Позначте на координатній прямій числа а, в, с, якщо а>в і с>а.
- Який знак числа а, якщо 5а<3а?
-
Порівняйте числа
 і 0,3.
і 0,3.
- Доведіть нерівність 4+в2≥4в.
Властивості числових нерівностей
- Продовжіть речення: 2>-3, то…
- Якщо -3<2 і 2<5, то…
- Якщо а>3, в>5, то а + в…
- Якщо а>3, то а + 2…
- Оцініть вираз -2а, якщо а>5.
- Оцініть вираз ав, якщо а>2, в>5.
- Оцініть вираз -5х, якщо -2<х<3.
- Оцініть вираз ху, якщо 5<х<8 , 2<у<3.
-
Оцініть вираз
 , якщо 4<х<6.
, якщо 4<х<6.
Числові проміжки
Зобразіть на координатній прямій множину чисел,
що задовольняють дані нерівності:
- х>2.
- х<-3.
- х≥5.
- х≤0.
- 2<х<5.
- 2≤х<5.
- -2<х≤3.
- -4≤х≤3.
- |х|≤5.
Рівносильні нерівності
Встановіть істинність тверджень
- Якщо а>в, то 2а>2в.
- Якщо а<в, то а+1>в+1.
- Якщо а>в, то -3а<-3в.
- Якщо а>в, то -4а>-4в.
- Якщо х>у, то 2х-3>2у-3.
-
Якщо а>в, то
 >
> .
.
-
Якщо а>в, то
 +1 <
+1 <  +1.
+1.
-
Якщо х>у, то 3 -
 >3-
>3-  .
.
- Якщо х>у, то -х>-у.
Числові нерівності та їх властивості
2 бали. 1.Відомо, що а > b. Порівняти і записати у вигляді нерівності
а) – 12а і –12b;
б) 2,5а і 2,5b;
в) 0,1а і 0,1 b.
2 бали. 2. Запишіть нерівність, яку отримаємо:
а) якщо до обох частин нерівності -1 < 3 додати число 4,5; число -2.
б) якщо обидві частини нерівності помножити на число 8; число -5.
в) якщо обидві частини нерівності 9 < 27 розділимо на 3; на -1.
2 бали. 3. Який знак числа а, якщо відомо, що:
а) 5а > 3; в) – 6а < 2а;
б) 9а < 5а; г) – 11а > – 4а.
2 бали. 4. Чи вірно, якщо:
а) а > 5 і b > 7, то а + b > 12; а + b > 10; а + b > 15;
б) а > 4 і b > 6, то а b > 24; а b > 20; а b > 22;
в) а < 3 і b < 7, то а b < 21?
2 бали. 5. Чи вірне твердження:
а) Якщо х > 2, то х2 > 4;
б) Якщо х < 2, то х2 < 4;
в) Якщо х > 2, то ![]() <
< ![]() .
.
2 бали. 6. Відомо, що а < b. Поставте замість * знак > або < , щоб
отримати вірну нерівність:
а) а – 4 * b – 4; в) –2,3а * –2,3b;
б) 10,5а * 10,5 b; г) 12 – а * 12 – b;
д) –![]() * –
* –![]() .
.
Самостійна робота
Додавання і множення числових нерівностей
1.Додайте числові нерівності:
3>2 і 5>-4;
-2<5 і -4<-1;
2>-1 і 4<7;
-1<х<3 і -2<у<-1.
2.Перемножте числові нерівності:
2>1,5 і 3>2;
5<8 і 2<2,5;
3<5 і 4>2;
2<х<5 і 7>у>4.
Розв’язування нерівностей з однією змінною.
1.Розв’яжіть нерівності:
2х-1<3;
2х+3![]()
2(х-4)+3х<х+3;
![]() –
– ![]() 2-х.
2-х.
2. Запишіть дві рівносильні нерівності, розв’язками яких є усі числа, більші від п’яти.
Тематична контрольна робота №1
Нерівності та їх властивості.
Лінійні нерівності з однією змінною
Варіант 1
Частина I
- Якщо а-b=2,75, то
|
А |
Б |
В |
Г |
|
а=b |
а>b |
а<b |
а і b порівняти не можна |
- Якщо а<b, то правильною є нерівність
|
А |
Б |
В |
Г |
|
3а<3b |
-3а<-3b |
а+1<b |
а=b |
- Якщо 2,1<а<3,5, то
|
А |
Б |
В |
Г |
|
-2,1<-а<-3,5 |
-2,1≤-а<3,5 |
-3,5<-а<-2,1 |
2,1<-а<-3,5 |
- Якщо а – сторона квадрата, причому а≥5см, то його периметр
|
А |
Б |
В |
Г |
|
Р≥20 см |
Р≥10 см |
Р<20 см |
Р=20 см |
Частина II
- Розв’яжіть нерівність 2х-3≥1-4(х-5).
-
При яких значеннях змінної вираз
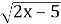 має зміст?
має зміст?
Частина III
- Знайдіть найменший цілий розв’язок нерівності
(х+4)2-2х(х+9)<1-(х+3)(х-3).
Варіант 2
Частина I
- Якщо а-b=-1,23, то
|
А |
Б |
В |
Г |
|
а=b |
а>b |
а<b |
а і b порівняти не можна |
- Якщо а>b, то правильною є нерівність
|
А |
Б |
В |
Г |
|
-2а>-2b |
0,3а>0,3b |
0,2а<0,2b |
а>2b |
- Якщо -1<а<3, то
|
А |
Б |
В |
Г |
|
1<-а<-3 |
-3<-а<-1 |
1>-а>3 |
-1<-а<3 |
- Якщо а – сторона трикутника, причому а≤2 см, то його периметр
|
А |
Б |
В |
Г |
|
Р≤6 см |
Р=4 см |
Р≥6 см |
Р=6 см |
Частина II
- Розв’яжіть нерівність 3х-1≤2-5(х-1).
-
При яких значеннях змінної вираз
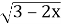 має зміст?
має зміст?
Частина III
- Знайдіть найменший цілий розв’язок нерівності
1-(х-3)(х+3)>(х+4)2-2х(х+9).
Тема№2: Системи лінійних нерівностей з однією змінною
Математичний диктант
Системи лінійних нерівностей з однією змінною
Зобразіть на числовій прямій розв’язки системи нерівностей:
3. ![]()
4. ![]()
5. ![]()
6. ![]()
Запишіть системи нерівностей, розв’язки яких зображені на координатній прямій:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 7.
7.
2 5
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 8.
8.
-2 3
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 9.
9.
-7 -8
Самостійна робота
Варіант 1
1. (2б) Яке число є розв’язком системи нерівностей![]()
А) 1; Б) 30; В)12; Г) 25.
2. (2б) Знайдіть область визначення функції:![]()
![]()
А) (3,5; ![]()
![]()
![]() ; 3,5); Г)
; 3,5); Г)![]() ; 3,5].
; 3,5].
3. (2б) Знайдіть найбільший цілий розв’язок нерівності:
(х - 1) (х + 1) < 2(х -5)2 – х ( х - 3).
4. (2б) При яких значеннях змінної значення виразу ![]() менше значення виразу 2(х - 3)?
менше значення виразу 2(х - 3)?
5. (2б) Розв’яжіть подвійну нерівність та знайдіть середнє арифметичне її цілих розв’язків
-6,5 ≤ ![]() ≤ 20,5.
≤ 20,5.
6. (2б) Знайдіть кількість натуральних розв’язків системи нерівностей
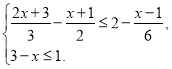
![]()
Варіант 2
1. (2б) Яке число є розв’язком системи нерівностей![]()
А) 3; Б) 4; В)2; Г) -15.
2. (2б) Знайдіть область визначення функції:![]()
![]()
А) (2; ![]()
![]()
![]() ; 2); Г)
; 2); Г)![]() ; 2].
; 2].
3. (2б) Знайдіть найменше ціле число, яке є розв’язком нерівності.
(3х +2)2 - (9х - 1)(х + 1) > 17.
4. (2б) При яких значеннях змінної значення виразу ![]() менше значення виразу
менше значення виразу ![]()
5. (2б) Розв’яжіть подвійну нерівність та знайдіть середнє арифметичне її цілих розв’язків
-2,5 ≤ ![]() ≤ 1,5.
≤ 1,5.
6. (2б) Знайдіть кількість натуральних розв’язків системи нерівностей
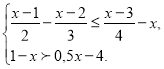
Тематична контрольна робота №2
Системи лінійних нерівностей з однією змінною
Варіант 1
ЧастинаI
-
Розв’язком системи нерівностей
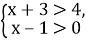 є число
є число
|
А |
Б |
В |
Г |
|
0 |
2 |
-2 |
3 |
- Спільною частиною двох проміжків (-2;0) і (3;5) є проміжок
|
А |
Б |
В |
Г |
|
(-2;3) |
Ø |
(-2;5) |
(0;3) |
-
Виберіть правильний розв’язок системи нерівностей
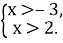
|
А |
Б |
В |
Г |
|
х>2 |
х>-3 |
х>-1 |
0 |
-
При яких значеннях змінної х вираз
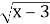 має зміст?
має зміст?
|
А |
Б |
В |
Г |
|
х>3 |
х≥3 |
х>-1 |
х>0 |
Частина II
-
Розв’яжіть систему нерівностей та зобразіть на координатній прямій її розв’язки
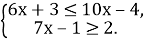
- Значення виразу 2х-5 належить проміжку (-1;3). Оцініть х.
Частина III
7. Знайдіть область визначення функції у=![]() -
- ![]() .
.
Варіант 2
Частина I
-
Розв’язком системи нерівностей
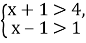 є число
є число
|
А |
Б |
В |
Г |
|
0 |
3 |
2 |
-2 |
- Спільною частиною двох проміжків (-3;1) і (2;4) є проміжок
|
А |
Б |
В |
Г |
|
(-3;4) |
(1;2) |
Ø |
(-3;2) |
-
Розв’язком системи нерівностей
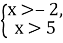 є проміжок
є проміжок
|
А |
Б |
В |
Г |
|
х>0 |
х>5 |
х>-2 |
х>3 |
-
При якому значенні змінної існує вираз
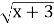 ?
?
|
А |
Б |
В |
Г |
|
х>3 |
х≥-3 |
х>-3 |
х>0 |
Частина II
-
Розв’яжіть систему нерівностей та зобразіть на координатній прямій її розв’язки
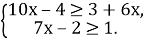
- Значення виразу 3х+2 належить проміжку (-4;1). Оцініть х.
Частина III
-
Знайдіть область визначення функції у=
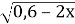 +
+ 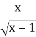 .
.
Тема№3: Функція та її властивості.
Квадратична функція та її графік
Математичний диктант
Квадратична функція
- Що називають функцією?
- Що таке аргумент функції?
- Одному значенню змінної х відповідає два значення змінної у. Чи є така залежність між змінними х та у функцією?
- Двом різним значенням змінної х відповідає єдине значення змінної у. Чи можна вважати таку залежність функцією?
- Знайдіть область визначення функції у=2х-3.
- Знайдіть значення функції у=2х-3 при значенні аргументу, що дорівнює -1.
-
Знайдіть область визначення функції у=
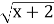 .
.
- У деякій точці х значення функції у=х2-1 дорівнює 3. Знайдіть відповідне значення змінної х.
-
При яких значеннях змінної х існує функція у=
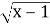 –
– 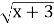 ?
?
Розташування графіка квадратичної функції
в системі координат
Вкажіть координати вершини, напрям віток і шаблон для побудови параболи:
- у=х2=3.
- у=х2-1.
- у=-х2-2.
- у=3-х2.
- у=(х-2)2.
- у=-2(х-3)2.
- у=х2-2х.
- у=3(х-1)2-4.
- у=-0,5(х+3)2+5.
Графічна робота №1
з теми: «Квадратична функція»
-
Побудуйте графік функції
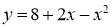 . Користуючись графіком, знайдіть:
. Користуючись графіком, знайдіть:
а) область значення даної функції;
б) при яких значеннях ![]() функція набуває додатних значень.
функція набуває додатних значень.
-
Побудуйте графік функції
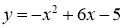 . Користуючись графіком знайдіть:
. Користуючись графіком знайдіть:
а) проміжок спадання функції;
б) при яких значеннях ![]() функція набуває від’ємних значень.
функція набуває від’ємних значень.
- Побудуйте графіки функцій:
1) ![]() ;
;
2) 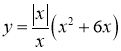 ;
;
3) 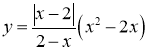 ;
;
4) ![]() ;
;
5) 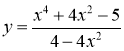 ;
;
6) 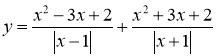 .
.
-
Скільки коренів має рівняння
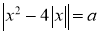 залежно від значення параметра
залежно від значення параметра 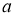 .
.
-
Побудуйте в одній системі координат графіки функцій
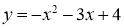 і
і 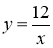 . Встановити, користуючись одержаним малюнком, кількість коренів рівняння
. Встановити, користуючись одержаним малюнком, кількість коренів рівняння 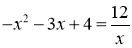 .
.
Графічна робота №2
з теми: «Квадратична функція»
- Побудуйте графік функції:
а) 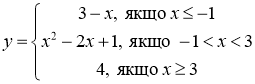 ;
;
б) 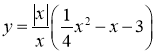 ;
;
в) 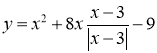 ;
;
г) ![]() ;
;
д) ![]() .
.
-
При яких значеннях
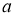 функція
функція 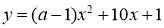 набуває невід’ємних значень при всіх дійсних значеннях
набуває невід’ємних значень при всіх дійсних значеннях 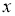 ?
?
- Побудуйте графіки рівняння:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
5) 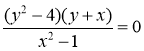 ;
;
6) 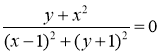 .
.
Самостійна робота
Варіант 1
1. у = х2. Якою формулою (в загальному вигляді) задається функція у = х2 – 5?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
2. Графік функції ![]() проходить через точку М (1;1). Через яку точку проходить графік функції
проходить через точку М (1;1). Через яку точку проходить графік функції ![]() ?
?
|
А |
Б |
В |
Г |
Д |
|
К (1; |
К ( |
К (3; 1) |
К (1; 3) |
К (1 |
3. З-поміж наведених графіків укажіть графік функції ![]() :
:
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
4. Встановіть відповідність між геометричними перетвореннями графіка функції ![]() (1-4) та функціями, одержаними в результаті таких перетворень (А-Д):
(1-4) та функціями, одержаними в результаті таких перетворень (А-Д):
|
1) |
графік функції |
А) |
|
|
2) |
графік функції |
Б) |
|
|
3) |
графік функції |
В) |
|
|
4) |
графік функції |
Г) |
|
|
|
|
Д) |
|
5. Розв’язати графічно рівняння 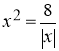 .
.
Варіант 2
1. ![]() . Якою формулою (в загальному вигляді) задається функція
. Якою формулою (в загальному вигляді) задається функція ![]() ?
?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
2. Графік функції ![]() проходить через точку М (1;1). Через яку точку проходить графік функції
проходить через точку М (1;1). Через яку точку проходить графік функції ![]() ?
?
|
А |
Б |
В |
Г |
Д |
|
К (1; –1) |
К (2; 1) |
К (1; 3) |
К (3; 1) |
К (–1; 1) |
3. З-поміж наведених графіків укажіть графік функції ![]() :
:
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
4. Встановіть відповідність між геометричними перетвореннями графіка функції ![]() (1-4) та функціями, одержаними в результаті таких перетворень (А-Д):
(1-4) та функціями, одержаними в результаті таких перетворень (А-Д):
|
1) |
графік функції |
А) |
|
|
2) |
графік функції |
Б) |
|
|
3) |
графік функції |
В) |
|
|
4) |
графік функції |
Г) |
|
|
|
|
Д) |
|
5. Розв’язати графічно рівняння ![]() .
.
Варіант 3
1. ![]() . Якою формулою (в загальному вигляді) задається функція
. Якою формулою (в загальному вигляді) задається функція ![]() ?
?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
2. Графік функції ![]() проходить через точку М (1;1). Через яку точку проходить графік функції
проходить через точку М (1;1). Через яку точку проходить графік функції ![]() ?
?
|
А |
Б |
В |
Г |
Д |
|
К (1; –1) |
К (2; 1) |
К (1; 3) |
К (3; 1) |
К (–1; 1) |
3. З-поміж наведених графіків укажіть графік функції ![]() :
:
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
4. Встановіть відповідність між геометричними перетвореннями графіка функції у = х2 (1-4) та функціями, одержаними в результаті таких перетворень (А-Д):
|
1) |
графік функції у = х2 паралельно перенесли вздовж осі ОY на 1 одиницю вгору; |
А) |
у = (х – 1)2 |
|
2) |
графік функції у = х2 паралельно перенесли вздовж осі ОХ на 1 одиницю вліво; |
Б) |
у = х2 – 1 |
|
3) |
графік функції у = х2 паралельно перенесли вздовж осі ОY на 1 одиницю вниз; |
В) |
у = (х + 1)2 |
|
4) |
графік функції у = х2 паралельно перенесли вздовж осі ОХ на 1 одиницю вправо; |
Г) |
у = (х – 1)2 + 1 |
|
|
|
Д) |
у = х2 + 1 |
5. Розв’язати графічно рівняння ![]() .
.
Варіант 4
1. ![]() . Якою формулою (в загальному вигляді) задається функція
. Якою формулою (в загальному вигляді) задається функція![]() ?
?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
2. Графік функції ![]() проходить через точку М (1;1). Через яку точку проходить графік функції
проходить через точку М (1;1). Через яку точку проходить графік функції ![]() ?
?
|
А |
Б |
В |
Г |
Д |
|
К (1; |
К ( |
К (3; 1) |
К (1; 3) |
К (1 |
3. З-поміж наведених графіків укажіть графік функції ![]() :
:
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
4. Встановіть відповідність між геометричними перетвореннями графіка функції у = х2 (1-4) та функціями, одержаними в результаті таких перетворень (А-Д):
|
1) |
графік функції у = х2 стиснули у 4 рази до осі ОY; |
А) |
|
|
2) |
графік функції у = х2 розтягнули у 4 рази від осі ОY; |
Б) |
|
|
3) |
графік функції у = х2 стиснули у 4 рази до осі ОХ; |
В) |
|
|
4) |
графік функції у = х2 розтягнули у 4 рази від осі ОХ. |
Г) |
|
|
|
|
Д) |
|
5. Розв’язати графічно рівняння ![]() .
.
Тематична контрольна робота №3
Функція та її властивості.
Квадратична функція та її графік
Варіант 1
Частина I
- Функція задана формулою у=2х-3. В точці х=-2 значення функції дорівнює
|
А |
Б |
В |
Г |
|
-7 |
7 |
1 |
0 |
- Яка із вказаних точок належить графіку функції у=2х-3?
|
А |
Б |
В |
Г |
|
(1;-1) |
(1;1) |
(1;5) |
(0;1) |
- Вершина параболи у=х2+2 знаходиться в точці
|
А |
Б |
В |
Г |
|
(0;-2) |
(0;2) |
(2;2) |
(0;0) |
- Функція у=х2 зростає на проміжку
|
А |
Б |
В |
Г |
|
(0;2) |
[0; |
(- |
(0;3) |
Частина II
- Побудуйте графік функції у=х2+3. Укажіть проміжки зростання і спадання.
- Знайдіть нулі функції у=х2-2х та вкажіть проміжки знакосталості.
Частина III
- Побудуйте графік функції у=х2-6х+5.
Вкажіть координати вершини параболи, проміжки зростання і спадання функції.
Варіант 2
Частина I
- Функція задана формулою у=3х-2. В точці х=-2 значення функції дорівнює
|
А |
Б |
В |
Г |
|
4 |
-8 |
8 |
0 |
- Яка із вказаних точок належить графіку функції у=2х+3?
|
А |
Б |
В |
Г |
|
(0;1) |
(1;5) |
(1;-1) |
(2;3) |
- Вершина параболи у=х2-3 знаходиться в точці
|
А |
Б |
В |
Г |
|
(0;3) |
(0;-3) |
(9;3) |
(0;0) |
- Функція у=х2 спадає на проміжку
|
А |
Б |
В |
Г |
|
(0;5) |
(- |
(-3;2) |
(-2;0) |
Частина II
5. Побудуйте графік функції у=х2-4. Укажіть проміжки зростання і спадання.
6. Знайдіть нулі функції у=4х-х2 та вкажіть проміжки знакосталості.
Частина III
- Побудуйте графік функції у=х2-3х+2.
Вкажіть координати вершини параболи, проміжки зростання і спадання функції.
Підсумкова контрольна робота за І семестр з алгебри
у 9-х класах
Варіант 1
І частина (5 балів)
№1. Додати нерівності 0,18 < 8 і 0,2 < 6 .
А) 0,38 < 14; Б) 0,28 < 14; В) 0,2 < 14; Г) 0,36 < 48 .
№2. Який з проміжків є розв’язком нерівності ![]() ≥ 48 ?
≥ 48 ?
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
№3. Знайти область визначення функції ![]() :
:
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
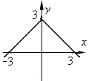
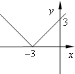
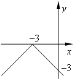
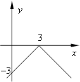
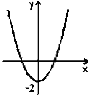
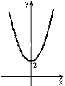
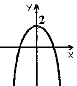
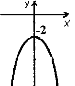
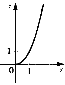
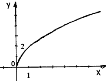
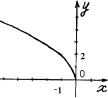
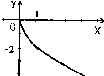
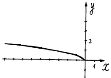
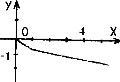
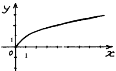
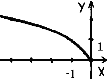
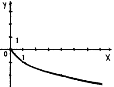
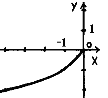
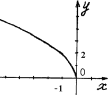
№4. На якому з малюнків зображено графік функції ![]() ?
?
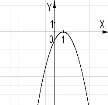
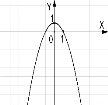
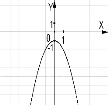
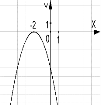 А) Б) В) Г)
А) Б) В) Г)
№5. Вкажіть, в якій чверті розташована вершина параболи
у = х2 + 6х + 8?
А) I; Б) IІ; В) IІI; Г) IV.
ІІ частина (4 бали)
№6. Знайти найбільший цілий розв’язок нерівності
![]() < 3 .
< 3 .
№7. Оцінити периметр рівнобічного трикутника з основою а см та бічною стороною b см, якщо 30 < а <50; 10 < b < 40.
ІІІ частина (3 бали)
№8. Розв’язати систему нерівностей : 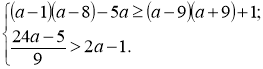
Варіант 2
І частина (5 балів)
№1. Знайти добуток нерівностей 0,5 < 6 і 8 < 15 .
А) 4 < 21; Б) 4 < 90; В) 40 < 90; Г) 8,5 < 21.
№2. Який з проміжків є розв’язком нерівності ![]() ?
?
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
№3. Знайти область визначення функції ![]() :
:
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
№4. На якому з малюнків зображено графік функції ![]() ?
?
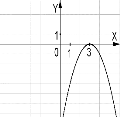
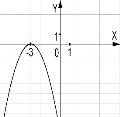
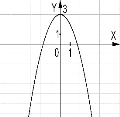
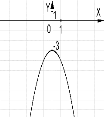 А) Б) В) Г)
А) Б) В) Г)
№5. Вкажіть, в якій чверті розташована вершина параболи у = х2 – 2х – 8 ?
А) I; Б) IІ; В) IІI; Г) IV.
ІІ частина (4 бали)
№6. Знайти найбільший цілий розв’язок нерівності
![]() > 1 .
> 1 .
№7. Оцінити середню лінію трапеції з основами х см та у см, якщо
9 < х < 13; 8 < у < 15.
ІІІ частина (3 бали)
№8. Розв’язати систему нерівностей : 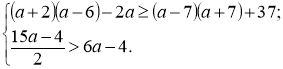
Тема№4: Нерівності другого степеня з однією змінною.Розв’язування нерівностей методом інтервалів.Системи рівнянь з двома змінними
Математичний диктант
Системи рівнянь другого степеня з двома змінними
1 бал. 1. Вказати, які способи розв’язування систем рівнянь ви знаєте.
![]() 1 бал. 2. У даній системі рівнянь вказати графік кожного рівняння.
1 бал. 2. У даній системі рівнянь вказати графік кожного рівняння.
x 2 + y 2 = 25;
x y = 12.
![]() 2 бали. 3. Чи є розв’язком системи x 2 + y 2 = 1; пара чисел:
2 бали. 3. Чи є розв’язком системи x 2 + y 2 = 1; пара чисел:
x + y = 1
|
а) (1; 0) |
б) (– 1; 0) |
в) (0; – 1) |
г) (0; 1)? |
4. Запишіть систему рівнянь за умовою задачі, позначивши через x і y невідомі величини.
2 бали. а) Знайдіть катети прямокутного трикутника, якщо його гіпотенуза дорівнює 13 см, а периметр 30 см.
2 бали. б)Знайдіть два числа, якщо їхня сума дорівнює 7 см, а їхній добуток – 10.
2 бали. в) Знайдіть два числа, якщо сума цих чисел в 5 разів більша за їхню різницю, а різниця їхніх квадратів дорівнює 180.
2 бали. г) Знайдіть сторони прямокутника, якщо його діагональ дорівнює 13 см, а площа 6 см.
Самостійна робота
Варіант 1
1.(1б) Визначте степінь рівняння: 2х3 ![]()
А)![]()
![]()
![]()
2. (1б) Яка пара чисел є розв’язком системи рівнянь 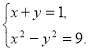
А) (-3; 4); Б) (5; - 4); В) (4; 3); Г) (- 5;4) ?
3. (1б) Розв’яжіть систему рівнянь: 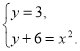
А) (-3; 3); Б) (- 3; 3), (3; 3); В) (3; 3); Г) (3; 3), (0; 3).
4. (2б) Розв’яжіть систему рівнянь: 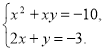
У відповіді вкажіть значення виразу![]() де (х; у) –
де (х; у) –
один із розв’язків системи.
5. (2б) Знайдіть значення виразу 5а2 – b2, якщо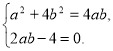
6. (2б) Розв’яжіть задачу складанням системи рівнянь.
Периметр прямокутника дорівнює 20 см, а сума площ квадратів, побудованих на всіх його сторонах, дорівнює 104 см2. Знайдіть
сторони прямокутника.
7. (3б) Розв’яжіть графічно систему рівнянь: 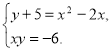
У відповіді вкажіть найменше значення виразу у - х,
де (х; у) – один із розв’язків системи.
Варіант 2
1. (1б) Визначте степінь рівняння: ![]()
А)![]()
![]()
![]()
2. (1б) Яка пара чисел є розв’язком системи рівнянь 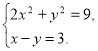
А) (4; 1); Б) (0; -3); В) (-3; 0); Г) (0; 3) ?
3. (1б) Розв’яжіть систему рівнянь: 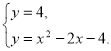
А) (-4; 4); Б) (- 3; 4); В) (4; 4), (-2; 4); Г) (2; 4).
4. (2б) Розв’яжіть систему рівнянь: 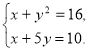
У відповіді вкажіть значення виразу![]() де (х; у) – один із
де (х; у) – один із
розв’язків системи.
5. (2б) Знайдіть значення виразу 3а2 – b2, якщо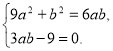
6. (2б) Розв’яжіть задачу складанням системи рівнянь.
Площа прямокутника дорівнює 12 см2, а довжина його діагоналі дорівнює 5 см. Знайдіть сторони прямокутника.
7. (3б) Розв’яжіть графічно систему рівнянь: 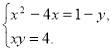
У відповіді вкажіть найменше значення виразу х - у,
де (х; у) – один із розв’язків системи.
Тематична контрольна робота №4
Нерівності другого степеня з однією змінною
Розв’язування нерівностей методом інтервалів
Системи рівнянь з двома змінними
Варіант 1
Частина I
- Графік функції у=8х+х2 перетинає вісь абсцис у точках
|
А |
Б |
В |
Г |
|
(0;8), (0;0) |
(0;0), (-8;0) |
(8;0), (7;0) |
(8;8) |
- Функція у=х2-4 має нулі в точках з абсцисою
|
А |
Б |
В |
Г |
|
-2 і 2 |
2 і 0 |
-2 і 3 |
0 і -2 |
-
Розв’язком системи рівнянь
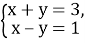 є пара чисел
є пара чисел
|
А |
Б |
В |
Г |
|
(1;2) |
(2;1) |
(0;1) |
(3;1) |
- Розв’язком нерівності (х+1)(х-2)<0 є проміжок
|
А |
Б |
В |
Г |
|
(1;4) |
(-1;2) |
(1;2] |
[0;2) |
Частина II
- Знайти суму цілих розв’язків нерівності -2х2+7х-5≥0.
- Розв’язати нерівність (х2-9)(х+2)>0 методом інтервалів.
Частина III
7. Перший насос перекачує 90м3 води на одну годину швидше, ніж другий 100м3 води. Скільки води щогодини прекачує кожен насос, якщо перший перекачує за одну годину на 5м3 води більше, ніж другий?
Варіант 2
Частина I
1. Графік функції у=6х+х2 перетинає вісь абсцис у точках
|
А |
Б |
В |
Г |
|
(0;8), (0;0) |
(0;6), (0;0) |
(-6;0), (0;0) |
(6;0) |
2. Функція у=х2-9 має нулі в точках з абсцисою
|
А |
Б |
В |
Г |
|
-2 і 0 |
3 і 0 |
-3 і 3 |
0 і -3 |
3. Розв’язком системи рівнянь ![]() є пара чисел
є пара чисел
|
А |
Б |
В |
Г |
|
(4;1) |
(1;4) |
(4;4) |
(0;4) |
4. Розв’язком нерівності (х+2)(х-3)<0 є проміжок
|
А |
Б |
В |
Г |
|
(2;3) |
(-2;3) |
(3;0] |
[0;2) |
Частина II
5. Знайти суму цілих розв’язків нерівності 2х2-7х+5≤0.
6. Розв’язати нерівність (х2-4)(х+3)<0 методом інтервалів.
Частина III
- Один робітник виготовляє 96 деталей на 2 години швидше, ніж другий 112 деталей. Скільки деталей виготовляє щогодини кожний робітник, якщо перший робить за годину на 2 деталі більше, ніж другий?
Тема№5: Елементи прикладної математики
Математичний диктант
Елементи прикладної математики
- Округліть до цілих чисел число 12,35.
- Округліть до десятих число 0,27.
-
Запишіть у вигляді подвійної нерівності вираз х=1,2
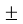
- Вміст цукру у яблуках дорівнює 12%. Скільки цукру міститься у 80кг яблук?
-
Відомо, що
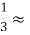 0,3. Знайдіть абсолютну похибку даного наближення.
0,3. Знайдіть абсолютну похибку даного наближення.
- У шухляді лежать 5 різнокольорових олівців: жовтий, зелений, синій, червоний, чорний. Яка ймовірність того, що навмання витягнутий олівець буде синього кольору?
- У шафі лежать пронумеровані папки від 1 до 36. Яка ймовірність того, що номер навмання вибраної папки буде кратним числу 5?
- Вкладник поклав у банк 5000 грн. під 10% річних.Яку суму він одержить через 3 роки?
- До 200г чаю, у якому було 10г цукру, долили 50г води. Який відсотковий вміст цукру був спочатку і яким став після доливання води?
Самостійна робота
Відсоткові розрахунки
- Знайти 12% від 20.
- Знайти число, 15% якого дорівнює 30.
- Цукровий буряк містить 17% цукру. Скільки цукру отримають з 200 ц буряка?
- Скільки грамів цукру треба взяти, щоб приготувати 15%-ний розчин, маючи 170г води?
- Один із заводів випустив за рік на 350 машин більше, ніж другий. Скільки машин випустив кожен завод, якщо 20% машин, випущених першим заводом, на 170 машин менше від 40% машин, випущених другим заводом?
Прості і складні відсотки
- За несвоєчасну сплату боргу нараховується 3% пені за кожен день несплати. Боржник повинен був сплатити 200грн. боргу 5 днів тому. Яку суму він повинен сплатити зараз?
- Комп’ютер коштує 5 тисяч гривень. Щороку на його амортизацію припадає 10% від попередньої вартості. Якою буде ціна комп’ютера через 6 років?
- Вкладник поклав у банк 20 000 гривень під 12% річних. Який прибуток матиме вкладник через 3 роки?
Випадкові події. Ймовірність випадкової події
- Кидають гральний кубик, на кожній з граней якого записане число від 1 до 6. Яка ймовірність того, що внаслідок одного підкидання випаде число 6?
- Випаде число, кратне 3?
- Випаде непарне число?
- У кошику лежать 7 яблук і 5 груш. Яка ймовірність того, що навмання вибраний плід буде яблуко?
- У партії з 20 лампочок 5% бракованих. Яка ймовірність того, що навмання вибрана лампочка не бракована?
Елементи статистики
1.У класі виміряли зріст хлопчиків і отримали такі результати: 158 см, 163 см, 154 см, 170 см, 163 см, 162 см, 161 см, 158 см, 163 см, 162см. Побудуйте ранжований ряд даних вимірювань. Визначте середнє значення зросту хлопчиків у класі.
- При написанні диктанту одну помилку допустили 2 учні, 2 помилки – 5 учнів, 3 помилки – 7 учнів, 4 помилки – 1 учень, 5 помилок – 3 учнів, 6 помилок – 7 учнів. Побудуйте полігон частот одержаних даних. Яка середня кількість помилок припадає на кожного учня?
Тематична контрольна робота №5
Елементи прикладної математики
Варіант 1
Частина I
- Правильно виконано округлення числа 2,195 до десятих
|
А |
Б |
В |
Г |
|
2,1 |
2,2 |
2,20 |
2 |
- Вміст олії в соняшнику 28%. Скільки олії вийде із 200 кг соняшнику?
|
А |
Б |
В |
Г |
|
28 кг |
56 кг |
14 кг |
42 кг |
- Гральний кубик підкинули і на верхній його грані випало якесь число. Яка ймовірність того, що це число – парне?
|
А |
Б |
В |
Г |
|
|
|
|
1 |
- Дано вибірку 2; 1; 1; 3; 5; 2; 1; 1; 1; 5. Яка її мода?
Частина II
- Яка ймовірність того, що навмання вибране двоцифрове число не є квадратом цілого числа?
- Вкладник поклав до банку 5 000 грн. під 15% річних. Яку суму він одержить через 6 років?
Частина III
- Друкуючи щодня на 3 аркуші більше, ніж планувалося, друкарка закінчила роботу обсягом 60 аркушів на 1 день раніше строку. Скільки аркушів планувалося друкувати щодня?
Варіант 2
Частина I
- Правильно виконано округлення числа 3,072 до десятих
|
А |
Б |
В |
Г |
|
3 |
3,1 |
3,07 |
3,0 |
- Вміст цукру в буряках 17%. Скільки цукру вийде із 200 кг буряка?
|
А |
Б |
В |
Г |
|
17 кг |
170 кг |
34 кг |
8,5 кг |
- Гральний кубик підкинули і на верхній його грані випало якесь число. Яка ймовірність того, що це число – непарне?
|
А |
Б |
В |
Г |
|
|
|
|
1 |
- Дано вибірку 2; 1; 1; 3; 5; 2; 1; 1; 1; 5. Яке її середнє значення?
Частина II
- Яка ймовірність того, що навмання вибране двоцифрове число є квадратом цілого числа?
- Вкладник поклав 12 000 гривень під 10% річних. Яку суму він одержить через 4 роки?
Частина III
- Тракторист має зорати поле площею 200 га. Кожен день він орав на 5 га більше, ніж планував, а тому закінчив оранку на 2 дні раніше строку. За скільки днів тракторист зорав поле?
Тема№6 :Числові послідовності.Арифметична і геометрична прогресії
Математичний диктант
Числові послідовності
Поняття послідовності
- Запишіть послідовність, яку утворюють шість перших непарних послідовних чисел.
- Запишіть послідовність, перший член якої дорівнює 2, а кожен наступний на 3 більший від попереднього.
- Запишіть послідовність чисел, перший член якої 8, а кожен наступний удвічі менший.
- Запишіть послідовність чисел, перший член якої 2, другий 3, а кожен наступний дорівнює сумі двох попередніх.
- Відомо, що п’ятий член деякої послідовності дорівнює 10, а кожен наступний на 2 менший від попереднього. Чому дорівнює третій член цієї послідовності?
- Запишіть перших п’ять натуральних членів послідовності, кожен з яких кратний шести.
- Продовжте ряд послідовних чисел 4,8,16,32…
- За яким законом записані числа 1,4,9,16,25…?
- Запишіть формулу n-го члена такої послідовності 5,7,9,11,13…
Арифметична прогресія
аn –арифметична прогресія
- Запишіть 5 перших членів арифметичної прогресії, якщо перший її член дорівнює 3, а різниця 2.
- Запишіть 5 перших членів арифметичної прогресії, якщо а1=6, d=-1.
- Знайдіть різницю арифметичної прогресії, якщо а4=8, а5=6.
- Знайдіть перший член арифметичної прогресії, якщо а2=6, d=4.
- Запишіть формулу n-го члена арифметичної прогресії.
- Знайдіть а8, якщо а1=4, d=2.
- Відомо, що а1=12, а8=20. Знайдіть суму восьми перших членів цієї послідовності.
- Знайдіть суму натуральних чисел від 23 до 30 включно.
- а3=8, а5=14. Знайдіть перший член і різницю арифметичної прогресії.
Геометрична прогресія
bn - геометрична прогресія
- Продовжте ряд чисел 1,3,9,…
- Визначте знаменник геометричної прогресії, якщо b5=18, b6=36.
-
Знайдіть перший член геометричної прогресії, якщо b2=4, q=
 .
.
- Запишіть формулу n-го члена геометричної прогресії.
- Знайдіть b3, якщо b1=5, q=2.
- Знайдіть суму шести перших членів геометричної прогресії, якщо b1=3, q=2.
-
Знайдіть суму нескінченної геометричної прогресії
 ,
,  ,
,  ,
,  ,…
,…
- Знайдіть перший член геометричної прогресії, якщо q=2, b5=80.
- Знайдіть знаменник геометричної прогресії, якщо b1=3, b5=48.
Арифметична прогресія
1 бал. 1. Числовою послідовністю називається…
1 бал. 2. Наведіть приклад нескінченної числової послідовності.
1 бал. 3. Наведіть приклад скінченної числової послідовності.
1 бал. 4. Послідовність задана формулою аn =![]()
Знайдіть а10; а100; а1000.
1 бал. 5. Арифметичною прогресією називається…
1 бал. 6. Формула загального члена арифметичної прогресії аn =…
1 бал. 7. Чи є послідовність арифметичною прогресією?
а) 3; 5; 7; 10; …
б) - 12; - 6; 0; 6; …
1 бал. 8. Знайдіть n – й член арифметичної прогресії
а) 8; 6,5; 5; …
б) 2; 5; 8; …
2 бали. 9. Формула суми членів арифметичної прогресії має вигляд:
Sn = ![]() або Sn =
або Sn = ![]() .
.
2 бали. 10. Знайдіть суму перших семи членів арифметичної
прогресії (аn), якщо а1= - 15; d = 5.
Геометрична прогресія
1 бал. 1. Закінчити твердження:
Числова послідовність, у якій перший член відмінний від нуля, а кожний наступний член …
1 бал. 2. Записати формулу n – го члена геометричної прогресії
1 бал. 3. Скільки членів містить геометрична прогресія 1; 2; 4; …; 128?
1 бал. 4. Запишіть формулу суми n перших членів геометричної прогресії.
2 бали. 5. Чи є дана послідовність геометричною прогресією
а) 20; 10; 0; -10…
б) 2; 8; 16; 32;…
в) 76; 38; 19; 9,5; ..
2 бали. 6. Запишіть формулу для знаходження суми n перших членів геометричної прогресії 1; 2; 4; …; 128
2 бали. 7. Знайдіть суму перших 4 членів геометричної прогресії ( вn), якщо в1=2; q=3.
2 бали. 8. Знайдіть перший член і знаменник геометричної прогресії (вn), якщо в3=6; в6=48.
Самостійна робота
Арифметична прогресія
Самостійна робота №1
- Відомо, що послідовність чисел 2,7,… утворює арифметичну прогресію. Запишіть три наступні члени цієї послідовності.
- Знайдіть різницю арифметичної прогресії, якщо а5=12, а6=10,2.
- Знайдіть шостий член арифметичної прогресії, якщо а5=12, а7=18.
- Знайдіть різницю арифметичної прогресії, якщо її перший член дорівнює 2, а 15-тий – 44.
- Знайдіть перший член і різницю арифметичної прогресії, якщо а7=20, а4=11.
Самостійна робота №2
- Знайдіть суму п’яти перших членів арифметичної прогресії, перший член якої дорівнює 10, а різниця становить -5.
- Знайдіть суму одинадцяти перших членів арифметичної прогресії, якщо а1=6, d=2.
- Знайдіть суму усіх натуральних чисел від 23 до 48 включно.
Геометрична прогресія
Самостійна робота №1
- Продовжити до п’яти чисел геометричну прогресію 2; -6; 18;…
- Знайдіть знаменник геометричної прогресії -6; 18;…
- Знайдіть четвертий член геометричної прогресії, перший член якої дорівнює 5, а знаменник - 2.
4. Знайдіть знаменник геометричної прогресії, якщо b1=-3, b6=-6.
Самостійна робота №2
- Знайдіть суму перших шести членів геометричної прогресії, якщо b1=4, q=2.
2. Знайдіть суму нескінченно спадної геометричної прогресії
![]() ,
, ![]() ,
, ![]() ,
, ![]() …
…
3. Запишіть у вигляді звичайного дробу число 0,(6).
4. Знайдіть суму членів геометричної прогресії від третього до восьмого, якщо b1=4, q=2.
Тематична контрольна робота №6
Числові послідовності
Арифметична і геометрична прогресії
Варіант 1
Частина I
- 2; 6; 10;… - арифметична прогресія. Різниця даної прогресії дорівнює
|
А |
Б |
В |
Г |
|
3 |
4 |
2 |
-4 |
- 2; -6;… - геометрична прогресія. Знаменник цієї геометричної прогресії становить
|
А |
Б |
В |
Г |
|
-4 |
-3 |
-8 |
3 |
- Знайдіть третій член послідовності 6;2;…
|
А |
Б |
В |
Г |
|
2 |
-2 |
0 |
4 |
- Сума нескінченної геометричної прогресії 4; 1; 0,25;… дорівнює
|
А |
Б |
В |
Г |
|
5,25 |
5 |
6 |
10,5 |
Частина II
- (аn) – арифметична прогресія. Знайдіть її різницю, якщо а18=-45, а43=130.
- (bn) – геометрична прогресія. Чому дорівнює знаменник геометричної прогресії, якщо b1=2, b4=-54 ?
Частина III
- Знайдіть знаменник і перший член геометричної прогресії, якщо сума третього і п’ятого її членів дорівнює -20, а сума четвертого і шостого членів цієї послідовності дорівнює -40.
Варіант 2
Частина I
- 3; 7; 11;… - арифметична прогресія. Різниця даної прогресії дорівнює
|
А |
Б |
В |
Г |
|
3 |
4 |
2 |
-4 |
- 2; -6;… - геометрична прогресія. Вкажіть наступний член цієї послідовності.
|
А |
Б |
В |
Г |
|
10 |
-10 |
-18 |
18 |
- Знайдіть третій член послідовності 10;4;…
|
А |
Б |
В |
Г |
|
2 |
-2 |
4 |
0 |
- Сума нескінченної геометричної прогресії 8; 4; 2; 1;… дорівнює
|
А |
Б |
В |
Г |
|
15 |
16 |
18 |
20 |
Частина II
- (аn) – арифметична прогресія. Знайдіть її різницю, якщо а13=89, а21=145.
- (bn) – геометрична прогресія. Чому дорівнює знаменник геометричної прогресії, якщо b1=-6, b4=162 ?
Частина III
- Знайдіть знаменник і перший член геометричної прогресії, якщо сума другого і четвертого її членів дорівнює -10, а сума третього і п’ятого членів цієї послідовності дорівнює -20.
Підсумкова контрольна робота за рік
Варіант 1
І частина (5 балів)
№1. Розв'яжіть систему нерівностей ![]()
А) (9;10); Б) (10;+ ∞); В) (– ∞;10); Г) (9;+ ∞).
№2. Знайдіть координати вершини параболи ![]() .
.
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
№3. Із свіжих груш отримують 18% сушених. Скільки взяли свіжих груш, якщо отримали 9 кг сушених?
А) 50 кг; Б) 500 кг; В) 200 кг; Г) 20 кг.
№4. Відриваємо один аркуш у новому відривному календарі високосного року. Яка з наведених подій є вірогідною?
А) на аркуші 1 вересня; Б) на аркуші число, яке менше за 32;
В) на аркуші 31 червня; Г) відірваний аркуш - вихідний день.
№5. Знайдіть медіану вибірки 9; 17; 26; 7; 14.
А) 17; Б) 14,6; В) 14; Г) 7.
ІІ частина (4 бали)
№6. Розв’яжіть систему нерівностей 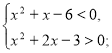 .
.
№7. Знайдіть чотири числа, що утворюють геометричну прогресію, якщо перший член більший від третього на 6, а другий менший від четвертого на 3.
ІІІ частина (3 бали)
№8. Із пункту А до пункту Б, відстань між якими 5 км, вийшов пішохід, а через 30 хв. слідом за ним виїхав велосипедист, швидкість якого на 10 км/год більша від швидкості пішохода. До пункту Б велосипедист приїхав на 10 хв. раніше від пішохода. Знайдіть швидкість велосипедиста і пішохода.
Підсумкова контрольна робота за рік
Варіант 2
І частина (5 балів)
№1. Розв'яжіть систему нерівностей 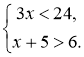
А) (1;8); Б) (8;11); В) (-![]() ;8); Г) (1; +
;8); Г) (1; +![]() ).
).
№2. Знайдіть координати вершини параболи ![]() .
.
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
№3. Із свіжих слив отримують 35% сушених. Скільки сушених слив отримали з 52 кг свіжих?
А) 18 кг; Б) 18,2 кг; В) 1,8 кг; Г) 182 кг.
№4. Відриваємо один аркуш у новому відривному календарі не високосного року.
Яка з наведених подій є неможливою?
А) на аркуші число, яке менше за 32; Б) на аркуші 1 червня;
В) відірваний аркуш - вихідний день; Г) на аркуші 29 лютого.
№5. Знайдіть медіану вибірки 5; 3; 7; 4; 3.
А) 7; Б) 4,5; В) 4; Г) 3.
ІІ частина (4 бали)
№6. Розв’яжіть систему нерівностей 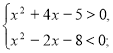
№7. Знайдіть чотири числа, що утворюють геометричну прогресію, якщо відомо, що перше число менше від третього на 36, а друге менше від четвертого на 12.
ІІІ частина (3 бали)
№8. Із пункту А до пункту Б, відстань між якими 10 км., виїхав велосипедист, а через 30 хв. слідом за ним – мотоцикліст, швидкість якого на 30 км/год. більша від швидкості велосипедиста. Знайдіть швидкості велосипедиста і мотоцикліста, якщо до пункту Б мотоцикліст приїхав на 15 хв. раніше від велосипедиста
Література
- Л.М.Адруг, Т.В.Чепурна, «Алгебра 8-10». Моніторинг рівня навчальних досягнень, Харків,2010
- Г.П.Бевз, В.Г.Бевз, «Математика, 8» - К.:Зодіак-ЕКО, 2008
- М.І.Бурда, О.Я.Біляніна, «Збірник завдань для державної підсумкової атестації. Алгебра, 9» - Х.:Гімназія, 2009
- Л.К.Головко, З.В.Дем’яненко «Математика» - К.:Вища школа,1986
- В.Кравчук, В.Підручна, Г.Янченко «Алгебра,9», Тернопіль, 2009
- О.М.Перехейда, Р.П.Ушаков «Доведення нерівностей», Х.:Освіта, 2003
- Т.Г.Роєва, Л.Я.Синельник, С.А.Кононенко «Алгебра у таблицях 7-9»,Х.:Академія, 2001
- З.І.Слєпкань «Збірник завдань для державної підсумкової атестації з алгебри, 9 клас», Х.:Гімназія, 2004.
1


про публікацію авторської розробки
Додати розробку

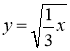
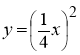
-

Амінова Тетяна Анатоліївна
24.01.2020 в 14:42
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
-

Левитський Михайло Юрійович
27.11.2019 в 13:44
не відкривається, пише помилка
Загальна:
1.0
Структурованість
1.0
Оригінальність викладу
1.0
Відповідність темі
1.0
-

Іваніцька Ірина Станіславівна
21.02.2019 в 11:22
Загальна:
1.7
Структурованість
2.0
Оригінальність викладу
1.0
Відповідність темі
2.0
-

Карпова Лариса Борисівна
06.11.2018 в 15:58
СПАСИБО!
Загальна:
1.0
Структурованість
1.0
Оригінальність викладу
1.0
Відповідність темі
1.0
Показати ще 1 відгук