9-клас.,,Квадратична функція її граіфік та властивості" Презентація.
Про матеріал
В даній презентації показані властивості квадратичної функції,показано графік функції та особливості його побудови,використання основних властивостей для аналізу квадратичної функції.
Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку










![Проміжок,на якому функція зберігає свій знак, називають проміжком знакосталості функції. Проміжки [-4; -2 ), (-2;2,5), (2,5; 4)є проміжками знакосталості функції у = f(x), графік якої зображено на малюнку. Для всiх x ∈(−2;2,5) (див. рис.) виконується умова: графiк лежить вище вiд осi Ox, це означає, що на кожному з цих промiжкiв функцiя набуває додатних значень (y > 0). Для x ∈[−4;−2) ∪ (2,5;4] графiк лежить нижче вiд осi Ox, а отже, на кожному з цих промiжкiв функцiя набуває вiд’ємних значень (y < 0). Проміжок,на якому функція зберігає свій знак, називають проміжком знакосталості функції. Проміжки [-4; -2 ), (-2;2,5), (2,5; 4)є проміжками знакосталості функції у = f(x), графік якої зображено на малюнку. Для всiх x ∈(−2;2,5) (див. рис.) виконується умова: графiк лежить вище вiд осi Ox, це означає, що на кожному з цих промiжкiв функцiя набуває додатних значень (y > 0). Для x ∈[−4;−2) ∪ (2,5;4] графiк лежить нижче вiд осi Ox, а отже, на кожному з цих промiжкiв функцiя набуває вiд’ємних значень (y < 0).](/uploads/files/29885/64304/68772_images/11.jpg)

![2. Зростання функцiїФункцію називають зростаючою на деякому промiжку, якщо бiльшому значенню аргументу з цього промiжку вiдповiдає більше значення функції. Функцiя y = f(x) називається зростаючою на промiжку P, якщо для x1 ∈ P, x2 ∈ P x1 > x2 виконується нерівністьf (x1) < f (x2)Як за графiком знайти промiжки зростання функцiї?Заданий проміжок [ -5; 3]. При x ∈ [−5;−3] i x ∈ [1;3] графiк функцiї y = f(x) «йде» вгору, отже, y = f(x) зростає; 2. Зростання функцiїФункцію називають зростаючою на деякому промiжку, якщо бiльшому значенню аргументу з цього промiжку вiдповiдає більше значення функції. Функцiя y = f(x) називається зростаючою на промiжку P, якщо для x1 ∈ P, x2 ∈ P x1 > x2 виконується нерівністьf (x1) < f (x2)Як за графiком знайти промiжки зростання функцiї?Заданий проміжок [ -5; 3]. При x ∈ [−5;−3] i x ∈ [1;3] графiк функцiї y = f(x) «йде» вгору, отже, y = f(x) зростає;](/uploads/files/29885/64304/68772_images/13.jpg)
![3. Спадання функцiїФункцію називають спадаючою на деякому промiжку, якщо бiльшому значенню аргументу з цього промiжку вiдповiдає менше значення функції. Функцiя y = f(x) називається спадаючою на промiжку P, якщо для x1 ∈ P, x2 ∈ P x1 > x2 виконується нерівністьf (x1) < f (x2)Як за графiком знайти промiжки спадання функцiї?Заданий проміжок [ -5; 3]. При x ∈ [−3;1] графiк функцiї y = f(x) «йде» вниз, отже, y = f(x) спадає. 3. Спадання функцiїФункцію називають спадаючою на деякому промiжку, якщо бiльшому значенню аргументу з цього промiжку вiдповiдає менше значення функції. Функцiя y = f(x) називається спадаючою на промiжку P, якщо для x1 ∈ P, x2 ∈ P x1 > x2 виконується нерівністьf (x1) < f (x2)Як за графiком знайти промiжки спадання функцiї?Заданий проміжок [ -5; 3]. При x ∈ [−3;1] графiк функцiї y = f(x) «йде» вниз, отже, y = f(x) спадає.](/uploads/files/29885/64304/68772_images/14.jpg)
![Приклад. Довести, що функцiя y = x2−1 спадає на промiжку (−∞;0]. Доведення. Нехай x1 i x2 — довiльнi значення аргументу з промiжку (−∞;0], причому x1 < x2. f (x1), f (x2) — вiдповiднi значення функцiї, тобто f (x1) = x12−1, f (x2) = x22−1. Розглянемо рiзницю f (x1)−f (x2) = x12−1−(x22−1) = x12−x22= (x1− x2)(x1+x2). Оскiльки x1 < x2, то x1 − x2 <0. За умовою x ∈ (−∞;0], тому x1 ≤ 0, x2 ≤ 0 i x1+x2 < 0. Отже, (x1−x2)(x1+x2) > 0, тобто f(x1)−f(x2) >0, звiдки дiстанемо, що f(x1) > f(x2), тобто функцiя y = x2−1 на промiжку (−∞;0] спадає. . Приклад. Довести, що функцiя y = x2−1 спадає на промiжку (−∞;0]. Доведення. Нехай x1 i x2 — довiльнi значення аргументу з промiжку (−∞;0], причому x1 < x2. f (x1), f (x2) — вiдповiднi значення функцiї, тобто f (x1) = x12−1, f (x2) = x22−1. Розглянемо рiзницю f (x1)−f (x2) = x12−1−(x22−1) = x12−x22= (x1− x2)(x1+x2). Оскiльки x1 < x2, то x1 − x2 <0. За умовою x ∈ (−∞;0], тому x1 ≤ 0, x2 ≤ 0 i x1+x2 < 0. Отже, (x1−x2)(x1+x2) > 0, тобто f(x1)−f(x2) >0, звiдки дiстанемо, що f(x1) > f(x2), тобто функцiя y = x2−1 на промiжку (−∞;0] спадає. .](/uploads/files/29885/64304/68772_images/15.jpg)
![№ 371. Накресліть схематично графiк функцiї у = g(x), областю визначення якої є промiжок [−3;5], так, щоб : Нулем функції було число 2; нулями функції були числа -1 і 4; функція зростала на проміжку [ -3; 2];Спадала на проміжку [ 2; 5]. № 371. Накресліть схематично графiк функцiї у = g(x), областю визначення якої є промiжок [−3;5], так, щоб : Нулем функції було число 2; нулями функції були числа -1 і 4; функція зростала на проміжку [ -3; 2];Спадала на проміжку [ 2; 5].](/uploads/files/29885/64304/68772_images/16.jpg)

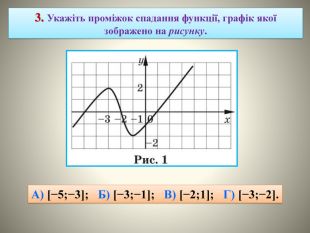
![3. Укажiть промiжок спадання функцiї, графiк якої зображено на рисунку. А) [−5;−3]; Б) [−3;−1]; В) [−2;1]; Г) [−3;−2]. 3. Укажiть промiжок спадання функцiї, графiк якої зображено на рисунку. А) [−5;−3]; Б) [−3;−1]; В) [−2;1]; Г) [−3;−2].](/uploads/files/29885/64304/68772_images/18.jpg)