Контрольні роботи зі стереометрії
Варіант І
1. Запис ![]() означає:
означає:
|
А |
Б |
В |
Г |
Д |
|
Точка М належить прямій α |
Точка М належить площині α |
Точка М не належить площині α |
Точка М не належить прямій α |
Точка М – точка перетину двох прямих |
2. Якщо M, N, F – спільні точки площин α і β, то:
|
A |
Б |
В |
Г |
Д |
|
Точки M, N, F не лежать в одній площині |
|
|
Точки M, N, F лежать на одній прямій |
Точки M, N, F не лежать на одній прямій |
3. Точки X, Y, Z i C не лежать в одній площині. Тоді правильно, що:
|
А |
Б |
В |
Г |
Д |
|
Прямі XY і ZC перетинаються |
Прямі XY і ZC лежать в одній площині |
Прямі XY і YZ не лежать в одній площині |
Прямі XY і YZ не перетинаються |
Прямі XY і ZC не перетинаються |
4.
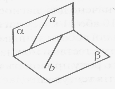
Площини α і β перетинаються. Отже, прямі а і в , зображені на рисунку, …
|
A |
Б |
В |
Г |
Д |
|
Мимобіжні |
Перетинаються |
Паралельні |
Можуть бути по-різному розміщені |
Вірної відповіді немає |
5. Проекції двох різних прямих не можуть:
|
А |
Б |
В |
Г |
Д |
|
Збігатися |
Бути мимобіжними |
Перетинатися |
Бути паралельними |
Всі відповіді вірні |
6. Проекцією ромба не може бути:
|
A |
Б |
В |
Г |
Д |
|
Квадрат |
Паралелограм |
Ромб |
Прямокутник |
Трапеція |
7. Встановіть відповідність між твердженнями (1- 4) та (А – Д):
-
Якщо три точки А, В, С А. АВ
лежать на одній прямій, то через них Б. тільки одну площину
можна провести… В. дві різні площини -
У просторі задано дві прямі Г. BD
а і в які перетинаються в точці О. Д. безліч площин
Через прямі а і в можна провести … -
Чотири точки А, В, С, D не
лежать в одній площині. Площини
АВС і ABD перетинаються
по прямій … -
Точки А, В, С, D не
лежать в одній площині. Площини
АВD і BCD перетинаються
по прямій ….
-
Прямі АС і BD не лежать в одній площині. Доведіть, що прямі АВ і СD не лежать в одній площині.
-
Діагоналі чотирикутника АВСD перетинаються. Доведіть, що всі сторони даного чотирикутника лежать в одній площині.
Варіант ІІ
1.
Якщо β – площина, т – пряма, то правильним є твердження:
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
2. Площини α і β перетинаються по прямій т, точка ![]() . Тоді:
. Тоді:
|
A |
Б |
В |
Г |
Д |
|
|
|
|
|
|
3. Точки M, N і F лежать на одній прямій. Тоді через точки M, N і F:
|
А |
Б |
В |
Г |
Д |
|
Можна провести тільки одну площину |
Можна провести тільки дві різні площини |
Можна провести безліч різних площин |
Не можна провести жодної площини |
Можна провести тільки три різні площини |
4.

Два прямокутники АВСD і AEFD лежать на різних площинах. Прямі ВС і EF:
|
A |
Б |
В |
Г |
Д |
|
Перетинаються |
Паралельні |
Мимобіжні |
Можуть бути розміщені по-різному |
Правильної відповіді немає |
5. Проекцією двох паралельних прямих не може бути:
|
А |
Б |
В |
Г |
Д |
|
Одна пряма |
Одна точка |
Дві прямі |
Дві точки |
Всі відповіді вірні |
6. Проекцією квадрата не може бути:
|
A |
Б |
В |
Г |
Д |
|
Відрізок |
Квадрат |
Ромб |
Прямокутник |
Трапеція |
7. Встановіть відповідності між твердженнями (1 – 4) та (А – Д):
-
Дві прямі, які лежать на одній А. паралельними
площині і не перетинаються, Б. перпендикулярними
називаються … В. мимобіжними -
Дві прямі, які лежать на одній Г. прямими, які перетинаються
площині і перетинаються Д. прямими, які не перетинаю-
під деяким кутом, називають … ся -
Дві прямі, які лежать на одній площині
і перетинаються під прямим кутом,
називаються … -
Дві прямі, які не лежать в одній площині
і не перетинаються, називаються …
- Точки А, В і пряма CD не лежать в одній площині. Доведіть, що прямі АВ і CD не перетинаються.
- Дано пряму а і точку А, що не лежить на цій прямій. Доведіть, що пряма с, яка проходить через точку А і перетинає пряму а, лежить з ними в одній площині.
Відповіді 1
|
Завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
І варіант |
Б |
Г |
Д |
А |
Б |
Д |
1-Д; 2-Б; 3-А; 4-Г |
|
|
|
ІІ варіант |
Г |
В |
В |
Б |
Б |
Д |
1-А; 2-Г; 3-Б; 4-В |
|
|
Відповіді 2
|
Завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
І варіант |
Б |
В |
Б |
А |
В |
Д |
1-В; 2-Г; 3-Д; 4-Б |
8 |
1,2 |
|
ІІ варіант |
В |
В |
Г |
Б |
Г |
А |
1-Б; 2-Г; 3-В; 4-А |
10 |
3 |
Відповіді 3
|
Завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
І варіант |
Г |
B |
Б |
А |
В |
В |
1-В; 2-Б; 3-Д; 4-А |
4 |
30 |
15 |
|
ІІ варіант |
Г |
Б |
Г |
В |
А |
Д |
1-Д; 2-В; 3-Б; 4-Г |
10 |
30 |
6,5 |
Тема: «Паралельність прямих і площин у просторі»
Варіант І
1. Дано паралельні прямі а і в. Скільки існує площин, які проходять через пряму а і паралельні прямій в?
|
А |
Б |
В |
Г |
Д |
|
Жодної |
Одна |
Дві |
Три |
Безліч |
2.

|
A |
Б |
В |
Г |
Д |
|
ABD |
ADD1 |
BDD1 |
A1B1C1 |
АВС |
3. Якщо дана пряма паралельна площині, то …
|
А |
Б |
В |
Г |
Д |
|
Усі прямі площини паралельні даній прямій |
У площині існують прямі, які не паралельні даній прямій |
Кожна пряма площини – мимобіжна з даною прямою |
У площині існують прямі, що перетинають дану пряму |
Відповідь відрізняється від вище-наведених |
4. Якщо дві суміжні сторони паралелограма паралельні площині α, то площина паралелограма і площина α …
|
A |
Б |
В |
Г |
Д |
|
Паралельні |
Перетинаються |
Збігаються чи паралельні |
Мимобіжні |
Паралельні чи перетинаються |
5.

|
А |
Б |
В |
Г |
Д |
|
Паралельні |
Мимобіжні |
Паралельні або мимобіжні |
Перетинаються |
Перетинаються або мимобіжні |
 6.
6.
|
A |
Б |
В |
Г |
Д |
|
Прямі DC i MN перетинаються |
Прямі ВС і ВМ паралельні |
Пряма АВ перетинає площину DCM |
Пряма АВ не належить площині АВМ |
Пряма CD паралельна площині АВМ |
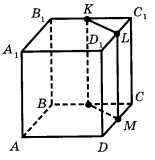
7. На рисунку зображено куб ABCDA1B1C1D1. Установіть відповідність між взаємним розміщенням прямих (1 – 4) та їхніми назвами (А – Д).
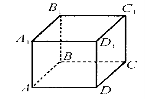
- Паралельні прямі А. ABC i DCC1
- Мимобіжні прямі Б. DCC1 i AB
- Паралельні площини В. AD i B1C1
- Паралельні пряма і площина Г. AD1 i B1C
Д. BB1C1 i ADD1
 8.
8.
9. Дано дві паралельні площини α і β. Точки А і В належать площині α, а точки С і D – площині β. Відрізки AD і BC перетинаються в точці S. Знайдіть довжину відрізка АВ, якщо CD = 3 см, CS = 10 см, BS = 4 см.
- Доведіть, що якщо площина перетинає одну із двох паралельних площин, то вона перетинає і другу.
Варіант ІІ
1. Дано мимобіжні прямі а і в. Скільки існує площин, які проходять через пряму а і паралельні прямій в?
|
А |
Б |
В |
Г |
Д |
|
Дві |
Жодної |
Одна |
Безліч |
Три |
 2.
2.
|
A |
Б |
В |
Г |
Д |
|
АВС |
АВВ1 |
AD1B1 |
А1В1С1 |
ВВ1С1 |
3. Якщо дана пряма паралельна площині, то вона паралельна …
|
А |
Б |
В |
Г |
Д |
|
Усім прямим цієї площини |
Тільки одній прямій цієї площини |
Двом прямим цієї площини, що перетинаються |
Безлічі прямих цієї площини |
Відповідь відрізняється від вище-наведених |
4. Якщо дві суміжні сторони трапеції паралельні площині α, то площина α і площина трапеції …
|
A |
Б |
В |
Г |
Д |
|
Перетинаються |
Паралельні |
Мимобіжні |
Збігаються чи паралельні |
Паралельні чи перетинаються |
5.


|
А |
Б |
В |
Г |
Д |
|
Перетинаються |
Мимобіжні |
Паралельні або мимобіжні |
Перетинаються або мимобіжні |
Паралельні або перетинаються |
6.

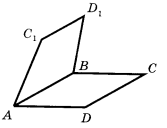
|
A |
Б |
В |
Г |
Д |
|
Пряма АВ паралельна площині C1D1С |
Пряма C1D1 перетинає площину АВС |
Пряма CD перетинає площину АВD1 |
Прямі АВ і ВС - паралельні |
Прямі АD і ВС - мимобіжні |
7. На рисунку зображено куб ABCDA1B1C1D1. Установіть відповідність між взаємним розміщенням прямих (1 – 4) та їхніми назвами (А – Д).
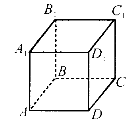
- Паралельні прямі А. AB i DCC1
- Мимобіжні прямі Б. DC1 i AB1
- Паралельні площини В. ADC i A1B1C1
- Паралельні пряма і площина Г. AD i B1C
Д. ABB1 i ADD1
А Б В Г Д
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Розв’яжіть завдання 8 і 9 (з короткою відповіддю).
Відповіді запишіть десятковим дробом у бланку відповідей, дотримуючись правил запису.
 8.
8.

9. Дано дві паралельні площини α і β. Промінь SC перетинає площину α в точці А, а площину β в точці С; промінь SD перетинає площину α в точці В, а площину β в точці D, SA = 7см, SC = 21 см, CD = 9 см. Знайдіть довжину відрізка АВ.
Тема: «Перпендикулярність прямих і площин у просторі»
Варіант І
.
1. Скільки прямих, перпендикулярних даній площині, можна провести через точку поза даною площиною?
|
А |
Б |
В |
Г |
Д |
|
Дві |
Безліч |
Жодної |
Одну |
Три |
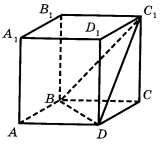
 2.
2.

|
А |
Б |
В |
Г |
Д |
|
DC |
AB |
A1C |
D1C1 |
A1B1 |
3. Якщо μ і η – різні площини, площина μ і пряма п перпендикулярні, площина η і пряма п перпендикулярні, то площини μ і η:
|
А |
Б |
В |
Г |
Д |
|
Перпендику-лярні |
Паралельні |
Перетинаються |
Не паралельні |
Паралельні або перпендикулярні |
4. Скільки площин проходить через дану точку простору перпендикулярно до даної прямої?
|
A |
Б |
В |
Г |
Д |
|
Одна |
Дві |
Три |
Безліч |
Жодної |
5. Проекцією куба при ортогональному проектуванні паралельно його ребру є:
|
А |
Б |
В |
Г |
Д |
|
П’ятикутник |
Прямокутник, що не є квадратом |
Квадрат |
Трикутник |
Шестикутник |
6. Нехай l – довжина відрізка, а l1 – довжина його ортогональної проекції на паралельну площину. Порівняйте l1 і l.
|
A |
Б |
В |
Г |
Д |
|
l1< l |
l< l1 |
l1= l |
Всі варіанти правильні |
Порівняти неможливо |
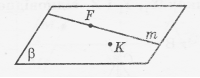
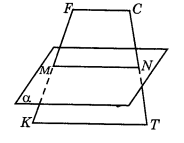
7. Встановіть відповідності, користуючись рисунком:
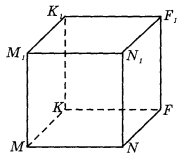
- Паралельними є: А. площини MKF i MNF
- Перпендикулярними є: Б. площини NMM1 i M1K1F1
- Мимобіжними є: В. площини ММ1К1 і NN1F1
- Збігаються: Г. прямі MN i KN
Д. прямі MN i FF1
8. З деякої точки проведена похила, довжина якої дорівнює 5 см і перпендикуляр, довжина якого 3 см. Знайдіть довжину проекції похилої.
9. Через точку О перетину діагоналей прямокутника проведено перпендикуляр КО до площини АВС. Знайти градусну міру кута АКО, якщо АК = АС = 10 см.
Варіант ІІ
.
 1.
1.
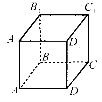
|
А |
Б |
В |
Г |
Д |
|
AD1 |
AC |
AC1 |
AD |
DC |
2. Пряма, яка лежить в одній з двох перпендикулярних площин, перпендикулярна до лінії їх перетину. Як розміщена ця пряма відносно другої площини?
|
A |
Б |
В |
Г |
Д |
|
Паралельна площині |
Перпендикулярна до площини |
Лежить у площині |
Суміщається з площиною |
Мимобіжна площині |
3. Пряма т перпендикулярна до площини α, а пряма п паралельна прямій т. Тоді:
|
А |
Б |
В |
Г |
Д |
|
|
п і α не паралельні |
п і α паралельні або перетинаються |
|
n||α |
4. Дано точка М і площина α. Через точку М до площини α:
|
A |
Б |
В |
Г |
Д |
|
Можна провести одну перпендику-лярну площину |
Можна провести дві різні перпендику-лярні площини |
Можна провести безліч різних перпендику-лярних площин |
Не можна провести жодної перпендику-лярної площини |
Правильної відповіді немає |
5. Проекцією куба при ортогональному проектуванні паралельно його грані є:
|
А |
Б |
В |
Г |
Д |
|
Прямокутник |
Квадрат |
П’ятикутник |
Шестикутник |
Трикутник |
6. Нехай l – довжина відрізка, а l1 – довжина його ортогональної проекції на деяку площину. Порівняйте l1 і l.
|
A |
Б |
В |
Г |
Д |
|
l1< l |
l< l1 |
l1= l |
Порівняти неможливо |
l1 |
7. Встановіть відповідності, користуючись рисунком:

- Паралельними є: А. площини MKF i MNF
- Перпендикулярними є: Б. прямі MM1 i K1F1
- Мимобіжними є: В. площини К1F1F і NN1F1
- Перетинаються: Г. прямі MN i KN
Д. прямі MN i NM
8.З деякої точки проведена похила, проекція якої дорівнює 6 см, і перпендикуляр, що дорівнює 8 см. Знайдіть довжину похилої.
9. Через центр О правильного трикутника АВС проведено перпендикуляр МО до площини АВС. Знайти градусну міру кута СМО, якщо АМ = 10 см, ОВ = 5 см
Варіант 1.
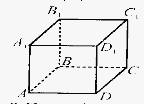
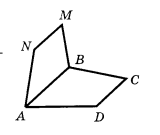
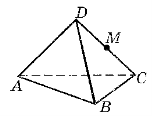
1. Якій із площин ( див. рисунок) належить точка М?
А) АDВ; Б) АВС; В) АDС; Г) не належить жодній із зображених площин.
2. Відомо,що площини α і β мають одну спільну точку. Скільки ще спільних точок
мають ці площини? А) Тільки одну; Б) тільки дві; В) тільки три; Г) безліч.
3. Через яку з наведених фігур можна провести площину і до того ж тільки одну?
А) Три точки; Б) точку і пряму; В) дві будь-які прямі; Г) дві прямі, що мають
спільну точку.
4. Точки А, В, С, D не лежать в одній площині. Серед даних прямих укажіть пряму ,
яка не лежить у площині АВD. А) АВ; Б) ВD; В) CD; Г) AD.
5. Встановіть відповідність між заданими многогранниками (1-4) та їхніми
властивостями (А-Д).
1. Прямокутний паралелепіпед. А) Має 6 ребер.
2. Трикутна призма. Б) Має 7 вершин.
3. Чотирикутна піраміда. В) Має 6 граней.
4. Тетраедр. Г) Має 8 ребер.
Д) Має 6 вершин.
6. Скільки площин можна провести через точки А, В, С, якщо АВ = 5 см,
ВС = 12 см, АС = 17 см?
7. Дві різні прямі перетинаються в точці А. Доведіть, що всі прямі, які перетинають
задані дві прямі і не проходять через точку А, лежать в одній площині.
Примітка: Завдання 1,2,3 оцінюється по 1 балу, 4,5, 6 по 2 бала, 7 - 3 бала.
Варіант 2.
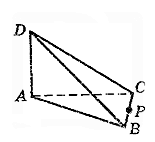
1. Якій із площин ( див. рисунок) належить точка Р?
А) АВD; Б) ВDС; В) АDС; Г) не належить жодній із зображених площин.
2. Яка з наведенмх фігур може бути лінією перетину двох площин?
А) Три точки; Б) відрізок; В) пряма; Г) будь-яка лінія.
3. Через яку з наведених фігур можна провести безліч площин?
А) Три точки, які не лежать на одній прямій; Б) дві будь-які прямі; В) прямі, що
перетинаються; Г) пряму і точку на ній.
4. Точки А, В, С, D не лежать в одній площині. Серед даних прямих укажіть пряму ,
яка не лежить у площині ВСD. А) ВС; Б) ВD; В) АD; Г) СD.

5. Встановіть відповідність між заданими многогранниками (1-4) та їхніми
властивостями (А-Д).
1. Тетраедр. А) Має 5 граней.
2. Куб. Б) Має 6 вершин.
3. Чотирикутна піраміда. В) Має 4 грані.
4. Трикутна призма. Г) Має 10 ребер.
Д) Має 8 вершин.
6. Скільки площин можна провести через точки А, В, С, якщо АВ = 5 см,
ВС = 12 см, АС = 13 см?
7. Дано пряму b і точку В поза нею. Доведіть, що пряма с, яка проходить через
точку В і перетинає пряму b, лежить із ними в одній площині.


про публікацію авторської розробки
Додати розробку
