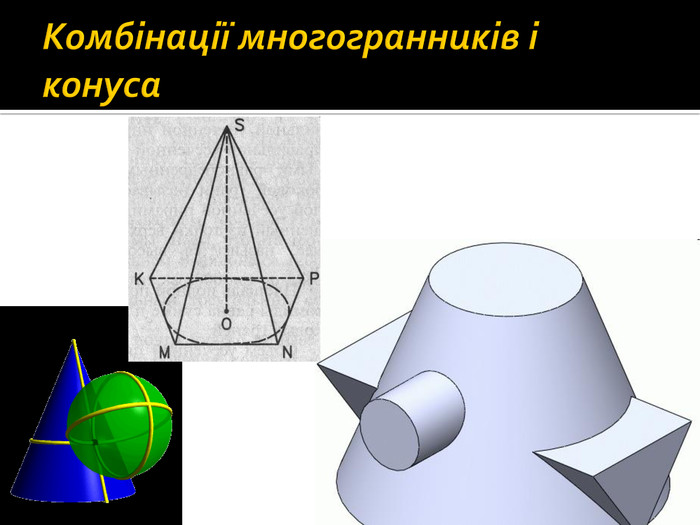
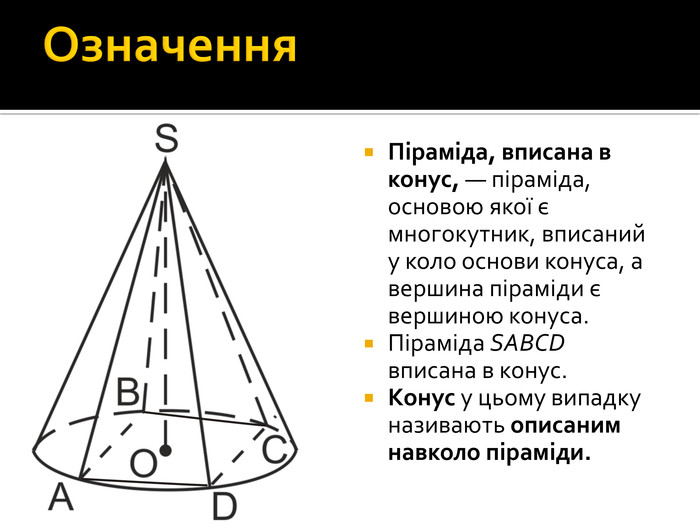
Презентація "Комбінації многогранників і конуса"
Про матеріал
Дана презентація містить основні означення, властивості, графічні зображення та задачу з розв'язком. Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку