Контрольний замір знань з предмету "Алгебра"

Контрольний замір знань з алгебри у 9-х класах

Варіант 1

І частина (5 балів)

Завдання 1- 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть правильну відповідь. Правильна відповідь кожного завдання оцінюється одним балом.

№1. Відомо, що 2 < a < 5,  8 < b < 10. Оцініть значення виразу  a + b.

     А) 7 < a+b < 18;       Б) 10 a+b 15;         В) 10 < a+b < 15;       Г) 12 < a+b < 13.

№2. Який з проміжків є розв’язком нерівності  ≥ 48 ?

А)    ;       Б) ;    В)  ;     Г) .

№3. Знайти область визначення функції  : 

А)     ;          Б)   ;            В)   ;           Г)   .

№4.  На якому з малюнків зображено графік функції ?

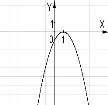
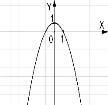
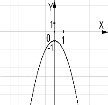
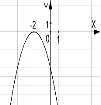 А)                              Б)                             В)                             Г) 

  №5. Не виконуючи побудови, встановіть, через яку з даних точок проходить графік   функції  у=х².

         А) D(–3;–9);                   Б) А(–2;–4);            В) С(7;–49);       Г) В(–2;4)?

ІІ частина (4 бали)

Розв’язання завдань  6 – 7  повинно мати короткий запис рішення без обґрунтування. Правильне рішення кожного завдання оцінюється двома балами.

№6.  Знайти найбільший цілий розв’язок нерівності 

                            < 3 .

№7.  Побудувати графік функції  у = х² – 4х + 3. За графіком визначити:

 а) значення у, якщо х=2;

 б) значення х, якщо у=3;

в) нулі функції.

ІІІ частина (3 бали)

Розв’язання  завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу.  Завдання оцінюється трьома балами.

№8.   Розв’язати систему нерівностей :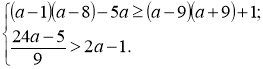    

Контрольний замір знань з алгебри у 9-х класах

Варіант 2

І частина (5 балів)

Завдання 1- 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть правильну відповідь. Правильна відповідь кожного завдання оцінюється одним балом.

№1. Відомо, що 3,2 <  x < 4,   4 < y < 7,5. Оцініть значення виразу xy.

   А) 16 <  xy < 28;            Б) 12,8 <  xy < 30;          В) 13,8 < xy < 29;       Г) 14 < xy < 32.

№2. Які з проміжків є розв'язком нерівності  –5?  

                А)                                                              В)                                              

                           –5          –2         x                                  –5            –2           x                     

               Б)                                                              Г)

                           –5          –2              х                                   –5           –2            х

№3. Виберіть правильне твердження:  вираз має зміст якщо:

        А) х(7;+∞);        Б) х(–∞;7);            В) х(–∞;7];        Г) х[7;+∞) .

  №4. Вкажіть за графіком нулі функції.

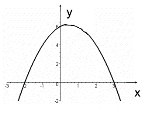                                                   А) –2; 3;         Б) –2; 6;         В) 6; 3;     Г) 3; 6.

№5. При якому значенні графік функції  у=ах² проходить через точку D(2;–8)?

          А) =2;                Б) = –2;                         В) =4;              Г) = –4.

ІІ частина (4 бали)

Розв’язання завдань  6 – 7  повинно мати короткий запис рішення без обґрунтування. Правильне рішення кожного завдання оцінюється двома балами.

№6.  Знайти найбільший цілий розв’язок нерівності 

                          > 1 .

№7. Побудувати графік функції  у = х² + 4х + 3. За графіком визначити:

        а) значення у, якщо х=2;

        б) значення х, якщо у=3;

        в) нулі функції.

ІІІ частина (3 бали)

Розв’язання  завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу.  Завдання оцінюється трьома балами.

№8. Доведіть, що система нерівностей 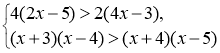не має розв’язків.