«Корінь n-го степеню. Арифметичний корінь n-го степеню та його властивості» 10 клас, алгебра
Часовоярська загальноосвітня школи І-ІІІ ступенів №17
Бахмутської районної ради
«Корінь n-го степеню. Арифметичний корінь n-го степеню та його властивості»
10 клас, алгебра
Розробив учитель математики ЗОШ №17
Чаплик Вікторія вікторівна
Урок № 1-2
Тема уроку. Корінь n-го степеню. Арифметичний корінь n-го степеню та його властивості.
Мета уроку: повторити й систематизувати значення учнів про квадратний корінь; сформулювати поняття кореня n-го степеню й арифметичного кореня n-го степеню, властивості кореня n-го степеню; формувати вміння застосовувати ці знання під час перетворення виразів. Формувати інформаційну та полікультурну компетентність.
Тип уроку: засвоєння нових знань.
Хід уроку
І. Організаційний етап
ІІ. Перевірка домашнього завдання
На попередньому уроці учні одержали завдання повторити тему «Арифметичний квадратний корінь і його властивості».
- «Асоціативний кущ» (технологія)


 (учитель пропонує учням згадати слова (словосполучення), які асоціюються зі словами «квадратний корінь з числа а».
(учитель пропонує учням згадати слова (словосполучення), які асоціюються зі словами «квадратний корінь з числа а».
![]()
![]()
![]()



![]()
![]()
![]()
![]()
![]()
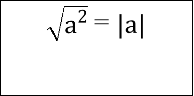


ІІІ. Актуалізація опорних знань
Математичний диктант
- Закінчить речення: «Квадратним коренем із числа а називається таке число b, що…».
- Чому дорівнює квадратний корінь із 16?
- Чи існує квадратний корінь із від’ємного числа?
- Чи існує квадратний корінь із 0?
- Закінчить речення: «Арифметичним квадратним коренем із від’ємного числа а називається…».
-
При яких значеннях а і b виконується рівняння
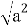 = b?
= b?
-
Чому дорівнює 2(
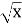 )2 (х
)2 (х 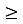 0) ?
0) ?
-
Чому дорівнює 2
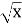 2
2
-
Знайдіть значення виразу
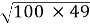 .
.
-
Обчисліть:
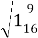 .
.
-
Обчисліть:
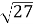
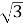 .
.
-
Знайдіть значення частки
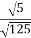 .
.
ІV. Формулювання мети і завдань уроку; мотивація навчальної діяльності
Практика розв’язування завдань з арифметичним квадратним коренем і квадратним коренем показує, що необхідно узагальнити й розширити ці поняття – ввести більш загальне поняття «корінь n-го степеню» і вивчити його властивості.
V. Сприйняття й осмислення нового матеріалу
Робота в групах
Об’єднавшись в групи діти вивчають самостійно означення кореня n-го степеню та його властивості.
1-4 групи одержують завдання: скласти «юридичну шпаргалку» (коротку наочну таблицю-схему), в якій відобразити всі відомості про корінь n-го степеню з числа а, умови його існування, арифметичний корінь n-го степеню та властивості коренів.
|
|
|
a – підкореневий вираз,
|

 n = 2k, k
n = 2k, k ![]() N n = 2k + 1, k
N n = 2k + 1, k ![]() N
N
![]()
![]()
|
( |
|
Арифметичний корінь n-го степеня з а
|
5 група працює з текстом підручника в тому ж обсязі, однак завдання у них таке: скласти запитання до означення та властивостей кореня n-го степеню, тобто створити так званий «опитувальник»:
- Дайте означення кореня n-го степеню із числа а;
- Дайте означення аргументного кореня n-го степеню із числа а;
-
При яких значеннях а існують вирази:
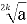 і
і 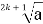 , K
, K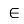 N;
N;
- Основні властивості кореня n-го степеню для невід’ємних значень підкореневих виразів.
Через певний час учні 1 – 5 групи об’єднуються в новостворені групи й демонструють один одному свої схеми та «опитувальники», разом знаходячи відповіді на всі запитання.
VІ. Первинне закріплення нового матеріалу
- Виконання усних вправ
- Знайдіть значення виразу:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г)![]() ; д)
; д)![]()
- Розв’яжіть рівняння:
а) х4 = 16; в) х7 = 8; д) х10 = 0;
б) х3 = -8; г) х8 = 1; е) х6 = -64.
- Розв’яжіть рівняння:
а) ![]() б)
б) ![]() = 1; в)
= 1; в) ![]() = -2.
= -2.
- Виконання письмових вправ
- Знайдіть значення виразу:
а) ( - ![]() )4; б )(2
)4; б )(2![]() )5 ; в) (
)5 ; в) (![]() )9.
)9.
- Знайдіть значення виразу:
а) ![]() ; б
; б ![]()
- Знайдіть значення виразу:
а) ![]() ∙
∙ ![]() ; в)
; в) ![]() ; д)
; д) ![]() .
.
б) ![]() ; г)
; г)![]() ;
;
- Спростить:
а) ![]() ; б)
; б) ![]() , m
, m ![]() d)
d) ![]() .
.
- Знайдіть значення виразу:
а) 0,6![]() -
- ![]() ; б)
; б) ![]() + 4(
+ 4(![]() )6 - 3
)6 - 3![]() .
.
ІІ. Підбиття підсумків уроку
Повторити основні етапи вивченого матеріалу.
|
Означення і властивості |
Приклади |
|
І. Означення |
|
|
Коренем n-го степеню із числа а називається таке число, n-й степінь якого дорівнює числу а (
|
|
|
Арифметичним коренем n-го степеню з невід’ємного числа називається таке невід’ємне число, n-й степінь якого дорівнює а. |
|
|
Пам’ятай! |
|
|
( |
|
|
ІІ. Властивості кореня n – го степеню (n |
|
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
= |
|
5. |
|
|
6. |
|
|
7. ( |
(2 |
|
8. |
|
|
9. |
|
VІІІ. Домашнє завдання
- Вивчити означення і властивості n-го степеню.
- Виконати вправи.
С – середній рівень
Знайдіть значення виразу:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() .
.
Д – достатній рівень
Спростить вираз:
а) ![]() ; б)
; б) ![]() , якщо х
, якщо х![]() 10; в)
10; в) ![]() .
.
В – високий рівень
Спростить вираз:
![]() , якщо с
, якщо с![]() ,
, ![]() 0, b
0, b ![]() 0.
0.


про публікацію авторської розробки
Додати розробку


