Кут. Вимірювання кутів
Тема. Кут. Вимірювання кутів
Мета: повторити, узагальнити і систематизувати знання учнів щодо означення елементів та видів кутів, а також про властивість вимірювання кутів, відомі учням з п'ятого класу, а також доповнити ці знання новим поняттям «внутрішньої області кута» та нових для учнів одиниць вимірювання кутів — мінута і секунда. Виробити первинні вміння учнів виконувати зображення кутів певного виду або певної градусної міри і позначати зображені кути, виробити вміння виконувати додавання та віднімання градусних мір кутів, що виражені в різних одиницях вимірювання.
Тип уроку: повторення, систематизація знань.
Форма проведення: фронтальна практична робота.
Обладнання: таблиці № 3 «Відрізки», № 4 «Кути».
Хід уроку
I. Організаційний етап
Учитель запрошує учнів до самоперевірки готовності до уроку і повідомляє тему і план роботи на уроці.
II. Перевірка домашнього завдання
Цей етап уроку можна провести або у формі самостійної роботи, або зібравши зошити учнів на перевірку.
Самостійна робота № 1
Варіант 1
- Точка N лежить між точками М і К. MN = 8,4 см, KM = 18,3 см. Обчисліть NK.
- На рис. 13 АС = 9 см, СB = 4 см, BD = 12 см. Знайдіть АВ, CD, AD.
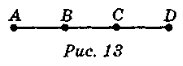
- На прямій позначено точки А, В, С, причому АВ = 24 см, BC = 18 см. Знайдіть відстань від точки А до середини відрізка ВС. Скільки розв'язків має задача?
Варіант 2
- Точка С лежить між точками А і В. АВ = 8,3 см, СВ = 4,8 см. Обчисліть АС.
- На рис. 14 LN = 15 см, NK = 16 см, MK = 24 см. Знайдіть MN, LK.
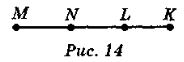
- На прямій позначено точки А, В, С, причому АВ = 24 см, а відстань від точки С до середини відрізка АВ дорівнює 17 см. Знайдіть довжину відрізка АС. Скільки розв'язків має задача?
III. Формулювання мети і завдань уроку. Мотивація навчальної діяльності учнів
Створенню позитивної мотивації навчальної діяльності учнів на уроці може сприяти робота з вивченими поняттями геометрії, а саме з поняттями точка, пряма та їх властивості, а також «відрізок та властивість вимірювання відрізків» в контексті з'ясування логічного зв'язку між ними (наприклад, складання схеми, тощо).
Схема № 2
|
Властивості та вимірювання відрізків і кутів |
||
|
Відрізки |
||
|
Вимірювання |
Властивості |
|
|
АВ = а; а > 0 |
Точка С належить відрізку
|
|
|
Кути |
||
|
Вимірювання |
Властивості |
|
|
|
α? |
? |
Згідно з логікою цієї схеми учні мають усвідомити, що наступним кроком у вивченні геометрії має бути питання про геометричну фігуру, що утворена двома променями, після чого вчитель формулює дидактичну мету уроку, а учні разом з учителем формулюють завдання на урок.
IV. Актуалізація опорних знань і вмінь учнів
Перед формулюванням означення кута, властивостей вимірювання кутів доречно буде повторити відповідні твердження для відрізків.
V. Систематизація знань учнів
План бесіди
- Означення кута. Елементи кута. Позначення кутів.
- Внутрішня область кута, її позначення.
- Розгорнутий кут.
- Градусна міра кута та її властивості. Одиниці вимірювання кутів і зв'язок між ними.
- Види кутів за градусною мірою. Інструменти для вимірювання кутів.
Таблиця № 4
|
Кути |
|
|
1. Означення |
|
|
|
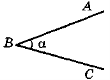
Кут ABC ( — внутрішня область кута (частина площини, обмежена променями) |
|
2. Розгорнутий кут |
|
|
|
Промені ВА і ВС — доповняльні, тому |
|
3. Вимірювання кутів |
|
|
а) одиниці вимірювання:
1° (1 градус) — це
1' (1 мінута) — це
1" (1 секунда) — це |
|
|
б) властивості вимірювання |
|
|
|
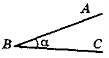
α — градусна міра кута ABC |
|
|
BD — внутрішній промінь кута ABC: |
|
4. Рівні кути |
|
|
|
|
|
|
|
|
5. Бісектриса кута |
|
|
|
BD — внутрішній промінь кута ABC, причому |
Методичний коментар
Поняття відрізка, так само, як і поняття кута, загалом відоме учням ще з п'ятого класу. Тому основна задача полягає в тому, щоб спонукати учнів до відновлення їхніх знань, і, спираючись на ці знання учнів, сформулювати достатньо строгі математичні твердження (означення та властивості).
Слід звернути увагу на те, що означення кута, яке подається в підручнику, відрізняється від традиційного (це буде перший новий момент), а також уже на цьому уроці учні знайомляться з такими одиницями вимірювання кутів, як мінута і секунда (це буде другий новий момент).
VI. Закріплення знань, усвідомлення нового матеріалу
 Усні вправи
Усні вправи
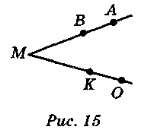
- Чи можна кут, зображений на рис. 15, позначити так:
![]() AOM ,
AOM , ![]() AMO,
AMO, ![]() AMB,
AMB, ![]() OMA,
OMA, ![]() MOA,
MOA, ![]() AMK,
AMK, ![]() OMK,
OMK, ![]() ABO,
ABO, ![]() KMB,
KMB, ![]() OKA?
OKA?
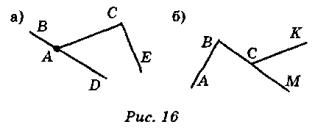
- Назвіть усі кути, зображені на рис. 16.
- Назвіть вісім кутів, що зображені на рис. 17.

Письмові вправи
- Графічні вправи № 67, 69, 71.
- На закріплення знань про нові одиниці вимірювання кутів Х° 73, 75 (б).
VII. Підсумки уроку
На рис. 18 зображено кути. Які з них можна вважати зображенням кута: 30°, 172°, 179 градусів 60 мінут, ![]() розгорнутого кута?
розгорнутого кута?
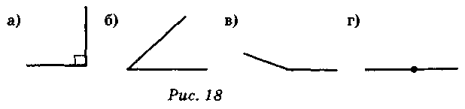
VIII. Домашнє завдання
- § 3, с. 19—22 — вивчити теорію.
- Письмово: № 68, 70, 74, 90.


про публікацію авторської розробки
Додати розробку