Квадратне рівняння як математична модель текстових і прикладних задач

Тема: «Квадратне рівняння як математична модель текстових і прикладних задач»

Тип уроку:  засвоєння знань та вмінь.

Наочність та обладнання:  ПК, проектор, екран, прапорці різних кольорів.

Мета уроку: навчити розв’язувати квадратні рівняння.

Завдання уроку:

• формувати вміння розв'язувати текстові і прикладні задачі за допомогою квадратних рівнянь;
•  виховувати в учнів потяг до наукової творчості;
•  розвивати уявлення про роль математики у пізнанні навколишнього світу, як  його невід’ємну складову.

                                              Хід уроку.

І. Організаційний момент (1хв.).

ІІ. Формулювання теми,  мети, мотивації та завдань уроку

 (5 хв.).

ІІІ. Актуалізація опорних знань і умінь (10 хв.).

ІV. Формування вмінь. Командна гра «Дискримінантний бій» (25хв.).

V. Підведення підсумків уроку ( 2хв.).

VI. Рефлексія (2 хв.).

VIІ. Домашнє завдання ( 1хв.).

І. Організаційний момент 

Привітання. Перевірка присутніх та готовності учнів до уроку.

ІІ. Формулювання теми,  мети і завдань уроку.

Квадратні рівняння – це фундамент, на якому знаходиться величний храм алгебри. Важливість вміння розв’язувати квадратні рівняння ще раз доказує те, що такі рівняння вміли вирішувати вже  в далеку давнину. До цього їх спонукала необхідність розв’язування задач, пов’язаних із знаходженням площ земельних участків та земляними роботами воєнного характеру, а також розвиток астрономії, та власне математики.

Цікаво знати, що:

1.                   Траєкторію руху планет можна описати квадратним рівнянням (слайд 5).
2.                   Літак при злеті і посадці рухається по параболі, тобто його рух також можна задати квадратним рівнянням (слайд 6).

Можливо вам відомі ще якісь приклади? Назвіть їх?

Отже, я пропоную вам долучися до  розв’язування задач за допомогою квадратних рівнянь. Тема нашого уроку «Квадратне рівняння як математична модель текстових і прикладних задач».

ІІІ. Актуалізація опорних знань і умінь.

Щоб згадати раніше вивчений матеріал, пропоную розгадати й заповнити кросворд. Якщо правильно дати всі відповіді, то у виділених клітинках ми отримаємо слово, яке є ключовим при розв’язуванні рівнянь другого степеня. 

1.                   Скільки коренів має квадратне рівняння, якщо дискримінант більше нуля.
2.                   Якому числу дорівнює вільний член рівняння .
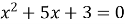3.                   Не розв’язуючи рівняння,  скажіть, чому дорівнює добуток коренів рівняння .
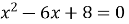4.                   У квадратному рівнянні 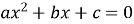числа a,b,c – це …
5.                   Як називають рівність з невідомою змінною?
6.                   Коли дискримінант дорівнює нулю, скільки розв’язків має рівняння?
7.                   За теоремою Вієта: ______ коренів зведеного квадратного рівняння дорівнює  протилежному значенню другого коефіцієнта.
8.                   Значення, при якому рівняння перетворюється в правильну числову рівність – це  ____ рівняння.
9.                   Квадратне рівняння, у якого перший коефіцієнт дорівнює одиниці, називають ______.
10.               Графіком функції 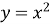є _________.
11.               Квадратне рівняння, в якому один з коефіцієнтів дорівнює нулю називають _______.
12.               Прізвище вченого, що вивів формули, які відображають корені рівняння через його коефіцієнти.

Після заповнення кросворду необхідно обговорити, яке отримали ключове слово. Опитати учнів на знання формули для знаходження дискримінанту та коренів квадратного рівняння.

ІV. Формування вмінь. Командна гра «Дискримінантний бій».

Учні, пропоную вам за допомогою квадратних рівнянь розв’язати прикладні задачі, які знаходять своє відображення у житті. Для цього спочатку потрібно створити її математичну модель, тобто записати залежність між відомими і невідомими величинами за допомогою формул, рівнянь тощо. А потім знайти розв’язки, отриманої залежності і зробити висновки.

Для роботи клас ділиться на 3-4 групи. Кожна група назначає капітана команди. Їм видаються прапорці різного кольору. На проекторі з’являються по черзі завдання для команд. Задача команд полягає в тому, щоб найскоріше запропонувати розв’язання. Хто перший впорався – піднімає прапорець. Капітан назначає доповідача команди, який представляє рішення на дошці. Розв’язок звіряють з правильною відповіддю на слайді. Доцільно провести дискусію з приводу кожної задачі, де кожна команда робить зауваження або вносить свої корективи. Якщо команда правильно відповіла, то вони вважаються переможцями цього раунду.  За результати всіх етапів оголошують переможців гри.

Раунд 1

Задача 862. с. 163

Одне з двох натуральних чисел на 5 менше від другого. Знайдіть ці числа, якщо їх добуток дорівнює 204.

Щоб перейти до раунду 2, командам пропонується відповісти на питання.

Посилаючись на малюнок, дайте відповідь, скільки розв’язків має квадратне рівняння?

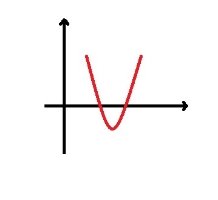
Команда, що дала правильну відповідь отримує додаткові бали.

Раунд 2

Задача 864 с. 193

Знайдіть периметр прямокутника , якщо його площа дорівнює 108 см², а одна зі сторін на 3 см більша за другу.

Для того, щоб дізнатися умову третьої задачі, необхідно знайти рішення задачі.

Знайти другий корінь квадратного рівняння, якщо , а

.

Право відповіді надається команді, що перша підняла свій прапорець. За правильну відповідь команда отримує додатковий бал.

Раунд 3

Задача 875. с. 164

Дві дороги перетинаються під прямим кутом. Від перехрестя доріг одночасно рушили два велосипедисти, один у східному напрямку, другий у північному. Швидкість першого була на 4 км/год більшою за швидкість другого. Через 2 години відстань між ними становила 40 км. Якою була швидкість кожного з велосипедистів?

Команда , яка перемогла, отримує оцінки високого рівня. Крім того, кожній команді дається пропозиція назвати найбільш корисного гравця, який також може бути відзначений оцінкою.

V. Підведення підсумків уроку

Таким чином, ми навчилися за допомогою квадратних рівнянь розв’язувати різноманітні прикладні задачі.

Квадратні рівняння широко застосовуються у різних сферах нашого життя. Наприклад, у біології, фізиці, хімії, астрономії.

VI. Рефлексія

Шановні учні, в завершенні нашого уроку, я прошу вас продовжити речення.

Я навчився ….

Я зрозуміла….

Мені сподобалося….

Мені не сподобалося….

Я хотів би …..

VІІ. Домашнє завдання.

Опрацювати § 23 за підручником О.С.Істера «Алгебра, 8 клас», знати методи розв’язання основних типів задач. Виконати письмово №863, 876, 878.