Квадратні корені. Дійсні числа
Тема: Розв’язування вправ з теми «Квадратні корені. Дійсні числа»
Мета: повторити, узагальнити та систематизувати знання учнів про квадратні корені; вдосконалювати вміння і навички виконання тотожних перетворень виразів, що містять квадратні корені; сприяти формуванню та розвитку інтелектуальних та творчих здібностей учнів, розвивати логічне мислення, пам’ять, обчислювальні навички; виховувати організованість, уважність, відповідальність, пізнавальну активність, колективізм.
Обладнання: мультимедійне обладнання, комп’ютерна презентація, роздатковий матеріал.
Тип уроку: урок систематизації й узагальнення вивченого матеріалу.
Форми роботи:фронтальна, індивідуальна, групова, робота в парах.
Хід уроку
І. Організаційний етап
Добрий день, дорогі діти, шановні гості.
Всі готові? Можемо розпочинати урок.
Розпочати наш з вами урок я хочу з такого питання. Завдяки чому людина може здобути визнання? Які складові успіху? Американський винахідник Томас Едісон так оцінював складові своїх успіхів: «У моїх винаходах було дев'яносто відсотків праці в поті чола. Решта припадають на талант, натхнення, інтуїцію та інші випадковості». Так можна сказати про кожну визначну людину
Народна мудрість говорить: «Хочеш бути щасливим – не будь лінивим». Це так, бо все у світі здобувається працею. Щоб досягти успіху, ось вам моя порада: будьте:
П рацьовитими
О рганізованими
Р ішучими
А ктивними
Д опитливими
А куратними у роботі
Є одна особливість вивчення математики – послідовність сприйняття. В математиці неможна йти далі, якщо не засвоїти попереднього. Тож на сьогоднішньому уроці «розв’язування вправ з теми «Квадратні корені. Дійсні числа»» ми повторимо, узагальнемо і систематизуємо знання про квадратні корені, вдосконалимо вміння і навички виконувати тотожні перетворення , будемо формувати вміння застосовувати отримані знання до розв’язування нестандартних практичних задач.
Підготуйте зошити до роботи. З метою взаємодопомоги і взаємонавчання ви будете працювати в трьох групах.
Робота в групах
Епіграфом до нашого сьогоднішнього уроку будуть слова визначного математика Математика – це не так знання, як уміння.
В. Серве .
Те, що незрозуміло, потрібно з‘ясувати. Конфуцій
Але для того, щоб їх почути, ось вам перше завдання. Кожна група отримає одинакові карточки. На одні стороні надруковані вирази на обчислення арифметичного квадратного кореня, з іншої - буква. Ваше завдання , якомога швидше знайти значення виразів і скласти їх в порядку зростання, а потім перевернувши карточки з букв, які ви побачите скласти потрібний вислів. Отже, прошу до роботи
Епіграфом до нашого уроку будуть слова: « Як приємно дізнатися, що ти чогось навчився. » Ж Мольєр, але щоб дізнатися їх вам потрібно виконати певне завдання. (кожна група одержує картки з певними виразами, які потрібно обчислити і скласти в порядку зростання. З іншої сторони картки є букви . якщо правильно скласти ряд одержимо потрібний вислів ----)
|
я |
к |
п |
р |
и |
є |
м |
н |
о |
|
- |
- |
- |
|
|
|
|
|
|
|
д |
і |
з |
н |
а |
т |
и |
с |
я |
|
- |
- |
- |
- |
|
|
|
|
|
|
щ |
о |
т |
и |
|
|
|
|
|
|
ч |
о |
г |
о |
с |
ь |
н |
а |
в |
|
- |
- |
- |
- |
- |
- |
|
|
|
|
ч |
и |
в |
с |
я |
|
|
|
|
|
|
ІІ. Актуалізація опорних знань
На домашнє завдання кожна з груп мала підготувати розповіді, історичні довідки, презентації . зараз ми заслухаємо представника кожної групи
1 – ша підготувати історичну довідку про виникнення дійсних чисел;
2 – га підготувати довідку про виникнення квадратного кореня;
3 – тя підготувати довідку про виникнення і використання поняття радикал, а також підготувати коротенький кросворд для товаришів з інших груп
Виступ «Історична довідка про квадратні корені та дійсні числа»
(презентації)
Гра «Доміно» (повторення теоретичного матеріалу)
Учні отримують картки. Картка складається з двох частин. У лівій частині записане запитання, у правій – відповідь на запитання іншої картки. Картки занумеровані. Гра полягає в тому, що учень, у якого картка під номером 1, зачитує завдання. Інші учні переглядають відповіді на своїх картках і той, у кого є правильна відповідь зачитує її, а потім читає запитання зі своєї картки. Гра продовжується доти, поки не вичерпаються всі запитання та відповіді.
|
№1 Означення квадратного кореня з невід’ємного числа. |
Треба, скориставшись основною властивістю дробу, домножити чисельник і знаменник на вираз, спряжений до знаменника. |
|
№2 Означення арифметичного квадратного кореня з невід’ємного числа. |
Треба побудувати графіки обох частин рівняння і знайти точки їх перетину. Абсциси цих точок є розв’язками рівняння. |
|
№3 Як називається функція у=х2 та її графік? |
Ліва гілка параболи у = х2 з початком в точці (0;0), повернута на 90° вправо |
|
№4 Як винести множник з-під знака кореня? |
Називається квадратичною, а її графік називається параболою. |
|
№5 У чому полягає графічний спосіб розв’язування рівнянь? |
Квадратним коренем з невід’ємного числа а називають таке число, квадрат якого дорівнює а. |
|
№6 Як позбутись ірраціональності у знаменнику дробу? |
Треба розкласти число під коренем на такі множники, щоб з одного добувався корінь і скористатися властивістю про корінь з добутку. |
|
№7 Як внести множник під знак кореня? |
Арифметичним квадратним коренем з невід’ємного числа а називається невід’ємне число, квадрат якого дорівнює а. |
|
№8 Означення спряженого виразу |
|
|
№9
Область визначення і область значення функції у = |
|
|
№10
Що є графіком функції у = |
Називають такий вираз N відносно ірраціонального виразу М, відмінний від нуля, що добуток М*N не містить радикалів |
У цей час біля дошки два учні виконують завдання «Знайди помилку»:
1-ий учень 2-ий учень
1.
; 1.
;
2.
; 2.
;
3..
; 3.
;
4.
; 4.
.
5.
. 5.
.
Ми з вами бачимо, що учні які виконували завдання «знайди помилку» використовували властивості арифметичного квадратного кореня. На дошці прикріплений плакат з табличкою «властивості арифметичного квадратного кореня», ліва частинка таблички заповнено ваше завдання заповнити праву частину
|
№ з/п |
Властивості |
|
1. |
|
|
2. |
|
|
3 |
|
|
4. |
|
|
5. |
|
|
6. |
|
|
7. |
|
ІІІ. Узагальнення і систематизація знань
Всі знання цінні, якщо вони опрацьовані на практиці. Тож давайте на прикладах розглянемо застосування властивостей арифметичного квадратного кореня.
- Усні вправи
Зараз ми з вами повторимо властивості квадратного кореня, у кожного з вас на столі лежать таблиці, які треба заповнити, спочатку записуєте властивість яку використаєте для обчислення виразу, а потім обчислити сам вираз
|
властивість |
Вираз |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ІІІ. Етап узагальнення і систематизації вивченого матеріалу
- Усне роз’язання вправ з використанням властивостей АКК:
а) 
; б) 
; в) 
.
Обчисліть кожен письмово самостійно по групах. Прокоментуйте:
а) 
;
б) 
;
в)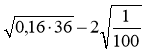 
;
г)*
(В: 13,5; 6; 2,2; 5
- Встановіть відповідність між виразами (1-3) і їм тотожно рівними (а-г):
-
; 2) 
; 3) 
;
а) 
; б) 
; в) 
; г) 
.(В: 1г ;2в; 3б)
6. Спростіть вираз:
а) 
;
б) 
;
в) 
;
г)*
. (В: 
; 9; 5; 1+
)
1). Всі знання цінні, якщо вони опрацьовані на практиці. Тож давайте на прикладах розглянемо застосування властивостей арифметичного квадратного кореня.
Колективне обговорення, запис в зошитах.
= 
= 
=
= 
= 
=
= 
= 
=
2). Тепер кожен з вас пройде тест на вміння порівнювати, співставляти.
|
№ з/п |
Властивості |
|
1. |
|
|
2. |
|
|
3 |
|
|
4. |
|
|
5. |
|
|
6. |
|
|
7. |
|
ІІІ. Етап узагальнення і систематизації вивченого матеріалу
- Усне роз’язання вправ з використанням властивостей АКК:
а) ; б) ; в) . (В: 6; 11; 72)
- Обчисліть кожен письмово самостійно по групах. Прокоментуйте:
а) ;
б) ;
в) ;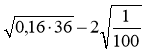
г)* (В: 13,5; 6; 2,2; 5
- Встановіть відповідність між виразами (1-3) і їм тотожно рівними (а-г):
-
; 2) ; 3) ;
а) ; б) ; в) ; г) .(В: 1г ;2в; 3б)
6. Спростіть вираз:
а) ;
б) ;
в) ;
г)*. (В: ; 9; 5; 1+)
Індивідуальна робота.
Самостійно заповнюємо табличку, вказавши номер властивості арифметичного квадратного кореня, яка використана для обчислення виразу.
|
властивість |
Вираз |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Самостійна робота
Релаксація «Шкільні жарти»:
- У 8-А класі пройшла контрольна з алгебри. Наш Назарко , стараючись добути квадратний корінь з 16, одночасно добув корінь старого пенька на шкільному подвір’ї , а також корінь зуба мудрості у своєму роті. За пеньок Назару оголошено подяку від директора школи, а за відвідування стоматолога під час уроку – «двійка» за контрольну від вчительки.
-
Доведемо, що розваги – це зло. Перш за все відомо, що розваги вимагають грошей і часу: РОЗВАГИ=ГРОШІ·ЧАС. За відомою аксіомою: «час – це гроші», маємо: ЧАС=ГРОШІ, тому РОЗВАГИ=ГРОШІ·ГРОШІ=(ГРОШІ)2. Так як за правилом: «гроші – це корінь зла», ГРОШІ=
, то РОЗВАГИ=()2. За тотожністю ()2=ЗЛО, отже, РОЗВАГИ=ЗЛО. Що й треба було довести.
Оціночний лист
Учення (иці) 8 А класу __________________________________
з теми « Квадратні корені. Дійсні числа»
|
№ |
Завдання |
Кількість балів |
|
1 |
Історична довідка |
|
|
2 |
Гра «Доміно» |
|
|
3 |
«Знайди помилку» |
|
|
4 |
Таблиця «Властивості АКК» |
|
|
5 |
Усні вправи |
|
|
6 |
Письмові вправи |
|
|
7 |
Індивідуальна робота |
|
|
8 |
Самостійна робота |
|
|
9 |
|
|
|
|
Всього |
|
Методичні прийоми використання на уроці
|
Структура уроку |
Методичні прийоми |
Хронометраж |
|
I. Організація класу до уроку |
Гра «Пароль» |
3 хв. |
|
II. Актуалізація опорних знань |
а) бліцопитування; б) математичний диктант; в) «Втрачена інформація» |
6 хв. |
|
III. Мотивація навчальної діяльності |
«Картинна галерея» |
9 хв. |
|
IV. Повідомлення теми і мети уроку |
«Очікувані результати» |
3 хв. |
|
V. Виконання завдань під контролем вчителя |
а) бліцтест; б) дидактична гра «Відповідність «Відповідь – буква»; в) «Натхнення» |
10 хв. |
|
VI. Фізхвилинка |
«Іван-покиван» |
2 хв. |
|
VII. Узагальнення та систематизація знань, умінь і навичок |
а) математичний диктант б) взаємоперевірка в) заповнення аркушів оцінювання |
7 хв. |
|
VIII. Підсумок уроку. Домашнє завдання |
а) «Шерлок Холмс»; б) «Сторінка щоденника» |
5 хв. |
Хід уроку
І. Організаційний етап
Вітання з учнями.
Перевірка відсутніх на уроці.
Підготовка робочих місць учнів
Організація уваги.
ІІ. Активізація пізнавальної діяльності учнів
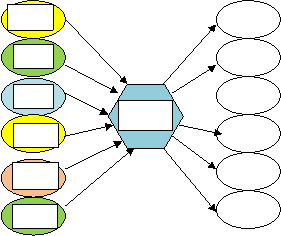Кодовані завдання.
Завдання заготовлені на дошці. Розв’язуючи їх, учні розкодовують слово «Уміння»: 5-У, 0,45-М, 0,045-І, 0,0125-Н, 0,07-Н, 2,45-Я.
Пояснюють, що таке уміння і для чого вони потрібні школярам і взагалі людям.
Так здійснюємо мотивацію навчально-пізнавальної діяльності учнів.
Налаштування на успішну роботу.
X. Підведення підсумків уроку.
Коментоване виставлення оцінок. Цінування роботи учнів на уроці.
Рефлексія.
Метод «Обери позицію»:
- Я все засвоїв на уроці. Собою задоволений!
- Мені ще треба попрацювати щоб досягти бажаного результату.
- Я у розпачі! Не знаю що робити.
Учні не тільки обирають позицію, а й обґрунтовують її (за бажанням).
Дякую за працю.
Дійсні числа
Поговоримо про історія розвитку дійсних чисел. Адже в математиці вони займають важливе місце!
Історія розвитку дійсних чисел починається з самої зорі людства. Оскільки поняття нуля було вперше (більш-менш достовірні відомості) сформульовано в 876 році від Різдва Христового та введено в Індії, можна відзначити цю дату як проміжну.
Що ж стосується від’ємних значень, то вперше їх описав Діофант (Греція) у третьому столітті нашої ери, але «узаконені» вони були тільки в Індії, практично одночасно з поняттям «нуль».
Слід пам'ятати, що історія розвитку чисел в математиці припускала їх існування ще в Давньому Єгипті, так як в результаті обчислень вони виявлялися нерідко. Ось тільки в той час їх вважали «неможливими» і «нереальними»
Квадратні корені з чисел вавилонські мате тематики вміли добувати ще в 4 тис. тому. Стародавні греки замість слів «здобути корінь» говорили « знайти сторону за даною площею квадрата», тобто раніше корінь називали «стороною». В латинській мові слова «сторона», «бік», «корінь» називаються однаково – radix.У 13 ст. європейські математики запропонували замість теперішнього писати R12 ( латинське Radix – корінь). Згодом стали замість Rписати V7, V(a+b). Декарт (1596-1650) створив знак кореня з рискою
Источник: http://5fan.ru/wievjob.php?id=53828
|
№1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в+ 
≈
- 
-
-
В л а с т и в о с т і
-
- -
-
А р и ф м е т и ч н о г о
- -
-
-
К в а д р а т н о г о
-
-
- 
К о р е н я
Історична довідка
Графічне розв’язання рівняння х²=2 показує, що існують відрізки, довжини яких не виражаються раціональними числами, тобто для вимірювання відрізків раціональних чисел недостатньо.
Цей факт було відкрито в школі великого давньогрецького вченого Піфагора.
Спочатку піфагорійці вважали, що для будь-яких відрізків завжди можна знайти такий відрізок, який у кожному з них вкладається ціле число разів. Звідси випливало, що відношення довжин будь-яких двох відрізків виражається відношенням натуральних чисел, тобто раціональним числом.
Проте самі ж піфагорійці зробили видатне відкриття. Вони довели, що діагональ і сторона квадрата не спільномірні, тобто якщо сторону квадрата взяти за одиницю, то довжину діагоналі квадрата виразити раціональним числом не можна.
1
про публікацію авторської розробки
Додати розробку