"Квадратні нерівності. Розв'язування квадратних нерівностей"

Тема. Квадратна нерівність. Розв’язування  квадратних  нерівностей

Мета: удосконалити вміння розв’язувати квадратні нерівності за допомогою графіка квадратичної функції; сформувати вміння розв’язувати нерівності методом інтервалів. Розвивати логічне мислення учнів,  пам’ять,  увагу, пізнавальну активність , виховувати культуру мовлення, дисциплінованість, навички співпраці.

Тип уроку: комбінований

Учні повинні знати: які нерівності називаються квадратичними, що означає розв’язати квадратичну нерівність, чим і як визначають наявність і кількість нулів квадратичної функції y=ax²+bx+c , алгоритм розв’язування квадратичних нерівностей графічним способом.

Учні повинні навчитися: розв’язувати квадратні нерівності з однією змінною та ілюструвати розв’язання графічно, записувати відповідь, застосовувати розв’язання квадратичних нерівностей під час знаходження області визначення функції та дослідження квадратних нерівностей з параметрами.

Обладнання та наочність: таблиця « Розв’язування квадратних нерівностей», трафарет « Парабола» , мультимедійний проектор картки з  текстовими завданнями y=x² .

Хід уроку

1. Організаційний   етап  уроку

Підготовка класної дошки до уроку, перевіряю готовність і присутність учнів.

2. Перевірка домашнього завдання.

1. Актуалізація опорних знань і перевірка домашнього завдання
2. Виконання тестових завдань

Варіант 1

1. Яка з наведених нерівностей не є квадратною?

А) x²+2x>x²+1      Б)  x²+3x>2   В)x²+4x>2x²   Г)x²+4x+x²>0.

2) Яке з наведених чисел не належить множині розв’язків нерівності x²+6x+8≤0?

 А) -3;      Б) -1,5;    В) -2;      Г)-3,99.

3) Розв’яжіть нерівність x²-5x-50>0.

А)   (-∞;-5);     Б) (-5;10);     В)   (-10;5)   Г)  (-∞; -10) U (5;+∞).

4) Знайдіть область визначення функції  f(x)=

А)  (-∞;+∞);    Б) [-2;12];  В) (-∞;-2] U [12;+∞);  Г) (-2;12).

Варіант 2

1. Яка з наведених нерівностей не є квадратною?

А) x²+5x-8 >x²;   Б) x²+4x>-x² ;  В) 2x+3>x² ;  Г ) x²+9x>2x² .

2) Яке з наведених чисел не належить множині розв’язків нерівності x²+6x+5≤0?

А) -4;   Б) -1,7;  В) -5;  Г) -.

3) Розв’яжіть нерівність x²-9x-36>0.

А) (-3;12) ; Б) (-12;3) ; В) (-∞;-3) U(12;+∞); Г) (-∞;-12) U(3;+∞).

4) Знайдіть область визначення функції f(x)=

А) (3;8);  Б) (-∞;-8) U(-3;+∞);  В) [3;8];  Г) [-8;-3].

Запитання

1. Дайте означення квадратної нерівності.
2. Які нерівності називаються строгими?
3. Як позначаються точки на числовому промені під час  розв’язування  строгих, нестрогих нерівностей?
4. Що є графіком  квадратної нерівності?
5. Як визначити напрям віток параболи?
6. Сформулюйте алгоритм розв’язування квадратної нерівності.
7. Розв’яжіть усно квадратні рівняння:  а) x² =9   б) x²-3x=0.
8. В якому випадку повне квадратне рівняння має два дійсні корені, один корінь, не має коренів?
9. Робота за таблицею. « Розв’язування квадратних нерівностей ».
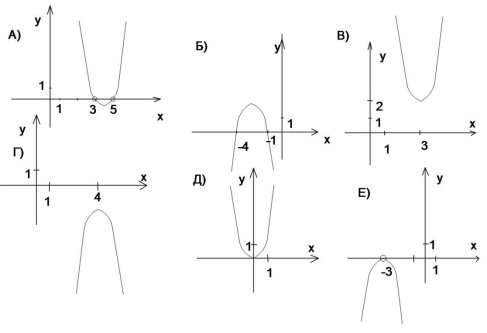
10. Для кожного з графіків укажіть множину розв’язків нерівностей ( див. таблицю).

ax²+bc+c>0     і  ax²+bx+c<0.

( Троє учнів біля дошки розв’язують завдання)

А) 3 x² -10x+3>0

Б) 6x²-13x+5≤0

В)  -x²+6x+7<0

III. Повідомлення теми і мети уроку.

IV .Практична робота

Удосконалення вміння розвязівати квадратні рівняння за допомогою графіка квадратної функції.

Розв’язати нерівності ( на  дошці умови для двох варіантів. З кожного варіанту учень виконує завдання на дошці, решта учнів на місці у зошитах свої варіанти завдань).

                I  варіант                                                                                    II  варіант

1)x²+6x+8≥0                                                                                              1) x²-3x+2≤0

2)2x²>18                                                                                                     2) -2x²≤3x

3)-x²-2x+3>0                                                                                               3) x²+5x-14≤0

4)(2x-1)(2x+1)>2(x+0,5)²                                                                     4) (x-3)(2x+5)<x(x+1)

5)                                                                         5)            

(Завдання оцінються   по 2 бали кожне.  Хто швидше закінчить одержують на 1 бал більше, ніж всі останні.)

“Я зможу”:

(Робота з усім класом).

1. Знайти усі значення х, при яких виконуються обидві нерівності:  2х²-5ч-3≤0 і  3+5х-2х²≤0
2. Серед усіх х , які задовольняють нерівність 2х²-9х+4≤0 знайти ті значення х, які не задовольняють нерівність ( х-4)(1-2х)>0.
3. Дано функцію  f(х)=5+4x-x².  Знайти  усі значення х, при яких:    а)f(x)≥8;    б)f(x)<9;  в)f(x)>10.
4. Знайти область визначення функції

y=

Розв’язання

-2x²-3x+14>0

2x²+3x-14=0

Д=9+112=121

X₁=

X₂=

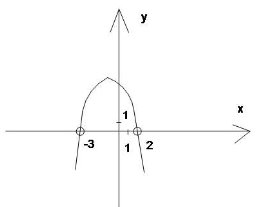
Відповідь: х є ( -3,5;0) U (0;1,5) U (1,5;2)

5. При яких значеннях а дана нерівність виконується при всіх дійсних значеннях х :

Х²-4х+а>0

Розв’язання

Д=в²-4ас

Д=16-4а

Так як I коефіцієнт а=1>0, то вітки параболи направлені вверх, а нерівність більша нуля, то точки ( перетину з віссю х немає.)

   16-4а<0

 -4а<-16

     а>4

Відповідь: при а>4.

V. Підбиття підсумків уроку.

( Інтерактивна вправа « Незакінчені речення»)

• На уроці ми навчилися…..
• Мета уроку…
• На уроці ми набули навичок…

Оголошення оцінок за урок.

VI. Домашнє завдання.

Ст. 54 №1