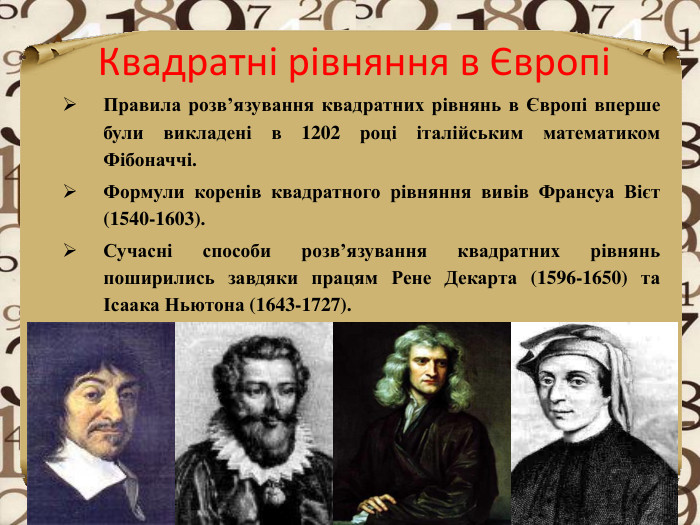
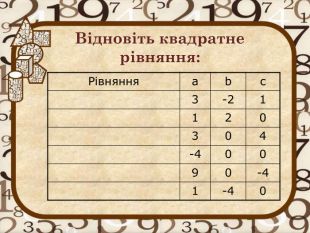
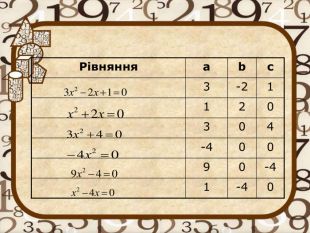
Квадратні рівняння. Формули коренів квадратного рівняння
Про матеріал
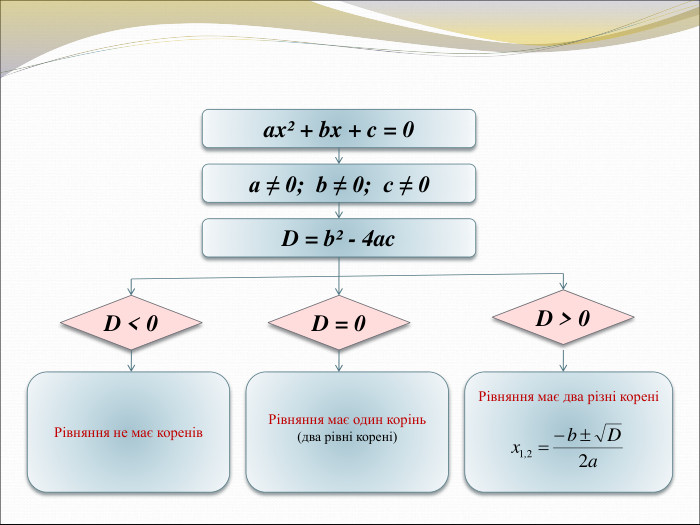
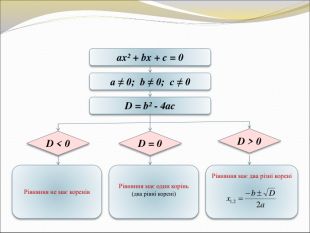
Тема. Формула коренів квадратного рівняння
Мета: Розширити та поглибити знання про розв’язання квадратних рівнянь; вивести і засвоїти формули для розв'язування квадратних рівнянь; розвивати вміння правильно та послідовно міркувати; виховувати самостійність, цілеспрямованість, сміливість, організованість.
Тип уроку: комбінований.
Наочність та обладнання: опорний конспект «Квадратні рівняння», мультимедійне обладнання, картки з завданнями.
Хід уроку
I. Організаційний етап (слайд 1)
Вітаю всіх на уроці математики і вас, діти, і наших гостей. Сьогодні ми з вами вирушаємо у подорож по цікавій країні алгебра, з багажем знань і витримкою та наполегливістю.
Оголошення теми та мети уроку (слайд 2)
Антична мудрість говорить: «Знання – це сила», на мою думку знання – це одна із сходинок до успіху. І напевно, кожний із вас зрозумів, що для того щоб досягти успіху, потрібно багато працювати. Тому епіграфом нашого сьогоднішнього уроку нехай будуть слова англійського письменника Бернарда Шоу «Єдиний шлях, що веде до знань - діяльність» (слайд 3)
Я вам хочу побажати впевненості , творчої роботи та гарного настрою на уроці, адже кожну справу, аби вона мала успіх, потрібно починати з позитивом. Я буду вашим помічником, а девізом уроку будуть слова Оноре де Бальзака «Щоб дійти до мети, перш за все треба йти». (слайд 4)
II. Актуалізація опорних знань учнів
Ми продовжуємо вивчати розділ «Квадратні рівняння»
На попередньому уроці ми вивчали з вами неповні квадратні рівняння та методи їх розв’язування. Давайте згадаємо деякі основні відомості про рівняння.
1) Фронтальне опитування учнів (слайд 5)
- Що називається рівнянням?
- Що називається коренем рівнянням?
- Що означає розв’язати рівняння?
- Які рівняння називають квадратними?
- Як називають коефіцієнти квадратного рівняння ах2+вх+с=0?
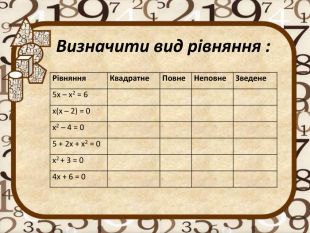
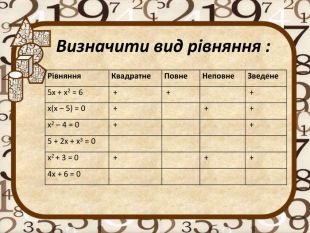
- Які існують види квадратних рівнянь?
- Яке квадратне рівняння називають зведеним?
- Яке квадратне рівняння називають неповним?
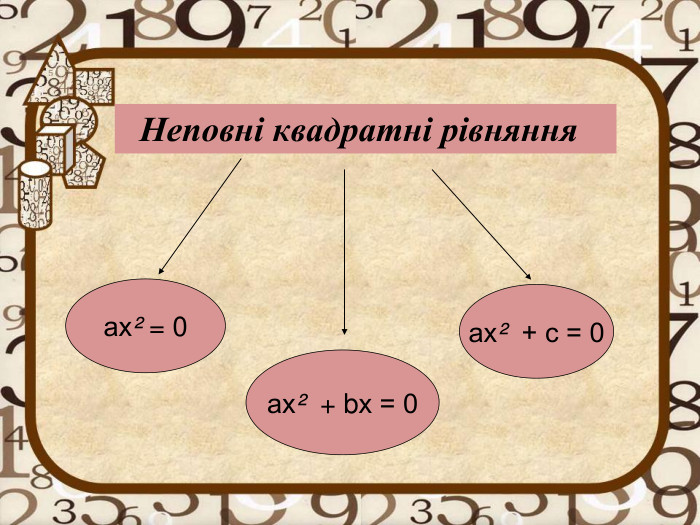
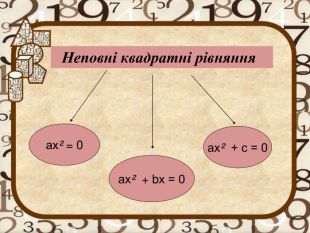
- Які існують види неповних рівнянь? (слайд 6) -- види неповних рівнянь
Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку