Квадратні рівняння. Повні та неповні квадратні рівняння

Вчитель: Заєць Марія Олександрівна

Урок Алгебри у 8 класі

Тема: «Квадратні рівняння. Повні та неповні квадратні рівняння.»

Мета: сформувати поняття про квадратне рівняння, види квадратних рівнянь та способи їх розв’язання; сформувати вміння розпізнавати повні та неповні квадратні рівняння, визначати їх коефіцієнти; виробити вміння розв’язувати неповні квадратні рівняння; розвивати логічне мислення, уважність і самостійність; виховувати спостережливість та увагу.

Тип уроку: урок засвоєння нових знань, умінь та навичок.

Обладнання: комп’ютер, опорні схеми, мультимедійна презентація, плакат, тести.

Девіз уроку: Думай і роби, роби і думай.

                                                         І. А. Крилов.

Епіграф: Ніколи не втрачай терпіння – це останній ключ, що відкриває двері.

                                                        Антуан де Сент-Екзюпері.

Хід уроку

1. Організаційний момент.

Привітання вчителя з учнями, перевірка готовності до уроку.

2. Перевірка домашнього завдання.
3. Мотивація навчальної діяльності учнів.

В ньому є щось невідоме.

Його треба розв’язати,

Тобто корінь відшукати.

Кожен легко, без вагання

Відповість, що це …

                                               (Рівняння)

Історична довідка

Розв’язувати квадратні рівняння вміли ще у Стародавньому Вавилоні за 2000-1700 до н.е. Займалися вивчанням квадратних рівнянь такі видатні математики минулого як Евклід і Діофант, Омар Хайям і Франсуа Вієт, Рене Декарт І Нільс Абель.

Французького математика Франсуа Вієта називають «батьком» алгебри. Він першим почав у рівняннях позначати буквами не тільки змінні, а й коефіцієнти, що дало можливість узагальнити способи розв’язування рівнянь.

4. Актуалізація опорних знань.

Фронтальне опитування:

•                   Що таке рівняння?
•                   Що називається розв’язком рівняння?
•                   Що означає розв’язати рівняння?
•                   Які рівняння ви знаєте та як їх розв’язувати?
•                   Які рівняння називаються лінійними? Наведіть приклади.
•                   Які рівняння називаються рівносильними? Наведіть приклади.
•                   Які рівняння називаються дробово-раціональними та вкажіть способи їх розв’язання. Наведіть приклади.

5. Вивчення нового матеріалу. Формування вмінь.

План:

1. Основні поняття теми.
2. Види квадратних рівнянь.

а) повні квадратні рівняння;

б) неповні квадратні рівняння;

в) зведені квадратні рівняння.

3. Способи розв’язування квадратних рівнянь.

а) виділенням квадрата двочлена;

б) за формулами;

в) за теоремою Вієта.

1. Основні поняття теми:

Означення 1. Рівняння. У якого ліва частина – многочлен другого степеня відносно невідомої змінної, а права – нуль, називають рівнянням другого степеня або квадратним.

Означення 2. Квадратним рівняння називають рівняння ах² + bx + c = 0, де  х – змінна, а, b, с – деякі числа, причому а≠0.

Числа а, b, с, - коефіцієнти рівняння:  а – перший коефіцієнт, b – другий, с – вільний член.

На уроках ми будемо користуватися другим означенням.

2. Види квадратних рівнянь:

а). Повні квадратні рівняння

Дискримінантом (дискримінант - discriminant) рівняння ax²+bx+c=0 називають вираз D=b²-4ac. 

a)Якщо D>0 рівняння ax²+bx+c=0 має два розв'язки, які знаходяться за формулами: 
                                     .

b)Якщо D=0 рівняння ax²+bx+c=0 має один розв'язок, який знаходиться за формулою:  .

c)Якщо D<0 рівняння ax²+bx+c=0 не має жодного розв'язку.

Розв’язання повних квадратих рівнянь:

1) x²+4x-21=0. 
Розв'язання :
D=4²-4·1·(-21)=16+84=100>0. 

х_1,2=
x₁=3, x₂=-7. 
Відповідь: x₁=3, x₂=-7.

2)x²-6x-7=0. 
Розв'язання:
D=6²-4·1·(-7)=36+28=64>0. 

х_1,2=
x₁=-1 x₂=7. 
Відповідь: x₁=3, x₂=-7.

б). Неповні квадратні рівняння

Означення. Якщо в рівняння  ах ² + bx + c = 0 хоча б один із коефіцієнтів або с дорівнює 0, то таке квадратне рівняння називається неповним.

Опорна схема

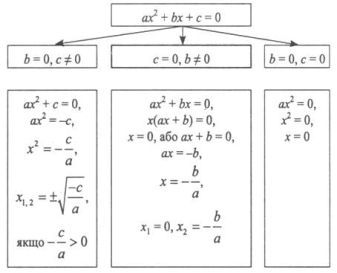
Розв’язання неповних квадратних рівнянь:

1). Розв’язати рівняння (із відповідними записами на дошці)

2). Розв’язати рівняння (самостійно, з наступною перевіркою)

Усний рахунок:

Розв`язати рівняння, записані на дошці:

- х² + 9х = 0,     19х – х² = 0,     х² – 64 = 0,     11х² = 0,     х² + 4 = 0.

в). Зведені квадратні рівняння

Квадратне рівняння називається зведеним, якщо його перший коефіцієнт дорівнює одиниці (а = 1)

х² +bх+с=0

Розв’язання рівнянь, що зводяться до неповних квадратних

1.  Розв’язати рівняння:

           а) (х-2)(х+2) 2х²-13                 б) (х-3) ² = 25 – 6х

Розв’язання:

а) (х-2)(х+2) =2х² - 13

х² -4=2х²-13

х²=9

х₁ =-3,   х₂=3

Відповідь: - 3; 3.

           б) (х – 3)² = 25-6х

           х²-6х+9 = 25-6х

            х² - 6х +6х  = 25-9

            х² = 16

             х_{1 =} -4;   х₂ = 4

Відповідь: х_{1 =} -4;   х₂ = 4

2.Розв’язати рівняння самостійно:

Розв’язування неповних квадратних рівнянь з параметрами

1) Розв’язати рівняння:

а) mх² – 8х = 0                     б) ах² + 20х = 0

Розв’язання:

а) mх² – 8х = 0

Якщо m=8, то маємо:

-8x = 0,

х = 0

Якщо m≠8, то маємо:

mx (x- ) = 0

mx = 0

x₁ = 0,    x₂  =

Відповідь: x₁ = 0, m=0;

                   х₂ =, якщо m ≠ 0.

б) ах²+20х = 0

  Якщо а = 0, то маємо:

  20х = 0

  х = 0

  Якщо а≠ 0, то маємо:

            ах (х+) = 0,   або х+=0

             х₁ = 0                       х₂ = -

Відповідь: х₁ = 0, якщо а=0;

          х₂  =  -   , якщо а  ≠ 0.

6. Фізкультхвилинка.
7. Закріплення вивченого матеріалу .

Усні вправи:

1). Яке з даних рівнянь квадратне:

2). Назвіть коефіцієнти квадратних рівнянь:

а)7

б)

в)

г)-2

д)

в)

ж)16

з)3

3). Яке з наведених квадратних рівнянь є зведеним:

а)7

б)

в)

г)-

д)

в)

ж)16

з)3

4). Яке з наведених квадратних рівнянь є неповним:

а) х² - 3х + 4=0

г)-2х² + 8х=0

б) 2х² + х -10=0

д)х² - 4=0

в) - х² - 5х + 6=0

е)х² =0

Письмові вправи:

Розв’язати рівняння:

x²-26x+120=0

2x²+x-3=0

9x²-12x+4=0

x²+x-6=0

2x²-18=0

x²+4x-21=0 

8. Підсумки уроку.

Сьогодні на уроці ми ознайомилися з поняттями «квадратні рівняння», «неповні квадратні рівняння та навчилися розв’язувати неповні квадратні рівняння.

Запитання:

1.               Які завдання виявилися цікавими?
2.               Які завдання були для вас за складними?
3.               Чи задоволені ви своєю роботою на уроці?
4.               Які рівняння називають квадратними?
5.               На які види поділяються квадратні рівняння?
6.               Скільки дійсних коренів можуть мати квадратні рівняння?
7.               Наведіть свої приклади, які проілюструють усі випадки.
8.               Прокоментуйте види рівнянь:

 1) у² – 19 = 0;      2) 2х² – 9х -10 = 0;          3) х² – 9х = 0.

9. Домашнє завдання.

1. Опрацювати параграф 20 ст.177-179;
2. Розглянути приклади розв’язування рівнянь (приклад 1-3);
3. Виконати номери: 801, 803.