Ланцюгові дроби та їх використання

Теорія ланцюгових дробів – важливий розділ сучасної математики. Вона тісно пов'язана з теорією наближень дійсних чисел і функцій раціональними дробами та раціональними функціями, теорією динамічних систем, механікою зубчатих передач. На сьогоднішній день ланцюгові дроби найчастіше використовуються в астрономії, що пов’язано з активними польотами в космос і розвитком космічної ери.

Дана робота присвячена  ознайомленню з ланцюговими дробами та застосуванню їх  в різноманітних задачах, у тому числі і завданнях олімпіадного характеру. Матеріал розраховано для проведення факультативних занять з геометрії як 9, так і в 11 класах.

ОЗНАЙОМЛЕННЯ З ЛАНЦЮГОВИМИ ДРОБАМИ

1.1. Що таке ланцюговий дріб

Теорія ланцюгових дробів – одна з найдревніших математичних теорій. Але що ж такого дивного в цих дробах, і чим вони виділяються з-поміж інших дробів.

Ланцюгові дроби були введені в 1572 році італійським математиком Бомбеллі . Сучасне позначення неперервних дробів зустрічається у італійського математика Катальді в 1613 році. Найвеличніший математик XVIII століття Леонард Ейлер перший виклав теорію ланцюгових дробів. Роботи Ейлера з теорії ланцюгових дробів були продовжені М. Софронова (1729-1760), академіком В.М. Висковатим (1779-1819), Д. Бернуллі (1700-1782) та іншими вченими. Багато принципових результатів даної теорії належать французькому математику Лагранжу.

 Для того, щоб показати що таке ланцюговий дріб почнемо з прикладу. Візьмемо, на приклад, дріб . Його можна виразити як:

                      = 3 + ( < 1)        

                   «Перевернемо» дріб :

                        = 3 + = 3 +

Дріб аналогічно як і в минулому разі виражаємо виразом:

                        = 2 +

  Отже наш дріб тепер має такий вигляд:

                         3 +

Це і є ланцюговий дріб для числа , і , до речі вже зараз, за допомогою отриманих результатів ми можемо зробити деякі висновки щодо ланцюгових дробів. Наприклад, ми можемо сказати що приблизно дорівнює 3, чи дробу 3 +, проте дорівнює  3 + . Отже, робимо висновки, що чим довше ми будемо продовжувати наш дріб, тим точніший буде результат . Ще що таким способом можна записати всі числа. Проте, якщо число ірраціональне то дріб буде нескінченним .

1.2.  Визначення ланцюгового дробу

Будемо розглядати  нескоротні звичайні дроби вигляду . Нескоротність означає, що  НСД(m,n)=1. Ця умова не обмежує класу задач, бо якщо чисельник і знаменник мають спільний дільник, більший 1, то дріб можна скоротити на такий дільник. Це робитимемо до того часу, поки дріб не стане нескоротним.

Найбільший спільний дільник ми шукали за допомогою алгоритму Евкліда. При цьому нас цікавила остача від ділення і не цікавила частка. Якщо при діленні а на b частка дорівнює m, а остача r, то:

.

Цю рівність можна записати також у вигляді

.

Враховуючи це, розглянемо наступні перетворення нескоротного дробу.

.

Ми можемо робити такі перетворення до того часу, поки чисельник нового дробу – нова остача в алгоритмі Евкліда, – не стане рівним 1. Далі ці перетворення не мають сенсу, бо на наступному етапі уже не матимемо дробу і перетворювати буде нічого.

Отже, можемо записати

.

Це – зображення нескоротного звичайного дробу ланцюговим дробом.

Як побудувати таке зображення для довільного нескоротного дробу?

Будемо шукати  НСД(39,17) .

Бачимо, що числа 2, 3, 2 та 2, за допомогою яких побудовано ланцюговий дріб, є послідовними частками в алгоритмі Евкліда.

Ланцюговим або неперервним дробом називається вираз

                                (1.1)

де а – ціле число, а a₁, a₂,...,a_n – натуральні числа.

Для зручності запису ланцюговий дріб (1.1) можна позначати і так:

.

У цьому записі ціле число відділяється крапкою з комою, а інші числа – комами.

Отже,  При цьому говорять, що звичайний дріб  розклали в неперервний дріб .

ВИКОРИСТАННЯ ЛАНЦЮГОВИХ ДРОБІВ

2.1. Ланцюгові дроби в літочисленні

Із астрономії відомо, що рік має 365,24220... “середніх” діб. Таке складне відношення довжини року до доби неможливо використовувати для літочислення. Його завжди заміняли більш простим, втрачаючи точність. При цьому з року в рік похибка накопичується. Щоб її компенсувати, до одного з року додають один день, і такий рік називається високосним.

Розкладемо число 365,24220 у ланцюговий дріб:

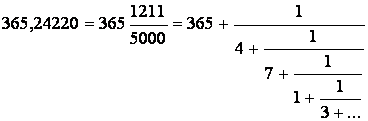
Знайдемо перші чотири наближення – перші чотири наближені ланцюгові дроби:

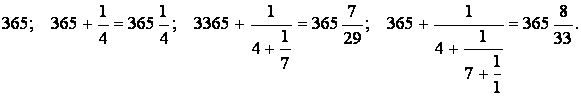
Наближення  було відоме ще стародавнім народам – єгиптянам, вавілонянам, китайцям та ін. Проте вони не мали регулярних високосних років.

7 березня 238 року до Р. Х. вийшов Канопський декрет єгипетського царя Птоломея , яким зобов’язувалося, щоб кожний четвертий рік мав не 365, а 366 діб. Проте через 40 років цей декрет забули. Його відродив у 47 році до н.е. римський імператор Юлій Цезар, встановивши у кожному четвертому році зайвий день у лютому. Цей дань було названо bissectils, звідки й пішла назва “високосний рік”. Так з’явився старий, або Юліанський стиль.

Новий, або Григоріанський стиль використовує наближення , що значно більше як за , так і за .

 Справді,

Цей стиль відрізняється від Юліанського тим, що у ньому кожен сотий рік – не високосний, крім тих сотих років, число сотень яких ділиться без остачі на 4. Тож 1700-й, 1800-й, 1900-й роки – не високосні, а 1600-й, 2000-й – високосні. Тому 400 років у Григоріанському календарі мають 97 “зайвих” діб, а не 100, як у Юліанському.

Уже в XV столітті було помічено відставання Юліанського календаря (тоді на 10 діб) і було запропоновано реформувати календар. Але ця реформа була проведена лише у кінці XVI століття. У католицьких країнах вона була запроваджена буллою папи Георгія XIII від 1 березня 1582 року. Десять діб – з 5 по 14 жовтня були викреслені з календаря. Тож 5 жовтня 1582 року всі зобов’язані були вважати, як 14 жовтня. Цим календарем ми користуємося і сьогодні.

2.2.  Наближення числа  звичайними дробами

Знайдемо найпростіші наближення знаменитого числа  – відношення довжини кола до його діаметра.

Відомо, що=3,141 592 653… Отже,

Запишемо десяткові дроби у лівій та правій частинах цієї нерівності у вигляді ланцюгових дробів:

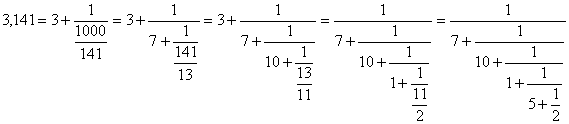
та

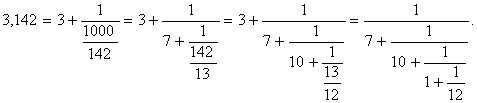
Спільна частина цих розкладів дає наближення: Це наближення знайшов ще Архімед, який жив у III столітті до нашої ери. Оскільки , а ,то наближення Архімеда є точніше, ніж зазвичай використовуване наближення . Воно є точним до трьох знаків після десяткової коми і похибка від використання цього наближення менша, ніж  .

Взявши для числа  наближення

таким же способом отримаємо:

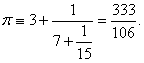
Оскільки , то це наближення дає чотири правильні цифри після десяткової коми і має похибку меншу, ніж .

Якщо взяти наближення

то отримаємо таким же способом ланцюговий дріб

Це наближення дає похибку  , яка не перевищує . Його знайшов ще у давні часи римський філософ Адріан Мецій.

2.3. Застосування ланцюгових дробів в астрономії

Використання ланцюгових дробів поширене у  небесній механіці та астрономії, де вони використовуються для прогнозу сонячних чи місячних затемнень, руху планет і інших періодичних подій. Наприклад, співвідношення обертання довкола сонця Юпітера та Сатурна приблизно дорівнює відношенню два до п’яти, але точно ми не можемо сказати, оскільки кожні вісімсот років ці планети так близько наближуються одна до одної, що впливають на траєкторію та швидкість обертання один одного. Для розрахунку таких періодів і використовуються ланцюгові дроби.

  Розглянемо приклад, при якому дві планети обертаються в одну сторону навколо зірки, коли співвідношення періодів їх руху з великою точністю дорівнює раціональному числу, наприклад , то ці дві планети будуть розташовані на мінімальній можливій відстані одна від одної лише в трьох певних точках.

Мал. 3 

                                                                                                Рис.2.1

Інша справа коли відношення періодів обертання раціональне число з великим знаменником. Візьмемо, наприклад число . Тоді виходить, що точок збільшеної гравітації аж цілих 213110, і точки взаємовпливів цих двох планет стає аж занадто «розмазаним», що не є гарною новиною для астрономів.

 Саме тому астрономи почали задавати собі питання, які ж величини цих, як іноді кажуть, «неповних» часток (елементів) ланцюгового дробу, тобто якщо

а = а+ ,

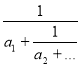наскільки великі числа а, а, а, … якщо число а – випадкове дійсне число [1]. Нехай якесь з цих чисел, візьмемо а, дуже велике, наприклад мільйон, тоді наближення аа + (яке ми отримаємо при обриванні дробу перед а) буде неймовірно точним. Якщо ж а буде дорівнювати всього лише 2, то помилка буде доволі великою. Саме тому питання про те, чи збільшуються коефіцієнти, і з якою швидкістю вони це роблять, має реальне астрономічне, і до того ж дуже важливе значення на долю всього Всесвіту, а отже і нашої галактики, Сонячної системи та цивілізації.

Перше математичне дослідження цього важливого питання проводив астроном Х. Гільден,  котрий опублікував його у доповідях Паризької академії наук в 1888 році .

2.4.  Використання ланцюгових дробів в геометрії

Існує дуже цікаве число (про яке було відомо ще за часів існування давньої Греції), у якого в ланцюговому дробі всі числа дорівнюють 1:

1 +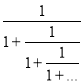

Позначаємо це число за х. Тоді воно задовольняє рівність:

1 + =х    х – х +1 = 0

І з цього ми можемо зробити висновок, що х = . А оскільки х повинен бути додатнім, х = (1,6) .

Це число вже має свою назву , а саме -   золотий переріз. Це дуже «гарне» число, оскільки його пропорції фізіологічно позитивно впливають на людину. Можливо саме тому листівки роблять в формі прямокутника, відношення сторін якого дорівнюють цьому числу. Якщо відрізати від такого прямокутника квадрат  зі стороною рівній його меншій стороні, то в отриманому прямокутнику подібний початковому. Це і є умовою того, що відношення сторін дорівнює золотому перерізу. Якщо знову відрізати квадрат, отримаємо прямокутник подібний даному.

.

ЗАСТОСУВАНЯ ЛАНЦЮГОВИХ ДРОБІВ ДЛЯ
РОЗВ’ЯЗУВАННЯ ЗАДАЧ

 Ланцюгові дроби є потужним інструментом  для розв’язування різного типу задач. Вперше ми зустрілися з поняттям ланцюгових дробів при підготовці до олімпіад, а саме розв’язуючі задачі Турніру імені Ломоносова.

 Задача 1.

 Довести, що виконується рівність:

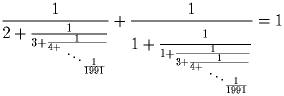
Розв’язання

Позначимо у правій частині заданої рівності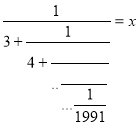   

Отримаємо вираз 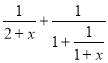, який і спробуємо перетворити, звівши до спільного знаменнику.

Отримаємо:

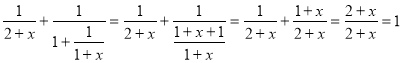, що і доводить нашу рівність.

Ланцюгові дроби використовуються для розв’язування діофантових рівнянь.

Задача 2.

Розв’язати у цілих числах рівняння

.

Розв’язання

 Розкладемо  у ланцюговий дріб:

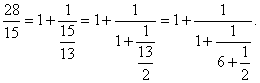
Передостаннє наближення – це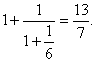  

Знайдемо різницю:

.

Звідси

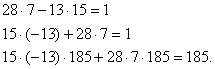
Отже

Замість t підставимо t+86. Тоді  

Відповідь: 

Наведемо приклад задачі з логістики, де нам вдалося використати діофантове рівняння та розв’язати його за допомогою ланцюгових дробів.

    Задача 3.

Для перевезення великої кількості контейнерів по170 кг та 190 кг виділені тритонні машини. Чи можна цими контейнерами завантажити машини повністю?

Розв’язання.

Позначивши через х та у кількість контейнерів по 170кг та 190кг відповідно, отримаємо після скорочення на 10 рівняння: 17х+19у=300 в цілих невід’ємних числах.
Як відомо, загальний розв’язок цього рівняння має вигляд:

де – будь-який частковий розв’язок рівняння. Тобто, задача полягає у знаходженні якогось часткового розв’язку.

Утворимо з коефіцієнтів рівняння неправильний дріб  і запишемо його у вигляді ланцюгового дробу:

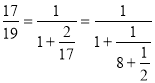
Передостаннє наближення цього ланцюгового дробу є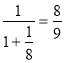 

Знайдемо різницю

Отже,

Отримали рівність, де в лівій частині стоїть вираз, схожий на ліву частину рівняння, але в правій частині заміть 300 стоїть 1. Помножимо обидві частини цієї рівності на 300:

Це означає, що є частковим розв’язком нашого рівняння. Отже, загальний розв’язок:

Знайдемо .

,  , 

Встановлюємо, що .

Отже, для оптимального використання вантажівок, що перевозять

по 3 т кожна, необхідно розташовувати контейнери так:

два по 170 кг та 14 по 190 кг.

Інколи ланцюгові дроби вдається використати у зовсім незвичних ситуаціях, як наприклад розв’язання задачі з фізики.

  Задача 4.

За допомогою довільної кількості одиничних опорів побудувати електричне коло , що має опір 10/7.

Розв’язання.

Використовуючи розклад звичайного дробу 10/7 у ланцюговий,

.

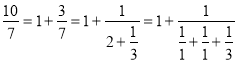 Потрібний опір можна отримати, з’єднавши послідовно 1 одиничний опір та блок, в якому у трьох паралельних лініях з’єднані 5 одиничних опорів так: 2 одиничних та блок з трьох послідовних одиничних опорів. Тоді опір другого блоку дорівнюватиме 3/7, а першого дорівнюватиме 1, що і вимагалось знайти.

ДЖЕРЕЛА, ЩО МОЖНА ВИКОРИСТАТИ ПРИ ВИВЧЕННІ ТЕМИ «ЛАНЦЮГОВІ ДРОБИ»

1.               Арнольд И.В.  Цепные дроби . -  М.: МЦНМО. - 2000. – С.13-14.
2.               Бугаєнко  В.О. Турниры им. Ломоносова. Конкурсы по математике. – М.:

          МЦНМО. – 1998.

3.               Виленкин Н.Я., Шибасов Л.П., Шибасова З.Ф. За страницами учебника

          математики .Арифметика. Алгебра. Геометрия. – М. Просвещение. – 1996.

4.               Устинов А. Цепные дроби вокруг нас // Квант. – 2010. - №2. – С.32-34.