Лекція "МЕТРОЛОГІЯ. МЕТРОЛОГІЧНА СЛУЖБА УКРАЇНИ."

ЛЕКЦІЯ

МЕТРОЛОГІЯ. МЕТРОЛОГІЧНА СЛУЖБА УКРАЇНИ.

Дисципліна: Основи стандартизації, метрології і сертифікації

Блок змістовних модулів: Метрологія. Метрологічна служба України.

Модульна одиниця: Метрологія

План лекції:

1 ПРЕДМЕТ І ЗМІСТ МЕТРОЛОГІЇ

2 ВИМІРЮВАННЯ ФІЗИЧНИХ ВЕЛИЧИН.

3 ПОХИБКИ ВИМІРЮВАНЬ.

4. ПОНЯТТЯ ЕТАЛОНА, ЗРАЗКОВИХ І РОБОЧИХ ЗАСОБІВ ВИМІРЮВАНЬ

 

1 ПРЕДМЕТ І ЗМІСТ МЕТРОЛОГІЇ

Предметом метрології є отримання кількісної і якісної інформації про властивості об’єктів і процесів, встановлення і застосування наукових і організаційних основ, технічних засобів, правил і норм, необхідних для досягнення єдності і необхідної точності.

Методи метрології - це сукупність фізичних і математичних методів, що використовуються для отримання вимірювальної інформації. До них належать: методи вимірювання, відтворення величин заданого розміру, порівняння величин, вимірювальне перетворення, обробка результатів спостережень, планування вимірювального експерименту.

Засоби метрології - різноманітні засоби вимірювань і контролю, які вдосконалюються і розвиваються на основі об’єктивних законів.

Збільшення числа структурних елементів, програмно-апаратна реалізація засобів вимірювання і контролю приводять до їх якісної зміни. Вони неперервно вдосконалюються – від найпростіших мір до приладів, установок, комп’ютерно-вимірювальних систем і метрологічних роботів.

Відбувається перехід кількості структурних елементів в нові якості.

Всі засоби вимірювання і контролю регламентуються державними і міжнародними правилами, законодавчими актами, що мають за мету підтримання єдності вимірювань і підвищення їх достовірності.

Таким чином, засоби метрології включають у себе:

 сукупність засобів вимірювання і контролю;

 систему державних еталонів одиниць фізичних величин;

систему передачі розмірів одиниць фізичних величин від еталонів усім засобам вимірювання за допомогою зразкових засобів повірки;

 систему обов’язкової державної і відомчої повірки, або метрологічної атестації засобів вимірювання;

 систему стандартних зразків складу і властивостей речовин, матеріалів.

Напрямки метрології. Усі розділи метрології розвиваються на основі об’єктивних законів, коли існуючі раніше засоби вимірювання відкидаються і замінюються новими, коли забезпечується єдність об’єкта дослідження і суб’єкта, їх взаємозв’язок і взаємодія приводить до підвищення точності.

Розвиваючись швидкими темпами, метрологія розподіляється на ряд самостійних розділів:

- теорія вимірювань;

- теорія похибок;

- інформаційна теорія вимірювань;

- теорія інформаційно-вимірювальних систем;

- статистичні вимірювання;

- вимірювання електричних величин;

- вимірювання магнітних величин;

- вимірювання неелектричних величин.

Факт існування в сучасній метрології різноманітних напрямків вивчення вимірювань є відображенням процесу диференціації науки про вимірювання як важливого принципу її розвитку.

Тенденція диференціації привела до створення окремих напрямків вимірювань, а також відповідних навчальних і наукових спеціальностей, що, в свою чергу, забезпечило їх прискорений розвиток. Однак поряд з тенденцією диференціації у зв’язку з розвитком наукових досліджень на межі різнорідних явищ, створенням складних систем з використанням фізичних явищ різного роду, ефективністю взаємного проникнення методів вимірювання і вимірювального перетворення з різних галузей науки і техніки посилюється тенденція інтеграції в розвитку метрології і вимірювальної техніки.

Напрямки розвитку метрології визначають її місце серед інших наук.

Метрологія веде до єднання різних наук. Вона тісно пов’язана з фундаментальними природничими науками, насамперед з технічною фізикою. Виконуючи завдання метрологічного забезпечення, вона поєднується і з суспільними науками, оскільки проблеми метрології мають багато спільного з типовими проблемами масового обслуговування.

2 ІСТОРИЧНІ ЕТАПИ РОЗВИТКУ МЕТРОЛОГІЇ

В 1832 р. К.Ф. Гаусом була розроблена система одиниць, яку він назвав абсолютною, з основними величинами - міліметр, міліграм, секунда. Основні величини запропонованої Гаусом системи відображають найзагальніші властивості матерії - масу і основні форми існування тобто простір і час. В зв'язку з цим її і подібні системи називали абсолютними, хоча це не зовсім відповідає дійсності тому що в кінці минулого віку В. Томсон запропонував систему побудовану на двох основних величинах L і T. Відомі системи з одною основною величиною, а також так звані природні систем одиниць, що базуються на універсальних фізичних константах.

В 1875 р. разом з підписанням Метричної конвенції було засноване Міжнародне бюро мір і ваг, МБМВ (фр. Bureau International des Poids et Mesures, BIPM ) - Постійно діюча міжнародна організація зі штаб-квартирою, розташованою в місті Севр (передмістя Парижа, Франція).

Основне завдання Бюро полягає в забезпеченні існування єдиної системи вимірювань у всіх країнах-учасницях цієї конвенції.

У МБМВ зберігаються міжнародні еталони основних одиниць і виконуються міжнародні метрологічні роботи, пов'язані з розробкою і зберіганням міжнародних еталонів і звіренням національних еталонів з міжнародними та між собою.

У МБМВ також проводяться дослідження в області метрології, спрямовані на збільшення точності вимірювань.

Повними одиницями системи Гауса були міліметр, міліграм і секунда, розміри яких незручні для практики. Тому в І88І р. Міжнародний конгрес електриків (МКЕ) прийняв систему одиниць СГС з основними одиницями - сантиметр, грам, секунда. Із трьох її різновидів електростатична СГСЕ, електромагнітна СГСМ .і симетрична СГС- остання ще й зараз має обмежене застосування в теоретичних розділах фізики і астрономії. Цей самий конгрес прийняв практичні електричні одиниці - см, вольт, ампер і фарад, а в 1889 р. II МКЕ - джоуль, ват і генрі.

В 1901 р. італійський інженер Джорджі запропонував систему МКС з основними одиницями - метр, кілограм, секунда - і показав, що на її основі можна побудувати когерентну практичну систему механічних і електричних одиниць, якщо за четверту основну одиницю взяти одну із практичних електричних одиниць. Був вибраний ампер і виникла когерентна практична система електромагнітних одиниць МКСА, а згодом система теплових одиниць МКСК з четвертою основною одиницею - кельвіном і система світлових одиниць МСК - метр, секунда, кандела. Всі ці системи когерентні і на їх основі побудована Міжнародна система одиниць SІ.

Залежно від форми запису рівнянь електромагнітного поля, які використовуються для утворення похідних одиниць, системи одиниць електричних і магнітних величин можуть бути нераціоналізовані і раціоналізовані. Раціоналізація цих рівнянь запропонована в кінці минулого сторіччя англійським фізиком Хевісайдом і полягає в тому, що множник 4π залишається тільки в рівняннях, пов'язаних з сферичною симетрією (закон Гауса, Кулона), а в більшості інших рівнянь відсутній. Тому за однакових розмірів основних одиниць розміри окремих похідних одиниць нераціоналізованої і раціоналізованої систем різні.

В 1960 р. XI Генеральна конференція з мір і ваги (ГКМВ) прийняла Міжнародну систему одиниць (Система інтернаціональна - SI) з основними одиницями - метр, кілограм, секунда, ампер, кельвін, кандела і з додатковими - радіан і стерадіан, а в 1971 р. ХІV ГКМВ затвердила сьому основну одиницю - моль.

В Україні з 01.01.1999 р. чинними є державні стандарти - ДСТУ 3561.0-97 Метрологія.

Одиниці фізичних величин. Основні одиниці фізичних величин Міжнародної системи одиниць.

Основні положення, назви та позначення, ДСТУ 3561.1-97 Метрологія. Одиниці фізичних величин. Похідні одиниці фізичних величин Міжнародної системи одиниць. Основні поняття, назви та позначення, ДСТУ 3561.2-97 Метрологія. Одиниці фізичних величин. Фізичні сталі та характеристичні числа. Основні положення, назви, позначення та значення, згідно з якими обов'язковим є застосування одиниць SI (табл. 1), а також часткових і кратних від них.

Метр є довжина шляху, який проходить світло у вакуумі за проміжок часу що дорівнює 1/299792458 секунди (ХVIІ ГКМВ. 1983 р.).

Кілограм дорівнює масі міжнародного прототипу кілограма (І ГКМВ, 1889 р.; ІІІ ГКМВ, 1901 р.)

Секунда дорівнює 9І9263І770 періодам випромінювання, яке відповідає переходові між двома надтонкими рівнями основного стану атома цезію-133 (ХIII ГКМВ, 1967 р.).

 

Таблиця 1. Основні і додаткові одиниці SI

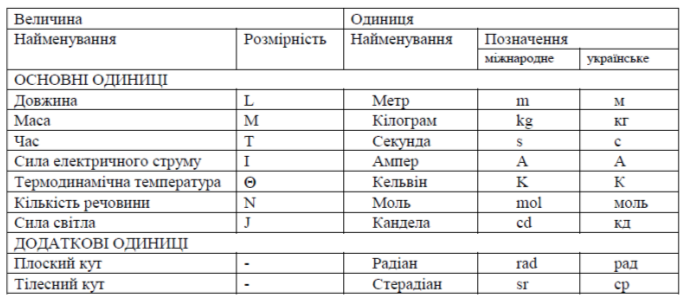
Ампер дорівнює силі незмінного струму, який при проходженні по двох паралельних прямолінійних проводах нескінченної довжини і знехтовно малої площі поперечного перерізу, розміщених на відстані 1 м один від одного у вакуумі, викликав би на кожній ділянці проводу довжини 1 м силу взаємодії 2∙10^-7 Н (IX ГКМВ, 1948 р.).

Кельвін дорівнює 1/273,16 частині термодинамічної температури потрійної точки води (ХІІІ ГКМВ, І967 р.).

Моль дорівнює кількості речовини системи, яка вміщує стільки ж структурних елементів, скільки міститься атомів у вуглеці-12 масою 0,012 кг. При застосуванні моля структурні елементи мають бути специфіковані і можуть бути атомами, молекулами, іонами, електронами та іншими частинками або специфікованими групами частинок (ХІV ГКМВ, 1971 р.).

Кандела дорівнює силі світла в заданому напрямі джерела, що випускає монохроматичне випромінювання частотою 540∙10¹² Гц, енергетична сила світла якого в цьому напрямі становить 1/683 Вт/ср (ХVІ ГКМВ, 1979 р.).

Радіан дорівнює куту між двома радіусами кола, дуга між якими дорівнює радіусу.

Стерадіан дорівнює тілесному куту з вершиною в центрі сфери, який вирізає на поверхні сфери площу, що дорівнює площі квадрата зі стороною, яка дорівнює радіусу сфери.

Система одиниць SI - практична, когерентна, раціоналізована. В ній, на відміну від нераціоналізованої системи СГС, магнітна проникність μо вільного простору – величина розмірна і називається магнітною сталою:

μо = 4π∙10^-7≈12,57^-7 Гн/м;

подібно електрична стала

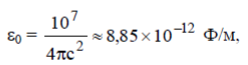
де С = (299792,5±0,4) км/с - швидкість поширення світла у вільному просторі.

 

Практичні рекомендації з правильного застосування елементів системи SI

Треба користуватися термінами "маса" і "густина", а не "вага" i "питома вага", кількість теплоти виражати в джоулях, а не в калоріях. Крім температури Кельвіна (позначення Т), допускається застосування також температури Цельcія (позначення t), яка визначається як t = Т - Т₀ = T - 273,15 і виражається в градусах Цельсія °С. Інтервал або різницю температур Кельвіна виражають в Кельвінах (К), а інтервал або різницю температур Цельсія дозволяється виражати як в Кельвінах, так і в градусах Цельcія.

Одиниці SІ позначаються літерами латинського і грецького (міжнародні позначення) або українського алфавітів, а також спеціальними знаками (...° ;...' ;..."). На засобах вимірювань мають бути міжнародні позначення. В друкованих виданнях можна застосовувати міжнародні або українські позначення, але не обидва види в одному виданні, за винятком публікацій з фізичних величин.

В позначеннях одиниць, назви яких походять від прізвищ, перша буква має бути велика, наприклад, А, А; W, Вт; Wb, Вб; Ω, Ом. Позначення одиниць проставляються тільки післячислових значень величин в один рядок з ними, друкуються прямим шрифтом з пробілом після останньої цифри і без перенесення в наступний рядок. Наприклад, 100 кВт, 80%, 20 °С, але 20°, 30'.

Значення величин і їх граничні відхилення беруться в дужки, після яких з пробілом проставляється позначення одиниці, наприклад, (100,0 ± 0,1) В або ж окремо - після значення величини і після її граничного відхилення: 50,0 В ± 0,2 В,

Позначення одиниць, що входять в добуток, треба відділяти крапкою на середній лінії (знак множення): Н∙м, кг∙м².

В позначеннях відношень одиниць знаком ділення може служити тільки одна скісна або горизонтальна риска. Позначення зі скісною рискою записують в один рядок, а знаменник - добуток беруть у круглі дужки. Дозволяється позначення відношень одиниць записувати у вигляді добутку позначень одиниць, піднесених до додатних чи від'ємних степенів, але якщо для однієї з одиниць, що входять у відношення, установлено позначення у вигляді від'ємного степеня, то застосовувати скісну чи горизонтальну риску не дозволяється.

 

2 ВИМІРЮВАННЯ ФІЗИЧНИХ ВЕЛИЧИН.

2.1 Основні терміни в галузі метрології

Метрологія - наука про вимірювання, методи і засоби забезпечення їх єдності та способи досягнення потрібної точності.

Вимірювання - знаходження значень фізичних величин експериментальним шляхом.

Фізична величина - будь-яка властивість матеріального об'єкту, яку можна кількісно визначити.

Єдність вимірювань - такий стан вимірювань коли фізичні величини виражені в узаконених одиницях, а значення їх похибок відомі з заданою імовірністю.

Метрологія поділяється на теоретичну, прикладну і законодавчу:

- теоретична - вирішує загальні наукові проблеми вимірювань;

- предметом прикладної метрології є практичне застосування положень теоретичної метрології;

- законодавча - полягає у встановленні та контролі за дотриманням спеціальних вимог і правил для забезпечення єдності і потрібної точності вимірювань.

Названі три розділи є взаємопов'язані і мають на меті вирішення ряду завдань, найважливіші серед яких є:

- опрацювання загальної теорії вимірювань;

- розробка теорії певних окремих видів вимірювань;

- розробка теорії фізичних величин, одиниць і систем фізичних величин;

- розробка теорії похибок;

- визначення фізичних констант і стандартних довідкових даних про властивості речовин і матеріалів;

- розробка еталонів і стандартних зразків;

- розробка засобів вимірювання;

- забезпечення правильної експлуатації засобів вимірювальної техніки;

- відтворення розмірів одиниць з допомогою еталонів і передавання їх усім іншим засобам вимірювання;

- нормування метрологічних характеристик засобів вимірювання;

- нормування стандартних вимірювальних процесів і методик виконання вимірювань;

- метрологічний нагляд за засобами вимірювання і правильністю їх застосування.

Порівнюючи окремі завдання можна розрізнити, які з них більше чи менше відповідають окремим трьом розділам метрології, але ніколи їх не можна віднести тільки до одного з них.

Однак треба зазначити, що функції прикладної і законодавчої метрологій завжди підпорядковані положенням теоретичної. В свою чергу, положення теоретичної метрології знаходять практичну перевірку при реалізації функцій прикладної та законодавчої метрологій.

Метрологія оперує рядом термінів, що встановлені ДСТУ 2681-94 «Метрологія. Терміни та визначення». Цей стандарт встановлює обов'язкові для використання терміни у всіх видах нормативної документації, науково-технічній, навчально-методичній літературі, що належить до метрології та метрологічного забезпечення, а також робіт зі стандартизації або при використанні результатів цих робіт, включаючи програмні засоби для комп'ютерних систем.

Наведемо характеристику найбільш уживаних з стандартизованих термінів:

фізична величина - властивість, спільна в якісному відношенні для багатьох матеріальних об'єктів та індивідуальна в кількісному відношенні для кожного з них;

розмір (фізичної) величини - кількісний вміст фізичної величини в даному об'єкті;

значення (фізичної) величини - відображення фізичної величини у вигляді числового значення величини із позначенням її одиниці;

істинне значення (фізичної величини) - значення фізичної величини, яке ідеально відображало б певну властивість об'єкта;

умовно істинне значення (фізичної величини) - значення фізичної величини, знайдене експериментальним шляхом і настільки наближене до істинного значення, що його можна використати замість істинного для даної мети (дійсне значення);

система (фізичних) величин - сукупність взаємопов'язаних фізичних величин, в якій декілька величин приймають за незалежні, а інші визначають як залежні від них;

основна (фізична) величина - фізична величина, що входить до системи фізичних величин і прийнята за незалежну від інших величин цієї системи;

похідна (фізична) величина - фізична величина, що входить до системи величин та визначається через основні величини цієї системи;

розмірність фізичної величини - вираз, що відображає її зв'язок із основними величинами системи;

одиниця (фізичної) величини - фізична величина певного розміру, прийнята за угодою для кількісного відображення однорідних з нею величин;

числове значення (фізичної) величини - число, що дорівнює відношенню розміру фізичної величини, що вимірюється, до розміру одиниці цієї фізичної величини чи кратної одиниці;

вимірювання - відображення вимірюваних величин їх значеннями шляхом експерименту та обчислень за допомогою спеціальних технічних засобів;

пряме вимірювання - вимірювання однієї величини, значення якої знаходять безпосередньо без перетворення її роду та використання відомих залежностей;

непряме вимірювання - вимірювання, у якому значення однієї чи кількох вимірюваних величин знаходять після перетворення ряду величини чи обчислення за відомими залежностями їх від декількох величин аргументів, що вимірюються прямо;

опосередковане вимірювання - непряме вимірювання однієї величини з перетворенням її роду чи обчисленнями за результатами вимірювань інших величин, з якими вимірювана величина пов'язана явною функціональною залежністю;

сукупне вимірювання - непряме вимірювання, у якому значення кількох одночасно вимірюваних однорідних величин отримують розв'язанням рівнянь, що пов'язують різне сполучення цих величин, які вимірюються прямо чи опосередковано;

сумісне вимірювання - непряме вимірювання, у якому значення кількох одночасно вимірюваних різнорідних величин отримують розв'язанням рівнянь, які пов'язують їх з іншими величинами, що вимірюються прямо чи опосередковано;

абсолютна похибка (вимірювання) - різниця між результатом вимірювання та умовно істинним значенням вимірюваної величини ;

відносна похибка - відношення абсолютної похибки вимірювання до умовно істинного значення вимірюваної величини;

систематична похибка (вимірювання [засобу вимірювальної техніки]) - складова похибки, що залишається сталою або прогнозовано змінюється у ряді вимірювань тієї самої величини;

випадкова похибка (вимірювання [засобу вимірювальної техніки]) - складова похибки, що непрогнозовано змінюється в ряді вимірювань тієї самої величини;

методична похибка (вимірювання) - складова похибки вимірювання, що зумовлена неадекватністю об'єкта вимірювання та його моделі, принятої при вимірюванні;

інструментальна похибка (вимірювання) - складова похибки вимірювання, зумовлена властивостями засобів вимірювальної техніки;

точність вимірювання - головна характеристика якості вимірювання, що відображає близькість результату вимірювання до істинного значення вимірюваної величини;

засіб вимірювальної техніки - технічний засіб, що застосовується під час вимірювань і має нормовані метрологічні характеристики;

міра (величини) - вимірювальний пристрій, що реалізує відтворення й збереження фізичної величини за, даного значення;

вимірювальний прилад - засіб вимірювань, у якому створюється візуальний сигнал вимірювальної інформації;

метрологічні характеристики - характеристики засобів вимірювань, що нормуються для визначення результату вимірювання та його похибок;

клас точності (засобу вимірювальної техніки [засобу вимірювань]) – узагальнена характеристика засобу вимірювань, що визначається межами його допустимих основної і додаткових похибок, а також іншими характеристиками, що впливають на його точність;

еталон (одиниці фізичної величини) - засіб вимірювальної техніки, що забезпечує відтворення й збереження одиниці фізичної величини та передавання її розміру відповідним засобам, що стоять нижче за повірочною схемою, офіційно затверджений як еталон;

первинний еталон - еталон, що забезпечує відтворення й зберігання одиниці фізичної величини з найвищою в країні (у порівнянні з іншими еталонами) точністю;

робочий еталон - еталон, призначений для передавання розміру фізичної величини засобам вимірювальної техніки;

метрологічна служба - мережа організацій, окрема організація або окремий підрозділ, на які покладена відповідальність за забезпечення єдності вимірювань у закріпленій за ними сфері діяльності;

метрологічне забезпечення - встановлення й застосування метрологічних норм і правил, а також розроблення, виготовлення та застосування технічних засобів, необхідних для забезпечення єдності й потрібної точності вимірювань;

повірка засобів вимірювальної техніки - визначення похибок засобів вимірювальної техніки та встановлення придатності їх до застосування.

Усі матеріали наступних питань базуються на правильному розумінні термінів. Тому в тих місцях, де описані терміни часто вживаються, в контексті питання повторюється їх визначення, що дає змогу швидко зорієнтуватися та зберегти цілісність викладеного матеріалу.

2.2 Види фізичних величин

Фізична величина (ФВ) це кожна (одна з багатьох) означена якісно властивість фізичних об'єктів (фізичних тіл, їх систем, станів, процесів), яка може мати певний розмір. Приклади ФВ: довжина, маса, швидкість, сила електричного струму, світловий потік. Розмір ФВ є її атрибутом, що існує об'єктивно, незалежно від наших знань про нього. За характером зв'язків розмірів ФВ з об'єктами, яким вони притаманні, їх поділяють на екстенсивні та інтенсивні величини.

Екстенсивні ФВ (маса, довжина, площа, енергія та ін.) при поділі об'єкта на частини змінюють свої розміри і є аддитивними величинами, тобто їх можна додавати або віднімати.

Інтенсивна величина характеризує стан фізичного об'єкту і при його поділі на частини може зберігати свій розмір, наприклад, густина, температура питомий електричний опір.

Інтенсивні ФВ не є аддитивними (густина суміші не дорівнює сумі густини компонентів).

За характером виявлення ФВ поділяються на енергетичні (активні), які здатні самі проявляти свої розміри (температура, напруга) і параметричні (пасивні), опір, індуктивність, ємність, розміри яких проявляються при впливі на об'єкт відповідної активної величини (відповідно активні та пасивні величини визначаються з використанням різних видів вимірювань - прямих та непрямих).

Конкретні ФВ існують в просторі і часі, перебувають в причинно-наслідкових зв'язках з іншими ФВ згідно з законами фізики. Тому розміри ФВ є функціями часу, координат та інших величин.

Розрізняють скалярні і векторні величини. Скалярні - відповідно поділяються на неполярні, що мають тільки розмір (маса, об'єм), і полярні, які мають ще й знак (заряд, напруга).

Векторні ФВ (сила, переміщення, швидкість) поруч з розміром мають напрям і отримуються як зміна іншої ФВ в просторі і часі (переміщення - зміна координати в просторі, швидкість – зміна переміщення в часі), а математично описуються похідними.

Розміри ФВ можуть змінюватись неперервно або стрибкоподібно (дискретно). ФВ, розмір якої виражений як функція часу, за визначенням, становить процес, тобто послідовну в часі зміну розміру величини.

2.2 Одиниці фізичних величин

Позначимо всі можливі розміри ФВ через X, тобто X - множина розмірів ФВ. Візьмемо серед них довільний розмір X0 і назвемо його розміром одиниці величини X. Тоді відношення X/X₀=M буде певним числовим значенням величини Х і кожний можливий її розмір можна виразити через якесь числове значення. Отже, одиниця ФВ - такий її розмір, якому присвоєно числове значення, що дорівнює 1.

Вимірюванням замість числа М знаходять наближене його значення N, через яке отри- мують наближене значення ФВ - х=NX₀, яке є тільки оцінкою істинного значення величини.

Значення ФВ, яке настільки близьке до істинного її значення, що для даної цілі може бути використане замість істинного, називають дійсним значенням: хД=NдХ₀.

ФВ пов'язані поміж собою залежностями, які виражають одні величини через інші.

Сукупність пов'язаних такими залежностями величин, серед яких одні умовно вважаються незалежними, а інші виражаються через них, називають системою величин. В системі незалежні величини називаються основними, всі решта - похідними величинами.

Сукупність основних і похідних одиниць певної системи величин становить систему їх одиниць. В побудові системи одиниць вибір основних величин і розмірів їх одиниць теоретично довільний, але практично є продиктований певними раціональними вимогами:

- число основних величин має бути невелике;

- за одиниці мають бути вибрані величини, одиниці яких легко відтворити з високою точністю;

- розміри основних одиниць мають бути такі, щоби на практиці значення всіх величин системи не виражалися ні надто малими, ні надто великими числами;

- похідні одиниці мають бути когерентні, тобто входити в рівняння, що пов'язують їх з іншими одиницями системи, з коефіцієнтом 1.

Одиниці, що не належать ні до основних, ні до похідних одиниць даної системи, називають додатковими. Одиниці, що не входять в жодну з систем, називають позасистемними (літр - l, тонна - t; градус - 0 та ін.). До позасистемних одиниць належать також відносні одиниці: процент (відсоток) - о/о; промілле - о/оо; мільйонна частина - ppm (млн^-1), а також одиниці що визначаються з відношення двох значень величини - логарифмічні одиниці: бел - В, децибел -dB; октава - окт; декада - дек; фон - phon.

Одиниця, що в ціле число разів більша за системну називається кратною, а - менша за системну називається частковою. Для їх утворення використовують спеціальні префікси: екса-, пета-, фемто-, атто- та ін. Одиниці, від яких утворились кратні або часткові одиниці, називаються головними.

2.3  Класифікація вимірювань

Види вимірювань

Повної сталої і загальновизнаної класифікації вимірювань немає. Практично використовують певний варіант неповної класифікації, який відповідає призначенню.

Розглянемо декілька прикладів класифікацій вимірювань за певними ознаками:

- за наявністю розмірності – розмірні, безрозмірні;

- за наявністю попереднього вимірювального перетворення – безпосередні (вимірювана величина (ВВ) вимірюється без будь-яких попередніх перетворень шляхом порівняння з величиною міри), з попереднім перетворенням (ВВ попередньо перетворюється у величину, однорідну з величиною міри, після чого відбувається порівняння)

- за співвідношенням між числом n вимірюваних величин і числом m рівнянь вимірювань (n<m, n=m, n>m);

- за способом здійснення умови m>n (повторне вимірювання m раз, m-канальне вимірювання ).

Однією з найбільш поширених ознак, за якою визначають види вимірювань - прямі, непрямі (опосередковані, сукупні та сумісні), - є характер співвідношень, на підставі яких знаходять значення вимірюваних величин.

Вимірювання пряме, якщо значення вимірюваної величини знаходять безпосередньо з дослідних даних, наприклад, вимірювання довжини лінійкою з поділками, потужності - ватметром. На противагу прямим - опосередковані, сукупні та сумісні вимірювання називають непрямими.

Опосередкованим називають вимірювання (n=1) однієї величини X, значення якої x знаходять за результатами u, v, ..., w, прямих вимірювань величин U, V, ..., W, з якими величина Х пов'язана явною функціональною залежністю X=F(U, V, ..., W).

Наприклад, питомий електричний опір

заходять за значеннями опосередкованих вимірювань опору R, довжини l і діаметру d провідника з круглим перерізом; значення потужності P=UI постійного струму або опру R=U/I знаходять за результатами прямих вимірювань напруги U вольтметром і сили струму I амперметром.

Опосередковані вимірювання виконують тоді, коли значення величини неможливо або складно виміряти прямо або якщо вони забезпечують вищу точність, ніж прямі.

Сумісними називають вимірювання n ≥ 2 неоднойменних величин U, V, ..., Z, значення яких u, v, ..., z знаходять за результатами x_і1, x_і2, ..., x_іn прямих або опосередкованих вимірювань величин X_і1, X_і2, ..., X_іn, через які величини U, V, ..., Z, пов’язані між собою системою m- умовних (емпіричних) рівнянь

Fi (U, V, ..., Z; X_і1, X_і2, ..., X_іn)=0

і=1,2, ..., m, причому m ≥ n

Прикладом сумісних вимірювань може також бути визначення температурних коефіцієнтів опору за результатами прямих вимірювань опору резистора і його температури. Сумісні вимірювання використовуються також для визначення функціональних залежностей міх величинами.

Наприклад, відомо, що індуктивність котушки L=L₀(1+ω²CL₀), де L₀ – індуктивність на частоті ω=2πf→0; C – міжвиткова ємність.

Значення C і L₀ не можна знайти прямими або опосередкованими вимірюваннями. Тому в найпростішому випадку, коли m=2, вимірюють індуктивність котушки L₁=X₁₁ при ω₁=X₁₂ і L₂=X₂₁ при ω²=X₂₂ і складають систему рівнянь

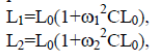
розв’язуючи яку, знаходять C і L₀

Сукупними називають вимірювання n ≥ 2 однойменних величин X₁, Х₂, ..., Х_n, значення яких х₁, х₂, ..., х_n знаходять за результатами х_і1, х_і2, ..., х_іn прямих вимірювань величин X_і1, Х_і2,..., Х_іn, які є комбінаціями величин X₁, Х₂, ..., Х_n, і пов’язані з ними системою m-умовних рівнянь

F_i (X₁, Х₂, ..., Х_n; X_і1, Х_і2, ..., Х_іn)=0

і=1,2, ..., m, причому m ≥ n

Наприклад, щоб знайти значення r₁, r₂, r₃ опорів R₁, R₂, R₃ резисторів, що сполучені трикутником, вимірюють опори R₁₂, R₂₃, і R₃₁ на кожній парі вершин трикутника і, якщо m=n, отримують системи рівнянь, що пов’язують значення опорів. Розв’язуючи систему 3-х рівнянь, знаходять значення опорів r₁, r₂, r₃.

Для підвищення точності сумісних і сукупних вимірювань, забезпечують умову m > n і систему несумісних умовних рівнянь розв'язують, застосовуючи метод найменших квадратів.

2.4 Абсолютні і відносні, аналогові і цифрові, звичайні та статистичні вимірювання

Згідно з стандартом ДСТУ 2681-94 вимірювання називається абсолютним, якщо воно базується на прямих вимірюваннях однієї або декількох основних величин і використанні значень фізичних констант, а відносним - вимірювання відношення величини до однойменної, яка відіграє роль одиниці, або вимірювання зміни величини по відношенню до однойменної, що взята за початкову.

Ознакою поділу вимірювань на аналогові і цифрові служить форма вимірювальної інформації, яку несе інформативний параметр вихідного сигналу засобу вимірювань. Результат вимірювань завжди має цифрову форму, але операції квантування і цифрового кодування в аналогових вимірюваннях виконує людина, а в цифрових вони здійснюються автоматично.

Ознакою поділу вимірювань на звичайні і статистичні служить відповідно відсутність і наявність статистичної обробки результатів спостережень. Всі вимірювання (прямі і непрямі) з однократними (одноразовим) спостереженнями - звичайні, а з багатократними (багаторазовим)- статистичні. Вимірювання з багаторазовими спостереженнями називають рівноточними, якщо вимірювана величина і умови вимірювань незмінні, а засоби вимірювань і експериментатор ті самі; якщо ж хоча б одна з цих умов не виконується, то вимірювання вже будуть нерівноточними.

2.5 Класифікація методів вимірювань

З визначення поняття вимірювання випливає, що неодмінною його операцією є порівняння інформації про розміри величин. Згідно з ДСТУ 2681-94 метод вимірювання – сукупність способів використання засобів вимірювальної техніки та принципу вимірювань для створення вимірювальної інформації; розрізняють 6 методів:

1 - метод зіставлення (Messmethode mit direktem Vergleich)- метод прямого вимірювання з одноразовим порівнянням вимірюваної величини з усіма вихідними величинами багатозначної нерегульованої міри. Приклади 1. Вимірювання довжини лінійкою з поділками. 2. Вимірювання інтервалу часу годинником.

2 - метод одного збігу (метод ноніуса) - метод прямого вимірювання з одноразовим порівнянням вихідних величин двох багатозначних нерегульованих мір, з різними за значеннями ступенями, нульові позначки яких зсунуті між собою на вимірювану величину.

Приклади 1. Вимірювання довжини за допомогою двох лінійок з поділками, ціни яких знаходяться в певному відношенні (штангенциркуль). 2. Вимірювання часу за допомогою двох послідовностей періодичних імпульсів, періоди яких знаходяться в певному відомому відношенні.

Метод збігу полягає в тому, що різниця міх ефектами, які викликані діяннями вимірюваної і зразкової величини, визначається за збігом шкал або періодичних сигналів. (Приклади: вимірювання довжини штангенциркулем з ноніусом та частоти стробоскопом).

3- метод подвійного збігу (метод коінциденції, Koinzidenzmessmethode) - метод прямого вимірювання з одноразовим порівнянням двох квантованих фізичних величин: вимірюваної та відтворюваної багатозначною нерегульованою мірою. Приклади 1. Вимірювання зістикованих інтервалів часу за допомогою послідовності періодичних імпульсів з відомим значенням їх періоду. 2. Вимірювання зістикованих відрізків довжини за допомогою лінійки з відомим значенням поділок.

4 - метод зрівноваження з регульованою мірою (Nullmessmethode) - метод прямого вимірювання з багаторазовим порівнянням вимірюваної величини та величини, що відтворюється мірою, яка регулюється, до їх повного зрівноваження. Приклад Вимірювання електричної напруги компенсатором; зважування на рівноплечих терезах (метод протиставлення).

Цей метод ще має назву - нульовий метод вимірювання, бо відрізняється тим, що результуючий ефект діяння вимірюваної Х і зразкової XЗ величин на пристрій порівняння доводять до нуля.

5 - диференційний метод (різницевий метод, Differentielle Messung) - метод вимірювання, за яким невелика різниця між вимірюваною величиною та вихідною величиною одноканальної міри вимірюється відповідним засобом вимірювання.

Диференціальний метод вимірювань полягає в тому, що на вимірювальний прилад діє різниця вимірюваної Х і зразкової Х_З величин, тобто ∆Х = Х - Х_З<<X_З, а результат вимірювання визначається як х = Х_З + ∆Х, причому похибка вимірювання величини Х визначається практично похибкою відтворення зразкової величини X_З.

6 - метод заміщення (Substitutions-Messmethode) - метод непрямого вимірювання з багаторазовим порівнянням до повного зрівноваження вихідних величин вимірювального перетворювача з почерговим перетворенням ним вимірюваної величини та вихідної величини регульованої міри (метод сравнения с мерой, в котором измеряемую величину замещают известной величиной, воспроизводимой мерой).

Метод заміщення - метод вимірювань, при якому ефект діяння вимірюваної величини на пристрій порівняння (компаратор, вимірювальний прилад) запам'ятовується, а потім відновлюється діянням на нього зразкової величини. Приклад - вимірювання опору неточною мостовою схемою з застосуванням заміщуючого магазина опору.

З визначень диференціального і нульового методів вимірювань випливає, що вони є окремими випадками інших методів порівняння з мірою, причому кожний з них визначається ступенем повноти реалізації цих методів. Нульовий метод має місце при повній компенсації, повному протиставленні, заміщенні чи збігу (в межах можливостей компаратора), а диференціальний - при неповній реалізації цих методів.

Компенсаційний метод вимірювань полягав в тому, що на вході пристрою порівняння (компаратора) одночасно діють дві величини - полярна або векторна вимірювана і такої ж фізичної природи зразкова величина, розмір якої відтворюється мірою, а співвідношення між їх розмірами визначається за вихідним сигналом пристрою порівняння. Приклад – вимірювання напруги постійного струну за допомогою компенсатора шляхом її порівняння з ЕРС нормального елемента.

 

3 ПОХИБКИ ВИМІРЮВАНЬ.

3.1 Поняття результату і похибки вимірювання. Класифікація похибок

Експериментатор, виконуючи операції процесу вимірювань, одержує результати спостережень про значення вимірюваної величини, які називають результатами спостережень при вимірюваннях. Вони можуть бути однократними (одноразовими) або многократними (багаторазовими). Результати спостережень при вимірюваннях ще не є результатами вимірювань.

Результат вимірювання, як значення величини, що знайдене шляхом її вимірювання, одержують після відповідної обробки результатів спостережень, на основі якої визначають кількісні показники точності і вибирають форму подання результату вимірювання згідно з відповідними державними стандартами. У випадку однократного спостереження результат вимірювання знаходять, оцінюючи за відомими метрологічними характеристиками засобів вимірювань границі, в яких за даних умов із заданою ймовірністю може бути значення похибки вимірювання і подають результат у належній стандартній формі.

Класична метрологія виходить з позиції, що результат вимірювання завжди відрізняється від істинного значення вимірювання величини.

Згідно з стандартом під істинним значенням ФВ, розуміють таке її значення, яке ідеально відображає в якісному і кількісному відношенні певну властивість об’єкту. Але через обмежені можливості вимірювання істинне значення ФВ залишається невідомим, тому на практиці замість нього використовують поняття дійсного значення.

Під дійсним значенням ФВ розуміють значення, знайдене експериментально засобами вимірювання високої точності і їх покази можуть бути використані замість істинних.

Похибка вимірювань – це відхилення результату вимірювання від істинного значення (дійсного). Тому, перш за все можна говорити про абсолютну похибку вимірювань, яка визначається за формулою:

Ця похибка визначається в одиницях вимірювання величини.

Наприклад:

Тому для того щоб виключити похибку, необхідно в результат вимірювання внести поправку, тобто абсолютну похибку з протилежним знаком.

Мета вимірювання – одержання достовірної інформації, точність. Але тільки по значенню абсолютної похибки неможливо судити про точність вимірювання. Більшу інформацію про точність дає відносна похибка.

Відносна похибка – відношення абсолютної похибки до дійсного значення вимірюваної величини. Вона може виражатися як у відносних величинах так і у відсотках.

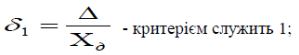
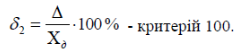
Із сказаного можна зробити висновок, що за способами вираження похибки поділяються на абсолютні і відносні.

Кількісно точність θ вимірювання визначається як величина обернена до відносної похибки

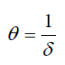
Для загальної характеристики точності самого приладу користуються зведеною похибкою,яку позначають шклом на шкалі приладу, або вказують в паспорті цього приладу.

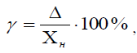
де Х_н - нормоване значення, в залежності від відлікового пристрою воно може приймати такі значення.

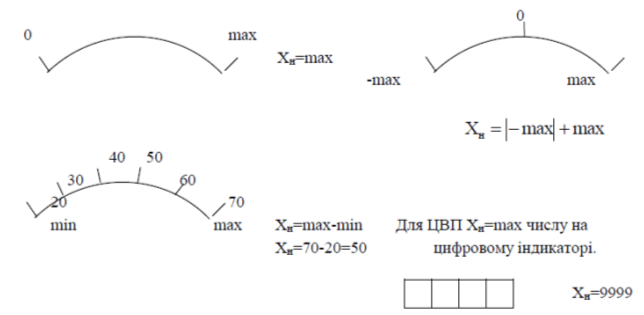
Клас точності – це максимально зведена похибка, яку гарантує підприємство виробник.

Цю похибку визначають у кожній оцифрованій точці шкали. Про клас точності судять по максимальній зведеній похибці. Вказують клас точності на приладі відповідним числом 0,5; 1,0; 1,5 і т. д. По ДСТУ 8,401-80

6; 4; 2,5; 1,5; 1,0; 0,5; 0,2; 0,1; 0,05; 0,02; 0,01; 0,005; 0,002; 0,002.

Якщо клас точності вказано у вигляді дробу 0.01/ 0.02, це означає, що зведена похибка в кінці вимірювати ± 0.02%, а на початку ± 0.01%

Задача. При повірці амперметра з верхньою межею вимірювання 5 А в точках шкали 1,2,3,4,5 А одержали відповідно значення зразкового приладу 0,95; 2,07; 1,045; 40,6; 4,95 А.

Необхідно побудувати криву поправок та визначити до якого класу точності можна віднести амперметр по результатам повірки.

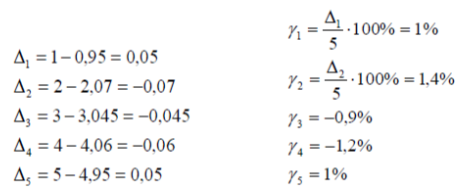
При вимірюванні однієї і тієї ж величини можна побачити, що в одних випадках похибка залишається постійною, в інших зростає або спадає на одну і ту ж величину, або змінюється випадковим чином, незалежно від нас.

Тому за характером зміни виділяють дві складових похибки: систематичну і випадкову.

Систематична похибка ∆ -- це складова похибки вимірювань, яка при повторних вимірювань однієї і тієї ж величини залишається постійною або змінюється за відомим законом, який може бути експериментально встановлений.

Випадкова похибка ∆ - це складова похибки вимірювань, яка при повторних вимірювань однієї і тієї ж величини змінюється випадковим чином.

Крім цих похибок в процесі вимірювання можуть виникати грубі похибки, тобто такі, які суттєво відрізняються від інших. Вони можуть виникати при помилках чи неправильних діях оператора (його стану, неправильного включення приладу, обчислення) або різній зміні умов проведення вимірювань (вібрації, надходження холодного повітря). Ці похибки при обробці результатів відкидаються.

За місцем виникнення похибки вимірювання розподіляються на інструментальні та методичні.

Інструментальні похибки виникають через недосконалість ЗВ:

- похибки градуювання або невеликий зсув шкали;

- зміна параметрів деталей і механізмів приладів в часі:

- неінформативних параметрів вхідних сигналів (частоти та ін.)

Методичні похибки виникають через недосконалість виду вимірювань: сукупні або сумісні.

3.2 Систематичні похибки

1. Залежно від причини виникнення систематичні похибки діляться на чотири групи:

- інструментальні – обумовлені конструктивною або технологічною недосконалістю ЗВ (градування шкали, вимірювальних перетворювачів (шунтів або додаткових опорів), стабільності параметрів деталей і т. п.);

- похибки встановлення – виникають в результаті відхилення від нормальних умов роботи для даного ЗВ (відхилення температури від нормальної, наявність зовнішніх полів);

- методичні похибки – виникають через недоліки самого методу вимірювання, використання спрощених формул.

Наприклад: 1) При вимірюванні опору на схемах амперметра-вольтметра;

2) При вимірюванні розподілу напруги у високоомному електричному колі низькоомним вольтметром

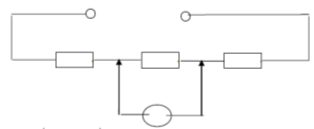
при підключенні такого вольтметра спад напруги на резисторі R2 понизиться і буде неправильний результат.

3) Для платини більш точна формула:

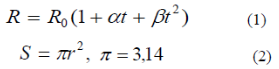
- суб’эктивні похибки – виникають від недосконалості органів чуств спостерігача, недостатній досвід, неуважність при підрахунку.

2. За характером зміни в часі: постійні, прогресивні і періодичні.

- постійні – які є незмінними протягом всіх вимірювань

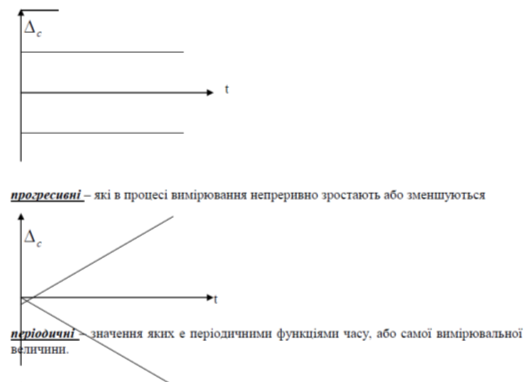
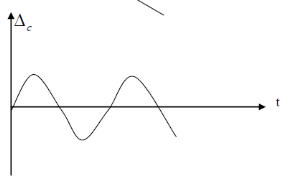
3.3 Методи усунення систематичних помилок

1) Введення поправок

При введенні поправок рівняння вимірювань набуває вигляду X=X+∆X+∆q , Якщо ∆X = -∆q , то систематична похибка виключається. При перевірці приладів на кожну поділку шкали визначають поправку. Будують криву поправок.

2) Дворазове вимірювання: якщо джерело систематичної похибки має направлену дію, то можна її компенсувати, провівши два експерименти так, щоб систематична похибка увійшла в другий результат вимірювання з протилежним знаком

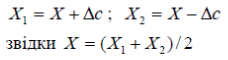
3) Рандомізація (від англійського - пермішування)

Наприклад: інструментальна похибка окремого приладу є систематичною у всіх випадках використання цього приладу. При виготовленні партії таких приладів похибка вже є випадковою. І якщо почергово вимірювати одну і ту ж величину такими приладами, то систематична похибка перейде у випадкову. І якщо в результаті обчислити середня значення, то воно буде найбільш наближене до дійсного значення.

Наприклад: вимірювання ваги на рівноплечих ричажних вагах вантах порівнюється з масою гир два рази: один раз будучи розміщеним на одній шпильці ваг, а другий раз – на іншій.

В цьому випадку похибка із-за нерівноплечості ваг ввійде з протилежним знаком. Результат буде вільним від похибки. Нехай  ℓ₁i  ℓ₂- довжини речагів ваг.

 

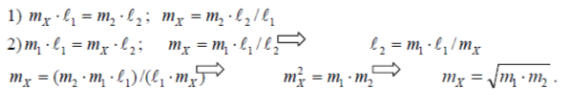
4. ПОНЯТТЯ ЕТАЛОНА, ЗРАЗКОВИХ І РОБОЧИХ ЗАСОБІВ ВИМІРЮВАНЬ

Результати вимірювань мають виражатися в узаконених одиницях і з потрібною точністю.

За рівних інших умов точність вимірювань визначається метрологічними характеристиками використовуваних 3В. Тому всі 3В підлягають обов'язковій повірці (верифікації, перевірці) або калібруванню. Повірка 3В полягав в офіційному ствердженні їх придатності для застосування за призначенням. Висновок робиться на підставі результатів контролю характеристик ЗВ, в основному метрологічних, на відповідність вимогам НТД. Ієрархічно 3В поділяються на еталони і робочі 3В.

Еталон (еталон одиниці) - 3В (або комплекс 3В), що забезпечує відтворення і (або) зберігання одиниці з метою передачі її розміру тим 3В, що стоять нижче за схемою перевірки, і офіційно затверджений в установленому порядку як еталон (наприклад, комплекс 3В для відтворення метра черев швидкість поширення світла у вакуумі, затверджений як державний еталон метра).

Робочими називаються ті 3В, що використовуються для виконання всіляких вимірювань в державному господарстві, але не служать для перевірки інших 3В.

Серед еталонів виділяють робочі, які служать для перевірки інших 3В і офіційно затверджені як зразкові. Наприклад, зразкова міра, зразковий вимірювальний перетворювач, зразковий прилад. До зразкових ЗВ належать також зразкові речовини і стандартні зразки.

Зразкова речовина - зразкова міра у вигляді речовини з відомими властивостями, яві відтворюються при додержанні умов приготування, що вказані в затвердженій специфікації.

Наприклад, чиста вода, чисті гази (водень, кисень), чисті метали (цинк, срібло, золото та ін.), неметали, сплави.

Стандартний зразок - міра для відтворення одиниць величин, що характеризують властивості або склад речовин і матеріалів (наприклад, стандартний зразок властивостей феромагнітних матеріалів, легованої сталі з атестованим вмістом хімічних елементів).

Робочі еталони атестують і перевіряють з допомогою інших, більш точних 3В. Таким способом здійснюється передавання розмірів одиниць ФВ від еталона до робочих 3В. Робочі 3В не можна застосовувати для перевірки інших 3В, якщо вони навіть точніші за наявні робочі еталони, оскільки вони не затверджені офіційно. Разом з тим робочі еталони не дозволяється використовувати як робочі ЗВ для виконання практичних вимірювань.

 

ЛІТЕРАТУРА

1. ДСТУ 2681-94. Метрологія. Терміни та визначення.

2. Обозовський С.С. Теоретичні основи інформаційно-вимірювальної техніки. Загальні питання і теорія похибок. -К.: НМК ВО, 1991. - 223 с.

3. Шишкін И.Ф. Теоретична метрологія. Підручник для вузів. -М.: "Издательство стандартов", 1991.- 492 с. (рос.).

4. Орнатский П.П. Теоретичні основи інформаційно-вимірювальної техніки. -К.: Вища школа, 1983. - 455 с. (рос.).

5. Новіцкий П.Г., Зоград І.А. Оцінка похибок результатів вимірювань. -Л.: "Єнергоатомиздат", 1985. - 248 с. (рос.).

6. Тюрін І.І. Вступ в метрологію. -М.: "Издательство стандартов", 1985. - 248 с. (рос).