Лекція, Основні поняття - статика

Лекція №3

Основні поняття

Дисципліна: Технічна механіка

План лекції:

1 Система сил, рівнодіюча і урівноважуюча сили

2 Аксіоми статики

1 Система сил, рівнодіюча і урівноважуюча сили

У більшості випадків тіла знаходяться під одночасним впливом декількох сил. Наприклад, на вагонетку при її рівномірному русі по рейках діють (рис. 6) F - сила тяги електровоза; Т - сила опору руху; Р - власна вага; N - сили тиску рейок на колеса.

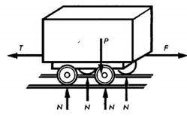
Рис. 6

Сукупність усіх діючих на тіло сил називають системою сил. Сили, що входять в систему сил, називають складовими силами.

У наведеному прикладі систему сил складають сім сил, дві з яких діють горизонтально, а решта вертикально.

Кожна система сил характеризується певним числом сил, їх величиною і напрямком. Залежно від напрямку складових сил розрізняють системи сил (рис. 6а): діючі по одній прямій, паралельно, що сходяться, довільно спрямовані. Складові сили можуть діяти в одній або декількох площинах.

а) діючі по одній прямій; б) паралельними; в) сили що сходяться; г) довільно спрямованими

Рис. 6(а) - Системи сил зі складовими силами

Відповідно до цього розрізняють плоску і просторову системи сил. Деякі системи сил можуть бути замінені однією силою, яка надає таку ж дію, що і замінні системи сил. Силу, яка виробляє рівноцінну дію системи сил, називають рівнодіюча силою.

Рівнодіюча сила визначається складанням складових сил. Якщо сили спрямовані по одній прямій, то рівнодіюча дорівнює сумі цих сил. Для випадку, зображеного на рис.6 (а), рівнодіюча сила

При цьому сили, що діють зліва направо, умовно прийнято за позитивні. В результаті складання сил рівнодіюча може вийде рівна нулю. В цьому випадку тіло знаходиться в рівновазі. Якщо ж рівнодіюча не дорівнює нулю, то для забезпечення рівноваги до тіла прикладається додаткова сила, яка призводить дану систему сил в стан рівноваги.

Висновок: урівноважувальна сила дорівнює за величиною рівнодіючій силі і протилежна їй за напрямком.

2 Аксіоми статики

Всі теореми і рівняння статики виводяться з декількох вихідних положень, прийнятих без математичних доказів і званих аксіомами або принципами статики. Аксіоми статики представляють собою результат узагальнень численних дослідів і спостережень над рівновагою і рухом тіл, неодноразово підтверджених практикою. Частина з цих аксіом є наслідками основних законів механіки, з якими ми познайомимося в динаміці.

Аксіома 1. Якщо на вільне абсолютно тверде тіло діють дві сили, то тіло може перебувати в рівновазі тоді і тільки тоді, коли ці сили рівні за модулем (F₁ = F₂) і спрямовані вздовж однієї прямої в протилежні сторони (рис. 6).

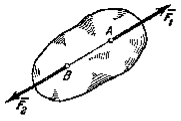
Рис.6. Система сил, що знаходиться в рівновазі

 Аксіома 1 визначає найпростішу врівноважену систему сил, так як досвід показує, що вільне тіло, на яке діє тільки одна сила, перебувати в рівновазі не може.

Аксіома 2. Дія даної системи, сил на абсолютно тверде тіло не зміниться, якщо до неї додати або від неї відняти врівноважену систему сил.

Ця аксіома встановлює, що дві системи сил, що відрізняються на врівноважену систему, еквівалентні один одному.

Слідство з 1-й і 2-й аксіом. Дія сили на абсолютно тверде тіло не зміниться, якщо перенести точку прикладання сили вздовж її лінії дії в будь-яку іншу точку тіла.

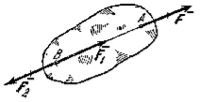
Рис.7. Система сил

Справді, нехай на тверде тіло діє прикладена в точці А сила (рис.7). Візьмемо на лінії дії цієї сили довільну точку В і докладемо до неї дві врівноважені сили і, такі, що, , . Від цього дію сили на тіло не зміниться. Але сили і за аксіомою 1 також утворюють врівноважену систему, яка може бути відкинута. В результаті на тіло. Діятиме тільки одна сила, рівна, але прикладена в точці В.

Таким чином, вектор, що зображає силу, можна вважати прикладеним в будь-якій точці на лінії дії сили (такий вектор називається ковзаючим).

Аксіома 3 (аксіома паралелограма сил). Дві сили, прикладені до тіла в одній точці, мають рівнодіючу, прикладену в тій же точці і зображує діагоналлю паралелограма, побудованого на цих силах, як на сторонах.

Вектор, що дорівнює діагоналі паралелограма, побудованого на векторах і (рис.8), називається геометричній сумою векторів і :.

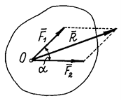
Рис.8. Рівнодіюча двох сил

 Величина рівнодіюча .

Отже, аксіому 3 можна ще формулювати так: дві сили, прикладені до тіла в одній точці, мають рівнодіючу, рівну геометричній (векторній) сумі цих сил і прикладену в тій же точці.

Аксіома 4 (принцип протидії). При будь-якому дії одного матеріального тіла на інше має місце таке ж по величині, але протилежне за направленням протидію.

Закон про рівність дії і протидії є одним з основних законів механіки. З нього випливає, що якщо тіло А діє на тіло В з силою  , то одночасно тіло В діє на тіло А з такою ж за модулем і спрямованого уздовж тієї ж прямої, але протилежну сторону силою (рис. 9). Однак сили і не утворюють врівноваженою системи сил, так як вони прикладені до різних тіл. Ця аксіома відповідає третьому закону Ньютона: дія завжди одно і протилежно протидії. При цьому необхідно пам'ятати, що в аксіомі 4 розглядається випадок, коли сили прикладені до різних тіл і в цьому випадку система сил не є врівноваженою на відміну від випадку дії сил в аксіомі 2.

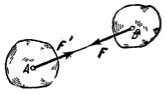
Рис.9. Протидія

Цей принцип стверджує, що в природі не існує односторонніх явищ. На рис. 10 зображена балка, яка спирається на стіни кінцями А і В. Для виявлення сил дії і протидії відділимо балку від стін. Тоді сили дії балки на стіну виражаються силами D_A і D_B, прикладеними до стін, а сили протидії - силами R_A і R_B, прикладеними до балки, які в подальшому будемо називати реакціями.

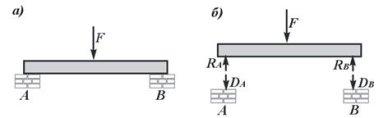
а - схема завантаження балки; б - сили дії балки на опори і протидії з боку опор на балку

Рис. 10. Обпирання балки на опори

Аксіома 5 (принцип затвердіння). Рівновага змінюваного (деформується) тіла, що знаходиться під дією даної системи сил, що не порушиться, якщо тіло вважати отверділим (абсолютно твердим). З принципу затвердіння слід, що умови, необхідні і достатні для рівноваги абсолютно твердого тіла, необхідні, але не достатні для рівноваги тіла, що деформується, за формою і розмірами тотожного з даними.

Висловлене в цій аксіомі твердження очевидно. Наприклад, ясно, що рівновага кола не порушиться, якщо її ланки вважати звареними між собою і т. д.

Аксіома 6 (аксіома зв'язків). Будь-яке невільний тіло можна розглядати як вільне, якщо механічна дія зв'язків замінити реакціями цих зв'язків (пояснення до цієї аксіоми в наступному параграфі).

Наведені принципи і аксіоми покладені в основу методів вирішення задач статики. Всі вони широко використовуються в інженерних розрахунках.

Контрольні питання

- Що називається системою сил?

- Наведіть приклади зосереджених і розподілених сил.

- Що називається рівнодіючої системи сил?

- Яка сила називається врівноважувальною?

- Дайте визначення зовнішньої і внутрішньої сили.

- Сформулюйте аксіому про рівновагу двох сил.

- Сформулюйте першу, другу, третю і четверту аксіоми статики.

Література

1 Кострыкин М.И., «Основы технической механики», Учебное пособие, Изд.2-е, переработ. М., «Машиностроение», 1973, 224с.

2 Кузе И., «Теоретична механіка», видавництво «Фоліо», 2017, 780с.

3 Мовнин М.С., Израелит А.Б., Рубашкин А.Г., «Основы технической механики», Л., «Машиностроение», 1979, 286с.

 4 Черныш О., Яременко В., Березовый М., «Теоретична механіка», Навчальний посібник -Центр навчальної літератури, 2018, 760с.