Лекція на тему "Піраміда, види пірамід"

Лекція:Піраміда, види пірамід

План

1.     Піраміда, види пірамід. Площі поверхонь.

2.     Застосування пірамід в навколишньому світі. 

Література

1.     Геометрія: 11 кл.: підруч. для загальноосвіт. навч. закл.: академ. рівень, проф. рівень / Г.П. Бевз, В.Г. Бевз, Н.Г. Владімірова, В.М. Владіміров. – К.: Генеза, 2011. – с. 152-164.

2.     Математика. Комплексна підготовка до ЗНО і ДПА / Уклад.

А.М. Капіносов [та ін.]. – Тернопіль: Підручники і посібники 2017. – с. 429.

1. Піраміда, види пірамід. Площі поверхонь

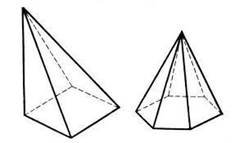Пірамідою називається многогранник, одна грань якого – довільний многокутник (nкутник), а інші грані – трикутники (бічні грані), що мають спільну вершину.

Спільну вершину бічних граней називають вершиною піраміди, а n-кутник (може бути трикутник, чотирикутник, п’ятикутник і т.д.) – основою піраміди.

Відрізки, що сполучають вершину піраміди з вершинами основи, називаються бічними ребрами.

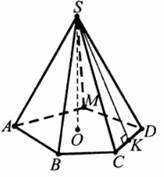Висота піраміди — перпендикуляр, опущений із вершини піраміди на площину основи.

На рисунку ABCDM – основа піраміди, S – вершина, SA, SB, SC, SD, SM – бічні ребра, SO – висота (SO (ABC)).

Властивості:

-    Якщо всі бічні ребра нахилені до площини основи під однаковим кутом, то вони рівні й вершина піраміди проектується в центр кола, описаного навколо основи піраміди.

-    Якщо всі бічні грані піраміди нахилені до площини основи під однаковим кутом , то вершина піраміди проектується в центр кола, вписаного в основу піраміди, а площа основи піраміди дорівнює добутку площі бічної поверхні та косинуса кута :

Sосн  Sб cos.

Піраміду називають правильною, якщо її основою є правильний многокутник, а основа висоти збігається з центром цього многокутника. У правильній піраміді висота SK бічної грані, проведена з її вершини, - апофема.

Алгоритм побудови правильної трикутної піраміди

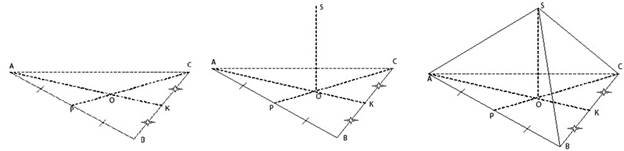
            Площа    бічної    поверхні    правильної    піраміди    обчислюється     за

_б 1 _осн    - апофема. формулою: S         P          l , де l

2

Площа повної поверхні обчислюється за формулою: S_п  S_б  S_осн.

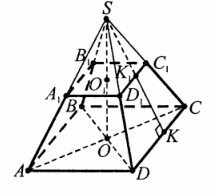Зрізана піраміда – многогранник, який відтинається внаслідок перетину піраміди площиною, паралельною її основі.

ABCD – нижня основа, A₁B₁C₁D₁ – верхня основа.          Висота        ОО₁   – відрізок       прямої, перпендикулярної до основ й обмежений ними.

Правильна зрізана піраміда — це зрізана піраміда, яку дістали з правильної піраміди.

Основи – правильні многокутники. Відрізок, який з’єднує центр основ, є вистою.

Площа бічної поверхні обчислюється за формулою: S_б  ^{Р1  Р2} m, де P₁ 2

і P₂ - периметри основ, m- апофема, m= К₁К.

Площа повної поверхні обчислюється за формулою: S_п  S_б  S₁  S₂, де

S₁ і S₂ - площі основ.

2. Застосування пірамід в навколишньому світі В житті ми часто зустрічаємось з пірамідами.

Ще 2-3 тис. років до н.е. форми пірамід використовували у побудовах гробниць для фараонів (Хеопса, Хефрена, Мікерина). З давнини піраміди входять в число семи Чудес світу.

Найбільша гробниця – Хеопса - була побудована в 27 столітті до н.е. архітектором  Хеміуном і спочатку досягала висоти 147 м.

Піраміда Місяця знаходиться в Мексиці. Час спорудження – кінець 1 тис. до н.е. -  початок н.е. Висота 42 м.

Піраміда Сонця – п'ятиярусна піраміда, знаходиться в Мексиці. Час спорудження – кінець 1 тис. до н.е. - початок н.е. Висота 64,5 м.

В 1776 р. Конгресом США прийнято ескіз державної   печатки       зі       зрізаною пірамідою. Якщо          подивитися          на американську купюру в $1, то на її звороті й нині можна побачити зрізану піраміду, а над нею - трикутник із оком посередині.

Дизайнери-архітектори використовують пірамідальні форми при побудові будинків, ліхтарів на вулиці, дахів на каплицях, церков.

Пірамідальні форми також використовують при виготовленні упаковки     для    продуктів    в

промисловості (наприклад, пакетики чаю у вигляді пірамід; упаковка томатної пасти і т.д.).

Домашнє завдання

1.     Вивчити теоретичний матеріал.

2.     Навести із повсякденного життя приклади предметів, які мають форму піраміди.