Логарифмічна функція. Розв’язання логарифмічних рівнянь.

Тема уроку: Логарифмічна функція. Розв’язання логарифмічних рівнянь.

Цілі уроку:

Розвивальна (дидактична): сприяти розвитку:

- вмінь правильно добирати та застосовувати способи розв’язування логарифмічних рівнянь, адекватні до певних типів, розпізнавати логічно некоректні міркування, критично й творчо мислити (загальні навчальні компетенції);

- здатності лаконічно, чітко та аргументовано формулювати і висловлювати свої судження, самостійно працювати з підручником, опрацьовувати математичні тексти, шукати й використовувати додаткову навчальну інформацію, оцінювати здобуту інформацію;

- навичок самоконтролю та вмінь виступати з повідомленнями.

Навчальна (методична): формувати математичні компетенції: знання поняття логарифмічного рівняння, найпростішого логарифмічного рівняння; здатності до застосування загальних способів розв’язування рівнянь (застосування рівнянь-наслідків та рівносильних перетворень рівнянь), спеціальних методів розв’язування логарифмічних рівнянь (через означення та властивості логарифмів, потенціювання, способів заміни змінних, зведення логарифмів до однієї і тієї самої основи); вміння розв’язувати  логарифмічні рівняння різних типів (предметні компетенції).

Виховна: сприяти вихованню цілеспрямованості, наполегливості у досягненні поставленої мети, прищеплювати бажання мати якісні, глибокі знання, виховувати культуру математичної мови та мислення, сталий інтерес до вивчення математики; зміцнювати почуття гордості за свій народ на прикладі життєвого та творчого шляху видатних українських математиків (особистісні компетенції).

Тип уроку: вивчення знань та формування вмінь.

Елементи педагогічних технологій: індивідуальної, колективної, роботи, роботи в парах; технології «Мікрофон» (теоретична розминка), тестового контролю – «Тест» (практична розминка), формування навичок проектної діяльності, інтерактивної технології  («Рівний рівному»), ігрової (гра «Знайди помилку»); прийомів «Якщо залишається час», використання виховної «Ліричної хвилинки».

Випереджувальне завдання: кожна з чотирьох груп готує доповіді-проекти.

Міждисциплінарні зв’язки: алгебра, фізика, інформатика;

Технічні засоби навчання: комп’ютер, мультимедійний проектор.

Методичне забезпечення: випереджальні завдання, презентація, картки-завдання для математичного лото, портрети видатних математиків, пам`ятка «Властивості логарифмів», опорний конспект «Логарифмічні рівняння».

Структура та зміст уроку

1.Організаційна частина.

Привітання учнів. Перевірка готовності до заняття учнів, класу, обладнання.

1.1. Етап орієнтації

Позитивна установка на роботу. Вступне слово вчителя (слайд 1)

Вчитель: Я сподіваюся, що наше заняття пройде цікаво, з великою користю для всіх. Дуже хочу, щоб ви відчували себе впевнено, щоб ви були задоволені собою. А людина тоді задоволена – коли досягає певних успіхів, долає якісь перешкоди, коли каже: “Мені це вдалось”. Будьте дуже уважні протягом заняття. Думайте, питайте, пропонуйте – бо шляхом до істини нам з вами йти разом.

2. Мотивація навчання

Вчитель звертається до учнів із словами С.Ковалевської «… Мені здається, що поет повинен бачити те, чого не бачать інші, бачити глибше, ніж інші. Це саме повинен і математик». (слайд 2)

Рівняння – одна з провідних тем курсу математики, оскільки розв`язування багатьох практичних задач зводяться до складання й розв`язування рівнянь. Причому багато задач, різноманітних за змістом та з різних галузей діяльності людини, зводяться до рівняння певного виду, яке служить знаковою моделлю цієї групи задач. Уміння розв’язувати певний вид рівнянь дає можливість розв`язувати цілу групу задач. Метод рівнянь - один з математичних методів пізнання реальної дійсності. Алгебру називають теорією розв’язування рівнянь. Різноманітність видів рівнянь відображає наступна схема «Сходинки знань» (схема 2.1.)

 

Схема 2.1.

						7
					6
				5
			4
		3
	2
1
АЛГЕБРАЇЧНІ				ТРАНСЦЕНДЕНТНІ
РІВНЯННЯ

 

Опора на особистий досвід учнів

Відкрити перші шість сходинок, узагальнити знання про рівняння, які отримали протягом шкільного курсу, учням пропонується через знаходження відповідності між рівняннями та їх видами (Таблиця 2.1).

1) Співвіднесіть рівняння з його видом. Відповідь обґрунтуйте.

Таблиця 2.1.

№ сходинки	Рівняння	Вид	Код
1		показникові	Д
2		лінійні	Д
3		Ірраціональні	В
4		Дробово-раціональні	С
5		Квадратні	О
6		тригонометричні	І

Схема 2.2.

						Логарифмічні
					Показникові Д
				Тригонометричні І
			Ірраціональні В
		Дробово-раціональні С
	Квадратні О
ЛінійніД
АЛГЕБРАЇЧНІ				ТРАНСЦЕНДЕНТНІ
РІВНЯННЯ

 

Після правильного виконання завдання студенти отримають слово “Досвід”. Піднімаючись по “Сходинкам знань” протягом навчального курсу математики ви нарешті досягли останньої сходинки.

3. Повідомлення теми, формування мети та основних завдань уроку.

Для визначення теми уроку, над якою вони будуть працювати, а також мети і місця даного заняття в системі занять теми «Логарифмічна функція», учням пропонується визначити вид наступних рівнянь і відкрити останню сьому сходинку.

2) Визначити вид наступних рівнянь

                            

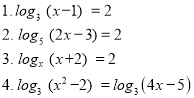
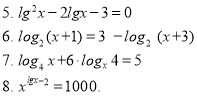
Учні формулюють означення логарифмічного рівняння, і відкривається остання сьома сходинка в схемі 2.2.

Означення: Логарифмічними рівняннями називають рівняння, які містять змінну під знаком логарифма.

Повідомлення теми і мети заняття. Учитель разом з учнями визначає особистісно значущі завдання тієї діяльності, яку передбачено здійснити протягом заняття.

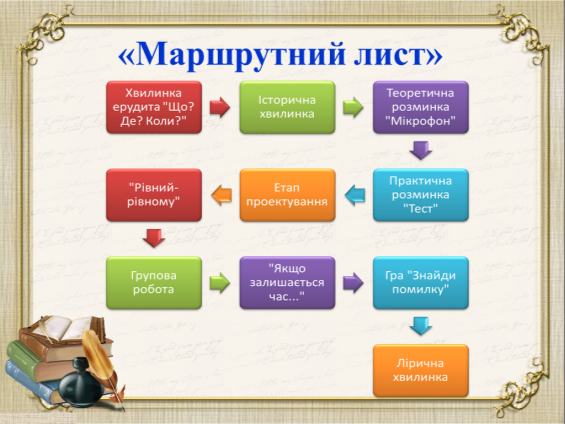
Вчитель: Сьогодні ми будемо набувати вміння розв’язувати логарифмічні рівняння. Результатом роботи стане опорний конспект (додаток  Б), який буде вам допомагати на заняттях та іспитах в подальшому житті. Визначити рівень своїх досягнень з даної теми ви зможете на наступному занятті під час виконання самостійної роботи. Логарифмічні рівняння треба навчитися розв’язувати. Досягати мету заняття ми будемо за поданим маршрутним листом.(Рис 2.1)

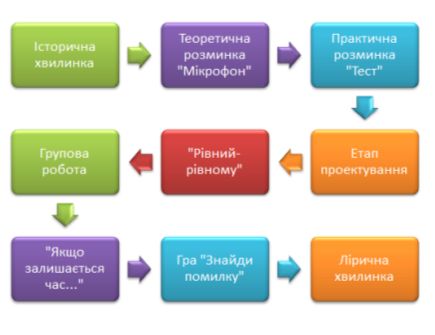
Рис 2.1 Маршрутний лист уроку

4. Актуалізація опорних знань

 «Багато чого з математики не залишається в пам’яті, але коли розумієш її, тоді легко при нагоді згадати призабуте».

М. В. Остроградський

4.1. Історична хвилинка

Випереджальне завдання – повідомлення про видатного російського математика почасти українського походження, письменницю і публіциста С.Ковалевську.

Заочне знайомство С.Ковалевської з українським математиком М. В. Остроградським.

Коли Соні виповнилося 11 років, під час зимового перебування родини Крюковських у Петербурзі викладачем математики до неї запросили лейтенанта флоту О. М. Страннолюбського. Вже на перших заняттях викладача здивувало те, що дівчина так швидко засвоювала перші поняття з вищої математики — поняття границі, похідної тощо, “начебто вона їх раніше знала”. Соня пояснила: «У ту хвилину, коли ви пояснювали мені ці поняття, мені раптом пригадалося, що все це було написано в лекціях Остроградського, якими була обклеєна наша кімната, і саме поняття про границю здалося мені давно відомим».

Для розв’язування логарифмічних рівнянь потрібно знати основні відомості про логарифм та його властивості, властивості логарифмічної функції. Оцінити рівень засвоєння і розуміння навчального матеріалу з попередніх тем «Логарифм. Властивості логарифма. Логарифмічна функція», здійснити корекцію адекватності оволодіння навчальною інформацією, учням пропонується за допомогою розминки, теоретичної і практичної.

4.2. Перевірка теоретичних знань учнів

 «Найкраща помилка та, яку допускають під час навчання»”.

Г.С.Сковорода

Теоретична розминка. Технологія «Мікрофон».

1. Що називають логарифмом числа b за основою a ?

2. Який логарифм називають десятковим і який натуральним?

3. Сформулюйте формули логарифмування.

4. Сформулюйте формулу переходу до логарифмів з іншою основою.

5. Яка функція називається логарифмічною?

6. Яка множина чисел є областю визначення логарифмічної функції?

7. При якому значенні а функція зростає на всій області визначення?

8. При якому значенні а функція спадає на всій області визначення?

4.3. Практична розминка

Тест

Для успішного розв’язування вправ на заняті учням пропонується відповісти на питання тесту і пригадати вивчене на попередніх заняттях.

До речі слово «test» в перекладі з англійської мови означає «випробування». Вперше його застосував у серпні 1966 року професор В.Серве з Бельгії. Отже, тестовій перевірці майже 50 років.

Тест

1.Який з виразів має зміст?

 

А	Б	В	Г	Д

 

2. Яка з рівностей правильна?

 

А	Б	В	Г	Д

 

3. Областю визначення функції    є проміжок:

 

А	Б	В	Г	Д

 

 

4. Знайти значення х, якщо   

 

А	Б	В	Г	Д
18	11	9	24	27

 

5. Установіть відповідність між виразами (1-4) і їх числовими значеннями (Б-Д). (слайд 10)

1.	Д. 2
2.	Б. 0
3.	В.
4.	Г. 1

 

Самоперевірка  знань студентів. Перевір себе! (слайд 11)

 

Бланк правильних відповідей

 

1	2	3	4			Б	В	Г	Д
В	Б	Д	Г		1
					2
					3
					4

 

Відбувається корекція знань.

4.4. Етап проектування.

Залучення учнів до проектування діяльності, яка здійснюватиметься на занятті, через попередню роботу (поділ групи на чотири групи, випереджувальні завдання, повідомлення, презентації), складання та обговорення плану наступної роботи, яку передбачено виконати.

І група

Історична довідка: винахід логарифма, десяткові логарифми.(слайд 12-13)

Алгоритм розв’язання логарифмічного рівняння методом застосування властивостей логарифма:

ІІ група

Історична довідка: логарифмічна спіраль, техніка і логарифми.(слайд 14-15)

Алгоритм розв’язання логарифмічного рівняння методом введення нової змінної:

ІІІ група

Історична довідка: музика і логарифми.(слайд 16)

Алгоритм розв’язання логарифмічного рівняння методом логарифмування обох частин рівняння:

ІV група

Історична довідка: логарифми навколо нас.(слайд 17)

Алгоритм розв’язання логарифмічного рівняння методом зведення до однієї основи:

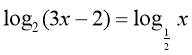
5. Узагальнення та систематизація знань.

Прийом «Рівний – рівному»

Розв`язання найпростіших логарифмічних рівнянь.

Вчитель пропонує учням із розглянутих вище логарифмічних рівнянь вибрати ті рівняння, які вони можуть розв’язати спираючись на власний досвід.

Вводиться означення найпростіших рівнянь.

Розв'язання найпростіших логарифмічних рівнянь демонструють 5 учнів-консультантів, які самостійно випереджально опрацювали матеріал, і отримали консультацію вчителя. (слайд 18, таблиця 2.2.)

 

Таблиця 2.2.

Найпростіше логарифмічне рівняння
Метод використання означення логарифма- за допомогою рівносильних перетворень	Метод потенціювання
В загальному випадку   1 учень Розв`язати рівняння 1 2 учень Розв`язати рівняння 2 3 учень Розв`язати рівняння 3	В загальному випадку   4 учень Розв`язати рівняння 4 І спосіб   5 учень Розв`язати рівняння 4 ІІ спосіб

 

5.2.Групова робота 

Групи сформовані за рівнем математичної підготовки учнів на початку уроку. Кожна група повинна розглянути розв`язання даного логарифмічного рівняння, користуючись довідковою таблицею 2.3, яка містить основні поняття, властивості, орієнтири для пошуку плану розв’язування. Діти, консультуючись один з одним, виконують завдання. В кожній групі є підготовлений консультант, який контролює виконання завдань, своєчасно надає допомогу. Після виконання цього завдання, представник від кожної групи демонструє розв`язання свого рівняння на дошці з поетапним коментуванням. До розв`язування рівняння аналогічного типу запрошуються за бажанням учні з інших груп. За результатом спільної роботи всіх груп складається опорний конспект з пошуку розв`язання логарифмічних рівнянь.

Таблиця 2.3.

Пам`ятка!	Властивості логарифмів
- основна логарифмічна тотожність - логарифм добутку - логарифм частки - логарифм степеня - формула переходу до нової основи

 

І група - Метод зведення логарифмічного рівняння до алгебраїчного методом заміни

Розв`язати рівняння

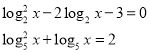
ІІ група - Метод застосування властивостей логарифма, для рівнянь, які містить алгебраїчну суму логарифмів з однаковою основою

Розв`язати рівняння

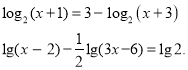
ІІІ група - Метод зведення логарифмів до однієї і тієї ж основи

Розв`язати рівняння

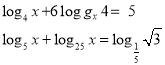
ІV група - Метод логарифмування обох частин рівняння

Розв`язати рівняння

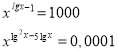
6. Підведення підсумків, оцінювання знань студентів.

Під час розв’язування логарифмічних рівнянь допускаються ряд помилок на які потрібно звертати увагу.(слайд 20)

6.1 Гра “Знайди помилку”

1. =1 ОДЗ: Відповідь:	2. x=0; Відповідь:
3. =25; Відповідь:	4. 2 = -2; Відповідь:

6.2. Лірична хвилинка

Вправа на розвиток уваги

Вчитель пропонує учням прослухати вірш Г. П. Бевза про М. Остроградського і визначити членом академії наук в яких країнах він був обраний:

Талантами багата Україна!

Хай навіть відбиваючись від орд.

Долаючи неволю і руїни,

Все ж геніїв народжує народ.

Один із них- Михайло Остроградський-

Великий тілом, розумом і духом,

Найперший вчений у Краю Козацькім,

Властитель теорем і аксіом.

Ньо-Йоркський академік і туринський,

Паризький, римський-між усіх широт

Відомий математик український,

Славетний український патріот.

Г.П. Бевз

(М. В. Остроградський  був вперше з українських математиків обраний членом академії наук у Нью-Йорку, Туринської академії, Національної академії Деї Лінчеї в Римі, членом-кореспондентом Паризької академії наук).

Історична хвилинка Випереджальне завдання - Повідомлення  про українського математика М.Остроградського (слайд 21).

Рефлексія навчальної діяльності

Вчитель: Дуже часто показником успіху в житті є не тільки кінцевий результат, а й процес його досягнення. Вміння аналізувати є дуже важливим у наш насичений інформацією час. Людиною, що вміє аналізувати, практично неможливо маніпулювати, вона завжди знайде вихід з будь-якої ситуації. Саме час повернутися до початку заняття, до мети, яку ми перед собою поставили.

Поміркуйте:

• Чи досягли ми її, чи розширили ми знання про рівняння?
• Чи змогли удосконалити свою компетентність з даного питання?
• Чи вичерпав ти свої можливості?

Крім того, треба дати відповідь на запитання:

• Що допомогло вам досягти успіху?
• Чи справдилися ваші очікування від заняття?
• Чи отримав ти задоволення від власної праці?

У вас є 1-2 хвилини для обговорення результатів сьогоднішньої роботи. Учні висловлюють свою думку, підводять загальний підсумок:

Інтерактивна вправа “Незакінчене речення”

1. Сьогодні на занятті було головним…..

2. Сьогодні на занятті я узагальнив теоретичні факти …

3. Сьогодні на занятті я розширив свої знання про…

4.Сьогодні на занятті я набув практичних вмінь…

5.Необхідно додатково попрацювати над….

6. Найважчим для мене було ….

7. Протягом заняття я переживав емоційний стан…

8. Цікавим на занятті було…

9. Досягти успіху мені допомогло ….

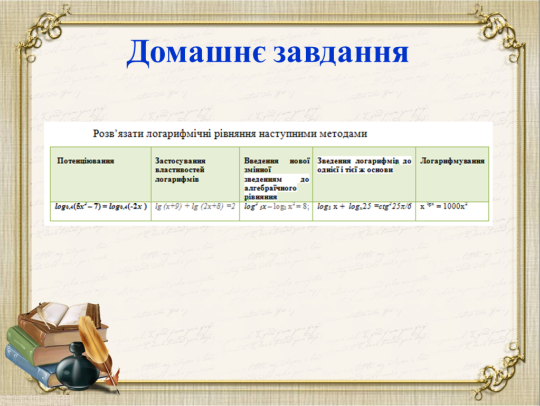
7. Маршрут (Домашнє завдання).

Опорний конспект (Логарифмічні рівняння)

 

 

 

 

 

 

 

 

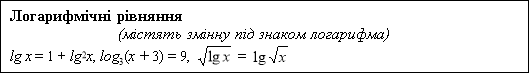
Застосування         Застосування

означення                 Потенціювання                властивостей           Заміна змінної          Логарифмування

логарифма логарифма

     

 

 

 

 

 

А. Рівняння виду   logа f(х )= с метод роз`в’язання – застосування означенням логарифма (ОДЗ можна не записувати, оскільки  вона враховується автоматично) Алгоритм f(х )= ас. Записати відповідь.	С- містить алгебраїчну суму логарифмів з однаковою основою метод роз`в’язання – застосування властивостей логарифма Алгоритм 1. Знайти ОДЗ. 2. Застосувати властивості (4-6)      справа-наліво. 3. Отримаємо рівняння виду А чи В. 4. Розв`язати рівняння. 5. Виконати перевірку коренів, шо ввійшли в ОДЗ, 6. Записати відповідь.
	D – рівняння виду  k logа 2 f(х)  f(х )+ m logа f(х) +p = 0 метод роз`в’язання –заміна змінної Алгоритм 1. Знайти ОДЗ. 2.Виконати заміну logа f(х)= у. 3.Розв`язати квадратне рівняння відносно у. 4. Повернутися до заміни і знайдемо х. 5.Виконати перевірку коренів, що ввійшли в ОДЗ. 6.Записати відповідь.
В. Рівняння виду  logа f(х )= logа g(х ) (а>0, а ≠ 1) метод роз`в’язання – потенціювання   (за допомогою рівносильних перетворень)   Алгоритм Знайти ОДЗ f(х) >0 g(х)>0   2. Розв`яжемо рівняння  f(х )=  g(х ) 3. Виконаємо перевірку коренів, що ввійшли до ОДЗ. 4. Записати  відповідь.	F   - містить логарифми з різними основами метод роз`в’язання – зведення логарифмів до однієї основи Алгоритм 1. Знайти ОДЗ. 2. Застосувати властивості (7-8, 2-3). 3. Після перетворень рівняння набуде вид С або  D. 4.  Розв`язати рівняння виду С або  D. 5. Виконати перевірку коренів, шо ввійшли в ОДЗ, 6.Записати відповідь.
	Р – рівняння виду = Q(x). метод роз`в’язання – логарифмування Алгоритм 1. Знайти ОДЗ. 2. Прологарифмувати обидві частини рівняння. 3. Після перетворень рівняння набуде D. 4.Виконати перевірку коренів, що ввійшли в ОДЗ.5 5.Записати відповідь.

Презентація до уроку-практикуму з теми «Логарифмічна функція. Розв’язання логарифмічних рівнянь»