Урок узагальнення "Функції"

Тема уроку:Функції, їх властивості. Побудова графіків функцій за допомогою геометричних перетворень.

Мета уроку:  Узагальнити та систематизувати знання учнів про властивості та графіки основних видів функцій, елементарні перетворення графіків функцій ; відтворити вміння виконувати елементарні перетворення графіків функцій; розвивати інтелект учнів, уміння аналізувати, класифікувати, порівнювати, робити умовиводи за аналогією; виховувати позитивне ставлення учнів до навчально-пізнавальної діяльності.

Обладнання: комп’ютер зі встановленою програмою GRAN 2D.

ХІД УРОКУ

1. Організаційний момент.
2. Актуалізація опорних знань. На минулому уроці ви повторили властивості функцій. Тож дайте відповідь на такі питання:

1) Дайте означення області визначення функції. (Учні дають означення, а вчитель узагальнює : тобто, знайти область визначення функції означає з’ясувати, яких значень може набувати x) ;

2)Якщо , то …()

 3) Як знайти область визначення функцій   (), (), y=tgx , y=ctgx ?

4) Дайте означення області значень функції. (Тобто, знайти область значень функції означає з’ясувати, яких значень набуває y при усіх допустимих значеннях x);

5) Вкажіть множину значень функцій , , , , ,

6)Яка функція називається оборотною?оберненою?

7) Як побудувати обернену функцію?

8)Яка функція називається парною? Непарною?

9) Чи можна визначити парність та непарність функції , якщо функція задана явно(у=)? Якщо можна то як?

10) Як за допомогою графіка дослідити функцію на парність чи непарність?

11)Яку функцію називають періодичною ? Які періодичні функції ви знаєте?

12)Користуючись похідною ми можемо знайти …?(критичні точки; проміжки зростання, спадання; точки мінімуму та максимуму)

III. Перевірка домашнього завдання.

Учитель виводить на екран готове розв’язання , учні перевіряють та оцінюють свою роботу.

IV. Мотивація навчальної діяльності.

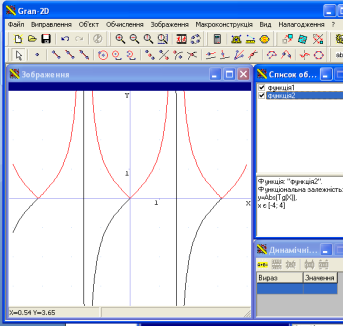
Сьогодні ми узагальнимо та систематизуємо усі отримані знання у школі про функцію, особливо перетворення графіків функцій. Для побудови графіків функцій використовуватимемо програму  GRAN 2D. Ця програма дасть можливість раціонально використати наш час, розв’язати велику кількість завдань, а виконуючи домашнє завдання, ви зможете перевірити правильність його виконання

V. Розв’язування задач і вправ.

1)Давайте згадаємо графіки основних функцій та основні перетворення графіків

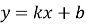• – лінійна функція. Побудуємо графіки ,

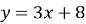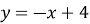
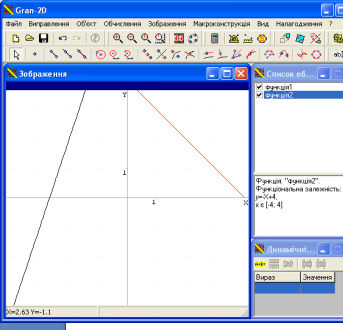
Учні роблять висновок про графік функції в залежності від а.

- парабола. Які перетворення потрібно здійснити, щоб отримати функції   ? Побудуємо графіки цих функцій в одній системі координат.(побудова здійснюється поступово при чому при побудові цих та наступних функцій, вчитель обов’язково вказує як в програмі GRAN 2D позначається множення, степінь, модуль,логарифм і т.д.)

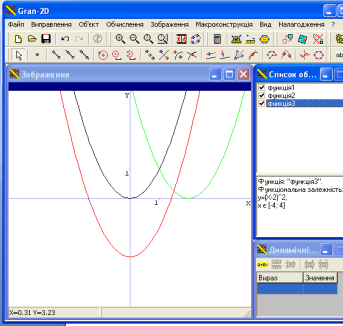
Отже, графік функції можна отримати в результаті паралельного перенесення  графіка функції на b одиниць угору, якщо b, і на -b вниз, якщо b, а

Графік функції можна отримати в результаті паралельного перенесення  графіка функції на b одиниць уліво, якщо b, і на -b управо, якщо b.

Серед побудованих функцій є парні? Назвіть будь ласка нулі функцій.

• Що ви можете сказати про функції 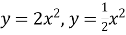? Побудуємо їх в дній системі координат.Учні роблять висновок про як отримати графік функції 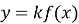, маючи .

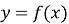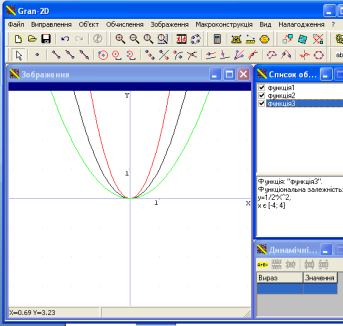
• Що ви можете сказати про перетворення виду , ?

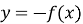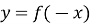Що перевірити, чи ви праві побудуємо графіки функцій

,.

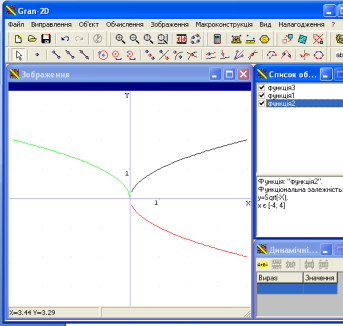
Скажіть яка область визначення кожної з функцій? Область значень?

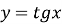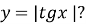
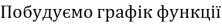
• Як з графіка функції  отримати 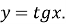Опишіть властивості цієї функції.

А тепер побудуємо . Отже ……

• 

 

Тобто, щоб побудувати графік функції усі точки графіка функції  з невід’ємною ординатою залишаються без змін , а точки розміщені нижче осі абсцис симетрично відображаємо відносно осі абсцис.

А як же побудувати графік функції ? Побудуємо спочатку графік функції , нагадайте властивості цієї функції? А тепер побудуємо  . Як змінився графік першої функції? (Учні узагальнюють план побудови).

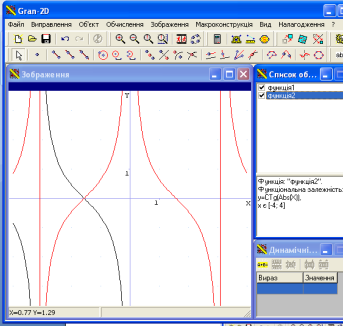
Чи можете назвати функцію таку,  щоб =.Вчитель наводить приклад:

Функція   гіпербола. А функції однакові.

 

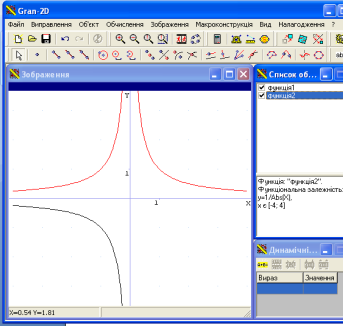
• А тепер перейдемо до обернених тригонометричних функцій

Давайте перевіримо вас, побудуємо графік цієї функції, а також побудуємо функцію .(Учитель з учнями обговорює властивості , щоб учні краще відтворили властивості функції доцільно побудувати графік функції )

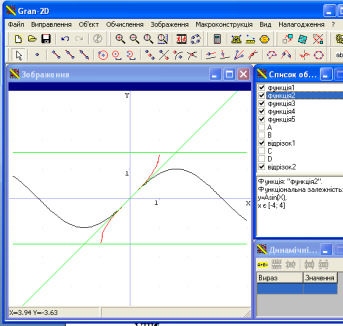
Аналогічно розглядають інші обернені тригонометричні функції.

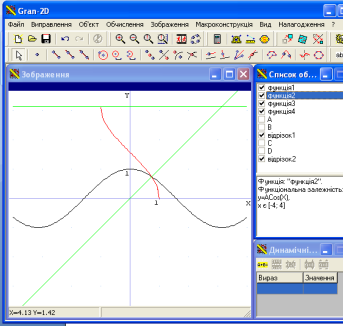
• Розглянемо ще й графіки таких функцій

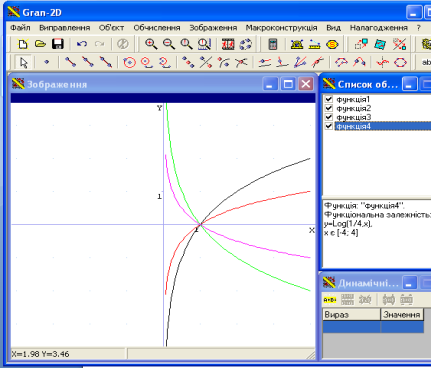
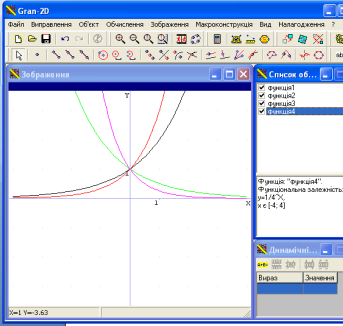
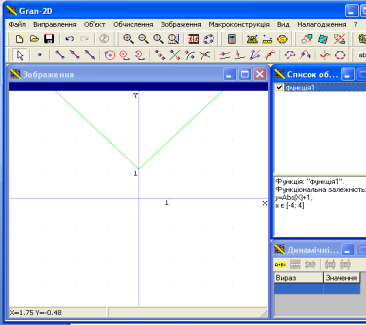
2).Побудуйте графік функції . у = │х│+ 1.

(До побудови кожного наступного графіка функцій, учні усно складають схему побудови , здійснюють покрокові побудови та звіряються з отриманим графіком в програмі; з побудованого графіка знаходять область визначення,значень;проміжки монотонності; точки перетину з осями системи координат; досліджують на парність;знаходять період, якщо функція періодична; екстремальні точки, мінімальне та максимальне значення функції)

(Графік функції , отримаємо відобразивши частину графіка , розміщену нижче від осі абсцис,симетрично до осі абсцис. А отримаємо з , якщо перенесемо його на одну одиницю вгору(доцільно будувати по етапах )

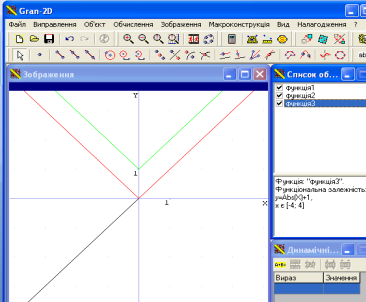
Б).

.

, ), точки перетину графіка з осями координат, але краще скористатись таким способом (тому, що а не завжди дорівнює одиниці)-1 (парабола перенесена на дві одиниці вправо та на одну одиницю вниз).

(ту частину графіка яка знаходиться справа від осі ординат симетрично відображаємо відносно цієї осі)

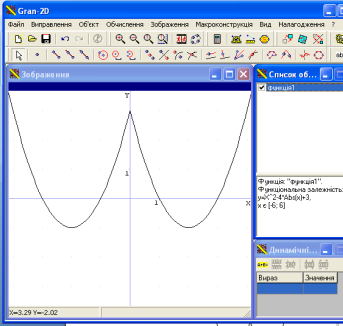
Що ви можете сказати про парність цієї функції? Проміжки монотонності?

В)

Побудова:

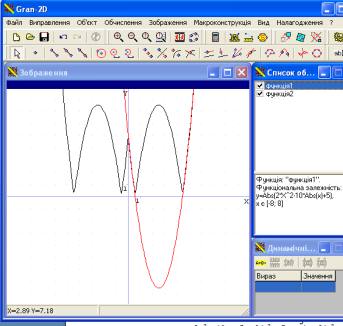
Щоб, переконатись, що   учитель будує вільну точку яка є вершиною параболи і звіряє її координати з отриманими ()

 

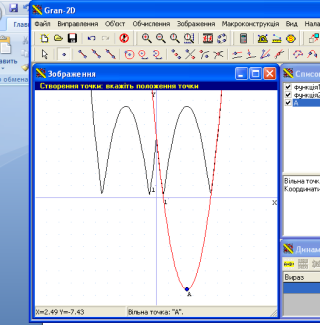
Г).

Побудова

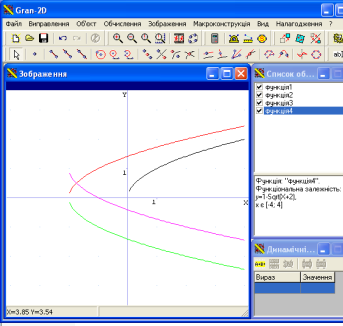
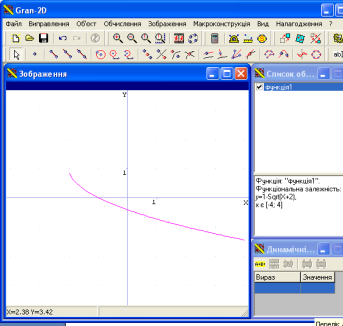
Д)

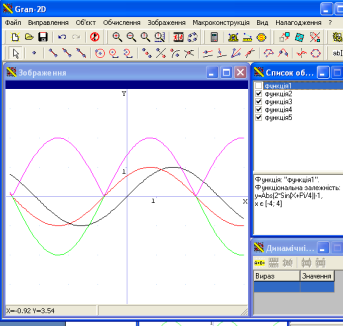
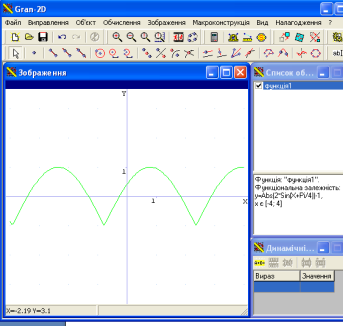
Е)

 

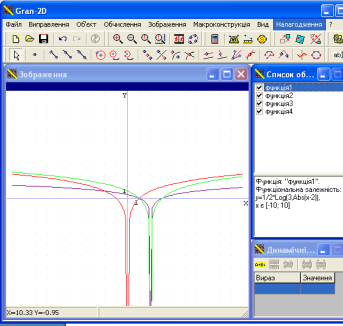
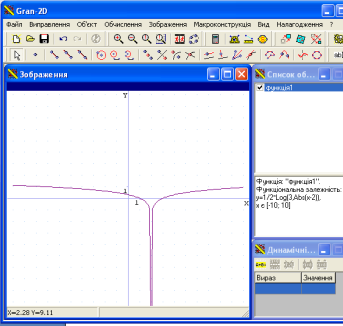
Є) . При побудові даної функції потрібно обов’язково врахувати область визначення функції.

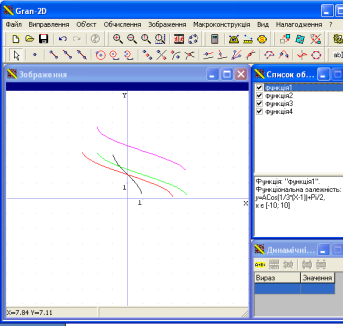
VI.Творча робота в групах. Учитель пропонує учням самостійно побудувати графіки функцій в одній системі координат різними кольорами

1),

;

1)

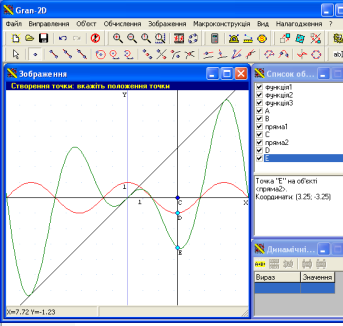
Чи не можна з графіків отримати графік функції

Якщо учні не можуть відповісти, учитель також будує ці графіки та показує як утворюється графік функції з графіків ( доцільно через довільну точку провести пряму перпендикулярну до вісі абсцис , який перетне графіки в деяких точках).

4)

VII.Підсумок уроку.

VIII.Домашнє завдання .

Побудувати в програмі GRAN 2D графіки функцій та описати їх властивості.

1)

2)

3)

4)

Знайти  функцій для яких виконується =

IX.Виставлення оцінок