Ляпунов Олександр Михайлович
Про матеріал
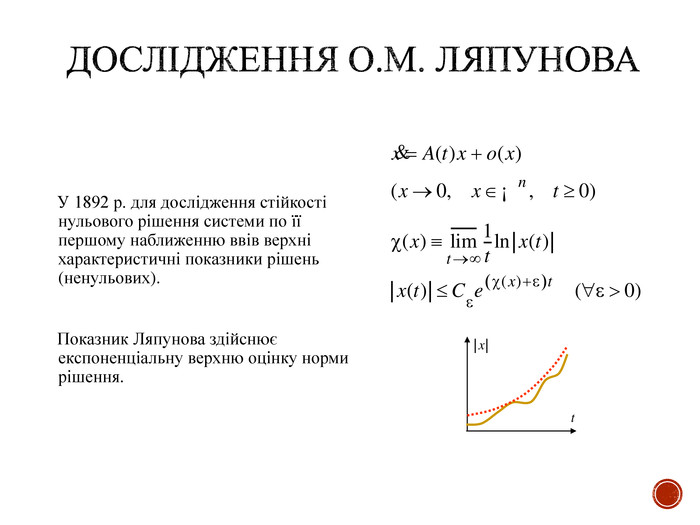
Презентація містить біографічну інформацію про родину, дитячі роки, освіту, доросле життя математика Олександра Михайловича Ляпунова, інформацію про його дослідження та досягнення. Автор презентації Когут Лариса Миколаївна. Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку