АБСОЛЮТНЕ ПІДСУМОВУВАННЯ РЯДІВ МАТРИЧНИМИ МЕТОДАМИ Дипломна робота на здобуття ступеня вищої освіти магістр
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ХЕРСОНСЬКИЙ ДЕРЖАВНИЙ УНІВЕРСИТЕТ
Факультет комп’ютерних наук, фізики та математики
Кафедра алгебри, геометрії та математичного аналізу
Абсолютне підсумовування рядів матричними методами
Дипломна робота
на здобуття ступеня вищої освіти магістр
Виконала: студентка 2 курсу 221M групи
Заочної форми навчання
Напряму підготовки 6.040201.Математика
Камінська Юлія Віталіївна
Керівник: к. фіз.-мат. наук, доцент
Кузьмич В. І.
Рецензент: д. пед. наук, проф. Шерман М.І.
Херсон – 2019
ЗМІСТ
ВСТУП……………………………………………………………………... 5
РОЗДІЛ 1. Підсумовування збіжних рядів…………………… 8
1.2. Лінійні перетворення рядів……………………………………...…11
1.3. Теорема Абеля і почленне диференціювання та інтегрування рядів………………………………………………………………………...12
1.4. Перетворення рядів за Ейлером …..……………………………….13
1.5. Перетворення рядів за Куммером…...……………………………..14
РОЗДІЛ 2. Підсумовування розбіжних рядів………………...23
2.1. Підсумовуючі функції….…………………………………………..23
2.2. Підсумовування за Пуассоном – Абелем………….……………...27
2.3. Лінійність і регулярність підсумовування за Пуассоном – Абелем
……………………………………………………………………………...29
2.4. Абсолютна збіжність методу Пуассона - Абеля ………………....32
2.5. Теорема Таубера .…………………………………………………..33
2.6 Підсумовування за Чезаро…………………………………………33
2.7 Співвідношення між підсумовуванням за Чезаро і за Пуассоном – Абелем……………………………………………………………………..33
2.8 Підсумовування за Ейлером………………………………………..33
2.9 Інші методи підсумовування розбіжних рядів……………………33
РОЗДІЛ 3. ПРЯМІ ТЕОРЕМИ ТЕОРІЇ АБСОЛЮТНОГО ПІДСУМОВУВАННЯ РЯДІВ ………………………………….………36
3.1 Загальні умови абсолютного включення та абсолютної рівносильності методів підсумовування (Барон)………………………40
3.2 Абсолютне включення та абсолютна рівносильність методу середніх арифметичних……………………………………………….....45
Висновки……………………………………………………………50
Список використаної літератури………………………………….60
Вступ
Ряди широко використовуються в математиці, особливо при дослідженні різноманітних технічних проблем, пов’язаних з наближеним інтегруванням диференціальних рівнянь, обчисленням значень функцій та інтегралів, розв’язуванням трансцендентних та алгебраїчних рівнянь.
Вони відіграють важливу роль у математиці принаймні з двох причин: є ефективним інструментом математичних досліджень і одним із найважливіших засобів побудови практичних чисельних методів.
Широким застосуванням теорії рядів і пояснюється актуальність теми дипломної роботи. Метою роботи є детальне вивчення основних методів підсумовування збіжних та розбіжних рядів.
Теорія рядів почала розвиватися в кінці ХVII ст. але була створена лише в ХІХ ст. на основі поняття границі в роботах Гаусса, Коші. Багато математиків минулого працювали над проблемою знаходження суми ряду. Ейлер в статті «О расходящихся радах» (1754-1755р.) називає ряд збіжним, якщо його члени прямують до нуля, і розбіжним в іншому випадку. Надаючи кожному ряду числове значення, яке Ейлер називає сумою ряду, він підкреслює, що частинні суми не завжди мають точне значення, рівне сумі.
Отже, підсумовувати ряд вдалось в тому випадку, коли ряд збіжний: задача підсумовування зводилась лише до відшукання границі послідовності частинних сум. Що ж стосується розбіжних рядів, то в даному випадку застосування частинних сум не дає бажаного результату. Тому для підсумовування розбіжних рядів необхідно було побудувати іншу теорію.
Поставимо ряду U у відповідність деяке число S(U) , яке будемо називати його сумою. Ми можемо вважати, що маємо справу з функцією S, визначеною для деяких рядів і яка приймає числові значення. Функцію ![]() будемо називати підсумовуючою функцією. Прикладом такої підсумовуючої функції може бути
будемо називати підсумовуючою функцією. Прикладом такої підсумовуючої функції може бути ![]() .
.
Ця функція визначена на множині всіх збіжних рядів, і для кожного збіжного ряду її значення рівне звичайній сумі цього ряду. Так, визначену конкретну підсумовуючу функцію позначимо через ![]()
Можна побудувати надзвичайно велику кількість підсумовуючих функцій. Для виправдання своєї назви вони повинні мати властивості звичайних сум. По-перше, підсумовуюча функція S не повинна суперечити звичайному підсумовуванню збіжних рядів. Іншими словами, якщо U – деякий збіжний ряд, то значення S(U) повинне існувати і бути рівним ![]() . Підсумовуюча функція S , яка має цю властивість, називається регулярною.
. Підсумовуюча функція S , яка має цю властивість, називається регулярною.
По-друге, для будь-яких двох рядів U і V і чисел a і b з існування значень S(U) і S(V) слідує існування значення S(aU+bV) і рівність S(aU+bV)=aS(U) +bS(V).
Підсумовуюча функція, яка має цю властивість називається лінійною.
Наукова робота складається з двох розділів – «Підсумовування збіжних рядів» та «Підсумовування розбіжних рядів». У першому розділі мова йде про збіжні ряди. Розглядаються основні поняття з теорії та подано основні методи підсумовування збіжних рядів: метод Абеля, Ейлера, Кумера та інші. Наводиться ряд прикладів на застосування вказаних методів.
Другий розділ повністю присвячений розбіжним рядам. Тут зясовується суть задачі підсумовування розбіжних рядів, вводиться означення підсумовуючої функції, наводиться ряд способів підсумовування розбіжних рядів, над якими працювали такі вчені як Пуассон, Абель, Чезаро, Ейлер. Також розглядаються інші методи підсумовування розбіжних рядів.
РОЗДІЛ 1.
Підсумовування збіжних рядів
- Основні поняття та означення. Найпростіші властивості числових рядів
Нехай ![]() – деяка послідовність чисел.
– деяка послідовність чисел.
Означення. Числовим рядом називають вираз

Числа ![]() називаються його членами, а
називаються його членами, а ![]() загальним членом.
загальним членом.
Утворимо скінчені суми:
![]()
ці суми називаються частинними сумами числового ряду.
Означення. Якщо існує скінченна границя
![]()
послідовності частинних сум, то ряд (1.1) називається збіжним, а число ![]() вважають його сумою і записують:
вважають його сумою і записують:
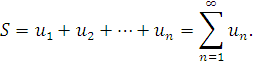
Якщо ж границя (1.2) нескінченна або зовсім не існує, то ряд (1.1) називають розбіжним і вважають, що він суми не має.
Найпростішим прикладом нескінченого ряду є геометрична прогресія
![]()
Її частинна сума буде
![]()
Якщо ![]() , то
, то ![]() має скінченну границю:
має скінченну границю:
![]() , то ряд збігається і
, то ряд збігається і ![]() буде його сумою.
буде його сумою.
Розглянемо деякі властивості збіжних рядів.
- Якщо ряд
![]()
збіжний і має суму ![]() , то ряд
, то ряд
![]()
Також збіжний і сума його дорівнює ![]() . Іншими словами, збіжний ряд можна множити почленно на одне і те саме число.
. Іншими словами, збіжний ряд можна множити почленно на одне і те саме число.
- Збіжні ряди можна почленно додавати та віднімати, тобто якщо ряди
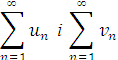
збіжні і мають суми відповідно ![]() та
та ![]() , то збіжними є також ряди
, то збіжними є також ряди
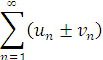
і суми їх дорівнюють ![]() .
.
- На збіжність ряду не впливає відкидання або приєднання до нього скінченної кількості членів.
- (Необхідна умова збіжності ряду.) Якщо ряд
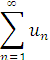
збіжний, то ![]()
При дослідженні на збіжність знакододатних рядів, тобто рядів з невід’ємними членами, найчастіше користуються такими достатніми умовами (ознаками) збіжності, як ознаки порівняння, ознаки Д’Аламбера і Коші та інтегральна ознака Коші.
Теорема1 (ознаки порівняння). Нехай задано два ряди з невід’ємними членами
![]()
![]()
і для всіх ![]() виконується нерівність
виконується нерівність
![]()
Тоді, якщо ряд (1.4) збіжний, то збіжний і ряд (1.3). Якщо ряд (1.3) розбіжний, то розбіжний і ряд (1.4)
Теорема 2 (гранична ознака порівняння). Якщо задано два ряди з додатними членами
![]()
![]()
причому існує скінченна, відмінна від нуля границя
![]()
то ряди або одночасно збіжні, або одночасно розбіжні.
Теорема 3 (ознака Д’Аламбера). Якщо для ряду з додатними членами (1.6) існує границя
![]()
-
ряд збіжний при
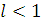 ;
;
-
ряд розбіжний при
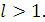
Теорема 4 (ознака Коші) Якщо для ряду (1.6) з додатними членами існує границя
![]()
то цей ряд збіжний при ![]() і розбіжний при
і розбіжний при ![]()
Розглянемо ряд, в яких знаки членів строго чергуються:
![]()
де ![]() . Цей ряд досліджується на збіжність за допомогою такої достатньої ознаки.
. Цей ряд досліджується на збіжність за допомогою такої достатньої ознаки.
Теорема 5 (ознака Лейбніца) Ряд (1.8) збіжний, якщо :
![]()
![]()
При цьому сума ряду додатна і не перевищує першого його члена.
Візьмемо довільний знакозмінний ряд
![]()
де числа ![]() можуть мати довільний знак. Одночасно розглянемо ряд, утворений з модулів ряду (1.11):
можуть мати довільний знак. Одночасно розглянемо ряд, утворений з модулів ряду (1.11):
![]()
Для знакозмінних рядів справедлива така ознака збіжності.
Теорема 6. Якщо ряд (1.12) збіжний, то збіжний і ряд (1.11).
Знакозмінний ряд (1.11) називають абсолютно збіжним, якщо ряд(1.12), утворений з модулів його членів, є збіжним.
Якщо ж ряд (1.11) збіжний, а ряд (1.12), утворений з модулів його членів розбіжний, то ряд (1.11) називають умовно збіжним.
Розглянемо функціональні ряди,тобто ряди членами якого є функції визначені на деякій множині ![]()
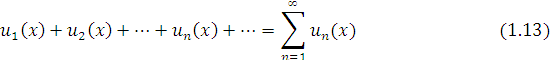
Якщо взяти довільне число ![]() і в ряді (1.13) покласти
і в ряді (1.13) покласти ![]() то дістанемо числовий ряд
то дістанемо числовий ряд
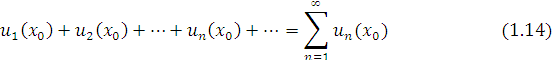
Цей ряд може бути як збіжним, так і розбіжним. Якщо ряд (1.14) є збіжним, то точка ![]() називається точкою збіжності функціонального ряду (1.13). Якщо ж ряд (1.14) є розбіжним, то точка
називається точкою збіжності функціонального ряду (1.13). Якщо ж ряд (1.14) є розбіжним, то точка ![]() називається точкою розбіжності ряду (1.13). Множина всіх точок збіжності функціонального ряду називається областю його збіжності.
називається точкою розбіжності ряду (1.13). Множина всіх точок збіжності функціонального ряду називається областю його збіжності.
Частинна сума функціонального ряду є функцією від ![]() і визначається за аналогією з числовими рядами:
і визначається за аналогією з числовими рядами:
![]()
У кожній точці ![]() , яка належить області збіжності ряду (1.13), існує скінченна границя
, яка належить області збіжності ряду (1.13), існує скінченна границя
![]()
яку називають сумою ряду (1.13) і записують
![]()
Функціональний ряд (1.13) називається рівномірно збіжним на множині ![]() , якщо для довільного
, якщо для довільного ![]() існує таке число
існує таке число ![]() , яке залежить лише від
, яке залежить лише від ![]() і не залежить від
і не залежить від ![]() , що для всіх
, що для всіх ![]() і для всіх
і для всіх ![]() виконується нерівність
виконується нерівність ![]()
Теорема 7 (ознака Вейєрштрасса). Функціональний ряд (1.13) абсолютно і рівномірно збіжний на відрізку ![]() якщо існує знакододатний збіжний числовий ряд
якщо існує знакододатний збіжний числовий ряд

такий що
![]()
- Лінійні перетворення рядів
З’ясуємо збіжність і знайдемо суму ряду
![]()
Зауважимо, що при будь-якому n=1,2,…
![]()
Розглянемо ряд
![]()
Очевидно, для цього ряду
![]()
![]()
![]()
![]()
…………………………..
Для![]() парного:
парного: ![]()
![]()
а для ![]() непарного:
непарного: ![]()
![]()
Звідси видно, що
![]()
ряд (1.18) збігається.
Приклади:
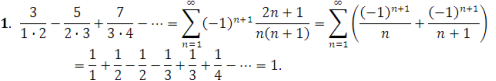
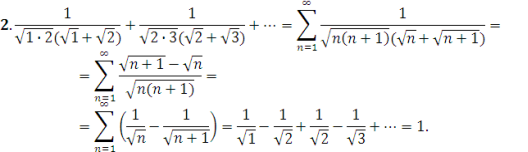
Наступна теорема може розглядатися як узагальнення цього прийому:
Теорема 1. Нехай для ряду
![]() +
+![]() +...+
+...+![]() … (1.19)
… (1.19)
знайдеться така збіжна послідовність ![]() ,
, ![]() , …,
, …,![]() , … із границею T, що для будь-якого цілого додатного q і для всіх n=1, 2, … виконується
, … із границею T, що для будь-якого цілого додатного q і для всіх n=1, 2, … виконується ![]() =
=![]() .
.
Тоді
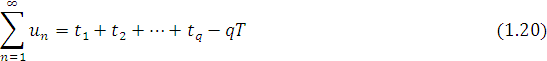
Доведення. Позначивши через ![]() n-ту частинну суму ряду (1.19), для будь-якого n
n-ту частинну суму ряду (1.19), для будь-якого n![]() маємо
маємо
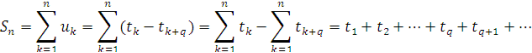
![]() .
.
При необмеженому зростанні n кожна із змінних ![]() за умовою прямує до T, і отримаємо (1.20).
за умовою прямує до T, і отримаємо (1.20).
Приклади:
- Візьмемо довільне ціле додатне q. Тоді для будь-якого α, що не є цілим невід’ємним числом
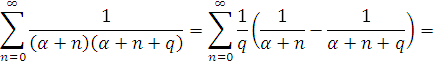

Покладемо
![]()
Очевидно, що
![]()
і застосування доведеної теореми дає
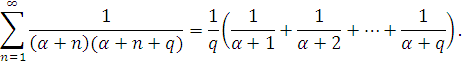
- Для ряду
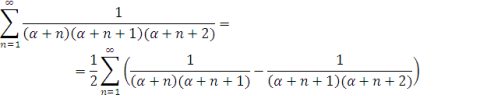
можемо представити
![]()
(очевидно тут при збільшенні n![]() ) а q=1 і одержимо
) а q=1 і одержимо
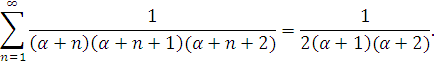
Якщо ![]() то після множення ряду на
то після множення ряду на ![]() отримаємо
отримаємо
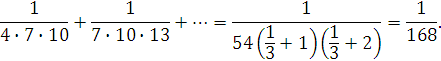
Подальше узагальнення доведеної теореми полягає в наступному:
Теорема 2. Нехай для ряду
![]() +
+![]() +...+
+...+![]() … (1.21)
… (1.21)
знайдеться така збіжна послідовність ![]() ,
, ![]() , …,
, …,![]() , … із границею T, і такі і додатні числа
, … із границею T, і такі і додатні числа ![]() що
що
![]()
і для будь – якого n=1, 2, …
![]() (1.22)
(1.22)
Тоді ряд (1.21) збігається і
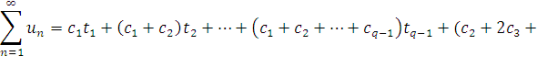
![]()
Доведення. Виразимо всі члени даного ряду (1.21) у вигляді (1.22) і так випишемо ці вирази одне під другим, щоб складові, що містять t з однаковими індексами розташовувались по одній вертикалі для економії місця здійснимо цей запис у формі таблиці 1(числа, які стоять в заголовках стовпців, множаться на всі числа, які стоять у відповідному стовпці і всі такі добутки сумуються). Т1

Суми чисел в кожному із стовпців, які лежать між суцільними вертикальними лініями, рівні нулю, а із зростання n всі числа ![]() прямують до спільної границі T. Звідси випливає (1.23). Зручно користуватись цією теоремою при T=0.
прямують до спільної границі T. Звідси випливає (1.23). Зручно користуватись цією теоремою при T=0.
Приклади:
- Для ряду

маємо
![]()
Тому його сума рівна
![]()
- Для ряду
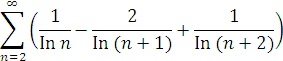
буде
![]()
так, що сума цього ряду буде рівна
![]()
- Сума ряду
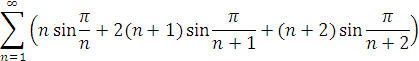
рівна ![]()
4. Сума ряду
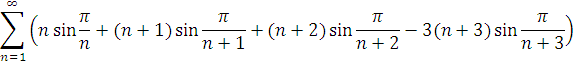
рівна

1.3 Теорема Абеля і почленне диференціювання та інтегрування рядів
Значення суми рівномірно збіжного на деякому проміжку функціонального ряду дозволяє переходити до похідних або до первісних його членів, знаходити суми іншого ряду. Нажаль, не завжди можна скористатись цим способом при обчисленні суми функціональних рядів на межі області їх збіжності. Наступні міркування відкривають в цьому напрямку достатньо широкі перспективи.
Теорема (принцип збіжності) Якщо ![]() - деяка послідовність функцій, то для того, щоб вона рівномірно в області D збігалась до граничної функції
- деяка послідовність функцій, то для того, щоб вона рівномірно в області D збігалась до граничної функції ![]() (x), необхідно і достатньо, щоб для кожного
(x), необхідно і достатньо, щоб для кожного ![]() >0 знайшлося таке n, що для будь-якого т≥
>0 знайшлося таке n, що для будь-якого т≥![]() і для всіх x
і для всіх x![]() D виконувалось
D виконувалось ![]()
Теорема (критерій збіжності) Для того щоб функціональний ряд ![]() збігався рівномірно в деякій області D, необхідно і достатньо, щоб послідовність його частинних сум
збігався рівномірно в деякій області D, необхідно і достатньо, щоб послідовність його частинних сум ![]() мала наступну властивість: яке б не було
мала наступну властивість: яке б не було ![]() існує таке n, що при будь-якого m≥ 0 для всіх x
існує таке n, що при будь-якого m≥ 0 для всіх x ![]() має місце
має місце ![]()
Теорема. Якщо ряд
![]()
збігається, то степеневий ряд
![]()
збігається рівномірно на сегменті ![]()
Доведення. Збіжність ряду (1.24) згідно з критерієм Коші означає, що для будь-якого ![]() знайдеться таке n, що для всіх m
знайдеться таке n, що для всіх m![]() виконується нерівність
виконується нерівність
![]()
Крім того, для будь-якого x![]()
(![]()
Таким чином опинились в умовах леми.
Лема. Якщо послідовність ![]() монотонна і
монотонна і ![]() для всіх
для всіх ![]() то
то ![]()
Ця лема оцінює в даному випадку частинні суми ряду
![]()
тобто ряду
![]()
Ця лема дає
![]()
Оскільки ця оцінка являється рівномірною по x, сформульований вище критерій збіжності Коші стверджує рівномірну збіжність ряду (1.25) на сегменті ![]() Теорема Абеля. Якщо степеневий ряд
Теорема Абеля. Якщо степеневий ряд
![]()
має радіус збіжності R, причому збігається (не обов’язково абсолютно) і при x = R, то збіжність буде рівномірною на всьому сегменті ![]() а сума ряду – неперервною зліва в точці x = R функцією, тобто
а сума ряду – неперервною зліва в точці x = R функцією, тобто

Симетричне твердження має місце у випадку збіжності ряду (1.26) при x = –R.
Доведення. За попередньою теоремою ряд (1.26) збігається на сегменті ![]() рівномірно. Тоді його сума є неперервною функцією від x на всьому сегменті
рівномірно. Тоді його сума є неперервною функцією від x на всьому сегменті ![]() і в частинному випадку має місце (1.27).
і в частинному випадку має місце (1.27).
Приклади:
- Розглянемо, наприклад, розклад в ряд
![]()
Очевидно, ряд який стоїть справа збігається рівномірно при ![]() і тому про інтегрувавши в межах від 0
і тому про інтегрувавши в межах від 0![]() отримаємо
отримаємо
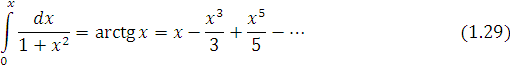
При x =0,1маємо
![]()
Цей ряд – знакозмінний. Тому його залишок не перевищує останнього відкинутого члена. Звідси отримаємо значення
![]()
з п’ятьма знаками.
Ряд при x = 1 збігається,тому згідно доведеної теореми маємо
![]()
- Якщо про інтегрувати ряд
![]()
в межах від ![]() отримаємо
отримаємо
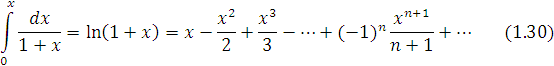
За допомогою цієї формули можна обчислювати логарифм чисел. Обчислимо, наприклад, ![]()
Так як записаний ряд (1.30) збігається і при ![]() ,(за теоремою Абеля) отримаємо
,(за теоремою Абеля) отримаємо
![]()
- Запишемо розклад
![]() ,
,
справедливий для ![]() Інтегруючи його почленно від 0 до деякого x
Інтегруючи його почленно від 0 до деякого x![]() одержимо
одержимо

Ряд, який стоїть справа збігається при x = 1, а інтеграл який стоїть зліва є неперервною функцією своєї верхньої границі. Це дає нам можливість обчислити суму ряду
![]()
Розкладають підінтегральну функцію (1.32) на елементарні дроби
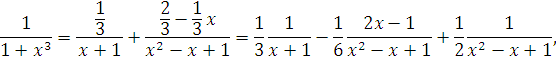
або після перетворення останнього доданку, отримаємо
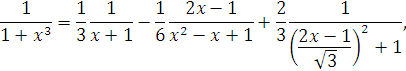
Звідки
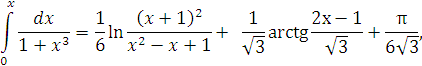
при x = 1, отримаємо
![]()
1.4 Перетворення рядів за Ейлером
Означення. Перетворенням Ейлера називається перехід від ряду

до ряду

Лема. Якщо ряд (1.42) збігається то для будь-якого n =0, 1, 2, …
![]()
Доведення. Оцінимо вираз, який стоїть під знаком границі. Згідно з лемою попереднього пункту маємо
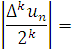

![]()
Зауважимо, що сума всіх коефіцієнтів при модулях тут рівна одиниці, так що сума будь-якого набору цих коефіцієнтів не перевищує одиниці.
Для будь-яких k і ![]() можемо записати
можемо записати
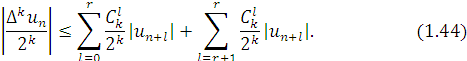
Виберемо тепер довільне ![]() і знайдемо у зв’язку із збіжністю ряду (1.41) таке
і знайдемо у зв’язку із збіжністю ряду (1.41) таке ![]() , що
, що ![]() для всіх
для всіх ![]() . В силу зробленого зауваження про коефіцієнти другий доданок (1.44) справа менший за
. В силу зробленого зауваження про коефіцієнти другий доданок (1.44) справа менший за ![]() .
.
Звернемось до першого доданку. На основі збіжності ряду (1.41) модулі його членів повинні бути обмеженими. Нехай ![]() Далі для довільного
Далі для довільного ![]() маємо
маємо
![]()
Значить
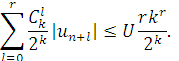
Отже
![]()
(в чому легко переконатися, застосовуючи r раз правило Лопіталя з диференціюванням по k), і тому можна знайти таке k, починаючи з якого
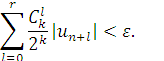
Таким чином, права частина (1.44) із зростання k стає меншою за 2![]() , і нерівність
, і нерівність ![]() доводить наше твердження.
доводить наше твердження.
Теорема. Якщо ряд (1.41) збігається, то одержаний в результаті його перетворення за Ейлером ряд (1.42) також збігається, і їх суми рівні:

Довести цю теорему можна з використанням теорії подвійних рядів, зокрема теореми Маркова.
Приклади:
- Візьмемо ряд
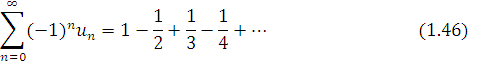
і складемо послідовності його різниць:
![]()
![]()
![]()
![]()
……………………………………
Неважко перевірити, що для ряду (1.46)
![]()
Дійсно будемо доводити методом математичної індукції.
При ![]() це справедливо:
це справедливо:
![]()
Припустивши, що такий вигляд мають ![]() і
і ![]() , ми отримаємо
, ми отримаємо
![]()
так що за означенням (![]() ) –ї різниці
) –ї різниці
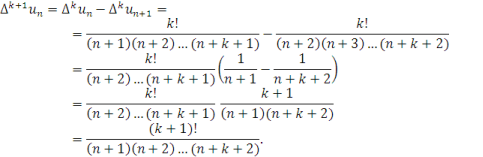
В частинному випадку,
![]()
Звідси випливає, що перетворення Ейлера ряду (1.46) дає
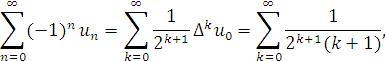
і ми отримаємо рівність
![]()
- Для ряду
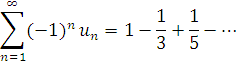
послідовності різниць будуть такі:
![]()
![]()
![]()
![]()
………………….
Припустимо, що тут
![]()
Для перевірки цього припущення методом математичної індукції напишемо
![]()
і складемо різницю
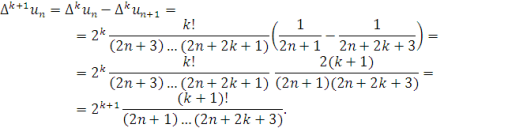
Бачимо, що припущення (1.47) підтвердилось. Відповідно при ![]() маємо
маємо
![]()
Таким чином, перетворення Ейлера дає

Перетворення рядів за Ейлером в багатьох випадках прискорює їх збіжність. Але це справджується не завжди.
- Перетворення рядів за Кумером
Зручно обчислювати значення суми збіжних рядів, використовуючи такі прості міркування. Для знаходження суми ряду можна замінити його іншим рядом із відомою сумою, а потім лише підсумовувати «різницю» між ними. Якщо «різниця» швидко спадає, то й складений із нього ряд буде збігатися досить швидко. Ці міркування запропонував Кумер.
Теорема. Якщо
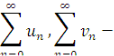
збіжні ряди, причому
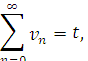
то для будь –якого ![]()
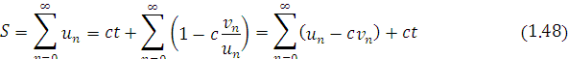
і в частинному випадку, при ![]()
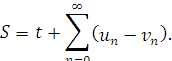
Доведення. Очевидно:

Якщо в умовах даної теореми
![]()
так, що ряд який стоїть в середній частині (1.48) збігається швидше ніж вихідний ряд.
Приклади:
- Для ряду
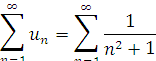
складемо допоміжний ряд з відомою сумою:
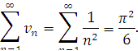
Тут
![]()
Тому
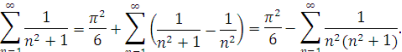
Якщо взяти в перетвореному ряді, наприклад, 9 членів, то похибку можна оцінити так
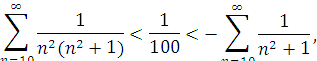
тобто вона в 100 разів менша похибки, одержаної при взяті того ж самого числа членів у вихідному ряді.
- Для ряду
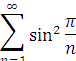
скористаємось тим самим допоміжним рядом « зворотних квадратів». Завдяки тому, що
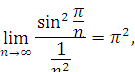
будемо мати
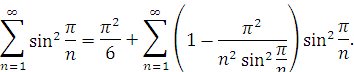
Очевидно, коефіцієнт, який з'являється при членах ряду, спадає приблизно як ![]()
РОЗДІЛ 2. Підсумовування розбіжних рядів
2.1 Підсумовуючі функції
У попередньому розділі для збіжного числового ряду
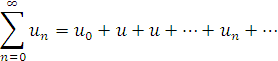
в якості його суми розглядали границю послідовності його частинних сум
![]()
І припускали, що ця границя існує, причому вона скінченна.
Різноманітні факти із області математичного аналізу висунули в другій половині XIX ст. питання про можливість підсумовування розбіжних рядів у деякому новому розумінні. Деякі методи такого «підсумовування» виявилися особливо зручними. Треба сказати, що до створення Коші строгої теорії границь (і зв’язаної з нею теорії рядів) розбіжні ряди нерідко зустрічалися в математичній практиці. Хоча їх застосування при доведеннях часто призводило до суперечок, але тим не менше, робились спроби надавати їм навіть числове значення. Так розбіжному ряду
![]()
ще за часів Лейбніца в якості «суми» приписувалось число ![]() Ейлер, наприклад, мотивував це тим, що із розкладу
Ейлер, наприклад, мотивував це тим, що із розкладу
![]()
(який насправді справедливий лише для ![]() ) при постановці питання не вистачало чіткості, бо довільність у виборі розкладу залишав відкритою можливість із іншого розкладу (де
) при постановці питання не вистачало чіткості, бо довільність у виборі розкладу залишав відкритою можливість із іншого розкладу (де ![]() і
і ![]() довільні,
довільні, ![]() )
)
![]()
отримали одночасно ![]()
Сучасний аналіз ставить питання по іншому. В основу покладемо деяке сформульоване означення «підсумовуючої функції», що стосується цілого класу таких рядів.
Поставимо ряду ![]() у відповідність деяке число
у відповідність деяке число ![]() , яке будемо називати його сумою. Ми можемо вважати, що маємо справу з функцією
, яке будемо називати його сумою. Ми можемо вважати, що маємо справу з функцією ![]() , визначеною для деяких рядів і яка приймає числові значення. Функцію
, визначеною для деяких рядів і яка приймає числові значення. Функцію ![]() будемо називати підсумовуючою функцією.
будемо називати підсумовуючою функцією.
Прикладом такої підсумовуючої функції може бути
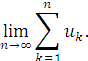
Ця функція визначена на множині всіх збіжних рядів, і для кожного збіжного ряду її значення рівне звичайній сумі цього ряду. Так, визначену конкретну підсумовуючу функцію позначимо через ![]()
Всі підсумовуючі функції, які будемо згадувати далі прийнято зв’язувати із іменами математиків, які їх ввели. Для «звичайної» підсумовуючої функції ![]() цього не роблять. Однак звичайне підсумовування рядів справедливо було б називати «підсумовуванням за Коші».
цього не роблять. Однак звичайне підсумовування рядів справедливо було б називати «підсумовуванням за Коші».
Можна побудувати надзвичайно велику кількість підсумовуючих функцій. Для виправдання своєї назви вони повинні мати властивості звичайних сум.
По-перше, підсумовуюча функція ![]() не повинна суперечити звичайному підсумовуванню збіжних рядів. Іншими словами,якщо
не повинна суперечити звичайному підсумовуванню збіжних рядів. Іншими словами,якщо ![]() – деякий збіжний ряд, то значення
– деякий збіжний ряд, то значення ![]() повинне існувати і бути рівним
повинне існувати і бути рівним ![]() . Підсумовуюча функція
. Підсумовуюча функція ![]() , яка має цю властивість, називається регулярною.
, яка має цю властивість, називається регулярною.
По-друге, для будь-яких двох рядів ![]() і
і ![]() і чисел
і чисел ![]() і
і ![]() з існування значень
з існування значень ![]() і
і ![]() слідує існування значення
слідує існування значення ![]() і рівність
і рівність
![]()
Підсумовуюча функція, яка має цю властивість називається лінійною.
2.2 Підсумовування за Пуассоном-Абелем
Означення. Якщо підсумовуюча функція ![]() визначається рівністю
визначається рівністю
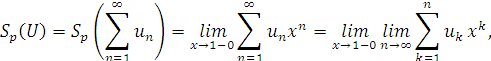
то таке підсумовування називається підсумовуванням за Пуассоном-Абелем.
Приклади:
- Для ряду
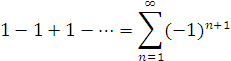
підсумовування за Пуассоном-Абелем дає
![]()
- Розглянемо ряд
![]()
Для нього
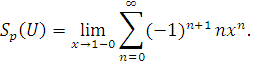
Але для будь-якого ![]() , близького до 1, але меншого за 1, ряд який стоїть під знаком границі збігається. А тому:
, близького до 1, але меншого за 1, ряд який стоїть під знаком границі збігається. А тому:
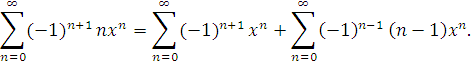
Підсумовуючи ряди які стоять справа, одержимо:
![]()
- Розглянемо ряд
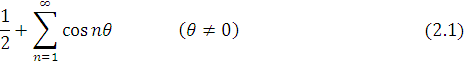
Тут границя
![]()
не існує, тому згідно з необхідною умовою збіжності ряду (2.1) розбігається.
Підсумуємо цей ряд за Пуассоном-Абелем. Для цього візьмемо довільне ![]() розглянемо ряд
розглянемо ряд

і складемо ряд з модулів членів цього ряду:
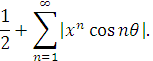
Ознака збіжності Коші дає нам, що
![]()
Отже останній ряд збігається. Це означає, що ряд (2.2) збігається абсолютно, а тому – збігається. Знайдемо його суму.
Зазначимо, що ![]() дійсна частина комплексного числа
дійсна частина комплексного числа ![]()
Тому
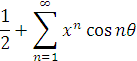
є дійсною частиною виразу
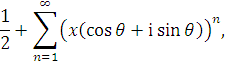
Або, підсумовуючи дану геометричну прогресію, отримаємо
![]()
Множення чисельника і знаменника цього дробу на комплексне число, спряжене знаменнику, дає нам

Після очевидних обчислень виявляється, що дійсна чистина цього виразу рівна
![]()
Таким чином (підкреслимо, що припускаємо ![]()
![]()
2.3 Лінійність та регулярність підсумовування за Пуассоном-Абелем
Лінійність підсумування за Пуассоном-Абелем випливає із того, що для будь-яких рядів ![]() і
і ![]()
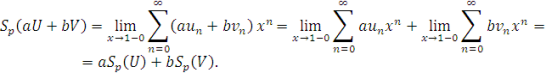
Встановимо регулярність цього підсумовування.
Теорема. Якщо ![]() збіжний ряд, то він підсумовується за методом Пуассона-Абеля і
збіжний ряд, то він підсумовується за методом Пуассона-Абеля і ![]()
Доведення. Складемо за рядом ![]() степеневий ряд
степеневий ряд

Із збіжності ряду ![]() випливає, що радіус збіжності степеневого ряду (2.4) не менше одиниці, причому при
випливає, що радіус збіжності степеневого ряду (2.4) не менше одиниці, причому при ![]() цей ряд збігається. Тому в другій теоремі Абеля сума ряду (2.4) неперервна в точці
цей ряд збігається. Тому в другій теоремі Абеля сума ряду (2.4) неперервна в точці ![]() зліва, тобто
зліва, тобто
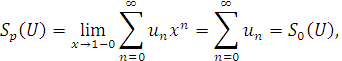
теорему доведено.
2.4 Абсолютна збіжність методу Пуассона - Абеля
Ряд (1.2) називається підсумовуваним методом Пуассона-Абеля (А – підсумовуваним до числа ![]() ), якщо степеневий ряд
), якщо степеневий ряд![]() , збігається при
, збігається при![]() і
і ![]() [1, 45].
[1, 45].
Переформулюємо означення: послідовність ![]() називається А – підсумовуваною до числа
називається А – підсумовуваною до числа ![]() , якщо степеневий ряд
, якщо степеневий ряд ![]() збігається при
збігається при ![]() , і
, і![]() .
.
Метод А – напівнеперервний метод підсумовування, де
![]() ,
,![]() .
.
Ряд (1.2) називається абсолютно підсумовуваним методом Пуассона-Абеля (![]() – підсумовуваним), якщо функція
– підсумовуваним), якщо функція ![]() має обмежену зміну на сегменті
має обмежену зміну на сегменті![]() , або
, або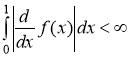 [13, 14, 23].
[13, 14, 23].
Так, наприклад,
1). ряд ![]() не є А – підсумовуваним, оскільки
не є А – підсумовуваним, оскільки![]() , при
, при ![]() ;
;
2). ряд ![]() не є А – підсумовуваним, оскільки степеневий ряд
не є А – підсумовуваним, оскільки степеневий ряд ![]() розбігається при
розбігається при ![]() .
.
3). ряд![]() є А – підсумовуваним до суми
є А – підсумовуваним до суми ![]() , оскільки
, оскільки![]() при
при ![]() .
.
Теорема1.41. Метод ![]() є регулярним.
є регулярним.
Теорема1.42. Метод ![]() зберігає абсолютну збіжність.
зберігає абсолютну збіжність.
Теорема1.43. Якщо ![]() , то
, то ![]() і обидва методи сумісні.
і обидва методи сумісні.
Для![]() отримуємо: якщо
отримуємо: якщо ![]() , то
, то ![]() .
.
Підсумовуваність та абсолютна підсумовуваність методом Пуассона-Абеля мають велике значення в теорії рядів Фур’є [20].
Різниця між абсолютною збіжністю ряду і його умовною збіжністю з точки зору підсумовування за Пуассоном-Абелем зберігається, наприклад, ряд
![]()
за Пуассоном-Абелем підсумовуємо, але ряд, який складається із модулів його членів, тобто ряд
![]()
ні. Тут ця різниця виявляється слабшою, ніж у випадку звичайної збіжності.
Означення. Нехай нам дано ряди ![]()
Добутком цих рядів будемо називати ряд ![]() в якому
в якому
![]()
Для абсолютно збіжних рядів ![]() має місце наступна рівність
має місце наступна рівність
![]()
Якщо ж обидва ряди ![]() збігаються, але лише умовно, то це очевидне на перший погляд співвідношення не виконується (втрачає зміст його перша частина).
збігаються, але лише умовно, то це очевидне на перший погляд співвідношення не виконується (втрачає зміст його перша частина).
Наприклад. Нехай кожен із рядів ![]() є
є
![]()
Тоді для члена ![]() ряду
ряду ![]() , який є добутком
, який є добутком ![]() маємо:
маємо:
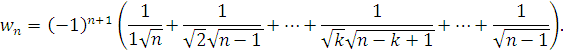
Внаслідок того, що
![]()
тут повинно бути
![]()
тобто ряд ![]() не задовільняє необхідну умову збіжності, і сума
не задовільняє необхідну умову збіжності, і сума ![]() не існує.
не існує.
Однак з точки зору підсумовування за Пуассоном-Абелем різниця в цьому питанні між абсолютною і умовною збіжністю втрачається.
Теорема. Якщо ряди ![]() підсумовувані за Пуассоном-Абелем, то їх добуток
підсумовувані за Пуассоном-Абелем, то їх добуток ![]() також підсумовуємо за Пуассоном-Абелем, і
також підсумовуємо за Пуассоном-Абелем, і
![]()
Доведення. Підсумовування рядів ![]() ,за теоремою Пуассона-Абеля означає збіжність степеневих рядів
,за теоремою Пуассона-Абеля означає збіжність степеневих рядів
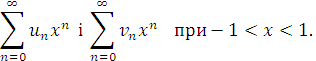
Звідси, за теоремою Абеля кожен такий ряд збігається, причому абсолютно. Але тоді за теоремою про множення абсолютно збіжних рядів
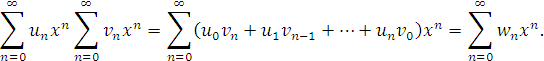
Ліва частина цієї рівності за умовою при ![]() має границю рівну добутку
має границю рівну добутку ![]() Значить, і права його частина має границю, яка за означенням дорівнює
Значить, і права його частина має границю, яка за означенням дорівнює ![]()
Таким чином, з точки зору множення радів підсумовування рядів за Пуассоном – Абелем навіть «ближче» до скінченних сум ніж підсумовування рядів у звичайному розумінні.
Приклади:
-
Нехай обидва ряди
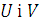 є одним і тим же рядом
є одним і тим же рядом
![]()
тобто ![]() Тоді
Тоді ![]() тобто ряд
тобто ряд
![]()
![]()
Тому за тільки що доведеною теоремою
![]()
- Розглянемо ряд
![]()
Він не збіжний навіть умовно, оскільки
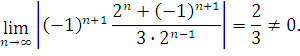
Однак цей ряд може бути отриманий в результаті перемноження ряду
![]()
і геометричної прогресії
![]()
В нашому випадку
![]()
і підсумовування скінченної геометричної прогресії, яка стоїть у дужках дає можливість знайти ![]()
Нагадаємо, що сума ряду (2.7) за Пуассоном-Абелем рівна ![]() , а прогресія (2.8) збігається в звичайному розумінні (а значить і за Пуассоном – Абелем) і має суму рівну 2.
, а прогресія (2.8) збігається в звичайному розумінні (а значить і за Пуассоном – Абелем) і має суму рівну 2.
Звідси ряд (2.6) також збігається за Пуассоном – Абелем і його сума дорівнює ![]()
2.5 Теорема Таубера
В результаті різного роду перетворень, зокрема, в результаті переходів від одних рядів до інших, можемо отримати ряди сумовні за Пуассоном-Абелем. Прикладом їх можуть бути розглянуті в попередньому параграфі добутки рядів. У всіх потрібних випадках може викликати інтерес з’ясування збіжності цих рядів у звичайному розумінні.
Таким чином, виникає питання про ознаки збіжності спеціально для тих рядів які є сумовними за Пуассоном-Абелем. Ці ознаки, які відносяться до рядів, що підсумовуються за Пуассоном-Абелем, так і до рядів, що підсумовуються будь-яким іншим методом, зазвичай називаються тауберовими теоремами. Історично перша з них, належить самому Тауберу, полягає в наступному
Теорема Таубера. Для того, щоб сумовний за Пуассоном – Абелем ряд
![]()
що має суму ![]() , збігався в звичайному розумінні ( і мав суму
, збігався в звичайному розумінні ( і мав суму![]() ) необхідно і достатньо щоб виконувалось граничне відношення
) необхідно і достатньо щоб виконувалось граничне відношення
![]()
Частинну теореми Таубера, яка стосується необхідності, виділимо як самостійну лему.
Лема. Якщо збігається ряд (2.9) то має місце (2.10).
Доведення. Нехай ряд (2.9) збігається і ![]() -тий його залишок. Збіжність ряду означає, що
-тий його залишок. Збіжність ряду означає, що
![]()
Далі маємо
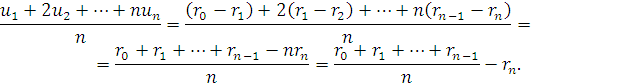
Таким чином,
![]()
За (2.11) друга границя справа тут рівна нулю. Якби перша границя не існувала або була відмінна від нуля, то знайшлося б таке ![]() що при як завгодно великих значеннях
що при як завгодно великих значеннях ![]() виконувалася б нерівність
виконувалася б нерівність
![]()
Знайдемо тепер у відповідності із збіжністю ряду (2.9) таке ![]() , що при
, що при ![]()
![]()
а за ним – таке ![]() , що
, що

Число ![]() можна брати скільки завгодно великим. Візьмемо його таким, щоб було одночасно
можна брати скільки завгодно великим. Візьмемо його таким, щоб було одночасно
![]()
Запишемо
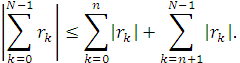
Із (2.14) випливає, що тут перший доданок менший ніж ![]() Із (2.13) випливає що другий доданок менший за
Із (2.13) випливає що другий доданок менший за ![]() Значить, з урахуванням (2.15)
Значить, з урахуванням (2.15)
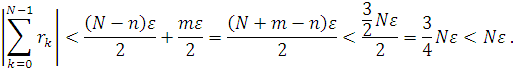
А це суперечить (2.12), лема доведена.
Переходимо до доведення достатності. Почнемо з того частинного випадку, коли члени ряду (2.9) спадають настільки швидко, що
![]()
Покладемо
![]()
Із (2.16) випливає, що із збільшення ![]() величина
величина ![]() монотонно прямує до нуля.
монотонно прямує до нуля.
Візьмемо довільне ![]() і запишемо
і запишемо
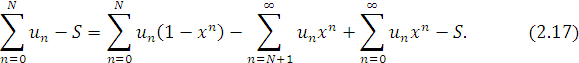
Зауважимо, що при ![]() повинно бути
повинно бути
![]()
і 
Користуючись цими оцінками і властивостями ![]() можемо оцінити перші два доданки в (2.17) справа:
можемо оцінити перші два доданки в (2.17) справа:
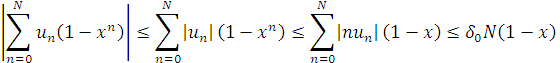
і
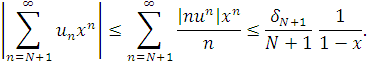
Тому із (2.17) випливає, що
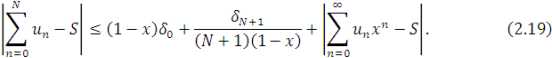
Візьмемо довільне ![]() і виберемо
і виберемо ![]() так, щоб було
так, щоб було ![]() тобто
тобто ![]() Візьмемо тепер
Візьмемо тепер ![]() настільки великим, щоб виконувалась нерівність
настільки великим, щоб виконувалась нерівність
![]()
а ![]() залежне від
залежне від ![]() настільки близько до одиниці, щоб виконувалась нерівність
настільки близько до одиниці, щоб виконувалась нерівність
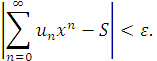
Тоді в (2.19) ліва частина може бути оцінена як
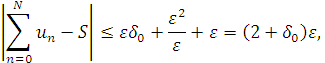
і довільність ![]() доводить збіжність ряду (2.9). Виділені умовами (2.16) частинний випадок доведений. Розглянемо тепер загальний випадок. Покладемо
доводить збіжність ряду (2.9). Виділені умовами (2.16) частинний випадок доведений. Розглянемо тепер загальний випадок. Покладемо
![]()
і (умовно) ![]() Тоді, при
Тоді, при ![]()
![]()
так що
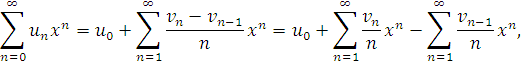
або,пересунувши на одиницю нумерацію у другій сумі справа, маємо
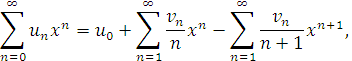
звідси
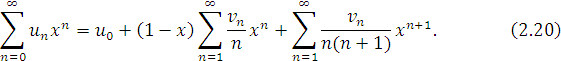
Розглянемо тепер вираз
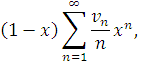
який представимо у вигляді
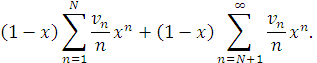
Візьмемо тут довільне ![]() і виберемо у відповідності до (2.10)
і виберемо у відповідності до (2.10) ![]() настільки великим, щоб при
настільки великим, щоб при ![]() було
було 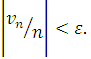 В цьому випадку з урахуванням (2.18) для будь-якого
В цьому випадку з урахуванням (2.18) для будь-якого ![]() буде
буде
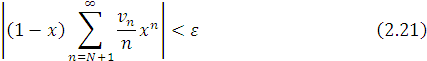
Далі, наближаючи ![]() до одиниці можемо отримати
до одиниці можемо отримати
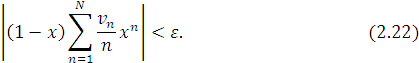
Враховуючи (2.21) і (2.22) отримаємо, що при значеннях ![]() достатньо близьких до одиниці
достатньо близьких до одиниці
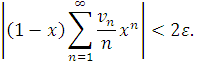
Звідси випливає (оскільки ліва частина цієї нерівності не залежить від ![]() що
що
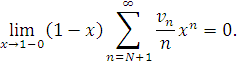
з рівності (2.20) отримаємо
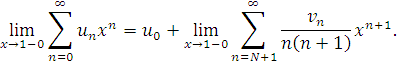
Але за умовою підсумовування рядів ліва частина рівна тут ![]() Тому
Тому
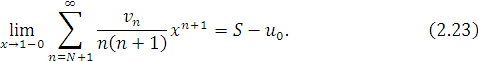
Розглянемо тепер допоміжний ряд
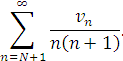
Для нього маємо згідно (2.10)
![]()
Тому опиняємось в умовах уже розглянутого частинного випадку. Тим самим від (2.23) можемо перейти до рівності

Нарешті маємо для будь-якого ![]()

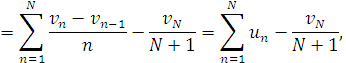
звідси
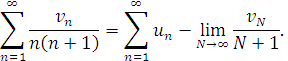
Тут границя справа за умовою рівна нулю, і з (2.24) маємо

Таким чином, ряд (2.9) збігається і його сума рівна ![]()
Для методів Чезаро найбільш типовою формою умови ![]() (що допускає різні узагальнення) є
(що допускає різні узагальнення) є ![]() [23, 28, 80].
[23, 28, 80].
Теорема 2.1.Якщо![]() для деякого
для деякого![]() і
і![]() ,то ряд
,то ряд![]() збігається і є сумованим
збігається і є сумованим![]() для будь-якого додатного
для будь-якого додатного


про публікацію авторської розробки
Додати розробку
