Математичний захід " Доторкнутися до нескінченності"

Математичний захід: « Доторкнутися до нескінченності»

      Нещодавно при розмові з мамою я почув дивну фразу: гомоморфний образ групи ізоморфний фактор-групі по ядру гомоморфизму. Виявилося, що це теорема з такою незвичайною науки як топологія. Мені захотілося дізнатися більше про цю специфічну науку й ми з однокласниками почали працювати над цією темою.

 

Мета: донести до людей інформацію про топологію і зацікавити їх цією наукою.

Завдання: 1. Вивчити основні поняття топології.

                   2. Продемонструвати односторонні поверхні.

                   3. Показати те, що топологія цікава і навіть актуальна наука.

 

 

1. Що таке геометрія
2. Основні поняття топології
3. Властивості топології
4. Відкриття Мебіуса
5. Пляшка Клейна
6. Топологічна людина
7. Топологія у житті
8. Застосування листа Мебіуса
9. Висновок

 

 

Що таке геометрія

 

      Слово «геометрія» в перекладі з давньоєгипетського означає «землевимір».

Початкові геометричні поняття виникли у людей в часи глибокої давнини, коли люди оцінювали відстані, робили прямі списи і стріли, порівнювали їх по довжині і т.п. Потім з розвитком землеробства були вироблені в практиці правила і способи вимірювання земельних ділянок, правила знаходження найпростіших площ і обсягів, правила, необхідні для будівництва. Наприклад, в Давньому Єгипті для розмітки земельних ділянок використовували кілочки з натягнутою між ними мотузкою і трикутники, зроблені з паличок, щоб відкладати рівні кути.

     У ті далекі часи геометрія була досить розвинена: стародавні люди могли приблизно знаходити площу кола, об'єм кулі, вирішувати досить складні геометричні завдання. На практиці була виведена, але ще не доведена теорема Піфагора. Геометричні знання активно використовувалися при будівництві будівель і храмів.

     Як наука геометрія з'явилася в Греції в період з VII по V ст. до н.е. Першими філософами-геометрами прийнято вважати Фалеса і Піфагора.

Основні досягнення грецької геометрії до 300 р до н.е. були викладені Евклидом в його знаменитій праці «Начала». Там містяться тільки основи геометрії того часу. «Начала» складаються з 13 книг, або глав. У кожній з них містяться визначення. Ось деякі з них:

1. Точка є те, що не має частин.

2. Лінія - довжина без ширини.

3. Кінці лінії - точки.

4. Поверхня є те, що має тільки довжину і ширину.

     Далі наведені постулати і аксіоми - положення, що приймаються без доказів.

     Праця Евкліда містить відомості в області планіметрії (геометрія на площині), стереометрії (геометрія в просторі), теорії чисел.

«Начала» служили зразком наукового викладу протягом двох тисяч років. З часів Евкліда все вивчали геометрію по його «Початкам».

      У XVII ст.н.е. в Індії, в Середній Азії, в арабських країнах і Європі геометрія отримала значний розвиток, були створені нові теорії, нові методи.

      Пізніше, в XIX столітті, деякі вчені в різних країн прийшли до висновку про існування іншої, неевклідової геометрії, де не діють звичні затвердження Евкліда. З'явилася так звана «геометрія Лобачевського», геометрія на викривлених поверхнях. Так, наприклад, якщо намалювати трикутник на увігнутій поверхні, то сума його кутів не дорівнюватиме 180 градусам

 

 

          

 

 

 

 

 

 

 

 

 

 

    

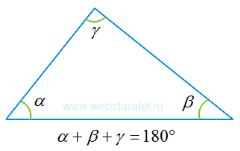
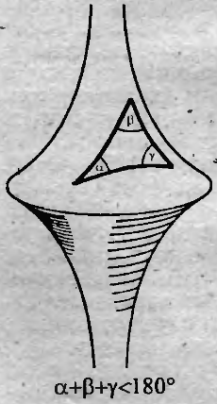
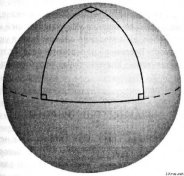
      На сфері «трикутник» може мати три прямих кута.

Згодом були запропоновані й інші моделі геометрії Лобачевського. Тим самим було показано, що геометрія Евкліда не є єдино можливою. Це мало великий прогресивний вплив на весь подальший розвиток геометрії і математики в цілому.

      А в XX в. було виявлено, що геометрія Лобачевського не тільки має важливе значення для абстрактної математики, а й пов'язана з фізикою. Виявилося, що взаємозв'язок простору і часу, відкрита в роботах X. Лоренца, А. Пуанкаре, А. Ейнштейна, Г. Маньківського, має безпосереднє відношення до геометрії Лобачевського.

Наприклад, в розрахунках сучасних синхрофазотронів використовуються формули геометрії Лобачевського.

     З середини XIX століття стала виділятися область геометрії, що досліджує властивість фігур при безперервних перетвореннях - топологія.

Топологія - досить складна наука. Вона вимагає знання геометрії, алгебри та інших розділів математики, а також уміння міркувати. Але я постараюся розповісти про топології простою мовою.

 

 

                                         Основні поняття топології

 

Зараз ми поговоримо про бублик!

Напевно, Ви здивуєтеся: причому тут бублики? Насправді, одне з основних понять топології - тор, або бублик.

Ця фігура отримана шляхом обертання кола навколо осі, яка не перетинає коло.

 

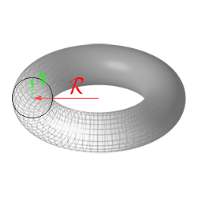
А тепер подумайте, що може пов'язувати тор і звичайну кружку?

 

 

 

    Топологія розглядає перетворення фігур. Для цього використовується наступне визначення.

      Гомеоморфізм - це перетворення фігур, що має певні властивості:

неорієнтовність ( однобічність), взаємо-однозначністю і неперервністю.

Будемо вважати, що ми працюємо з пластиліновими фігурками, і пластилін можемо розтягувати, стискати, при цьому заборонені склеювання різних точок і розриви. Геометричні фігури, що переходять одна в іншу при топологічних перетвореннях, називаються гомеоморфними.

 

Властивості топології

     1)Неорієнтовність (однобічність). Такі поверхні, як сфера, тор і неперекрученная стрічка, називають орієнтовними або двосторонніми.

А сьогодні ми поговоримо про неорієнтовні поверхні, але це згодом.

 

      2) Неперервність- ще одне топологічна властивість. Тополог може як завгодно деформувати предмети, аби точки, які раніше були сусідами, залишалися одна біля одної і далі.

Наприклад, коло і границя квадрата гомеоморфні, оскільки їх можна перевести один в одного топологічним перетворенням (тобто згинанням і розтягуванням без розривів і склеювання).

Це легко уявити собі за допомогою замкнутої мотузочки - з неї можна викласти коло, і перетворити її в квадрат, і назад.

У науково-популярній літературі топологію часто називають "геометрією на гумовому аркуші", оскільки її наочно можна уявляти собі як геометрію фігур, намальованих на пружних гумових листах, які піддаються розтягування, стиснення або вигинанню.

Тепер ми можемо зрозуміти, що коло не відрізняється від квадрата або трикутника, тому що їх легко перетворити один в інший, не порушуючи безперервності й

поверхня куба гомеоморфна сфері. Якщо ми деформуємо куб, то можна отримати кулю.

 

 

 

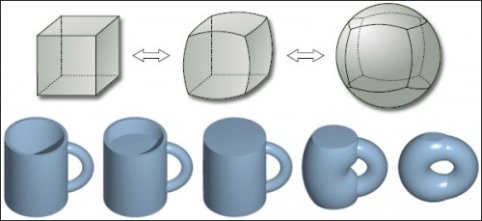
     3) Але куди цікавіше інша властивість - зв'язність.

Повернемося до нашої кружки. З боку топології кружка  і тор- це одне і те ж. Кружка гомеоморфна тору. Тобто можна "надути" кружку і отримати бублик, а потім здути його. Ми бачимо, що кружка безперервними деформаціями переходить в тор. Зауважимо, що при таких деформаціях одне залишається незмінним - наявність «дірки». В даному випадку «дірка» одна.

Але з тора зробити кулю неможливо, так як буде заважати отвір в центрі.

З тора можна отримати так звану сферу з ручкою. Прекрасним прикладом сфери з ручкою є спортивна гиря.

Можна уявити собі сферу з безліччю ручок. З такими поняттями працює топологія.

 

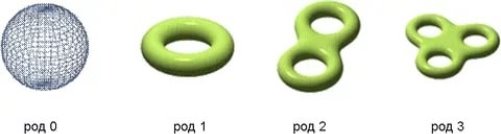
Наявність або відсутність «дірок» є топологічною властивістю, вона зберігається при топологічному перетворенні, як в нашому прикладі з кружкою. Область з діркою не може перейти при гомеоморфізмі в область без дірок. У топології використовується таке поняття, як рід. Говорячи зовсім простою мовою, можна визначити рід як кількість «дірок». Таким чином, рід сфери дорівнює нулю, рід тора (поверхні "бублика") - одиниці, рід кренделя (тора з двома дірками) - двом, рід поверхні з p дірами дорівнює p. Звідси випливає, що ні поверхню куба, ні сфера не гомеоморфні тору.

 

 

 

Чому розглядається саме сфера з ручками? Все дуже просто - будь-яка фігура гомеоморфна сфері з деякою кількістю ручок. Будь-який об'ємний предмет, влаштований як сфера з деякою кількістю ручок. Будь то чашка, ложка, комп'ютерна миша, людина.

     4) І, нарешті, те, що зветься "хроматичний номер". Він дорівнює максимальному числу областей, які можна намалювати на поверхні так, щоб кожна з них мала спільний кордон з усіма іншими. Якщо кожну таку область пофарбувати по-різному, то будь-який колір повинен бути сусідом з будь-яким іншим. Так ось, на аркуші паперу, навіть якщо його склеїти в кільце, ще нікому не вдалося розташувати п'ять кольорових плям будь-якої форми, які мали б загальний кордон. І на сфері, і на циліндрі їх може бути не більше чотирьох. Це і означає що хроматичний номер цих поверхонь - чотири. А на бублику число відповідних кольорів дорівнює семи.

 

                                                 Відкриття Мебіуса

     Ця історія сталася в 1863 році. У кріслі сидів чоловік. Думки були різні, але якось нічого особливого не спадало на думку. Тільки в повітрі витало відчуття, що саме цей день принесе славу і увічнить ім'я Августа Фердинанда Мебіуса. На порозі кімнати з'явилася кохана дружина. Правда, вона була не в доброму гуморі. Правильніше сказати, вона була розгнівана, і вимагала негайно звільнити служницю, яка настільки бездарна, що навіть не здатна правильно зшити стрічку. Похмуро розглянувши злощасну стрічку, професор вигукнув: "Ай да, Марто! Дівчинка не так вже дурна. Адже це ж одностороння кільцева поверхню. У стрічки немає вивороту! "

     Багато хто вважає, що лист Мебіуса є прабатьком символу нескінченності. Однак за наявними історичними відомостями символ нескінченності став використовуватися для позначення нескінченності за два століття до відкриття стрічки Мебіуса.

     Найпростішою односторонньої поверхнею є лист Мебіуса, який отримав свою назву на честь А. Мебіуса, який відкрив його надзвичайні топологічні властивості. Якщо смужку паперу перед склеюванням  перекрутити на півоберта і склеїти точку A з точки C, а B з D, то вийде лист Мебіуса. У цієї фігури є тільки одна поверхню і один край. Жук, що повзе по середині аркуша Мебіуса (не перетинаючи краю), повернеться в початкову точку в положенні "догори ногами". При розрізуванні листа Мебіуса по середньої лінії він не розпадається на дві частини.

 

 

 

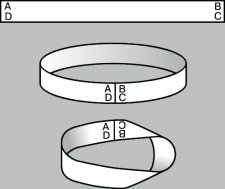
                                                  Пляшка Клейна

          У 1882 році ще одну однобічну поверхню побудував німецький математик Фелікс Клейн. Ця поверхня є не тільки односторонній, але і замкнутой.  В математиці Пляшка Клейна – це певна неоріентовна поверхню роду 1, тобто поверхня (двовимірний топологічний простір), у якій немає різниці між внутрішньою і зовнішньою сторонами. Пляшка Клейна тісно пов'язана зі стрічкою. Щоб зробити пляшку Клейна, необхідно взяти пляшку з отвором в денці, витягнути шийку, зігнути її вниз, і протягнувши її через отвір в стінці пляшки (для справжньої пляшки Клейна в чотиривимірному просторі цей отвір не потрібно, але без нього не можна обійтися в тривимірному евклідовому просторі ), приєднати до отвору на дні пляшки.

 

       На відміну від звичайної склянки у цього об’єкта немає «краю», де б поверхню різко закінчувалася. На відміну від повітряної кулі можна пройти шлях зсередини назовні не перетинаючи поверхню (тобто насправді у цього об’єкта немає «всередині» і немає «зовні»). Назва, очевидно, походить від неправильного перекладу німецького слова Flache (поверхню), яке в німецькій мові близько за написанням до слова Flasche (пляшка). При розтині пляшки Клейна виходить стрічка Мебіуса (рис.2). На рис.3 представлена ​​розгортка пляшки Клейна.
       Подібно стрічці Мебіуса, пляшка Клейна є двовимірним диференційовним неоріентовним різноманіттям. На відміну від стрічки Мебіуса, пляшка Клейна є замкнутим різноманіттям, тобто компактним різноманіттям без краю. – Пляшка Клейна не може бути вкладена (тільки занурена) в тривимірний евклідів простір, але вкладається в чотиривимірний неевклидовий.

Пляшка Клейна може бути отримана склеюванням двох стрічок Мебіуса по краю.

-Якщо розрізати пляшку Клейна навпіл уздовж її осі симетрії, то результатом буде стрічка Мебіуса.

Якщо пустити жука в отвір у основі пляшки, то він скоро вповзе в порожнину пляшки вже всередині. Жук звідси зможе виповзти назовні і вповзти туди, звідки почав свій шлях.

 

 

Топологічна людина

     Безперервними деформаціями людина може розплутати пальці - факт. Не відразу очевидно, але можна здогадатися.

А якщо ж наша топологічна людина завбачливо надіне годинник на одну руку, то наше завдання стане нездійсненним.

 

 

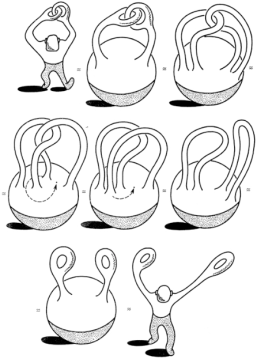
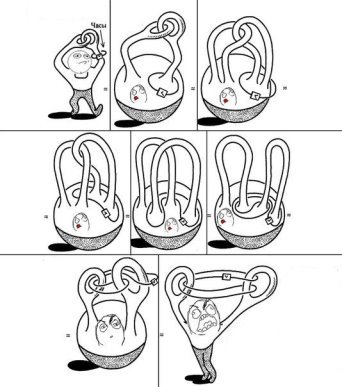
Чи зможете ви розчепити ці кільця, не розтуляючи при цьому пальців?

Здавалося б, будь-яка людина при здоровому глузді скаже: "Звичайно ж, ні!", Але математик відповість інакше ... Спробуємо зрозуміти і математика. Для цього потрібно уявити собі, що наш піддослідний зі зчепленими пальцями може зазнавати топологічні зміни - як завгодно розтягуватися і стискатися, змінювати форму - така собі амеба. Тоді, виявляється, все можливо!

                                                       Топологія у житті

 

    

 

 

 

 

 

 

 

 

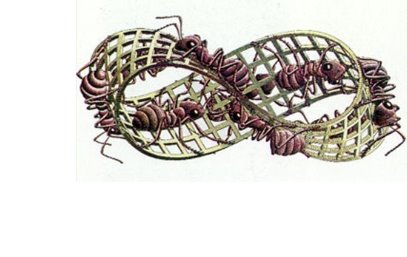
      Лист Мебіуса служив натхненням для скульптур і для графічного мистецтва. Ешер був одним з художників, хто особливо любив його і присвятив кілька своїх літографій цьому математичного об'єкту.

      Лист Мебіуса є символом серії науково-популярних книг «Бібліотечка Квант». Він також постійно зустрічається в науковій фантастиці, наприклад в оповіданні Артура Кларка «Стіна Темряви». Іноді науково-фантастичні розповіді (слідом за фізиками-теоретиками) припускають, що наш Всесвіт може бути деяким узагальненим листом Мебіуса.

Також стріска Мебіуса постійно згадується в творах  письменника Владислава Крапівіна, цикл «В глибині Великого Кристалу» (наприклад «Застава на якірних Поле. Повість»). В оповіданні «Лист Мебіуса» автора А. Дж. Дейча, бостонське метро будує нову лінію, маршрут якої стає настільки заплутаним, що перетворюється в стрічку Мебіуса, після чого на цій лінії починають зникати поїзда. За мотивами оповідання був знятий фантастичний фільм «Мебіус» режисера Густаво Москера. Також ідея стрічки Мебіуса використовується в оповіданні М. Кліфтона «На стрічці Мебіуса».

      Стрічка Мебіуса використовується як спосіб переміщення в просторі і часі Гаррі Кифа, головного героя роману Брайана Ламлі «Некроскоп».

Стрічка Мебіуса грає важливу роль у фантастичному романі Р. Желязни "Двері в піску".

      З стрічкою Мебіуса порівнюється протягом роману сучасного російського письменника Олексія Шепелёва «Echo». З анотації до книги: «Echo» - літературна аналогія кільця Мебіуса: дві сюжетні лінії - «хлопчиків» і «дівчаток» - переплітаються, перетікають одна в одну, але не перетинаються ».

 

Застосування листа Мебіуса

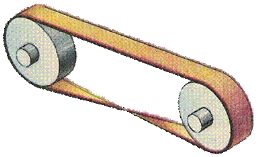
     Стрічка Мебіуса використовується в багатьох винаходи, навіяних ретельним вивченням властивостей односторонньої поверхні. Властивості однобічності листа Мебіуса було використано в техніці: якщо у пасової передачі ремінь зробити у вигляді листа Мебіуса, то його поверхня буде зношуватися вдвічі повільніше, ніж у звичайного кільця. Це дає відчутну економію.

     Пристрій під назвою резистор Мебіуса - це недавно винайдений електронний елемент, який не має власної індуктивності. Нікола Тесла запатентував подібний пристрій. Котушка для електромагнітів призначалася для використання в його системі глобальної передачі електрики без дротів.

 

     Магнітофонний стрічка, розташована в касеті по стрічці Мебіуса, програватиметься в два рази довше. Також в системах запису на безперервну плівку застосовувалися стрічки Мебіуса (щоб подвоїти час запису). А років вісімнадцять тому стрічці знайшли зовсім інше застосування - вона стала грати роль пружини, ось тільки пружини особливою. Як відомо стиснута пружина спрацьовує в протилежному напрямку. Стрічка Мебіуса ж, зневаживши всі закони, напрямку спрацьовування не змінює, подібно механізмам з двома стійкими положеннями. Така пружина могла б стати безцінною в заводних іграшках - її не можна перекрутити, як звичайну - свого роду вічний двигун.

     Є гіпотеза, що спіраль ДНК сама по собі теж є фрагментом стрічки Мебіуса і тільки тому генетичний код такий складний для розшифровки і сприйняття. Більше того - така структура цілком логічно пояснює причину настання біологічної смерті - спіраль замикається сама на себе і відбувається самознищення.

     Фізики стверджують, що всі оптичні закони засновані на властивостях стрічки Мебіуса, зокрема відображення в дзеркалі - це своєрідний перенос в часі, короткостроковий, що триває соті частки секунди, адже ми бачимо перед собою дзеркального свого двійника.

      Стрічка Мебіуса сподобалася не тільки математикам, а й фокусникам. Понад 100 років стрічка Мебіуса використовується для показу різних фокусів і розваг.

Дивовижні властивості листа демонструвалися навіть в цирку, де подвешивались яскраві стрічки, склеєні у вигляді листів Мебіуса. Фокусник закурював сигарету і палаючим кінцем доторкався до середньої лінії кожної стрічки, яка була виконана з калійної селітри. Вогняна доріжка перетворювала першу стрічку в довшу, а другу - в дві стрічки, протягнута одна в іншу. (В цьому випадку фокусник розрізав лист Мебіуса не посередині, а на відстані в одну третину його ширини).

      Лист Мебіуса служив натхненням для скульптур і для графічного мистецтва. Ешер був одним з художників, хто особливо любив його і присвятив кілька своїх літографій цього математичного об'єкту. Одна з відомих - показує мурах, що повзають по поверхні аркуша Мебіуса. Серію варіантів листа Мебіуса створив Макс Білл. Протягом майже 20 років він звертався до листа Мебіуса,  прагнучи висловити в скульптурі ідею вічного.

       Скульптура «Вузол без кінця» знаходиться в національному музеї сучасного мистецтва в Парижі.

     Стрічка Мебіуса надихнула багатьох митців на створення відомих скульптур, картин і для графічного мистецтва. Біля входу в Музей історії і техніки в Вашингтоні повільно обертається на п'єдесталі сталева стрічка, закручена на полвітка. У 1967 році в Бразилії відбувся міжнародний математичний конгрес. Його організатори випустили пам'ятну марку гідністю в п'ять сентаво. На ній була зображена стрічка Мёбіуса.І монумент заввишки більше ніж в два метри, і крихітна марка - своєрідні пам'ятники німецькому математику і астроному Август Фердинанд Мебіус, професору Лейпцігського університету.
  

Висновок

           Топологія знайшла своє застосування в алгебрі, геометрії, фізики, хімії, біології та в багатьох інших науках. Топологія розвивається і до цього дня. Кілька років тому петербурзький математик Григорій Перельман довів гіпотезу Пуанкаре, над якою билися на протязі ста років математики всього світу. За допомогою топології вчені навіть намагаються зрозуміти форму всесвіту і вивчати далекі туманності і чорні діри.

Отже, мої гіпотези підтвердилися:

Дійсно, топологія є частиною геометрії.

     Я дізнався, що про топології заговорили всього сто років тому. Це маленький вік для науки.

     Моя мета досягнена, завдання виконані.

     Я вважаю, що топологія буде дуже важлива в майбутньому для дослідження безкрайніх космічних просторів і для пошуку братів по розуму.

«Топологія, наймолодша і найпотужніша гілка геометрії, наочно демонструє плідну вплив протиріч між інтуїцією і логікою». Р. Курант