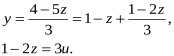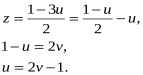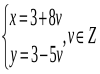Матеріал для факультативу "Діофантові рівняння"




Завданням шкільного курсу алгебри, є навчити учнів розв'язувати рівняння та задачі, що зводяться до них. Упродовж багатьох років алгебру розглядали як науку про рівняння і способи їх розв'язування. Велике значення рівнянь підкреслював А.Ейнштейн, він казав: «Мені доводиться ділити свій час між політикою і рівняннями. Проте рівняння, на мій погляд, набагато важливіші, тому що політика існує тільки для даного часу, а рівняння будуть існувати вічно».
Не можна стверджувати що, наприклад, тема «Функції» має меншу важливість, але навіть функцію, з певної точки зору, можна розглядати, як рівняння виду  , що виконується за певних умов та має певні властивості. Багато задач шкільного курсу геометрії теж розв'язується алгебраїчним способом, тобто за допомогою рівнянь.
, що виконується за певних умов та має певні властивості. Багато задач шкільного курсу геометрії теж розв'язується алгебраїчним способом, тобто за допомогою рівнянь.
Упродовж вивчення алгебри учні опановують уміння розв'язувати квадратні, ірраціональні, логарифмічні, тригонометричні, показникові рівняння, а також їх системи, але, усі ці рівняння відносяться до так званих визначених, тобто рівнянь з однією змінною або (якщо це система) систем, де кількість змінних дорівнює кількості рівнянь.
Існують рівняння, що мають кілька змінних або систем, де кількість змінних більша від кількості рівнянь. Задачі на подібні рівняння зустрічаються лише на математичних олімпіадах. Виникає питання: якщо учень не знайомий навіть з основами теорії невизначених рівнянь, як же він буде їх розв'язувати? Тому доцільно буде ознайомити учнів з найпростішими невизначеними, або діофантовими рівняннями .
До речі, не всі невизначені рівняння є діофантовими.
Діофантовими називаються лише ті алгебраїчні рівняння або їх системи з цілими коефіцієнтами, в яких кількість змінних більша, ніж кількість рівнянь, а знайти треба тільки цілі або раціональні розв'язки.
Діофантові рівняння дають велику можливість для розвитку логічного мислення учнів, бо загальних способів їх розв'язування немає, до кожного типу рівнянь треба підходити творчо, використовуючи пошукові методи.
Коли ж можна розпочати знайомство учнів з найпростішими діофантовими рівняннями? Невизначені рівняння все ж таки з'являються в шкільному курсі алгебри. У 7 класі вводять поняття лінійного рівняння з двома змінними або рівняння вигляду 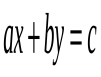 , вводять означення розв'язку подібного рівняння, а потім переходять до його геометричного змісту, але алгебраїчні способи розв'язування при цьому не розглядаються. Саме у цій темі можна почати розглядати основи теорії невизначених рівнянь першого степеня. Потім у 8 класі під час вивчення теми „Квадратні рівняння” показати способи розв’язування найпростіших діофантових рівнянь другого степеня і т. д. Більш ширше діофантові рівняння можна розглянути у ході підготовки до олімпіад, конкурсів.
, вводять означення розв'язку подібного рівняння, а потім переходять до його геометричного змісту, але алгебраїчні способи розв'язування при цьому не розглядаються. Саме у цій темі можна почати розглядати основи теорії невизначених рівнянь першого степеня. Потім у 8 класі під час вивчення теми „Квадратні рівняння” показати способи розв’язування найпростіших діофантових рівнянь другого степеня і т. д. Більш ширше діофантові рівняння можна розглянути у ході підготовки до олімпіад, конкурсів.

Про видатного математика античного світу – Діофанта Олександрійського,
 історія майже нічого не зберегла .В популярному в X-XIV ст. збірнику віршованих арифметичних задач „Грецька онтологія” вміщено задачу під назвою „Епітафія Діофанта”.
історія майже нічого не зберегла .В популярному в X-XIV ст. збірнику віршованих арифметичних задач „Грецька онтологія” вміщено задачу під назвою „Епітафія Діофанта”.
Задача зводиться до рівняння першого степеня, розв’язавши яке дізнаємося, що Діофант жив 84 роки. Ось і всі відомості про його життя.
Ще більшою загадкою, ніж біографія Діофанта, стала для науки його „Арифметика”, з 13 книг якої збереглося лише шість. У них подано 189 задач з розв’язаннями і поясненнями. За формою „Арифметика” просто збірник задач, але за змістом – унікальне явище, справжнє чудо історії математики.
Найпростіші діофантові рівняння розв’язували вже шумеро-вавілонські математики, піфагорійці й Евклід. Діофант розробляє, по суті, цілу теорію таких рівнянь. З неї в сучасній науці сформувалася окрема галузь математики – діофантовий аналіз, або діофантова геометрія.
Ідеям і задачам Діофанта судилася довга й щаслива доля. Він передав їх математикам Середньої Азії, Близького Сходу та Індії. У XVII ст. їх висвітлив по-новому П'єр Ферма (1601—1665). Відтоді проблеми, які заповів нащадкам Діофант, привертають увагу найвидатніших учених. Деякі з них розв'язані, інші — не розкрито й досі.
 П’єр Ферма (1601 - 1665), вивчаючи "Арифметику" Діофанта, зробив на полях цієї книги знамениту позначку: "Я знайшов воістину дивний доказ того, що рівняння
П’єр Ферма (1601 - 1665), вивчаючи "Арифметику" Діофанта, зробив на полях цієї книги знамениту позначку: "Я знайшов воістину дивний доказ того, що рівняння ![]() при n > 2, не має рішень у цілих числах, однак поля цієї книги занадто малі, щоб тут його умістити". Це одне із самих марних математичних тверджень, твердження одержало назву “Великої теореми Ферма" і, чомусь, викликало дійсний ажіотаж серед математиків і аматорів (особливо після того як У 1908 році німецький математик Пауль Вольфскель[en] заповів 100 тис. німецьких марок тому, хто доведе теорему Ферма). Однак після Першої світової війни премія знецінилася.
при n > 2, не має рішень у цілих числах, однак поля цієї книги занадто малі, щоб тут його умістити". Це одне із самих марних математичних тверджень, твердження одержало назву “Великої теореми Ферма" і, чомусь, викликало дійсний ажіотаж серед математиків і аматорів (особливо після того як У 1908 році німецький математик Пауль Вольфскель[en] заповів 100 тис. німецьких марок тому, хто доведе теорему Ферма). Однак після Першої світової війни премія знецінилася.
Німецький математик Герхард Фрай припустив, що Велика теорема Ферма є наслідком гіпотези Таніями - Сімура. Це припущення було доведено Кеном Рібет.
Про доведення теореми було оголошено влітку 1993 року. Під час триденної лекції в Інституті сера Ісаака Ньютона у Кембріджі
 Ендрю Вайлс озвучив основні принципи доведення гіпотези Таніями-Сімури, наслідком якої було доведення і Великої теореми Ферма. Але, коли рукописи з детальним доказом було передано на рецензування, в одному з розділів було знайдено суттєву помилку. Остаточне доведення теореми було здійснено Ендрю Вайлсом за участі Річарда Тейлора тільки 1995 року.[джерело?] 129-сторінкове доведення було надруковане у журналі «Annals of Mathematics[en]»[1].
Ендрю Вайлс озвучив основні принципи доведення гіпотези Таніями-Сімури, наслідком якої було доведення і Великої теореми Ферма. Але, коли рукописи з детальним доказом було передано на рецензування, в одному з розділів було знайдено суттєву помилку. Остаточне доведення теореми було здійснено Ендрю Вайлсом за участі Річарда Тейлора тільки 1995 року.[джерело?] 129-сторінкове доведення було надруковане у журналі «Annals of Mathematics[en]»[1].
У 2016 році за доведення Великої теореми Ферма Ендрю Вайлс отримав премію Абеля.
Отже,сама теорема була доведена в 1995 році; П’єр Ферма перебільшив на полях "Арифметики", тому що він фізично не міг придумати подібного доказу, що вимагає колосальної сукупності математичних знань. Елементарного доказу великої теореми Ферма поки ніхто з жителів нашої планети знайти не зміг, хоча над його пошуком билися кращі розуми .
 У 1900 р. видатний німецький математик
У 1900 р. видатний німецький математик
Д. Гільберт (1862—1943) на другому Міжнародному математичному конгресі виголосив доповідь «Математичні проблеми», в якій поставив перед вченими 23 задачі з різних розділів математики, розв'язання яких мало важливе значення для подальшого розвитку математики.
Десятою проблемою була «задача про розв'язність діофантового рівняння», сформульована так: «Нехай дано діофантове рівняння з довільними невідомими і цілими раціональними числовими коефіцієнтами. Назвіть спосіб, за допомогою якого можна після скінченого числа операцій встановити, чи розв'язне це рівняння в цілих раціональних числах».
Відповіді довелося чекати 70 років. У 1970 р. на Міжнародному математичному конгресі в Ніцці двадцятирічний радянський аспірант Юрій Володимирович Матіясевич сколихнув математичний світ справжньою сенсацією століття — доповів про розв'язання 10-ї проблеми Гільберта. Він довів, що ніякого загального методу для розв'язання діофантового рівняння не існує.
Доведення Матіясевича дало ще побічні результати, яких він не шукав і які буквально приголомшили математиків своєю несподіванкою. Виявилося, що існує цілочисловий многочлен (щоправда, досить високого степеня і від великого числа змінних) — такий, що при всіх цілих значеннях змінних, коли він додатний, він подає тільки прості числа. Виявляється, що універсальний генератор простих чисел, за яким полювали математики від Ейлера до наших днів, не казкова жар-птиця. Існує й такий многочлен, усі цілі значення якого (при цілих значеннях змінних) подають послідовність: ![]() , і тільки такі числа. Результати Матіясевича проливають світло на існування глибоких ще не ро згаданих залежностей на множині цілих чисел.
, і тільки такі числа. Результати Матіясевича проливають світло на існування глибоких ще не ро згаданих залежностей на множині цілих чисел.


Діофантовими називаються алгебраїчні рівняння і системи алгебраїчних рівнянь з цілими коефіцієнтами, що мають число невідомих, переважаюче число рівнянь. Система стає невизначеною і тому знаходять цілі або раціональні розв`язки.
Або Діофантовими рівняннями називаються рівняння виду 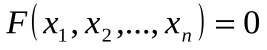
де Р(х,у,…z)-многочлен декількох змінних з цілими коефіцієнтами для яких потрібно знайти цілі розв’язки.

Розв’язати діофантове рівняння означає:
- З’ясувати ,чи має рівняння хоча б один ненульовий розв’язок в цілих числах;
- Якщо рівняння має розв’язок в цілих числах,то з’ясувати чи нескінченна множина його розв’язків;
- Знайти всі цілі розв’язки рівняння.
Лінійні діофантові рівняння виду ах+ву=с навчились розв’язувати ще
до Діофанта.
Стародавні греки знали, що якщо це рівняння має один цілий розв’язок(х0;у00 ,то його буде задовольняти нескінченна множина пар(х;у) виду х= х0+вк; у=у0-ак, де к –будь-яке ціле число.
Математики Стародавньої Греції та Стародавньої Індії знали методи розв’язання деяких рівнянь другого степеня виду ах2+вху+су2= dz2
Зокрема їм були відомі всі піфагорові трійки натуральних чисел х,у, z ,що задовольняють рівняння
х 2+у2=z2 Всі трійки взаємно простих піфагорійських чисел стародавні математики знаходили за формулами х=m2-n2, у=2mn, z =m2+n2 ,m,n-натуральні числа
Особливе місце серед діофантових рівнянь займає рівняння
х n+у n=zn, де n -натуральне число. Французький математик
П’єр Ферма довів,
що при n >2 рівняння х n+у n=zn не має розв’язків в натуральних числах x,y,z
Рівняння виду ![]() де
де ![]() -числа,а x,y-змінні,називають діофантовими рівняннями першого степеня з двома змінними.
-числа,а x,y-змінні,називають діофантовими рівняннями першого степеня з двома змінними.
Для розв’язання рівняння застосовують наступні теореми
Теорема 1. Якщо а і b –взаємно прості числа,то для будь-якого цілого
с ,рівняння ![]() має хоча б один розв’язок в цілих числах
має хоча б один розв’язок в цілих числах
![]()
![]() Теорема 2. Якщо а і b мають спільний натуральний дільник d = 1 ,а ціле число c не ділиться на d,то рівняння виду
Теорема 2. Якщо а і b мають спільний натуральний дільник d = 1 ,а ціле число c не ділиться на d,то рівняння виду![]() не має розв’язків в цілих числах.
не має розв’язків в цілих числах.
Теорема 3. Якщо а і b –взаємно прості числа,то Рівняння ![]() має
має
нескінченну кількість розв’язків, які знаходять за формулами
х= х0+вк; у=у0-ак, де (х0 ; у0 ) - будь-який цілий розв’язок
даного рівняння к – будь-яке ціле число.
Частинний розв'язок (х0 ; у0 ) можна знайти підбором, для малих а і b ,а у випадку коли числа а і b великі , то користуємось наступною теоремою
Теорема 4. НСД (а,в)= d може бути записаний у вигляді d= аm+bn, де m,n
цілі числа . d знаходимо за алгоритмом Евкліда.
Лінійним діофантовим рівнянням із двома невідомими називається рівняння виду ![]() де
де ![]() - цілі числа,
- цілі числа, ![]()
Це рівняння має безліч розв`язків: ,
,
де ![]() - будь-який розв`язок,
- будь-який розв`язок, ![]()
Метод спуску.
Для розв`язування діофантових рівнянь першого степеня з двома невідомими можна використовувати метод спуску.
Приклад 1. Розв`язати в цілих числах рівняння ![]()
Розв`язання
1.
Виберемо змінну, що має найменший коефіцієнт, і виразимо його через іншу змінну: ![]()
Виділимо цілу частину: ![]()
Все число буде цілим, якщо цілим виявиться значення ![]() Це можливо тоді, коли число
Це можливо тоді, коли число ![]() без остачі поділиться на 5. Вводимо нову змінну
без остачі поділиться на 5. Вводимо нову змінну ![]() , тоді останнє рівняння запишемо у вигляді:
, тоді останнє рівняння запишемо у вигляді: ![]() .
.
Ми прийшли до рівняння такого ж типу як і вихідне рівняння, але вже з меншими коефіцієнтами. Розв`язувати його потрібно відносно змінних ![]() і
і ![]() . Аналогічно:
. Аналогічно:
Дробів більше нема, спуск закінчено.
-
Тепер необхідно „піднятися нагору”. Виразимо через змінну спочатку
спочатку 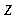 , потім
, потім  і
і 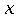 .
.
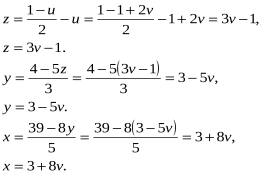
Формули становлять загальний розв’язок рівняння в цілих числах.
Відповідь: 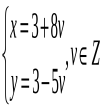
Приклад 2. Розв’язати в цілих числах рівняння ![]() методом спуску.
методом спуску.
Розв’язання
1
![]()
2
![]()
![]()
3![]()
4
![]()
![]()
5![]()
6![]()
![]()
7 ![]()
8 ![]()
9
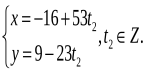
Відповідь:
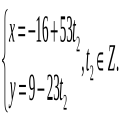
Приклад 3. Розв’язати в цілих числах рівняння ![]() методом спуску.
методом спуску.
Розв’язання:
1![]()
2![]()
![]()
![]()
3![]()
4 ![]()
![]()
5
![]()
6 ![]()
![]()
7
![]()
8 ![]()
9
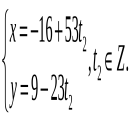
Відповідь: 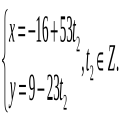
Приклад 3. Розв’язати в цілих числах рівняння ![]() методом спуску.
методом спуску.
Розв’язання: 12х=189-31у ;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
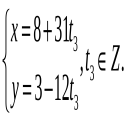
Відповідь:
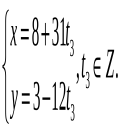
Використано ресурси інтернету
Матеріал підготувала:
Уварова Т.О.


про публікацію авторської розробки
Додати розробку