Пояснюючий матеріал до "Теорема Вієта"
Моя найулюбніша теорема
У багатьох людей є улюблені вірші, книги. У мене є улюблена теорема.
Це теорема Вієта для повних квадратних рівнянь, які мають раціональні корені. Уміння швидко знаходити корені квадратного рівняння має велике практичне значення не тільки в 8-9 класах, де учні тільки освоюють і закріплюють необхідні формули, але й у старших класах, де квадратні рівняння виникають як допоміжні при розв’язку значно більш складних завдань, при розв’язку тригонометричних, логарифмічних рівнянь і нерівностей. І тому особливо важливо, щоб учні максимально швидко справлялися з розв’язком цих рівнянь.
Відомо, що в більшості «шкільних» квадратних рівняннях, із цілими коренями, ці корені без особливих труднощів знаходять добором, заснованим на теоремі зворотній теоремі Вієта.
Я у своїй практиці вважаю досить важливим і необхідним рекомендувати учням саме таким способом розв’язувати рівняння. Якщо розв’язок квадратного рівняння за формулою вимагає в середньому 3-5хв., то це нестандартне розв’язання дозволяє знайти корені за 30-40 секунд. І це дозволяє розв’язувати більшу кількість вправ на уроках алгебри. Спираючись на свій досвід впевнена, що учня 10-11 класу , який має слабку базу по математиці, можна дуже швидко навчити розв’язувати повні квадратні рівняння, які мають раціональні корені, і при цьому дуже мала ймовірність одержання невірної відповіді.
Як я на уроках пропоную вивчати цю чудову теорему?
При вивченні теми “Квадратні рівняння” , згідно програми, спочатку відпрацьовую розв’язок неповних квадратних рівнянь; використовую теорему Вієта для розв’язку зведених квадратних рівнянь. Потім розв’язуємо повні квадратні рівняння по загальній формулі й по формулі з парним другим коефіцієнтом Учні порівнюють раціональність цих формул. Коли цей матеріал відпрацьований , я показую доведення теореми Вієта, для повного квадратного рівняння, що має раціональні корені й метод використання цього способу при розв’язуванні вправ.
Учні приходять у захват від простоти. В очах їх радість від отриманого відкриття. Цей урок для нас урок-свято. Проходить час і ця теорема стає улюбленою теоремою моїх учнів. Вони вільно нею володіють.
Деякі мої колеги теж користуються цією теоремою на уроках математики й вона допомагає їм розв’язувати складні завдання нашого предмета.
Математика-наука точна, вимагає точних доведень, науковості.
Приведу доказ теореми Вієта для розв’язку квадратних рівнянь , що мають раціональні корені.(див. посібник для вчителя. О.Г. Гайштук, Г.М. Литвинченко. «Розв’язування алгебраїчних задач», 1990).
Нехай дане повне квадратне рівняння: ax2+bx+c=0 (1) яке має раціональні корені х1 і х2.
Помноживши обидві частини рівняння на а,, одержимо
а2 х2+abx+ac=0
Позначимо ах=у, одержимо рівняння: у2 + by + ac=0 (2)
Це рівняння відрізняється від даного (1) тим, що перший коефіцієнт рівний 1, а останній – добутку крайніх коефіцієнтів. Рівняння (2)
стало зведеним і таким, що має цілі корені. Їх легко знайти усно, використовуючи теорему Вієта.
Нехай це будуть значення у1 і у2 . Тоді вертаючись до підстановки , знайдемо:
ах=у1; ах=у2
Маємо х1== у1 /а , ; х2= у2/а
Висновок: щоб повне квадратне рівняння, яке має дробові корені, розв’язати усно, використовуючи теорему Вієта, треба:
- Звести дане рівняння ax2+bx+c=0, до рівняння виду: у2+by+ac=0.
- Кожний отриманий після розв’язку зведеного квадратного рівняння корінь поділити на перший коефіцієнт повного квадратного рівняння.
Приклад: розв’язати усно рівняння.
2х2- 9х+10=0
-9х+20=0
х1=4/2=2
х2=5/2=2,5
Відповідь: 2;2,5
Приклади на використання теореми Вієта.
- 5х2 -3х -2=0
- 16х2-6х-1=0
- 3х2-8х+4=0
- 3х2 +5х-8=0
- 3х2 -х-4=0
- 5х2 -3х-8=0
- 4х2+3х-7=0
У класах з поглибленим вивченням математики можна запропонувати для усного знаходження коренів наступні рівняння:
-
х2-7ax+12
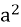 =0
=0
-
х2-5bx+6
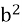 =0
=0
-
7 х2-4ax+3
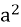 =0
=0
-
7 х2+13bx+6
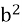 =0
=0
-
х2-(
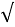 2+1)x+
2+1)x+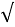 2 =0
2 =0
-
х2+(
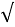 3 -2)x-2
3 -2)x-2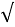 3 =0
3 =0
-
х2+(
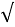 2 +
2 +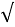 6)+2
6)+2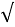 2 =0
2 =0
-
х2-(
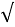 5 +
5 +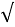 15)x +5
15)x +5 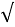 3 =0
3 =0
Бажаю успіхів


про публікацію авторської розробки
Додати розробку
