Матеріал для підготовки до ДПА, ЗНО з теми "Трапеція"
Матеріал для підготовки до ДПА, ЗНО з теми "Трапеція". Розробка містить теоретичний матеріал, 17 розв'язаних задач різного рівня складності з поясненням. Розрахована для вчителів та учнів 8-11 кл.
Матеріал для підготовки до ДПА, ЗНО Тема. Трапеція.
|
|
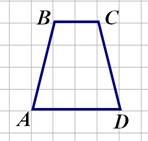
Чотирикутник, у якого дві сторони паралельні, а дві інші сторони непаралельні, називається трапецією
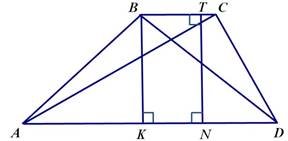
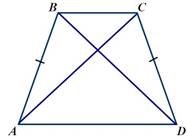
ABCD – трапеція, AD || BC- основи, AB і CD – бічні сторони, AC і BD – діагоналі, BK і TN – висоти. |
|
|
ОКРЕМІ ВИДИ ТРАПЕЦІЇ |
||
|
|
Рівнобічна трапеція – трапеція з рівними бічними сторонами (АВ = CD) Властивості: Кути при основі рівні: ВАС CDA , CВА BCD Діагоналі рівні: АС = ВD
|
|
|
|
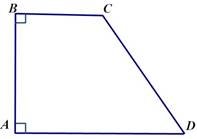
Прямокутна трапеція – це трапеція, у якої одна бічна сторона перпендикулярна до основ
hпрямокутної трапеції = AB
|
|
|
СЕРЕДНЯ ЛІНІЯ ТРАПЕЦІЇ
|
||
|
|
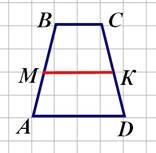
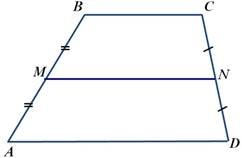
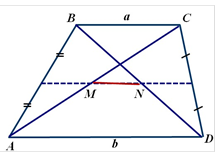
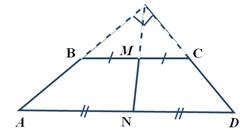
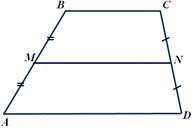
Відрізок, який сполучає середини бічних сторін трапеції, називається середньою лінією трапеції МN – середня лінія Властивості: МN || AD, МN || BC Середня лінія трапеції паралельна основам і дорівнює їх півсумі AD BC MN 2
|
|
|
|
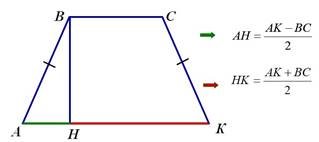
Висота трапеції, проведена з вершини тупого кута, поділяє основу трапеції на два відрізки, менший з яких дорівнює піврізниці основ, а більший – півсумі основ
|
|
|
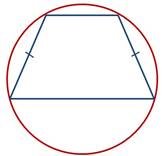
Якщо трапецію можна вписати в коло, то трапеція – рівнобічна.
Навколо рівнобічної трапеції можна описати коло.
|
|
|
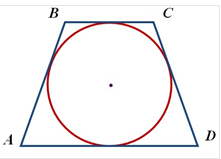
В трапецію можна вписати коло, якщо сума основ трапеції дорівнює сумі її бічних сторін
AB + CD = BC + AD
|
|
|
Якщо в рівнобічній трапеції діагоналі перпендикулярні, то висота дорівнює півсумі основ.
a b h 2
|
|
|
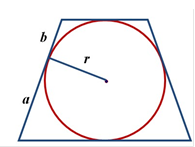
Якщо в трапецію вписане коло з радіусом r і вона ділить бічну сторону точкою дотику на два відрізка – a і b,
|
|
|
Відрізок, який з’єднує середини діагоналей, дорівнює піврізниці основ і лежить на середній лінії
b a MN 2
|
|
|
|
Центр вписаного кола є точкою перетину бісектрис кутів трапеції.
Кут, утворений бісектрисами кутів, прилеглих до бічної сторони трапеції прямий (COD900 ). |
|
|
|
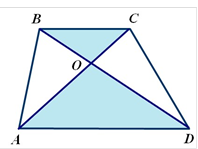
Трикутники AOD іCOB , утворені відрізками діагоналей і основами трапецій, подібні. ABO~ COB AD Коефіцієнт
подібності – k
Відношення площ цих трикутників –k2 |
|
|
|
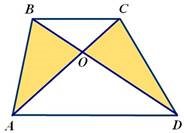
Трикутники ABOі DCO , утворені відрізками діагоналей і бічними сторонами трапеції, мають однакову площу.
|
|
|
|
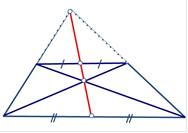
Точка перетину діагоналей трапеції, точка перетину продовження її бічних сторін і середини лежать на одній прямій.
|
|
|
|
Якщо сума кутів при будь-якій основі трапеції дорівнює 900, то відрізок, що з’єднує середини основ, дорівнює їх піврізниці. AD BC MN 2
|
|
|
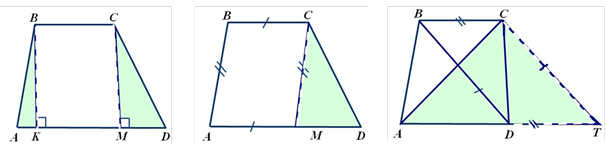
ДОДАТКОВА ПОБУДОВА ДЛЯ ТРАПЕЦІЇ |
||
|
|
||
|
BK AD, CM AD СМ || ВА СТ || BD |
||
|
ПЛОЩА, ПЕРИМЕТР ТРАПЕЦІЇ |
||
|
|
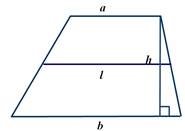
a b S 2
S l h, l – середня лінія
P a b c d
|
|
|
|
MN - cередня лінія трапеції BC AD MN= 2
|
|
Задача №1.
Як можна закінчити речення «У будь-якій трапеції…», щоб утворилося правильне твердження?
А) діагоналі точкою перетину діляться навпіл;
Б) діагоналі рівні;
В) дві сторони рівні;
Г) дві сторони паралельні. Відповідь: Г).
Задача №2.
Кути трапеції ABCD, прилеглі до основи ВС, дорівнюють 700 і 1600. Знайдіть кути, прилеглі до основи AD.
|
А) 200,1100 |
Б) 400, 1300 |
В) 500 і 1200 |
Г) такої трапеції не існує |
Розв’язання:
Нехай В 700і С 1600. Тоді АіВ прилеглі до бічної сторони АВ є внутрішніми односторонніми кутами при паралельних прямих BC і AD та січній АВ. Тоді А=1800 -В=1800 -700 = 1100. Аналогічно D =1800 - С = 1800 - 1600 = 200.
Відповідь: А.
Задача №3.
Одна з основ трапеції дорівнює 14см, а її середня лінія – 8см. Знайдіть другу основу трапеції.
|
А) 22 см |
Б) 11 см |
В) 4 см |
Г) 2 см |
Розв’язання:
14 х
![]()
8; 14 х 16; х
2(см);
8; 14 х 16; х
2(см);
2
Відповідь: Г).
Задача №4.
Основи трапеції відносяться як 3:7, а її середня лінія дорівнює 40см. Знайдіть основи трапеції.
|
А) 12 см, 28 см |
Б) 24 см, 56 см |
В) 48 см, 112 см |
Г) 18 см, 42 см |
Розв’язання:
3х 7х
![]()
40; 10х
80; х
8;
40; 10х
80; х
8;
2
3х 38 24; 7х 78 56. Відповідь: Б)
Задача №5.
Гострий кут прямокутної трапеції в 3 рази менший від тупого кута. Знайдіть ці кути.
|
А) 450 і 1350 |
Б) 600 і 1200 |
В) 100 і 300 |
Г) 300 і 600 |
|
Розв’язання: 3х + х =180; 4х =180; х = 450 3х 345 135. Відповідь: А).
Задача №6. Основи трапеції відносяться як 2 : Знайдіть основи трапеції. |
|
орівнює 28см. |
|
|
А) 8 см, 20 см |
Б) 16 см, 40 см |
В) 32 см, 80 см |
Г) 12 см, 30 см |
Розв’язання:
2х 5х
![]()
28; 7х
56; х
8;
28; 7х
56; х
8;
2
2х 28 16; 5х 58 40.
Відповідь: Б).
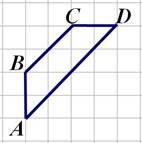
 Задача
№7.
Задача
№7.
Знайдіть середню лінію трапеції АВСD, якщо сторони квадратних кліток дорівнює 1.
Розв’язання:
Середня лінія трапеції дорівнює півсумі її основ.
![]() MK
AD
BC
4
2
3.
MK
AD
BC
4
2
3.
2 2
Відповідь: 3.
Задача №8.
![]()
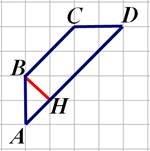 Знайдіть
висоту трапеції АВСD, опущену
із вершини В, якщо сторони квадратних кліток дорівнюють 2 .
Знайдіть
висоту трапеції АВСD, опущену
із вершини В, якщо сторони квадратних кліток дорівнюють 2 .
Розв’язання: За теоремою Піфагора
![]() ВН2
= ( 2 )2+(
2 )2 = 2+2 =
4
ВН2
= ( 2 )2+(
2 )2 = 2+2 =
4
ВН = 2
Відповідь: 2.

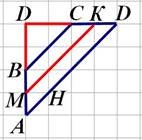 Задача
№9.
Задача
№9.
![]() Знайдіть середню лінію трапеції АВСD,
якщо сторони квадратних кліток дорівнюють 2 .
Знайдіть середню лінію трапеції АВСD,
якщо сторони квадратних кліток дорівнюють 2 .
Розв’язання:
За теоремою Піфагора:
 AD (4 2)2 (4 2)2 64 8,
AD (4 2)2 (4 2)2 64 8,
BC (2 2)2 2 2)2 16 4.
![]() MK AD BC
8
4
6.
MK AD BC
8
4
6.
2 2
Відповідь: 6.
Задача №10.
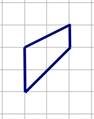 Знайдіть площу трапеції,
зображеної на папері в клітинку з розміром клітки 1 см х 1 см.
Відповідь дайте у квадратних
Знайдіть площу трапеції,
зображеної на папері в клітинку з розміром клітки 1 см х 1 см.
Відповідь дайте у квадратних
сантиметрах.
Розв’язання:
S
![]() 2 3 (см2 ).
2 3 (см2 ).
Відповідь: 3 см2.
Задача №11.
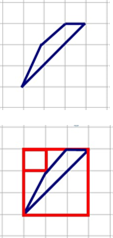 Знайдіть
площу трапеції, зображену на папері в клітку з розміром клітки 1 см х 1 см.
Відповідь дайте у квадратних сантиметрах. Розв’язання:
Знайдіть
площу трапеції, зображену на папері в клітку з розміром клітки 1 см х 1 см.
Відповідь дайте у квадратних сантиметрах. Розв’язання:
Площа трапеції дорівнює різниці площі більшого квадрата, маленького квадрата і трьох прямокутних трикутників, гіпотенузи яких є сторонами даного чотирикутника. Тому
S 3311 ![]() 33
33 ![]() 12
12 ![]() 11 2(см2 ).
11 2(см2 ).
Відповідь: 2 см2.
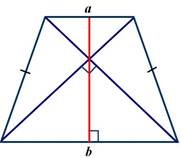
Задача №12. (Про властивість висоти, проведеної з вершини тупого кута у рівнобічній трапеції.)
![]() Довести, що висота,
проведена з вершини тупого кута рівнобічної трапеції з основами а і b,
розбиває більшу основу на частини, які дорівнюють a b a b і .
Довести, що висота,
проведена з вершини тупого кута рівнобічної трапеції з основами а і b,
розбиває більшу основу на частини, які дорівнюють a b a b і .
2 2
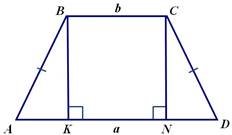 Дано:
Дано:
ABCD – трапеція, де AB =CD, AD = а, BC = b, ВКАD Довести:
AB ![]() a b ; KD
a b ; KD ![]() a b
a b
2 2
Доведення.
В трапеції ABCD проведемо СNАD. BAK CDN як кути при основі рівнобічної трапеції, АВ = CD за умовою, тому ABK DCN за гіпотенузою і гострим кутом, звідки AK = ND як відповідні сторони рівних трикутників.
KN = BC = b, оскільки KCBN – прямокутник. a b
Маємо
AK AD KN( ):2 або AК ![]() .
.
2
a b 2a a b a b
![]() Виразимо КD AD AK a ,
що і треба було
Виразимо КD AD AK a ,
що і треба було
2 2 2
довести.
Задача №13.
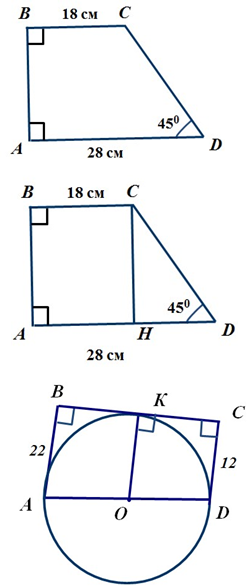
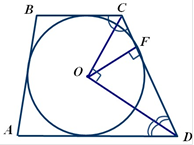
Відстані від центра кола, вписаного у прямокутну трапецію, до кінців більшої бічної сторони дорівнюють 12 см і 16 см. Знайдіть площу круга, який обмежений цим колом.
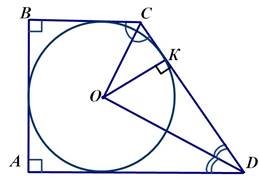 Дано:
Дано:
АВСD – прямокутна трапеція
А В 900
СО = 12 см, DО =16 см (ООК; )- вписане в трапецію Знайти:
Sкруга
Розв’язання:
На рисунку точка О є точкою перетину бісектрис кутів ВСD і СDА. У OCD :
 СOD 1800 ( OCDOCD) 1800 (BCD ADC) 1800
СOD 1800 ( OCDOCD) 1800 (BCD ADC) 1800
2 2
![]() BCDADC 1800 1800) 900. Отже, OCD - прямокутний, ОС
і ОD -
BCDADC 1800 1800) 900. Отже, OCD - прямокутний, ОС
і ОD -
2 2
 його катети. Тоді CD OC OD
2 2
12 16 202
2 (cм). Нехай К – точка
дотику вписаного кола до сторони CD. Оскільки OKCD,
то OK – висота
його катети. Тоді CD OC OD
2 2
12 16 202
2 (cм). Нехай К – точка
дотику вписаного кола до сторони CD. Оскільки OKCD,
то OK – висота
прямокутного трикутника OCD. Виразимо площу S цього трикутника двома
1 1 2 2
способами: S ![]() OC OD
OC OD ![]() CD OK .
Звідси маємо OCOD CDOK ,
CD OK .
Звідси маємо OCOD CDOK ,
OK ![]() OC OD ,
OK
12 16
OC OD ,
OK
12 16![]()
9,6(см), ОК = r –
радіус кола.
9,6(см), ОК = r –
радіус кола.
CD 20
![]() Тоді площа круга, який обмежений
цим колом, Sкр = ∙ r2 = ∙ 9,62 = 92,16
Тоді площа круга, який обмежений
цим колом, Sкр = ∙ r2 = ∙ 9,62 = 92,16 ![]() (см2).
(см2).
Відповідь: 92,16![]() см2.
см2.
Задача №14.
Дано:
ABCD- трапеція SМСК = SABСМ
АК = а, ВС=b Знайти: МК Розв’язок:
На рисунку зображено трапецію ABCD. Нехай АК = а, ВС=b. Проведемо висоту трапеції – CF= h.
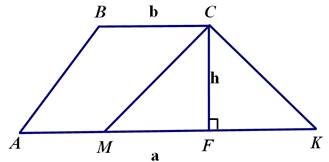 SМСК =
SМСК = ![]() МК h
МК h
1
SABCM ![]() (BC AM h ) 2
(BC AM h ) 2
![]() МК h
=
МК h
=![]() (BC
AM)h
(BC
AM)h
МК= ВС+АМ = b +АМ МК= АК-АМ = а - АМ b +АМ = а - АМ а b
АМ = ![]()
2
а b а b
![]() МК
= a - =
МК
= a - =
2 2
а b
Відповідь: МК
= ![]()
2
Задача №15.
![]()
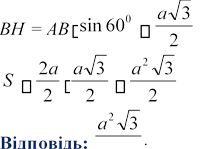 Бічна сторона
рівнобічної трапеції, описаної навколо кола, дорівнює а, а один із кутів
– 60[1].
Знайдіть площу трапеції.
Бічна сторона
рівнобічної трапеції, описаної навколо кола, дорівнює а, а один із кутів
– 60[1].
Знайдіть площу трапеції.
Дано:
ABCD - рівнобічна трапеція, описана навколо кола
AB = CD = а
ВАD 600
Знайти: Sтр.
Розв’язання:
AD BC
Проведемо
висоту ВH. S = ![]() BH . Якщо трапеція описана
навколо 2
BH . Якщо трапеція описана
навколо 2
кола, то
 Задача №16.
Задача №16.
Знайдіть площу трапеції, зображену на рисунку.
Розв’язання:
Проведемо CHAD.
Розглянемо СHР, H 900 ,
HCD 900 D=900 - 450 = 450.
Тому, СHР- рівнобедрений з основою СD. CH=28 - 18=10 (cм); CH = HD= 10(см)
Sтр. ![]() AD BC CH
AD BC CH ![]() 2818 10 230(см2 )
2818 10 230(см2 )
2 2
Відповідь: 230 см2.
Задача №17 .
Кінці діаметра кола віддалені від дотичної до цього кола на 12 см і 22 см. Знайдіть діаметр кола. Розв’язання:
BC - дотична, AB і CD – перпендикуляри до BC. Якщо АВВС і СDВС. АВСD – прямокутна
трапеція. КО – середня лінія трапеції, радіус кола. КО = (12+22) : 2 = 17 (см). Діаметр: 2КО = 2·17=34
(см)
Відповідь: 34 см.
Використана література
1. Геометрія : підруч. для 8 кл. загальноосвіт. навч. закл./ О.С. Істер.- Київ : Генеза, 2016. – 216 с.
2. Геометрія : підруч. для 8 кл. загальноосвіт. навч. закл./ А.Г. Мерзляк, В. Полонський, М.С. Якір. - Х : Гімназія, 2016. – 208 с. : іл.
3. Збірники завдань для проведення ДПА в 9 класі з математики 2013-2017 років.


про публікацію авторської розробки
Додати розробку

-

Шевченко Катерина Сергіївна
31.01.2024 в 03:16
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Колесников Сергій Олексійович
03.02.2022 в 08:49
Дякую за роботу !
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Ціхановська Леся
19.01.2021 в 23:41
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Майданник Віта Святославівна
28.06.2019 в 12:35
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Ямнюк Наталія Олексіївна
18.03.2018 в 21:15
Дібрані цікаві задачі різного рівня складності.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

T Y
18.03.2018 в 15:20
Дуже потрібні дані для підготовки до ЗНО та ДПА, всім рекомендую!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 3 відгука