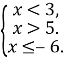матеріал до уроку"Показникові нерівності із змінною основою"
Показникові нерівності зі змінною основою
Узагальнений метод інтервалів має перевагу перед традиційним методом розв'язування показникових нерівностей зі змінною основою. Але визначити знаки даних функцій на проміжках не завжди легко. Тому під час розв'язування означених нерівностей, використаємо метод рівнозначних замін.
Показникові нерівності зі змінною основою
Узагальнений метод інтервалів має перевагу перед традиційним методом розв’язування показникових нерівностей зі змінною основою. Але визначити знаки даних функцій на проміжках не завжди легко. Тому під час розв’язування означених нерівностей використаємо метод рівнозначних замін.
Твердження 1. Вирази ![]() та
та ![]()
Доведення. Нехай ![]() , тобто
, тобто ![]() . Якщо
. Якщо ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Алгоритм розв’язування показникової нерівності методом рівнозначних замін![]() ):
):
- Знаходимо ОДЗ нерівності.
-
Переходимо до нерівності
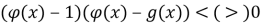 .
.
Отримали раціональну нерівність, яку розв’язуємо методом інтервалів
Відомо, що розв’язування нерівності виду ![]() на множині, де
на множині, де ![]()
![]()
1)![]() 2)
2)![]() 3)
3)![]()
Такі нерівності розв’язуються лише за умови, коли ![]()
![]() при
при ![]()
![]() при
при ![]()
Означення 1. Степенем числа ![]()
![]()
![]()
![]()
Означення 2. ![]() , де
, де ![]()
![]()
![]()
![]()
![]()
![]()
![]() для
для ![]()
Означення 3. ![]() , якщо
, якщо ![]()
![]()
![]() , де
, де![]()
Означення 4. ![]() , якщо
, якщо ![]()
![]()
Отже, якщо основа степеня – число від’ємне, то показником степеня може бути лише ціле число; якщо основа степеня дорівнює нулю, то показник степеня може бути натуральним або додатним дробовим числом, тобто додатним раціональним числом.
Розв’язування нерівності виду ![]() на множині, де
на множині, де ![]()
![]()
![]()
1)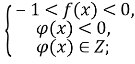 2)
2)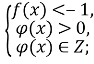 3)
3)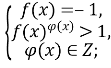 4)
4)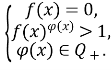
Приклад . Розв’язати нерівність ![]()
Розв’язання. Розглянемо дану нерівність на множині R. маємо, що
![]()
Отже, ![]()
Якщо ![]()
![]() задовольняє нерівність.
задовольняє нерівність.
Відповідь. ![]()
Приклад . Розв’язати нерівність ![]() .
.
Розв’язання. Розглянемо сукупність усіх семи систем, щоб показати, до чого може привести об’єднання деяких систем:
![]()
![]()
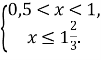
![]()
![]()
2.![]()
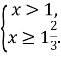
![]() Отже,
Отже, ![]()
![]()
![]()
![]()
4.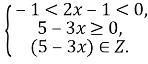
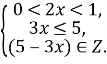
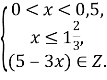
![]()
Знайдемо ті значення ![]()
![]() і які належать проміжку
і які належать проміжку ![]() . Нехай
. Нехай ![]() , де
, де ![]()
![]() . Підставимо це значення
. Підставимо це значення ![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]() .
.
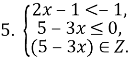
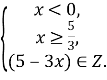
![]()
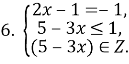
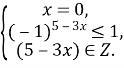
![]()
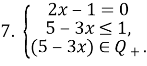
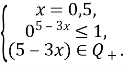
![]()
Відповідь. ![]()
![]() .
.


про публікацію авторської розробки
Додати розробку