Матеріал до уроку "Задача на побудову рівнобедреного прямокутного трикутника"
Сахненко А.І., учитель математики
Білоцерківської ЗОШ І-ІІІ ступенів №3 ім. Т.Г. Шевченка
Білоцерківської міської ради
Київської області
Пропоную свою задачу, яку можна розв’язувати з учнями при підготовці їх до олімпіад, а також розв’язувати на факультативних заняттях.
Задача. Маємо дві прямі, які перетинаються і точку, яка не лежить на них. Побудувати рівнобедрений прямокутний трикутник (рівносторонній трикутник) з вершиною в цій точці, якщо дві інші його вершини лежать на даних прямих.
 Розв’язання. Нехай маємо прямі a і b, які перетинаються в точці O і точку M, яка належить (наприклад) гострому куту
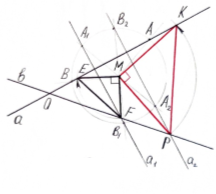
Розв’язання. Нехай маємо прямі a і b, які перетинаються в точці O і точку M, яка належить (наприклад) гострому куту ![]() (див. Рис.1)
(див. Рис.1)
![]() Виконаємо поворот прямої a на кут 90° проти годинникової стрілки. Для цього на прямій a візьмемо дві довільні точки А і В. При цьому повороті вони перейдуть у відповідні точки А1 і В1. Пряма А1В1 (пряма a1) перетне пряму b у точці F. При повороті точки F на кут 90° за стрілкою годинника вона перейде у точку E, яка буде належати прямій a.
Виконаємо поворот прямої a на кут 90° проти годинникової стрілки. Для цього на прямій a візьмемо дві довільні точки А і В. При цьому повороті вони перейдуть у відповідні точки А1 і В1. Пряма А1В1 (пряма a1) перетне пряму b у точці F. При повороті точки F на кут 90° за стрілкою годинника вона перейде у точку E, яка буде належати прямій a. ![]() – рівнобедрений і прямокутний.
– рівнобедрений і прямокутний.
Якщо пряму а повертати на кут 90° за стрілкою годинника, то вона перейде в пряму А2В2 (пряму а2), яка перетне пряму b у точці Р. Виконавши поворот точки Р на кут 90° проти годинникової стрілки ми одержимо точку К, яка буде лежати на прямій a. ![]() – прямокутний і рівнобедрений.
– прямокутний і рівнобедрений.
Задача має два розв’язки.
 Якщо точка M належить тупому
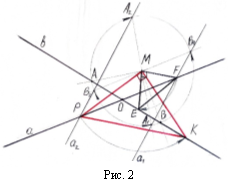
Якщо точка M належить тупому ![]() , то виконавши аналогічні побудови одержимо два рівнобедрених трикутники (див. Рис.2)
, то виконавши аналогічні побудови одержимо два рівнобедрених трикутники (див. Рис.2)
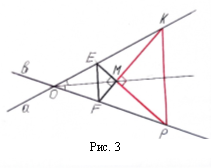
Якщо точка M буде лежати на бісектрисі цих кутів, то трикутники будуть розміщуватись так, як показано на рис.3 та рис.4. Тут поворот можна і не використовувати. Досить побудувати ![]() . І в цих випадках задача буде мати два розв’язки.
. І в цих випадках задача буде мати два розв’язки.

 Якщо
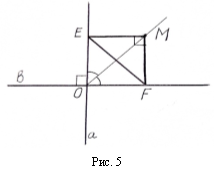
Якщо ![]() і точка M лежить на бісектрисі кута, то задача має один розв’язок (див. Рис.5). Якщо точка M не лежить на бісектрисі, то побудову треба виконувати точно так само, як описано на початку.
і точка M лежить на бісектрисі кута, то задача має один розв’язок (див. Рис.5). Якщо точка M не лежить на бісектрисі, то побудову треба виконувати точно так само, як описано на початку.
Виконайте самостійно таку побудову і ви побачите несподівані результати при певних положенням точки M.
Якщо трикутник рівносторонній, то повороти треба виконувати на + 60° і - 60°.


про публікацію авторської розробки
Додати розробку
