Урок геометрії "Розв'язування трикутників"
Урок геометрії 8 клас
Тема. Розв’язування прямокутних трикутників.
Мета. Закріпити знання учнів про співвідношення між сторонами і кутами прямокутного трикутника. Продовжити роботу над формуванням навичок знаходження невідомих елементів трикутників. Формувати навички практичного застосування набутих знань. Сприяти розвитку логічного та критичного мислення. Виховувати прагнення до знань, інтерес до математики та її історії.
Девіз уроку. Світ, що нас оточує – це світ геометрії. Пізнаваймо його!
Хід уроку
- Організаційний момент.
- Перевірка домашнього завдання. Відповісти на запитання, що виникли у учнів в процесі виконання домашнього завдання, в кінці уроку зібрати зошити.
-
Актуалізація опорних знань.
- Повторення теоретичного матеріалу з допомогою гри «Математичне лото». На дошці прикріплені картки, розділені на дві частини, на кожній з яких початок або кінець твердження. Команди по черзі складають ланцюжок тверджень. Якщо неправильно, то команда пропускає хід. Виграє та команда, яка швидше складає ланцюжок. Також у грі можлива нічия. (картки - Додаток 1).
- Повторення співвідношень між сторонами і кутами прямокутного трикутника. Робота з картками. Кожна картка розділена на три частини. Учитель показує тільки першу частину з питанням, потім поступово розгортає картку після відповідей учнів. (Додаток 2).
- Мотивація навчання. Ознайомлення з відомостями з історії математики.
Вчитель. Діти, цікаво, а чи давно виникла потреба уміти обчислювати синуси, косинуси, тангенси гострих кутів. Виявляється існує ціла наука, що вивчає ці співвідношення – тригонометрія. Що таке тригонометрія? Про це розкаже нам …
Виступ учениці. Тригонометрія - наука про вимірювання трикутників.
Ви знаєте, що стародавні мандрівники орієнтувалися за зорями та планетами. Вони могли досить точно визначити місцезнаходження корабля в океані або каравану в пустелі за розташуванням світил на небосхилі. При цьому одним з орієнтирів була висота, на яку піднімалося над горизонтом те або інше небесне світило в даній місцевості в певний момент часу. Зрозуміло, що безпосередньо виміряти цю висоту неможливо. Тому вчені стали розробляти методи непрямих вимірювань. Тут істотну роль відігравало розв’язування трикутника, дві вершини якого лежали на поверхні Землі, а третя була зорею.
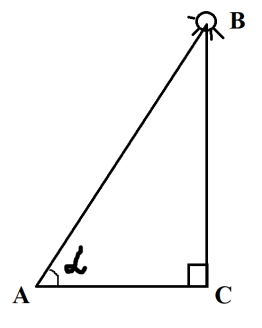
Для розв’язування подібних задач стародавнім астрономам потрібно було навчитися знаходити взаємозв’язки між елементами трикутника. Так виникла тригонометрія — наука, яка вивчає залежність між сторонами та кутами трикутника. Термін «тригонометрія» (від грецьких слів «тригонон» — трикутник і «метрео» — вимірювати) означає «вимірювання трикутників». В даному випадку вимірювання трикутників слід розуміти як розв'язування трикутників, тобто визначення сторін, кутів та інших елементів трикутника, якщо дано деякі з них.
Поняття синуса й косинуса з’являються в тригонометричних трактатах індійських учених у IV—V ст. н. е. У Х ст. арабські вчені оперували поняттям тангенса, яке виникло з потреб гномоніки — учення про сонячний годинник. Відношення катета, протилежного куту ![]() , до прилеглого катета вони називали словом «тінь». Пізніше, в XVI ст. , це відношення дістало назву «тангенса».
, до прилеглого катета вони називали словом «тінь». Пізніше, в XVI ст. , це відношення дістало назву «тангенса».
Вчитель. Так древні астрономи і землеміри застосовували тригонометрію для своїх потреб. І в наш час велика кількість практичних задач планіметрії, стереометрії, астрономії, геодезії та інших наук зводяться до задачі розв'язування трикутника.
-
Розв’язування задач.
- За 800 метрів від місця підйому літака прямо по курсу видно дерева, висота яких 14 метрів. Під яким кутом має злетіти літак, щоб не зачепити верхівки дерев?

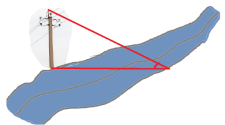
- Телеграфний стовп висотою 14 метрів знаходиться на березі річки. Верхній кінець стовпа видно з іншого берега під кутом 22о до горизонталі. Треба знайти ширину річки.
- Дорожній знак «крутий спуск» попереджає водіїв про небезпеку і вказує на скільки метрів у середньому піднімається дорога на кожні 100 м шляху. Знайдіть кут нахилу дороги, про який попереджає знак.

- Переріз залізничного насипу має форму рівнобічної трапеції, основи якої дорівнюють 8 м і 28 м. Бічні сторони нахилені до горизонту під кутом 31о. Знайдіть висоту насипу.
- Ширина будинку 7 м, довжина крокви – 4,5 м. під яким кутом крокви нахилені до стелі?
-
Підбиття підсумків уроку.
- Що ви дізналися нового на уроці?
- Де застосовуються задачі на розв’язування трикутників? ( складання кластера)
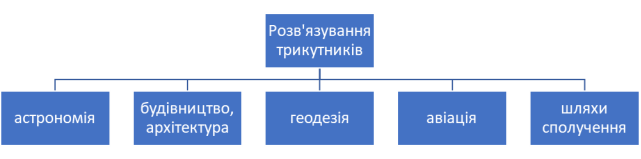
Вчитель. Якби урок тривав довше ніж 45 хвилин, ми змогли б розв’язати ще більше таких задач і доповнити кластер іншими галузями застосування трикутників.
- Поставте своєму настрою та роботі на уроці «лайк» або «дизлайк».
-
Домашнє завдання.
- Вертикальний промінь прожектора перетинає хмару. Яка висота нижньої межі хмари, якщо спостерігач, який стоїть на відстані 600 м від прожектора, бачить місце перетину прожектора і хмари під кутом 75о?
- Санаторій розташований на вершині гори. Пряма дорога до санаторію довжиною 1500 м має кут підйому 5о. На якій висоті від підошви гори розташований санаторій?
Додаток 1.
«Математичне доміно»
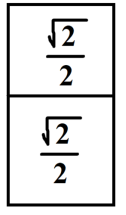





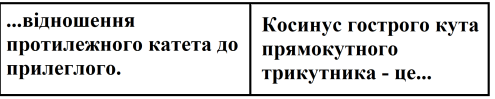
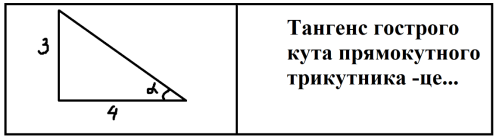

Додаток 2.


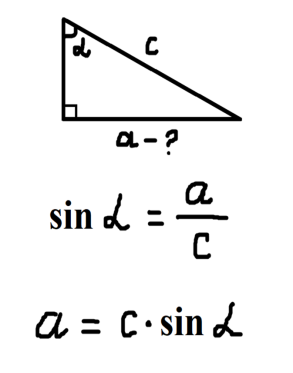
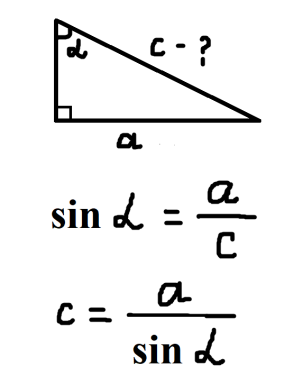
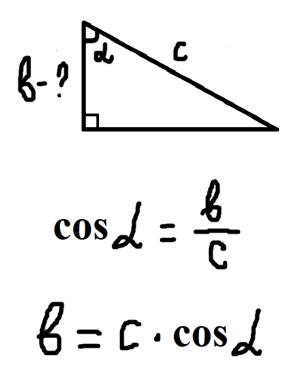


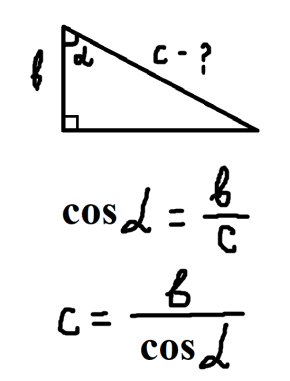
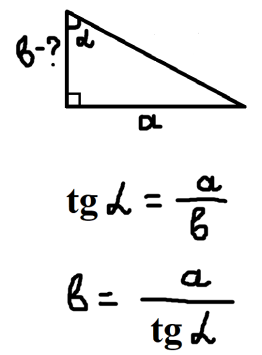


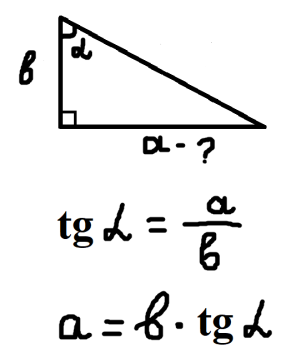


про публікацію авторської розробки
Додати розробку
