Матеріали для математичного гуртка з теми "Діаграми Ейлера-Венна"

ДІАГРАМИ ЕЙЛЕРА-ВЕННА

  Для  наочного  зображення  множини  елементів  довільної  природи  представляють  у  вигляді  множин  точок, обмежених  кривими, що  не  мають  самоперетинів. Такі  зображення  називають  діаграмами  Ейлера – Венна. За допомогою  таких  діаграм  зручно  зображати  відношення  між  множинами. Наприклад, якщо  ми  хочемо  наочно  зобразити, що множина  А  є  власною  підмножиною  множини  В ( А ʗ В ), то  зображаємо  ці  множини  так, як  показано  на  малюнку 1.

                                                                                                Мал. 1

Звичайно, всі  множини, якими  оперують  у  тому  або  іншому  випадку, є підмножинами  деякої  фіксованої  множини  U, яку  називають  універсальною. Універсальну  множину   U  часто  наочно  зображають  у  вигляді  прямокутника. Проілюструємо  з  допомогою  діаграм  Ейлера – Венна  операції  об’єднання  та  перерізу  двох  множин. Об’єднання  двох  множин  А і В  складається  з  тих  і  тільки  тих  елементів, які належать  принаймні  до  однієї  з  множин  А або  В  ( або А, або  В, або обом  множинам). Якщо  деякі  елементи  входять  у  множину  А  і  в  множину  В, то  в   об’єднання  ці  елементи  входять  лише  один  раз. Отже, для  скінчених  множин  А і  В  кількість  елементів   об’єднання  А і  В   множин  може  бути  меншою,  ніж  сума  кількості  елементів  множин   А  і   В. Нехай  множини  А і В зображено  з  допомогою  двох  діаграм. Тоді        об’єднання   цих  множин  зображатиме  заштрихована  фігура  ( мал.2 ).

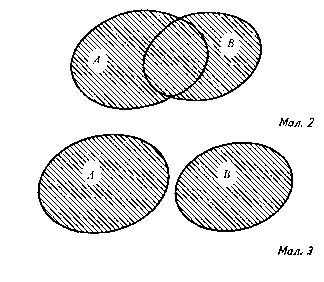
Випадок     об’єднання   множин  А і В, коли  вони  не  мають  спільних  елементів , зображено  на  малюнку  3.  Об’єднання     множин  А і В, якщо

  В ʗ А, зображено  на  малюнку  4

 ( очевидно, А U В = А ).

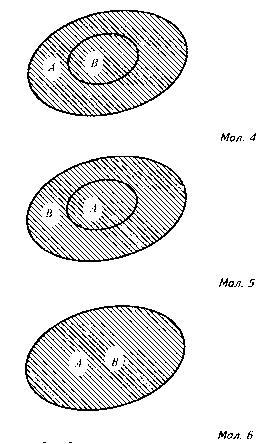
На  малюнку  5  зображено   об‘єднання  множин, коли  А ʗ В ( А U В = В ). Нарешті,  на  малюнку  6  зображено   об‘єднання  множин  А і В, коли  А=В  ( А U В = А U А = А, або  А U В = В U В = В ). Операцію   об‘єднання   множин  можна  виконувати  і  тоді, коли  є  кілька   множин.  На  малюнку  7  зображено  випадок    об‘єднання    трьох  множин  А, В, С.

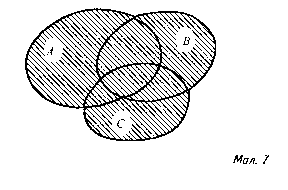
Об‘єднання  цих  множин   позначають     А  U  В  U С.  Аналогічно  можна  ввести  поняття    об‘єднання   чотирьох, п‘яти  та іншої  кількості  множин. Перерізом  двох  множин  А і В називається  множина, що  позначається  А ∩ В, яка  складається  з  тих  і  тільки  тих  елементів, що  належать   до  кожної  з   множин  А і В.  На  малюнку  8  за  допомогою  діаграм  Ейлера – Венна  зображено  переріз  двох  множин  А і В; А ∩ В є множиною  елементів , спільних   для  А і В ( заштрихована  фігура ).

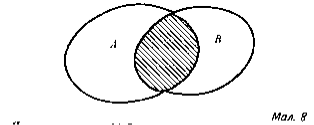
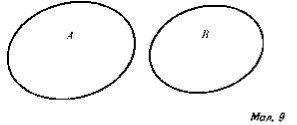
Якщо  множини  А і В  не  мають  спільних  елементів, то  їх  переріз  є  порожньою  множиною  ø ( мал. 9).

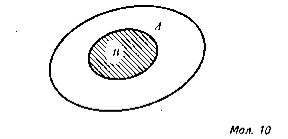
Якщо  В ʗ А, то А ∩ В = В  ( мал.. 10).

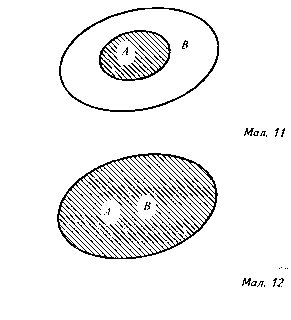
Якщо  А ʗ В, то  А  ∩ В = А (мал. 11). Нарешті, якщо А=В, то А ∩В =А =В (мал..12).

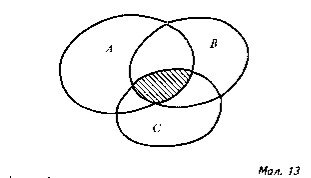
Поняття  перерізу  множин  можна   поширити  на  випадок  кількох  множин. Так, на  малюнку  13  зображено  переріз  трьох  множин  А, В  і С ( цей  переріз  записують  так  А∩В∩С).

Аналогічно  можна  ввести  поняття  перерізу  чотирьох, п ‘яти  та  іншої  кількості  множин.

  РОЗВ’ЯЗУВАННЯ ДЕЯКИХ ТИПІВ ЗАДАЧ

За  допомогою   діаграм  Ейлера -  Венна  можна  розв‘язувати  деякі  типи   задач.

Задача 1. У  деякому класі  20  учнів  захоплюються  спортом , 9 – музикою , 6 – музикою  і  спортом. Визначте  кількість  тих  учнів , які  захоплюються  тільки  спортом , тільки музикою.

Розв’язання

 Множини,  про  які  йдеться  в  задачі,  зобразимо  з допомогою  діаграм  Ейлера – Венна.  Нехай А – множина  учнів, які  захоплюються  спортом ( їх 20 ), В – множина  учнів, які  захоплюються  музикою ( їх 9). Оскільки  є  учні, які   захоплюються  музикою  і  спортом, то  діаграми,які відповідають  множинам  А і В, перетинаються

 ( мал.. 14).

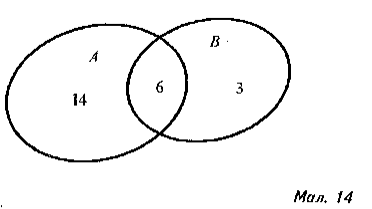
Кожній  з  утворених  нових  діаграм  поставимо  у  відповідність   число – кількість  елементів  множини, зображеної  діаграмою. Одержимо  наочну  картину,  що  дає  можливість  відповісти  на  всі   запитання  задачі.

Відповідь. Кількість  учнів  групи  14+6+3=23;  тільки  спортом  захоплюються  14  учнів, тільки музикою – 3  учні.

Задача 2. У двох  класах  40  учнів. Із  них  30   вміють  плавати, 27 вміють   грати  в  шахи і тільки  четверо  не  вміють  ані  того, ані  іншого. Скільки  учнів  уміють   плавати  і  грати  в  шахи?   Скільки  учнів  уміють   тільки  плавати? Скільки  учнів  уміють   тільки  грати в шахи?

Розв‘язання

Нехай   U – множина  всіх  учнів ( їх 40 ), А – множина  учнів, які  вміють   плавати  ( їх 30 ),  В -  множина   учнів, які  вміють   грати  в шахи ( їх 27 ). Зобразимо  ці  множини  з  допомогою  діаграм  Ейлера – Венна  ( мал. 15).

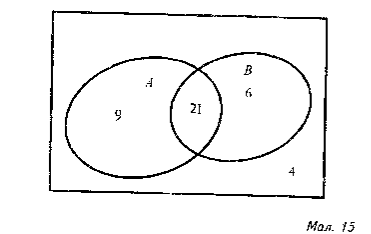
Кожній  з  утворених  діаграм  поставимо  у  відповідність  кількість  елементів  множини, зображеної  відповідною  діаграмою. Оскільки  є  4  учні, які  не  вміють  ані  плавати , ані  грати  в  шахи, то об ‘єднанню   множин  А і В  відповідає  число  40-4 =36. Тоді  перерізу  множин  А і В відповідає   число  (30+27)-36=21.

Відповідь. Плавати  і  грати в шахи  вміє  21  учень. Тільки  плавати  вміють 

30-21=9  учнів. Тільки  грати  в   шахи  вміють  27-21=6  учнів.

Задача 3. Серед  абітурієнтів,  які  витримали  вступні  іспити  в  університет, двадцять  балів  одержали: з  математики  48  абітурієнтів, з  фізики – 37, з української  мови – 42, з математики  або  фізики  (або  з  математики, або з  фізики, або  з  обох  предметів) – 75, з математики  або  з  української  мови  (або  з  математики, або  з  української  мови, або  з  обох  предметів) -76, з фізики або  з  української  мови (або з фізики, або  з  української  мови, або  з  обох  предметів) – 66, з  усіх   трьох  предметів – 4. Скільки   учнів  одержали  двадцять   балів  принаймні  з  одного  предмета?  Скільки   серед  них   одержали  двадцять   балів  тільки  з  одного  предмета? 

Розв‘язання

Нехай  U-множина  всіх  абітурієнтів, М -  множина  абітурієнтів, які  одержали  20  балів з  математики  ( їх 48 ), Ф – множина  абітурієнтів, які  одержали  20   балів  з  фізики  ( їх 37 ), Y – множина  абітурієнтів, які  одержали   20   балів  з  української  мови  ( їх  42 ). Скористаємося  діаграмами  Ейлера – Венна ( мал.. 16). Починаємо  з   останньої  умови  і  рухаємося  до  першої.

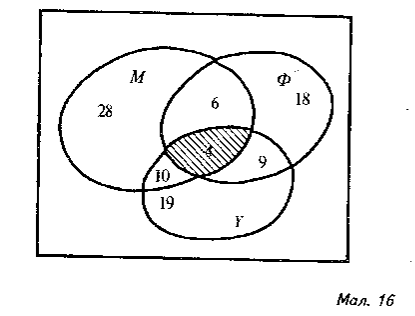
Заштрихованій  діаграмі  відповідає  число 4. У задачі   сказано, що з  математики  або фізики  набрали  20 балів  75  абітурієнтів. Це  означає, що  об’єднання  множин  М і Ф містить  75 елементів. Тоді  переріз  цих  множин   складається з ( 48+37 )- 75=10 елементів. Діаграма, що  відповідає  перерізу  множин  М і Ф, складається  із  заштрихованої  та  не заштрихованої  діаграм. Оскільки  заштрихованій  діаграмі  відповідає  число  4, то  не заштрихованій  – число   10-4=6.  Аналогічно  знаходимо   числа  9 і 10, що  відповідають  незаштрихованим  діаграмам  перерізів  множин  Ф і Y  та Y і М відповідно. Діаграмі, що зображає  множину  абітурієнтів,  які  одержали   20 балів  тільки  з математики, відповідає  число  48-(10+4+6) = 28. Діаграмі, що  зображає  множину  абітурієнтів,   які  одержали  20  балів  тільки  з  фізики, відповідає  число  37-(6+4+9)=18. Діаграмі, що  зображає  множину  абітурієнтів, які  одержали  20 балів   тільки  з  української  мови , відповідає  число          42- (10+4+9 )=19. З допомогою  одержаної  наочної  картини  даємо  відповіді  на  поставлені  в  задачі   питання.

Відповідь. Одержали  20  балів  принаймні  з  одного  предмета  28+6+4+10+19+9+18=94  абітурієнта. Одержали  20  балів  тільки  з  одного  предмета  28+18+19=65 абітурієнтів.

Задача 4. У класі  30  учнів: 5 відмінників, 10  спортсменів  і  15 учасників  художньої  самодіяльності; 2 є  відмінниками  та  спортсменами, 6 – спортсменами  та  учасниками   художньої  самодіяльності, 3-   відмінниками та  учасниками   художньої  самодіяльності, а 1 є  відмінником , спортсменом  і  учасником   художньої  самодіяльності. Визначте:

а) скільки  учнів  не  є  а ні  відмінниками, ані  спортсменами, а ні  учасниками   художньої  самодіяльності;

б) скільки  учнів  є  тільки  відмінниками;

в) скільки  учнів    є  відмінниками або  спортсменами  (принаймні  одне  з  двох);

г) скільки  учнів    є  відмінниками або  спортсменами   (тільки  одне з  двох ).

Розв‘язання

Нехай  U- множина  учнів  класу (їх 30), А – множина   відмінників ( їх 5), В – множина  спортсменів (їх 10), С  - множина  учасників  художньої  самодіяльності

 ( їх 15). Починаючи  з  останньої умови і  рухаючись  до  першої, зображаємо  з допомогою  діаграм  Ейлера –Венна  множини, про  які  йдеться   в  задачі ( мал..17).

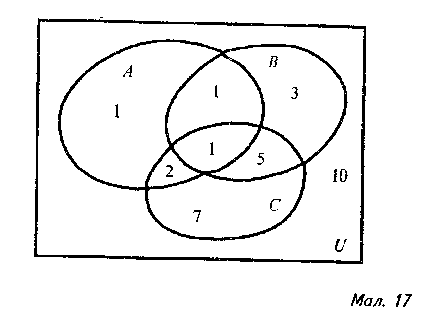
У кожну  діаграму  вписуємо  відповідне  число. Користуючись  наочним  зображенням   даємо відповідь  на  поставлені  запитання.

Відповідь. а) 10;  б)1;  в)13; г)11.

Задача 5. Серед   150  учнів  тільки  хлопці  збирають  марки.  67  хлопців  збирають  марки   України, 48- Африки, 32- Америки, 11  учнів  -  тільки  України , 7 – тільки  Африки, 4 учні – тільки  Америки  і  лише  Карпенко  збирає  марки  України, Африки і Америки. Знайдіть  максимальну  кількість  дівчат.

Розв‘язання

Нехай   U – множина  всіх  учнів  (їх 150 ),  А – множина  хлопців,  які  збирають  марки   Африки  (їх 48), В – множина  хлопців, які  збирають  марки  України  (їх 67), С – множина  хлопців, які  збирають  марки  Америки  ( їх 32).  З допомогою  діаграм  Ейлера-Венна  наочно  зображаємо  множини, про  які  йдеться  в  задачі. Одержаним  новим  діаграмам  ставимо  у відповідність  числа  так, як  показано   на  малюнку   18.

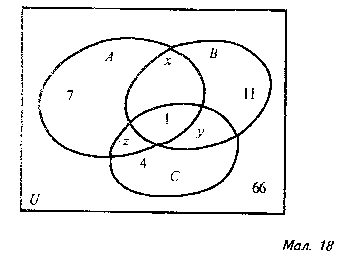
Маємо:

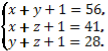
Додавши  почленно  ці  рівності , одержуємо:

Х+У+Z=61.

Отже, марки  збирають    61+1+7+11+4=84  хлопці.  Максимальна  кількість  дівчат  становить:         150-84=66.

Відповідь. 66 дівчат.