Матеріали для підготовки до ЗНО з математики
Стереометрія
Основні положення
1) Якщо пряма, що перетинає деяку площину, перпендикулярна двом прямим в цій площині, що проходять через точку перетину, то вона перпендикулярна цій площині (ознака перпендикулярності прямої та площини).
2) Якщо дві різні прямі перпендикулярні одній площині, то вони паралельні.
3) Пряма, проведена на площині через основу похилої перпендикулярно до її проекції, перпендикулярна і самій похилій. І навпаки, якщо пряма на площині перпендикулярна похилій, то вона перпендикулярна і проекції цієї похилої (теорема про три перпендикуляри).
4) Якщо площина проходить через пряму, що є перпендикулярною іншій площині, то ці площини перпендикулярні.
5) Якщо ![]() – площа многокутника, а
– площа многокутника, а ![]() – площа проекції цього многокутника на деяку площину
– площа проекції цього многокутника на деяку площину ![]() , то має місце співвідношення
, то має місце співвідношення ![]() , де
, де ![]() – кут між площиною многокутника і площиною
– кут між площиною многокутника і площиною ![]() .
.
Многогранники
Означення 1. Призма – це многогранник, який складається з двох плоских многокутників, що суміщаються паралельним перенесенням, і усіх відрізків, що сполучають відповідні точки цих многокутників.
Відрізки, які з’єднують відповідні вершини многокутників (основ призми), називаються бічними ребрами. Якщо бічні ребра призми перпендикулярні основам, то така призма називається прямою. Якщо, при цьому, основами призми є правильні многокутники, то призма є правильною.
Об’єм призми можна знайти за такими формулами:
1) ![]() , де
, де ![]() – площа основи призми;
– площа основи призми; ![]() – висота призми.
– висота призми.
2) ![]() , де
, де ![]() – площа перерізу, перпендикулярного ребрам,
– площа перерізу, перпендикулярного ребрам, ![]() – бічне ребро.
– бічне ребро.
3) якщо призма правильна, то ![]() .
.
Площа бічної поверхні призми обчислюється за формулою:
![]() , де
, де
![]() – периметр перпендикулярного перерізу до бічних ребер.
– периметр перпендикулярного перерізу до бічних ребер.
У випадку прямої призми формула набуває вигляду: ![]() , де
, де ![]() – периметр основи призми.
– периметр основи призми.
Повна поверхня призми дорівнює сумі бічної поверхні та площі основ, тобто: ![]() .
.
 Означення 2. Пірамідою називається многогранник, який складається з плоского многокутника – основи піраміди, точки, що не лежить в площині основи, – вершини піраміди та усіх відрізків, що сполучають вершину з точками основи.
Означення 2. Пірамідою називається многогранник, який складається з плоского многокутника – основи піраміди, точки, що не лежить в площині основи, – вершини піраміди та усіх відрізків, що сполучають вершину з точками основи.
Відрізки, що сполучають вершину піраміди з вершинами основ, називаються бічними ребрами.
Якщо основою піраміди є правильний многокутник, а проекція вершини на площу основи співпадає з центром основи, то така піраміда називається правильною.
Об’єм піраміди знаходиться за формулою:
![]() , де
, де
![]() – площа основи,
– площа основи, ![]() – висота піраміди.
– висота піраміди.
Бічна поверхня ![]() правильної піраміди і повна поверхня
правильної піраміди і повна поверхня ![]() довільної піраміди знаходяться за формулами:
довільної піраміди знаходяться за формулами:
![]() , де
, де
![]() – периметр основи піраміди,
– периметр основи піраміди, ![]() – апофема бічної грані (відрізок
– апофема бічної грані (відрізок ![]() на рис 5.2.2).
на рис 5.2.2).

![]() .
.
Об’єм зрізаної піраміди (рис 5.2.3) обчислюється за формулою:
![]() , де
, де
![]() – висота зрізаної піраміди,
– висота зрізаної піраміди,
![]() – площі відповідно верхньої та нижньої основ піраміди.
– площі відповідно верхньої та нижньої основ піраміди.
Площа бічної поверхні правильної зрізаної піраміди обчислюється за формулою:
![]() , де
, де
![]() – апофема бічної грані,
– апофема бічної грані, ![]() – периметри нижньої та верхньої основ.
– периметри нижньої та верхньої основ.
Завдання для самостійного розв’язування
1.
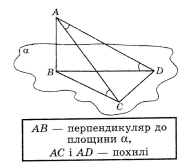
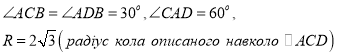
Знайти ![]() .
.
2.
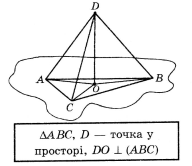
![]()
Знайти ![]() .
.
3.

![]()
Знайти ![]() .
.
4.
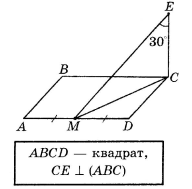
![]()
Знайти ![]() .
.
5.
![]()
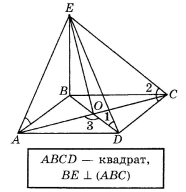 Знайти
Знайти ![]() .
.
6.
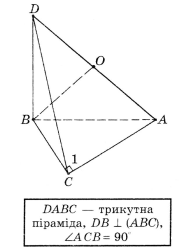
![]()
Знайти ![]() .
.
7.
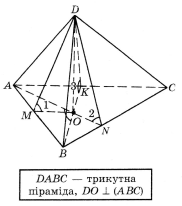
![]()
Знайти ![]() .
.
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 8.
8.
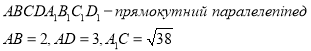
Знайти ![]() .
.

![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 9.
9.
![]()
![]()
Знайти ![]() .
.
10.
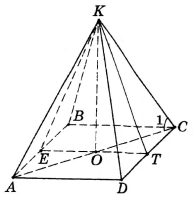
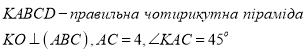
Знайти ![]() .
.
11. У прямокутному паралелепіпеді довжини основ відповідно рівні ![]() і
і ![]() . Діагональ паралелепіпеда складає з площиною основи кут
. Діагональ паралелепіпеда складає з площиною основи кут ![]() . Знайти бічну поверхню паралелепіпеда.
. Знайти бічну поверхню паралелепіпеда.
Відповідь: ![]() .
.
12. Бічне ребро правильної чотирикутної піраміди, довжиною ![]() , складає з площиною основи кут
, складає з площиною основи кут ![]() . Знайти об’єм піраміди.
. Знайти об’єм піраміди.
Відповідь: 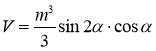 .
.
Домашнє завдання
1.
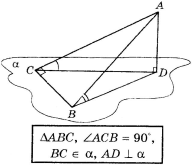
![]()
Знайти ![]() .
.
2.
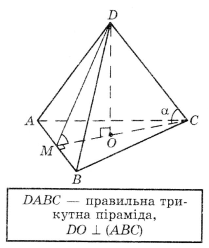
![]()
Знайти ![]() .
.

![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 3.
3.
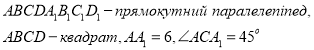
Знайти ![]() .
.
4.
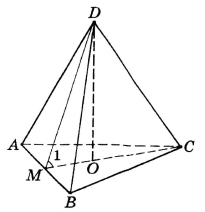
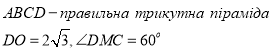
Знайти ![]() .
.
5. Об’єм правильної чотирикутної піраміди ![]() . Кут нахилу її бічного ребра до площини основи
. Кут нахилу її бічного ребра до площини основи ![]() . Знайти бічне ребро піраміди.
. Знайти бічне ребро піраміди.
Відповідь: 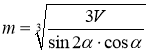 .
.


про публікацію авторської розробки
Додати розробку
