Геометрія 10 клас

 Розділ. КООРДИНАТИ І ВЕКТОРИ.

Тема: Симетрія відносно початку координат та осей, координатних площин

(Матеріали для проведення уроку з геометрії 10 клас, на основі підручника Математика 10 клас автор Бевз)

 Поняття симетрії відносно точки у просторі.

Точки A і A' називають симетричними відносно точки O, якщо точка O — середина відрізка AA'. Перетворенням симетрії відносно точки O (центральною симетрією) називають таке перетворення, при якому кожна точка даної фігури переходить у точку, симетричну їй відносно точки O.

Якщо симетрія відносно точки O переводить дану фігуру в ту саму фігуру, то таку фігуру називають центральносиметричною, а точку O — її центром симетрії. Прикладом такої фігури є прямокутний паралелепіпед. Його центр симетрії — точка перетину діагоналей паралелепіпеда.

1.     Поняття симетрії відносно прямої у просторі.

Точки A і A' називають симетричними відносно прямої l, якщо ця пряма перпендикулярна до відрізка AA' і проходить через його середину.

Перетворенням симетрії відносно прямої (осьовою симетрією) нназивають таке перетворення, при якому кожна точка фігури переходить у точку, симетричну їй відносно даної прямої. Наприклад, куб має вісь симетрії, причому не одну.

2.     Поняття симетрії відносно площини у просторі.

Точки A і A' називають симетричними відносно площини α, якщо ця площина перпендикулярна до відрізка AA' і проходить через його середину (рис. 1). Точки площини α вважаються симетричними самі до себе. При цьому площину α називають площиною   симетрії.

Перетворенням симетрії відносно площини α називають таке перетворення, при якому кожна точка даної фігури переходить у точку, симетричну їй відносно площини α. Якщо перетворення симетрії відносно площини α переводитьдану фігуру в себе, то таку фігуру називають симетричною відносно площини α. Наприклад, куля є симетричною відносно будь-якої площини, яка проходить через її центр.

Учитель пропонує учням ознайомитися з таблицею, заздалегідь підготовленою на дошці, і сформувати уявлення про те, що точки, симетричні точці A(x;y;z) відносно початку координат,координатних осей і площин, мають такі координати.

Для закріплення матеріалу перегляньте відео за посиланням:

https://www.youtube.com/watch?v=uXKrjcmDg6w&ab_channel=%D0%A2%D0%BE%D0% BF%D0%A8%D0%BA%D0%BE%D0%BB%D0%B0

Розв'язання задач:

§  ЗАДАЧА 1. Точки A і B симетричні відносно точки C. Знайдіть координати точки C, якщо A(5;-3;4) і B(-3;1;-2). Відповідь: C(1;-1;1).

§  ЗАДАЧА 2. Точку M (a;b;c) послідовно симетрично відобразили відносно координатних площин Oxy, Oxz, Oyz. Доведіть, що отримана при цьому точка M' симетрична точці M відносно початку координат.

Доведення: Точка M (a;b;c) при симетрії відносно площини Oxy переходить у точку N (a;b;-c). Точка N (a;b;-c) − при симетрії відносно площини Oxz переходить у точку K (a;b;-c).Точка K (a;-b;-c) при симетрії відносно площини Oyz переходить у точку M' (-a;-b;-

c). Середина відрізка MM' має координати (0;0;0). Отже, початок координат — центр симетрії точок M і M'.

§  ЗАДАЧА 3. Точка A(5;2;3) належить колу із центром O. Знайдіть радіус кола, якщо при симетрії відносно осі ординат центр кола переходить у точку O(-2;1;1).

Розв’язання: Оскільки точка O при симетрії відносно осі ординат перейшла в точку O′(−2;1;1),то точка O має координати: O(2;1;−1).

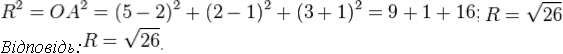
§  ЗАДАЧА 4. Дано точки  і  Знайдіть координати точки, симетричної середині відрізка AB відносно: а) точки ; б) осі аплікат; в) площини Oxy.

Розв’язання:

а)                  Знайдемо                  середину                  відрізка                  AB                —

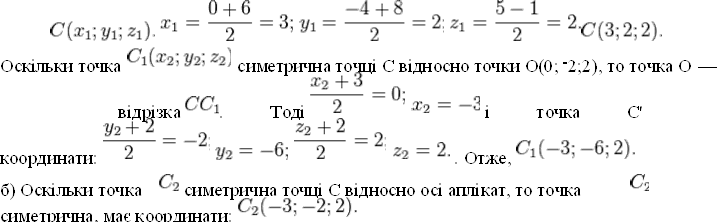точку                                                                                                                             

середина                                                                                                                         має

, яка їй

в) Точка  симетрична точці C відносно площини Oxy, має координати:  

Відповідь:  

Домашнє завдання:  §35

Виконайте № 1275, 1276