Матеріали до теми "Системи лінійних рівнянь"
Матеріали до теми "Системи лінійних рівнянь" для 9-го класу містять розробку теоретичних карток-консультантів, а також різні види перевірочних робіт: усні вправи, математичні диктанти, самостійні та контрольні роботи, подані у двох рівнях складності.
Матеріали до теми «Системи лінійних рівнянь»
Розв'язання лінійних рівнянь з двома змінними (окремі випадки)
ax + by + c = 0
|
№ |
Умова |
Вигляд рівняння |
Розв'язки |
Графічне зображення |
|
|
a=0,b=0,c=0 |
y = - ax / b – c / b |
Пряма
|
|
|
|
a=0,b=0 |
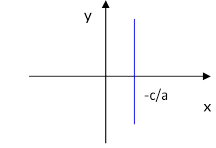
x = - c / a |
Пряма паралельна осі ординат, що перетинає вісь абсцис у точці x = -c / a |
|
|
|
a=0 |
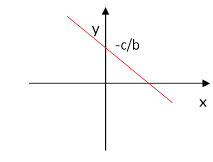
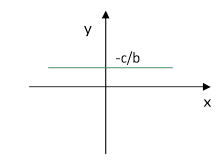
y = - c / b |
Пряма паралельна осі абсцис, що перетинає вісь ординат у точці y = - c / b |
|
|
|
a=0,b=0,c=0 |
0 = 0 |
Будь-яка точка координатної площини |
|
|
|
a=0,b=0,c=0 |
c = 0 |
Немає жодного розв'язку. |
|
Кількість розв'язків системи лінійних рівнянь
![]() а1x
+ b1y = c1 а2x + b2y = c2
а1x
+ b1y = c1 а2x + b2y = c2
1. Система не має розв'язків, якщо a 1 = = b1 c1
a2 b2 c2
2. Система має єдиний розв'язок, якщо a1 = b1
a2 b2
3. Система має нескінченне число розв'язків, якщо a1 = = b1 c1 a2 b2 c2
Типи систем лінійних рівнянь з двома змінними.
|
Типи систем |
|
Приклади |
|
|
|
0х + 0у = 1 0х + 0у = 2 |
|
Система не має розв'язків |
|
вся площина жодної точки
|
0х + 0у = 0 0х + 0у = -1 |
|
Система не має розв'язків |
|
|
0х + 0у = 0 0х + 0у = 0
|
|
Будь-яка пара чисел |
|
пряма
|
0х + 0у = 6 2х + 3у = 5
|
|
Система не має розв'язків |
|
пряма
|
2х + 7у = 5
|
|
Координати будь-якої точки прямої |
|
дві прямі, що перетинаються
|
х + у = 0 х + 3у = 4
|
|
Єдиний розв'язок – координати точки перетину прямих |
|
|
х + у = 0 х + у = 1
|
|
Система не має розв'язків |
|
які співпадають
|
х + у = 0 2х + 2у = 0 |
|
Координати будь-якої точки прямої |
Картка – консультант
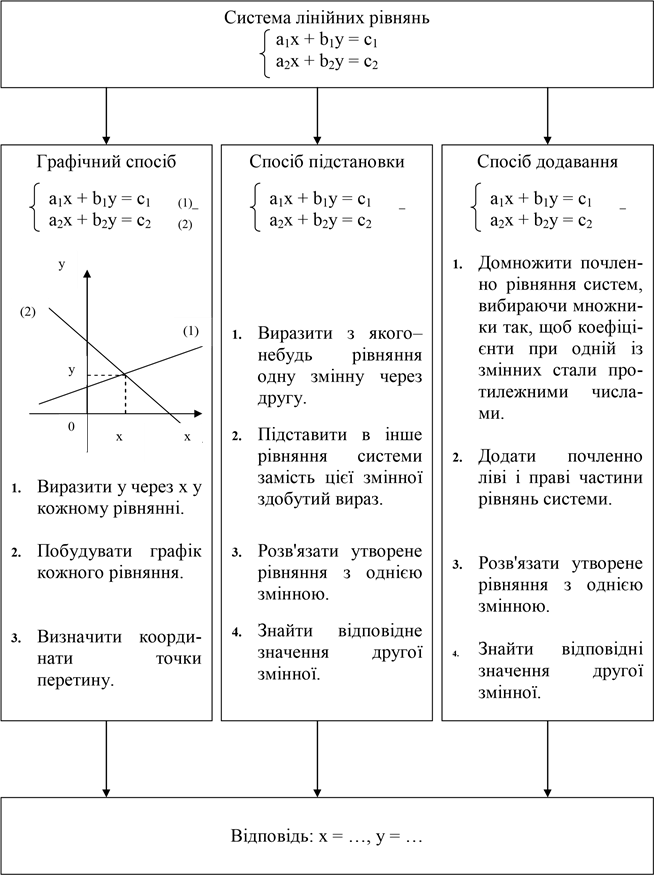
Усні вправи
1. Виразити змінну у через змінну х:
а) х + у = 7, б) 3х – 2у = 4, в) 0,5у – 3х = 0
2. Наведіть приклад лінійного рівняння із змінними у і х, яке має ту саму множину розв'язків, що й рівняння:
а) х – у = 5, в) 2х + у = 8.
3. Назвіть кілька розв'язків рівнянь:
а) 0х + 3у = 6, б) х + 0у = 7.
Що являє собою графік кожного з рівнянь?
4. Чи має система розв'язки? Якщо має, то скільки?
![]()
![]()
![]() а) у = 2х – 7 б)
у = х – 1 в) у = 2х + 1,5
а) у = 2х – 7 б)
у = х – 1 в) у = 2х + 1,5
у = 3х у = х + 3 2у = 4х + 3
5. Що являє собою графік рівняння?
(х – 2)2 + (у + 3)2 = 0
6. Чи проходить через точку А (2; 6) пряма:
а) у – 2х = 10, б) 2у – 3х = 6, в) х + 0у = 2?
7. Розв'яжіть систему рівнянь:
![]()
![]() а) б) х = 3 х –
3у = 5
а) б) х = 3 х –
3у = 5
2х – у = 8 у = 0,5
8.
![]() Підберіть такі значення а і с, при
яких система 2х – у = 4
Підберіть такі значення а і с, при
яких система 2х – у = 4
ах – у = с
а) має єдиний розв’язок, б) не має розв’язку, в) має безліч розв’язків.
9. В якій точці перетинаються прямі: х + 3у = 0 і 2х + 7у = 0?
10. Що являє собою графік рівняння:
а) ху = 8, б) ху = 0?
11. Знайдіть область визначення виразу:
а) а2, б) 6 – а, в) 1/а, г) 3 : (а – 4), д) (а – 1) : (а + 5)
12. Чи має розв’язок рівняння х2 + (у + 2)2 = 0?
13.
 Чи має розв’язок система х2
+ (у + 2)2 = 0 х + 2у = 5
Чи має розв’язок система х2
+ (у + 2)2 = 0 х + 2у = 5
14. Розв'яжіть рівняння у – 3 + х – 6 = 0
15. Складіть систему рівнянь за умовою задачі: На двох полицях 60 книжок. На другій полиці на 10 книжок менше, ніж на першій. Скільки книжок на кожній полиці?
Математичні диктанти.
І. Число розв'язків системи рівнянь
1. При розв'язуванні системи двох лінійних рівнянь з двома змінними можуть трапитися такі випадки…
2. Назвіть умови, при яких прямі: у = k1x – 2 і y = k2x + 2 а) перетинаються, б) паралельні.
3.
![]() Знайдіть такі значення а, b, с, щоб
система 2х – у = 5 мала нескінченну множину
розв'язків. ах + bу =
с
Знайдіть такі значення а, b, с, щоб
система 2х – у = 5 мала нескінченну множину
розв'язків. ах + bу =
с
4.
![]() Розв'яжіть систему у =х
Розв'яжіть систему у =х
2х + 3у = 15
ІІ Найпростіші системи. Спосіб додавання. Спосіб підстановки.
1. Чи є пара (2,5; 0) розв'язком системи 2х + 10у = 0
2х + 5у = 5
2. Розв'яжіть способом додавання 5х + 2у = 10
7х – 2у = 14
3. Розв'яжіть способом підстановки 3х – у = 10
5х + 2у = 13
4.
![]() Розв'яжіть систему графічним
способом у = х у = -х + 1
Розв'яжіть систему графічним
способом у = х у = -х + 1
5. Відомо, що 30% числа а на 10 більше 20% числа b, а 150% числа b дорівнює числу а. Знайти а і b.
ІІІ Окремі випадки систем. Розв'язування задач складанням систем.
1.
![]()
![]() Розв'яжіть систему: а)
у = х в) у = -2х
Розв'яжіть систему: а)
у = х в) у = -2х
2х + 3у = 5,5 х – 3у = 7
2. Число 10 розділить на такі дві частини, щоб різниця їх становила 5. Знайти частини.
3. Є певна кількість кролів і півнів. У них разом п'ятдесят голів, Сто двадцять ніг. Скільки є кролів і півнів.
Самостійна робота №1
|
Варіант 1 |
Варіант 2 |
|
10. Знайти п'ять будь-яких розв'язків рівняння і позначити на координатній площині відповідні їм точки (2 бали) |
|
|
х + 2у = 7
|
х – 2у = 1 |
|
20. Які з пар чисел є розв'язком рівняння (2 бали) |
|
|
5у – 2х = 26 (5; 2), (-3; 4), (8; 0)
|
7х – 3у = 15 (3; 2), (-3; 2), (0; -5) |
|
30. Побудуйте графік функції (2 бали) |
|
|
2х – у = 6
|
4х – у =8 |
|
4 .Чи мають розв'язки рівняння (2 бали) |
|
|
а) х2 + (-у)2 = - 9 б) х2 + у2 = 0 в) (3 – х)2 + (1 - у)2 = -1 |
а) у2 + (-х)2 = - 4 б) х2 + у2 = 8 в) (1 – х)2 + (у - 2)2 = -3 |
|
5. При якому значенні а графік рівняння проходить через початок координат? (2 бали) |
|
|
3х – 7у = а
|
6х + 7у = а + 4 |
|
6. Знайти абсцису точки К, якщо: (2 бали) |
|
|
графік рівняння 2у – 3х = 7 проходить через точку К, ордината якої дорівнює 5 |
графік рівняння 5х – 2у = -11 проходить через точку К, ордината якої дорівнює 3 |
Самостійна робота №2
|
Варіант 1 |
Варіант 2 |
|
1. Чи є пара чисел розв'язком системи рівнянь |
|
|
|
2ху = 6 |
|
2. Знайдіть розв'язок системи рівнянь графічним способом |
|
|
3х – у = -5 |
-2х – у = -7 |
|
3. Скільки розв'язків має система рівнянь? |
|
|
-6х + 3у = 2 |
15х – 6у = -21 |
|
4. Дано перше рівняння системи. Знайдіть друге рівняння системи так, щоб вона мала єдиний розв'язок |
|
|
х – у = 2
|
2х + у =4 |
|
5. Складіть яку-небудь систему рівнянь з двома змінними розв'язками, якої є пара значень змінних: |
|
|
х = 5; у = 2
|
х =4; у = 3 |
Самостійна робота №3

Самостійна робота №4
|
Варіант 1 |
Варіант 2 |
|
ОСНОВНИЙ РІВЕНЬ |
|
|
1. Розв'язати способом додавання систему рівнянь: |
|
|
|
а – б = 6 3х – 5у = 1 |
|
2. З'ясувати, чи має розв'язок система) |
|
|
-6х – 14у = 32 |
-8х – 2у = -14 |
|
3. Розв'язати систему рівнянь |
|
|
56 – (4х – 2у) = 2(2х + 5у) 5(х – у) – 2(2х – у) = - 8 |
|
|
ПІДВИЩЕНИЙ РІВЕНЬ |
|
|
1. Розв'язати способом додавання систему рівнянь: |
|
|
2х – у = -7 |
3х – 6у = 4 |
|
2. Розв'язати систему рівнянь із змінними, якщо одним із розв'язків першого рівняння є перша пара, а другого – друга пара чисел |
|
|
2х + 6у = 5 |
2х + 6у = 5 |
|
3. Розв'язати систему |
|
|
(х – у + 1) : 3 – (х + у – 1) : 4 = -3 |
(2х + у) : 2 – (х + 2у) : 3 = 1/3
|
Тематична контрольна робота №1
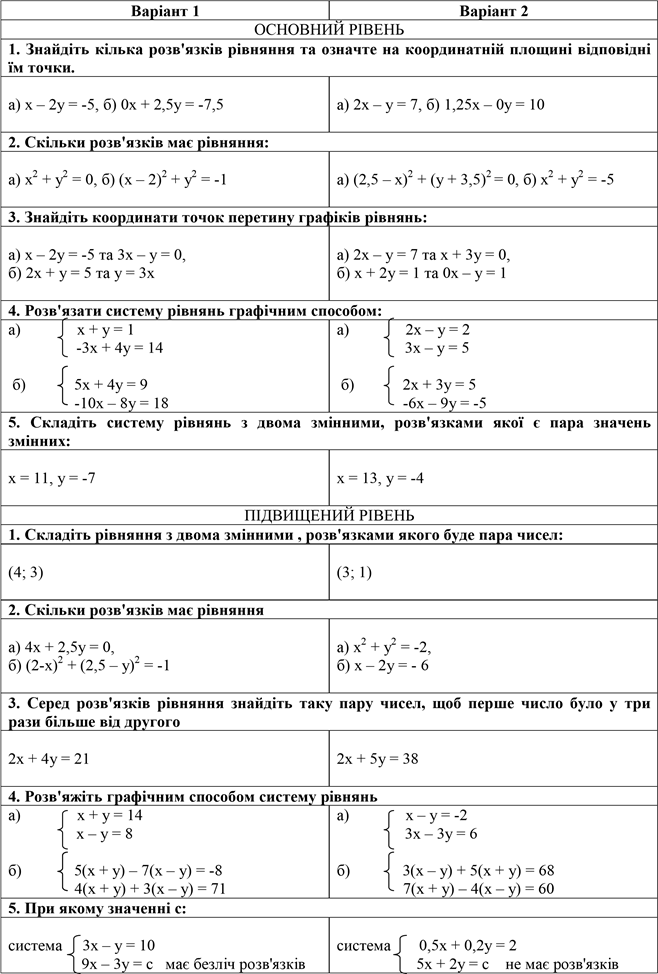
Тематична контрольна робота №2
|
Варіант 1 |
Варіант 2 |
|
1. Розв'яжіть систему рівнянь: |
|
|
х + у = 5 3х + у = 7
б) способом додавання (2 бали) 2х + 3у = 7 7х – 3у = 11
|
х - у = 3 2х - у = 8
б) способом додавання (2 бали) 4х + 5у = 2 3х – 5у = 19
|
|
2.
За 5 кг апельсинів і 4 кг лимонів заплатили 22 грн., а за 6 кг апельсинів та 2 кг лимонів – 18 грн. Скільки коштує один кілограм апельсинів? Скільки коштує один кілограм лимонів?
(2 бали) |
2.
За 4 зошити і 3 авторучки заплатили 13 грн., а 8 зошитів і 5 авторучок заплатили 23 грн. Скільки коштує один зошит? Скільки коштує одна авторучка?
(2 бали) |
|
3. Розв'язати систему рівнянь: (2 бали) |
|
|
(3х – 1) : 10 – (4у + 1) : 5 = -3 (2х + 1) : 3 – (3у – 2) : 8 = 3
|
(5х + 1) : 8 – (у + 16) : 5 = -1 (7х – 1) : 4 – (3у + 13) : 5 = 13 |
|
4.
За 5 годин за течією і 3 години проти течії теплохід пройшов 230 км. Знайти власну швидкість теплохода і швидкість течії, якщо за 2 години за течією і 7 годин проти течії, теплохід проходить 278 км?
(3 бали) |
4.
За 5 годин за течією і 3 години проти течії теплохід пройшов 244 км. Знайти власну швидкість теплохода і швидкість течії, якщо за 2 години за течією і 30 хвилин проти течії, теплохід проходить 78 км?
(3 бали) |
|
5. Розв'язати систему рівнянь з двома змінними: (1 бал) |
|
|
2х - 3у = 1
|
4у – 10х = 3 |


про публікацію авторської розробки
Додати розробку

-

Андрій Мірошник
28.02.2018 в 12:46
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Артем Битько
28.02.2018 в 12:46
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Ростислав Дмитренко
28.02.2018 в 12:45
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Данило Байрак
28.02.2018 в 12:44
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 1 відгук