Завдання.Визначте відповідність залежностей v (t) , наведених у  стовпчику А (табл.1 – І варіант, табл. 2 – ІІ варіант), та  x (t) , наведених у  стовпчику Б (табл.1 – І варіант, табл. 2 – ІІ варіант).  Дайте розгорнутий аналіз графіків №№1-5 зі стовпчика А. Запишіть формули залежностей v (t)  та  x (t) . Узагальніть відповіді   у вигляді:

1   (стовпчик А) – цифра (стовпчик Б)

2   (стовпчик А) – цифра (стовпчик Б)

3   (стовпчик А) – цифра (стовпчик Б)

4   (стовпчик А) – цифра (стовпчик Б) 5 (стовпчик А) – цифра (стовпчик Б)

 

 

 

 

 

 

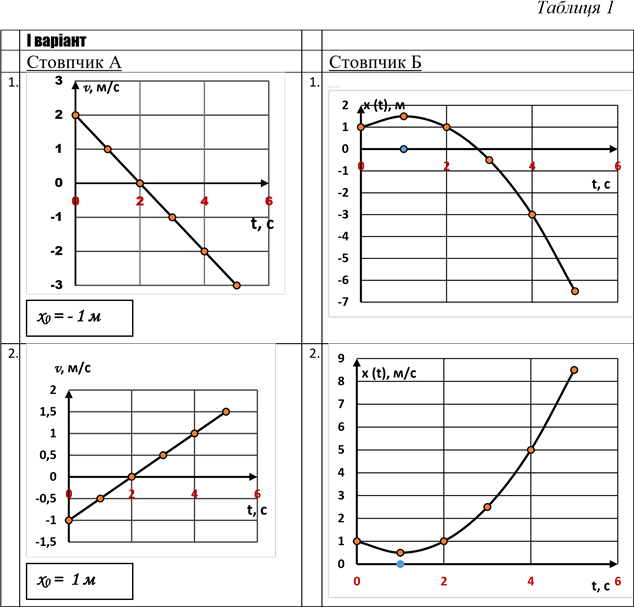
Розв’язання завдань І варіанта, наведених в табл. 1.

Графік №1, стовпчик А V₀=2 м/с

t_в=2 с – зміна напрямку руху, абсциса вершини параболи x₀ = - 1 м

м

(𝟎 −𝟐 𝒄𝟐) ^с = −𝟏 см_𝟐

𝒂_𝒙 =

𝑣(𝑡) = 𝑣₀ ± 𝑎𝑡

𝑣(𝑡) = 2 − 𝑡 = − 𝑡 + 2

𝑎𝑡²

𝑥(𝑡) = 𝑥₀ ± 𝑣₀𝑡 ±  

2

𝑥(𝑡) = −1 + 2𝑡 − 0,5𝑡² = − 0,5𝑡² + 2𝑡 − 1

Аналіз коефіцієнтів квадратного рівняння (𝑦(𝑥) = 𝑎𝑥² + 𝑏𝑥 + 𝑐 )

	a, гілки вниз	b= -2 а*tв (tв =2 с)	c (x0 = - 1 м)
Значення	-0,5	2	-1
Знак	<0	>0	<0

 

Ордината вершини параболи 𝑥(𝒕в)

𝑥(2 𝑐) = = − 0,5 ∗ 2² + 2 ∗ 2 − 1 = 1 м > 0

Відповідь: графіку №1 залежності v (t)  ( стовпчик А, табл. 1) відповідає графік №3 залежності x (t)   ( стовпчик Б, табл. 1).

Графік №2, стовпчик А

V₀= -  1 м/с

t_в=2 с – зміна напрямку руху, абсциса вершини параболи x₀ = 1 м

м

(𝟎 − 𝟐(− 𝒄𝟏)) ^с = 𝟎, 𝟓 см_𝟐

𝒂_𝒙 =

𝑣(𝑡) = 𝑣₀ ± 𝑎𝑡

𝑣(𝑡) = −1 + 0,5𝑡 = 0,5 𝑡 − 1

𝑎𝑡²

𝑥(𝑡) = 𝑥₀ ± 𝑣₀𝑡 ±  

2

𝑥(𝑡) = 1 − 𝑡 + 0,25𝑡² = 0,25𝑡² − 𝑡 + 1

Аналіз коефіцієнтів квадратного рівняння (𝑦(𝑥) = 𝑎𝑥² + 𝑏𝑥 + 𝑐 )

	a, гілки вверх	b= -2 а*tв (tв =2 с)	c (x0 = 1 м)
Значення	0,25	-1	1
Знак	> 0	< 0	> 0

 

Ордината вершини параболи 𝑥(𝒕в)

𝑥(2 𝑐) = = 0,25 ∗ 2² − 2 + 1 = 0 м

Відповідь: графіку №2 залежності v (t)  ( стовпчик А, табл. 1) відповідає графік №5 залежності x (t)   ( стовпчик Б, табл. 1).

Графік №3, стовпчик А V₀= 1м/с

t_в= 1с – зміна напрямку руху, абсциса вершини параболи x₀ = 1 м

м

(𝟎 −𝟏 𝒄𝟏) ^с = −𝟏 см_𝟐

𝒂_𝒙 =

𝑣(𝑡) = 𝑣₀ ± 𝑎𝑡

𝑣(𝑡) = 1 − 𝑡 = − 𝑡 + 1

𝑎𝑡²

𝑥(𝑡) = 𝑥₀ ± 𝑣₀𝑡 ±  

2

𝑥(𝑡) = 1 + 𝑡 − 0,5𝑡² = − 0,5𝑡² + 𝑡 + 1

Аналіз коефіцієнтів квадратного рівняння (𝑦(𝑥) = 𝑎𝑥² + 𝑏𝑥 + 𝑐 )

	a, гілки вниз	b= -2 а*tв (tв =1 с)	c (x0 = 1 м)
Значення	-0,5	1	1
Знак	< 0	> 0	> 0

 

Ордината вершини параболи 𝑥(𝒕в)

𝑥(1 𝑐) = = − 0,5 ∗ 1² + 1 + 1 = 1,5 м > 0

Відповідь: графіку №3 залежності v (t)  ( стовпчик А, табл. 1) відповідає графік №1 залежності x (t)   ( стовпчик Б, табл. 1).

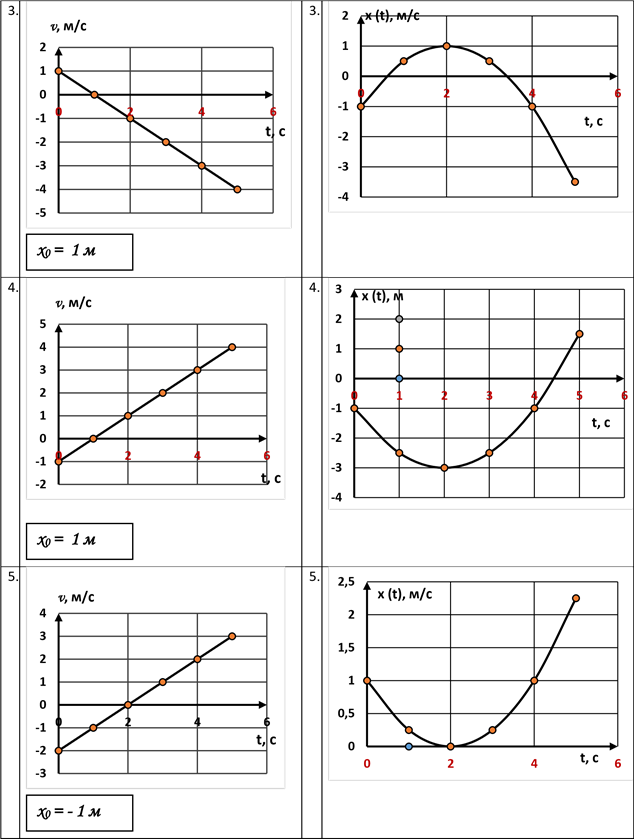
Графік №4, стовпчик А

V₀= -1м/с

t_в= 1с – зміна напрямку руху, абсциса вершини параболи x₀ = 1 м

м

(𝟎 − 𝟏(− 𝒄𝟏)) ^с = 𝟏 см_𝟐

𝒂_𝒙 =

𝑣(𝑡) = 𝑣₀ ± 𝑎𝑡

𝑣(𝑡) = −1 + 𝑡 = 𝑡 − 1

𝑎𝑡²

𝑥(𝑡) = 𝑥₀ ± 𝑣₀𝑡 ±  

2

 

𝑥(𝑡) = 1 − 𝑡 + 0,5𝑡² = 0,5𝑡² − 𝑡 + 1

Аналіз коефіцієнтів квадратного рівняння (𝑦(𝑥) = 𝑎𝑥² + 𝑏𝑥 + 𝑐 )

	a, гілки вверх	b= -2 а*tв (tв =1 с)	c (x0 = 1 м)
Значення	0,5	-1	1
Знак	> 0	< 0	> 0

 

Ордината вершини параболи 𝑥(𝒕в)

𝑥(1 𝑐) = = 0,5 ∗ 1² − 1 + 1 = 0,5 м > 0

Відповідь: графіку №4 залежності v (t)  ( стовпчик А, табл. 1) відповідає графік №2 залежності x (t)   ( стовпчик Б, табл. 1).

 

Графік №5, стовпчик А

V₀= - 2 м/с

t_в=2 с – зміна напрямку руху, абсциса вершини параболи x₀ = - 1 м

м

(𝟎 − 𝟐(− 𝒄𝟐)) ^с = 𝟏 см_𝟐

𝒂_𝒙 =

𝑣(𝑡) = 𝑣₀ ± 𝑎𝑡

𝑣(𝑡) = −2 + 𝑡 = 𝑡 − 2

𝑎𝑡²

𝑥(𝑡) = 𝑥₀ ± 𝑣₀𝑡 ±  

2

𝑥(𝑡) = −1 − 2𝑡 + 0,5𝑡² = 0,5𝑡² − 2𝑡 − 1

Аналіз коефіцієнтів квадратного рівняння (𝑦(𝑥) = 𝑎𝑥² + 𝑏𝑥 + 𝑐 )

	a, гілки вверх	b= -2 а*tв (tв =2 с)	c (x0 = - 1 м)
Значення	0,5	- 2	-1
Знак	> 0	< 0	< 0

 

Ордината вершини параболи 𝑥(𝒕в)

𝑥(2 𝑐) = = 0,5 ∗ 2² − 2 ∗ 2 − 1 = −3 м <  0

Відповідь: графіку №5 залежності v (t)  ( стовпчик А, табл. 1) відповідає графік №4 залежності x (t)   ( стовпчик Б, табл. 1).

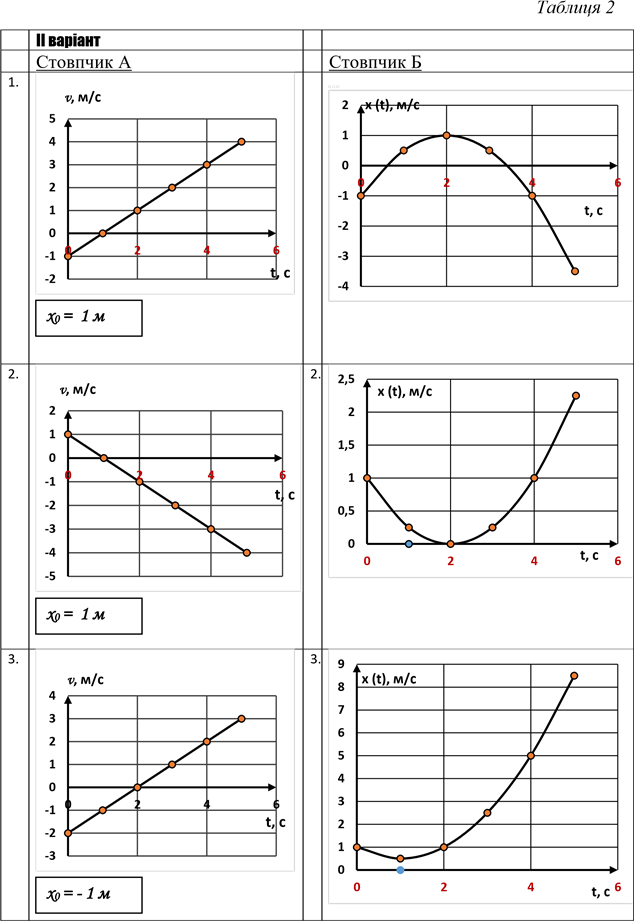
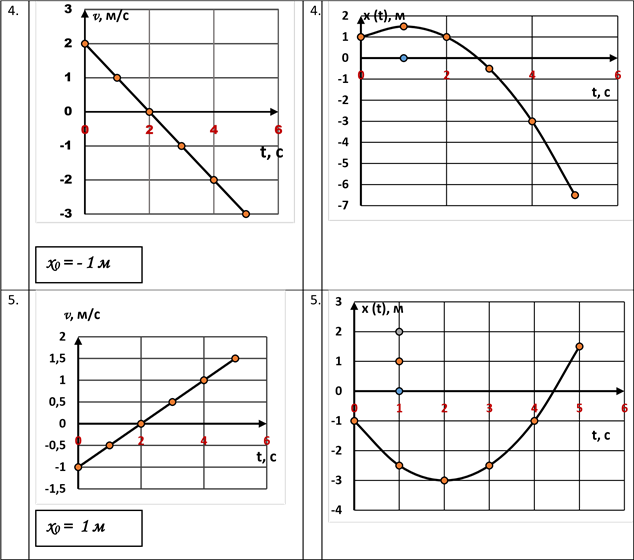
Розв’язання завдань ІІ варіанта, наведених в таблиці 2

Порівнюючи завдання для І та ІІ варіантів, наведених в стовпчиках А таблиць 1 і 2, можна побачити, що вони ідентичні, але розташовані в іншому порядку.

 

У табл. 3 наведені відповіді на завдання.

Таблиця 3

	Відповіді
Стовпчик А			Стовпчик Б
	І варіант (табл.1)
1			3
2			5
3			1
4			2
5			4
	ІІ варіант (табл.2)
1			3
2			4
3			5
4			1
5			2