Матеріали до уроків "Інтегруюча роль функціональної лінії при вивченні природничо-математичних дисциплін

Інтегруюча роль функціональної лінії

при вивченні природничо-математичних дисциплін

Есть тонкие властительные связи

Меж контуром и запахом цветка.

В. Я. Брюсов, «Сонет к форме»

Засвоєння змісту дисциплін природничо-математичного циклу може бути більш ефективним шляхом проведення інтегрованих уроків, взаємоорієнтації навчального змісту програм вчителями математики, фізики, хімії та біології. Зв’язки математики і природничих наук відбуваються у таких напрямках:

• деякі поняття з фізики, хімії та біології ілюструють закономірності, які вивчаються в математиці (закономірності у вигляді елементарних функцій досить поширені у природі);
• на уроках з природничих наук з’являється потреба в математиці (необхідність створити математичну модель, скористатися законами математики);
• у процесі вивчення фізики, хімії та біології здійснюється закріплення математичних знань.

Дана стаття присвячена функціональній лінії в курсі математики як засобу встановлення внутрішньопредметних  зв’язків, як «містка» між природничими шкільними дисциплінами.

Поняття функції виникло порівняно нещодавно – лише у XVII столітті: у зв’язку з географічними і астрономічними відкриттями, створенням машин і механізмів виникли умови для створення математики, яка б вивчала залежності величин, зокрема пов’язаних з рухом. Велике значення для цього мали ідеї французького філософа і математика Рене Декарта (1596 - 1650), який першим почав застосовувати букви для запису залежностей, зображати їх на координатній площині. Знадобилося менше ніж століття, щоб функції і пов’язані з ними задачі стали одними з найважливіших математичних об’єктів. В 1834 р. російський математик М. І. Лобачевський писав: «Не можна сумніватися ані в істинності того, що все в світі може бути представлено числом, ані в справедливості того, що всяка в ньому змінна та відношення виражається аналітичною функцією». Учені почали розробляти теорії дослідження окремих класів функцій, застосовувати їх до розв’язування багатьох прикладних задач. У сучасній математиці поняття функції є одним з найважливіших. Існує багато розділів математики, які займаються вивченням функцій та їх застосуванням до опису явищ і процесів.

Функція – це первинна математична модель, саме тому система знань учнів про функції, їх властивості та графіки, як в явній так і в неявній формі є стрижневою в шкільному курсі. Функціональний матеріал дає можливість розвивати всі пізнавальні процеси, розкривати загальнонаукову та загальнокультурну роль математики, здійснювати професійну орієнтацію учнів.

Наступна  задача демонструє учням необхідність «функціональних» знань для практичного застосування.

Задача (ілюструє зв’язок «алгебра-геометрія-будівництво»). Вікно має форму прямокутника завершеного аркою у формі півкруга. Діаметр півкруга дорівнює основі прямокутника. Периметр вікна дорівнює 2р. Якими мають бути розміри вікна, щоб крізь нього проходило найбільше світла.

 Розв’язання. Позначимо через х радіус півкруга, що утворює аркову частину вікна, через h – висоту прямокутної нижньої частини. Тоді 2p=2x+2h+πx, звідки h=p-x- πx. Площа вікна – функція аргумента х: S(х)=2x(p-x- πx)+ πx² або S(х)= - (2+ ) х² + 2px, 0˂x˂. Така квадратична функція набуває найбільшого значення при x₀=. Це значення функції дорівнює . При цьому значенні h =, тобто h= x₀.

Відповідь. Пропускна здатність вікна буде найбільшою, якщо радіус півкруга арки дорівнює висоті прямокутника і дорівнює .

В літературі  можна знайти безліч прикладів застосування того чи іншого виду функцій в природничих науках. Отже нескладно переконати учнів в затребуваності знань про класи функцій, їхніх властивостей в сучасному світі. Але, на жаль, потребує немалих зусиль для вчителя знайти змістовні, цікаві і доступні для школярів практичні завдання на застосування знань про елементарні функції. В ідеалі такі задачі повинні виконувати інтегруючу міжпредметну роль і в той самий час сприяти виробленню суто математичних навичок, а саме:

• читання графіків функцій (тобто встановлення за графіком їхніх властивостей і характеристик);
• побудова різними методами графіків функцій, заданих формулами;
• застосування властивостей функцій (монотонності, знакосталості, парності тощо);
• перетворення графіків функцій за заданими формулами і, навпаки, перехід від графічного способу задання функцій до формульного.

Розглянемо декілька таких корисних задач, що «працюють» на стику «алгебра-фізика». Використання завдань фізичного змісту при вивченні видів функцій на уроках алгебри згодом допоможе учням на уроках фізики природньо сприймати відповідні математичні моделі.

Лінійна функція. Деяка кількість газу займала при 20⁰ С об’єм 107 см³, при 40⁰ С об’єм став дорівнювати 114 см³.

1.                     Складіть, виходячи з закону Гей-Люссака, функцію, що виражає залежність    об’єму V газу від температури T.
2.                     Яким буде об’єм при 0⁰ С?
3.                     Побудуйте графік залежності об’єму V газу від температури T.

Квадратична функція. Чимало фізичних залежностей виражаються за допомогою квадратичної функції. До них належать залежність кінетичної енергії тіла від швидкості його руху, залежність електричної потужності від сили струму, залежність електростатичного поля від його напруженості тощо. Квадратична функція описує рух під час вільного падіння, падіння під кутом до горизонту, переміщення тіла при рівноприскореному русі.

Для допомоги у вивченні таких рухів на уроках фізики доцільно вже при відпрацюванні навичок побудови параболи запропонувати такі завдання.

Приклад. Під час вільного падіння тіла з початковою швидкістю v₀ залежність шляху від часу виражається формулою s = v₀t + , де s – шлях, м; t - час, с; g - прискорення вільного падіння. Побудуйте графік цієї залежності, якщо v₀ = 10 м/с.

Приклад. М’яч підкинуто вертикально вгору із землі зі швидкістю 30 м/с. Одночасно інший м’яч випущено з рук на висоті 100 м над місцем підкидання першого м’яча. На якій висоті і в який момент часу м’ячі вперше зустрінуться.

Розв’язання. Спрямовуємо вісь ординат вертикально вгору, а початок координат сумістимо з початком руху м’яча, підкинутого із землі. Для першого і другого м’ячів маємо відповідно закони зміни координат h₁(t) = 30t - 5t², h₂(t) = 100 – 5t² (для прискоренння вільного падіння приймемо округлення g≈10 м/с).   Перша «зустріч» м’ячів відбудеться в той момент часу t , коли h₁(t) = h₂(t). Маємо рівняння: 30t + 5t² =100 - 5t². Враховуючи, що t˃0, маємо що м’ячі вперше зустрінуться через 3с на висоті 44м.

Приклад. Кабіна ліфта піднімається протягом перших 4 с рівноприскорено, досягаючи швидкості 4 м/с. З цією швидкістю кабіна рухається протягом наступних 8 с, а останні 3 с вона рухається рівносповільнено.

1.                    Записати закон зміни її швидкості.
2.                    Записати закон зміни руху кабіни.
3.                    На якій висоті опиниться кабіна через 15 с?
4.                    Побудувати графік залежності швидкості від часу.
5.                    Побудувати графік закону руху кабіни.

Розв’язання. Спрямуємо вісь ординат вертикально вгору, а початок координат сумістимо з початком руху кабіни ліфта.

1.                    Розглянемо рух кабіни на трьох ділянках.

а) На проміжку часу [0;4] швидкість змінювалася лінійно за законом v(t) = at+b. За умовою маємо: v(0)=0, v(4)=4. Звідси a=1, b=0. Отже, v(t)=t, тобто прискорення руху на цьому проміжку часу дорівнювало 1 м/с².

б) На проміжку часу [4;12] швидкість була сталою і дорівнювала 4 м/с: v(t)=4.

в) Оскільки на проміжку часу [12;15] рух кабіни був рівносповільненим, то швидкість змінювалася лінійно. Нехай закон зміни швидкості мав вигляд v(t) = at+b. Відомо,що v(12)=4, v(15)=0. Звідси a=-, b=20. Відтак, v(t)= - t+20. Прискоренння на цьому проміжку часу дорівнювало а= - м/с². Отже,

   t, якщо 0 ≤ t ≤ 4,

   v(t) =   4, якщо 4 ≤ t ≤ 12,

   - t+20, якщо 12 ≤ t ≤ 15.

2) Закон рівнозмінного руху тіла має вигляд x = x₀ + v₀t + , де х₀ – початкова координата тіла (у момент часу t=0), v₀ – початкова швидкість, а – прискорення.

а) Оскільки на проміжку часу [0;4] рух був рівноприскореним з прискоренням а=1, х₀=0,    v₀=0, то х= . Зауважимо, що х(4)=8.

б) На проміжку часу [4;12] рух був рівномірним, х = k+ v₀t, v₀=4. Оскільки х(4)=8, то 8=k+4∙4, k= -8, х=4t – 8, х(12) = 40.

в) На проміжку часу [12;15] рух був рівносповільненим із прискоренням a = - , закон руху має вигляд x=x₀+v₀t - . Відомо, що в момент часу t=12:  х(12)=40. Якби кабіна рухалася за цим законом із самого початку, то із закону зміни швидкості            v(t)= - t+20 на цьому проміжку часу випливає, що v₀= v(0)=20. З того, що х(12)=40, робимо висновок: 40=х₀ + 20∙12 - ∙12².  Звідси х=-104, х(t) = -104+20t- Остаточно маємо:

   , якщо 0 ≤ t ≤ 4,

  х(t) =   4t-8, якщо 4 ≤ t ≤ 12,

   - , якщо 12 ≤ t ≤ 15.

3) Оскільки х(15) = -104+20∙15- = 46, то через 15 с кабіна ліфта опиниться на висоті 15 м. 

4) Графік швидкості зображено на рисунку 1

5) Графік закону руху зображено на рисунку 2

Відповідь. 1)    t, якщо 0 ≤ t ≤ 4,

     v(t)  =   4, якщо 4 ≤ t ≤ 12,

     - t+20, якщо 12 ≤ t ≤ 15;

  2)   , якщо 0 ≤ t ≤ 4,

     х(t) =   4t-8, якщо 4 ≤ t ≤ 12,

     - , якщо 12 ≤ t ≤ 15.

3.                    46 м/с;
4.                    рис. 1;
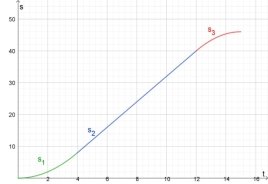5.                    рис. 2.

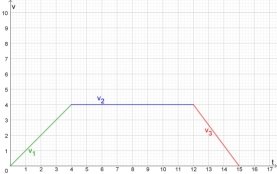
Рис.1. Графік закону швидкості   Рис.2. Графік закону руху

В задачі про ліфт учні стикаються не тільки з квадратичними, але й з вивченими раніше лінійними функціями. Закони зміни швидкості кабіни ліфта та зміни її руху описуються кусковими функціями, які в реальному житті часто є математичними моделями процесів.

Приклад. Рух тіла, кинутого під кутом до горизонту.

Траєкторіями метальних снарядів цікавилися філософ Арістотель (ІV ст.. до н.е.), геніальний самоук Ніколо Тарталья (ХVІ ст.). Але лише наприкінці ХVІ ст. Галілей встановил закони падіння тіл в параметричній формі:

x = v₀tcosα, y = v₀tsinα - . Визначити траєкторію руху тіла як функцію у(х).

Учні легко отримають , що y=xtg -/2v₀ ²cos²α і з’ясують, що траєкторія руху снаряду - парабола, вітки якої напрямлені униз. Тепер при певних значеннях параметрів v₀ і α можна знайти відстань, на яку відлетить снаряд, час його руху, найбільшу висоту, на яку він підніметься. Знаходження нуля функції х = означає знаходження точки падіння снаряду. Аналіз властивостей функції у = призводить до висновку, що нуль функції приймає найбільше значення при α = 45⁰  , тобто при нахилі зброї під кутом 45⁰ дальність враження буде найбільшою. Крім того, побудова графіка траєкторії при зміні того чи іншого параметра дасть можливість наочно порівняти результати обчислень.

У фізиці використовується проектування траєкторій рухів на осі прямокутної системи координат. Тому за наявності часу на уроці або в позакласній роботі можна ознайомити учнів з параметричним способом.

Параметричне рівняння траєкторії руху - це система функцій x = x(t) , y = y(t), a≤t≤b,що складається з рівнянь, які в кожний момент часу t₀ задають положення точки (x(t₀),y(t₀)) на координатній площині

Приклад. Визначити траєкторію руху тіла за допомогою параметричного рівняння x = 1 + 2t, y = 1 + 4t² , t≥0.

Шуканою траєкторією буде частина параболи y = (x-1)² + 1 при x≥1.

Дві наступні вправи для 10 класу є ланками в ланцюгу «фізика-алгебра-геометрія»

Приклад. Скласти параметричне рівняння руху кінця годинникової стрілки.

Протягом доби стрілка годинника описує коло , що задається рівнянням x²+y²=1. Враховуючи, що кут повороту φ рівномірно залежить від часу t (φ = ωt) параметричне рівняння кола можна записати через тригонометричні функції у вигляді:

 x = R cosωt, y= R sinωt, 0⁰ ≤ t≤ .

Приклад. Визначити траєкторію руху тіла за законом х = 3сos φ, y = 2sin φ + 1.

Cкориставшись тотожністю cos²φ + sin²φ = 1, отримаємо рівняння еліпса  + .

Цікавою для школярів буде така інформація про космос. Якщо початкова швидкість тіла при запуску з Землі дорівнює перший космічній швидкості – 7,9 км/с, то тіло рухається по коловій орбіті навколо Землі. Якщо початкова швидкість тіла при запуску з Землі перевищуватиме першу космічну швидкість, але не досягне другої , то тіло рухатиметься по еліптичній орбіті навколо Землі. Якщо початкова швидкість тіла при запуску з Землі дорівнює другій космічній швидкості – 11,2км/с , то тіло рухається по параболічній траєкторії, віддаляючись від Землі. Якщо початкова швидкість тіла при запуску з Землі перевищуватиме другу космічну швидкість, то тіло рухається по гіперболічній траєкторії.

Числові послідовності так само як і функції можна задавати формулами, таблицями, описовим способом, вони також мають характеристики монотонності (зростання, спадання, сталість), область визначення (множина натуральних чисел), обмеженість і необмеженість. Послідовності є функціями натурального аргумента. Формули n-го члена послідовності і суми перших n членів послідовності – формули функціональних залежностей, тобто a_n = a(n), S_n = S(n).

Так, при вивченні арифметичної прогресій зазначаємо наступне:

• член a_n арифметичної прогресії знаходиться у лінійній залежності від його номера: a_n = d∙n + (a₁ – d), де d – різниця прогресії;
• сума S_n перших n членів арифметичної прогресії знаходиться у квадратичній залежності від кількості членів: S_n = ∙n² + (a₁ – )∙n.

Оскільки на момент вивчення геометричних прогресій показникова функція ще не знайома учням, функціональну природу геометричної прогресії можна обговорити вже в 11 класі на вступному уроці з теми «Показникова функція», коли пояснюється актуальність знань про таку функцію на прикладах з різних сфер людської діяльності.

Ріст народонаселення. Зміна числа жителів країни за невеликий відрізок часу описується формулою N=N₀∙e^at , де N₀ - число людей в момент часу t=0,  N – число людей в момент часу t,  a –стала.

Взагалі закон органічного росту в біології записують показниковою функцією у=у₀∙e^at.

Зміна атмосферного тиску. Атмосферний тиск змінюється  в залежності від висоти h над рівнем моря за законом p = p₀ a^h ,де p ₀ ─ атмосферний тиск над  рівнем моря; a ─ постійна величина.

Радіоактивний розпад. Під час радіоактивного розпаду маса m речовини змінюється протягом часу t за законому: m =m₀ a^kx , де m ─  маса речовини через t років після початку розпаду; m₀ ─ початкова маса речовини; k и a  ─  постійні величини для даної речовини.

Для відпрацювання навичок побудови графіка показникової функції зручними буде такі завдання.

Приклад. Нехай з початку спостережень маса колонії бактерій дорівнювала 1г, причому за кожну наступну годину вона зростала в 2 рази. Побудувати графік зміни маси m в залежності від часу t.

Згадуючи формулу n-го члена геометричної прогресії встановлюємо, що залежність між масою і часом виражається формулою m=2^t. Для побудови графіка обчислимо масу колонії (y) через 1, 2, години (x) до початку і після початку спостереження. Дані обчислювання занесемо в таблицю, вважаючи, що час до початку спостереження був відємним.

Будуємо графік.

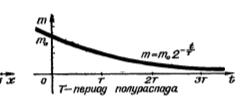
Приклад. Зміна маси радіоактивної речовини відбувається за формулою

m = M∙( , де М – маса речовини в початковий момент часу t=0, m – маса речовини в момент часу t, T – період напіврозпаду речовини (проміжок часу, протягом якого вихідна кількість речовини зменшилася двічі). Період напіврозпаду йоду Т = 8 діб. Побудуйте графік радіоактивного розпаду йоду та визначте, якою стане його маса через 40 діб, якщо його початкова маса 200 г.

Графік буде задаватися формулою у=200∙( . Через 40 діб маса йоду стане 6,25г.

Старшокласникам буде цікавим дізнатися про застосування в природничих процесах логарифмічної функції:

1.                     психофізичними дослідами установлено, що величина відчуттів змінюється повільніше ніж сила подразника. Інтенсивність відчуттів Е виражається логарифмічною залежністю  Е = К• lgJ +С, де J – інтенсивність подразника; K и С – деякі сталі, що задаються даною сенсорною системою (закон Вебера – Фехнера).
2.                     якщо літак буде летіти, дотримуючись весь час одного курсу, тобто перетинаючи всі меридіани під одним і тим самим кутом, то його шлях зобразиться на карті логарифмічною спіраллю.

Аналогічних прикладів існує безліч, але в навчальному процесі необхідно мати не перелік таких застосувань, а й завдання, які б давали уявлення про актуальність в сьогоденній науці таких функціональних залежностей.

Прикладом геометричної прогресії може бути ряд чисел, що обчислюються за формулою складних відсотків.

Приклад. На деякій лісовій ділянці на даний момент часу можна заготовити 4∙10⁵ м³ деревини. Щорічний приріст деревини дорівнює 4 %. Скільки деревини можна буде заготувати на цій ділянці через 5 років.

За формулою  A_n = A₀∙(1 + )ⁿ , де n – кілкість років, A₀ – початковий об’єм деревини, p –  відсоток щорічного приросту деревини, знаходимо , що через 5 років буде

А = 4∙10⁵∙(1 + )⁵ ≈ 4,86∙10⁵ м³ деревини, що на 86000 м³ більше.

Отже, поєднання тем зі споріднених природничо-математичних дисциплін за допомогою поняття «функція», їх природнє взаємопроникнення дає змогу формувати в учнів науковий світогляд, забезпечуючи повноцінний характер і суспільно необхідний рівень освіти.