Урок "Функція. Область визначення та значень"

Конспект уроку з алгебри для 9 класу

Уроку 1: «Функція. Область визначення, область значень, графік функції.»

Мета уроку:

навчальна: повторення  та закріплення знань про функції та їх графіки, отриманих у 7-8 класах,

розвивальна: формувати  уявлення про ідеї і методи графічного відображення залежних величин  та її роль у пізнанні навколишнього світу; розвивати  алгоритмічне мислення учнів, логічне мислення, просторову уяву, наочно-дійове мислення учнів;

виховна: виховувати: алгоритмічну культуру, звичку до системної розумової справи, інформаційну культуру.

Форма проведення заняття: урок

Тип уроку:  формування  знань та вмінь щодо властивостей функцій.

Обладнання: комп’ютер, презентація, підручники.

План уроку:

I. Організаційний етап

Підготовка учнів до роботи на уроці. Створення позитивного настрою учнів. Побажання учням «Не просто слухати, а чути. Не просто дивитися, а бачити. Не просто відповідати, а міркувати. Дружно і плідно працювати.»

II. Формування мети й завдань уроку

Учитель: Сьогодні ми з вами пригадаємо теоретичний та практичний матеріал щодо функцій та їх графіків, які ви вивчали у 7 та 8 класі. Визначимо практичну значущість цих знань у житті та навчимося застосовувати свої вміння, які ви отримали у 8 класі для визначення деяких властивостей функції.  Тому саме, тема сьогоднішнього уроку : “ Функція. Область визначення, область значень, графік функції. ”

III. Мотивація навчальної діяльності

Форма: фронтальна

Метод: пояснювально-ілюстративний, повідомлення учням теоретичної значущості навчального матеріалу.

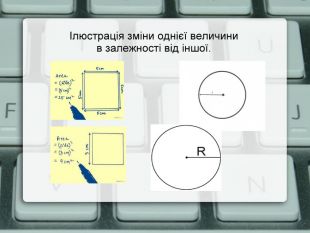
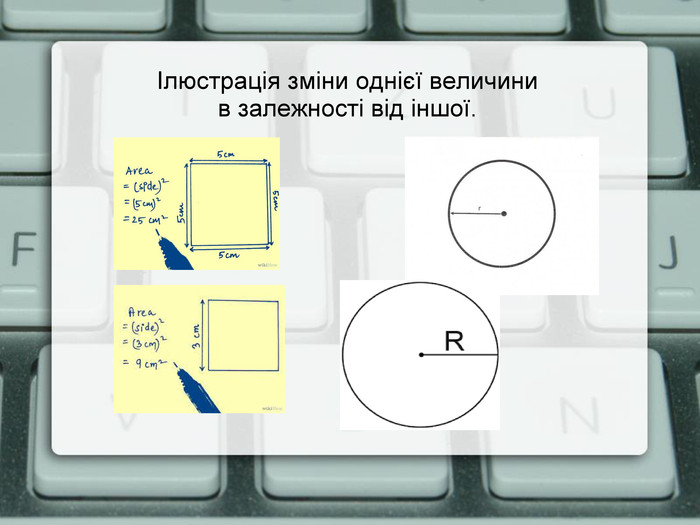
Учитель: При вивчені явищ оточуючого світу та в практичній діяльності   виникає потреба розглядати величини різної природи: довжину, площу, ооб’єм, масу, температуру, час тощо. В залежності від умов, які розглядаються, деякі з величин є постійними, інші змінюються. Наприклад, при зміні обсягу продажу напою Coca-Cola змінюється прибуток магазину, що його реалізує на продаж; або при зміні площі вашої кімнати змінюється кількість шпалер, які потрібні на її оздоблення; або  при зміні сторони квадрата, змінюються його периметр, і таких прикладів можна навести багато. (слайд 2) Запропонуйте, будь-ласка, свої приклади. ( Учні наводять декілька своїх прикладів)

Отже, всі наведені приклади можна описати за допомогою математики. Математичною реалізацією  взаємозв’язку реальних величин є ідея функціональної залежності, функції – яке являється одним  ключових понять математики.

IV. Актуалізація опорних знань, умінь, навичок.

 Інтелектуальна розминка за питаннями.

 1.Що ми називаємо координатною площиною?  (дві взаємоперпендикулярні координатні прямі: абсциса та ордината. Координатна площина розбиваю площину на чотири чверті).

2. Координати точки на площині? (кожній точці у відповідність ставиться пара чисел: абсциса і ордината).

3. Як визначити  координати точки? (побудувати проекцію на ось OX та OY для відповідної точки).

4. Які елементарні функції ви вивчали у попередніх класах?

V. Вивчення нового матеріалу: теорія, практика.

Метод: пояснювально-ілюстративний, формування понять, розв’язання практичних задач.

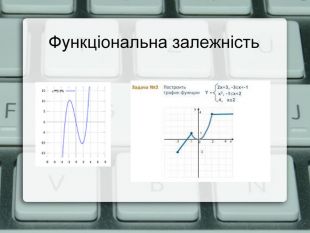
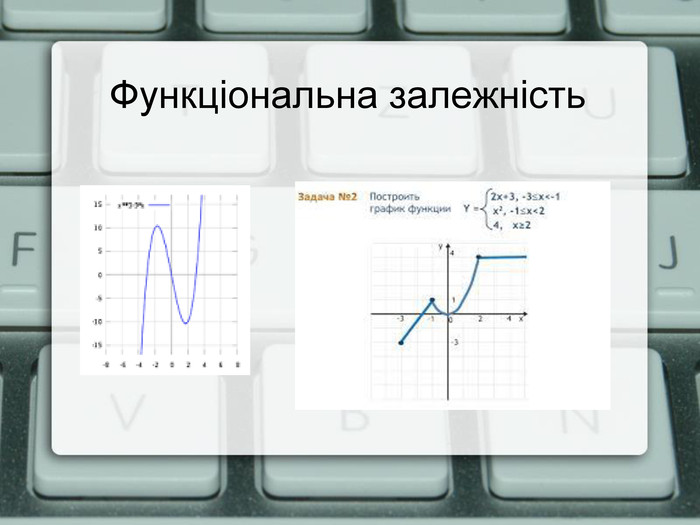
Учитель: Нехай маємо деяку величину, яка змінюється незалежно від іншої, наприклад, ваш вік, і позначимо її через Х. Тоді існує інша величина, наприклад, ваш зріст,  позначимо її Y, яка змінюються в залежності від  першої Х. Причому кожному значенню Х відповідає  єдине значення Y. Така залежність записується як  y(x)  або y=f(x).  Змінну х називають незалежною або аргументом , змінну y -  залежною або функцією. Залежність коли аргументу відповідає тільки одна значення функції називається функціональною. Наприклад слайд (3), якщо ж розглянемо залежність як на слайді 4, то можемо побачити що така залежність не є функціональною, так як одному значенню аргументу відповідає декілька значень функції. (слайд 4)

Існує декілька способів представлення функції. Розглянемо їх:

1. Функція представлена формулою (аналітичне). При цьому функція може бути задана однієї формулою  на всій області визначення або декількома для різних частин області визначення . (слайд 3)
2. Табличне представлення.  Табличний спосіб використовується  для запису показників досліджень, коли використовується залежність між величинами.(слайд 5)
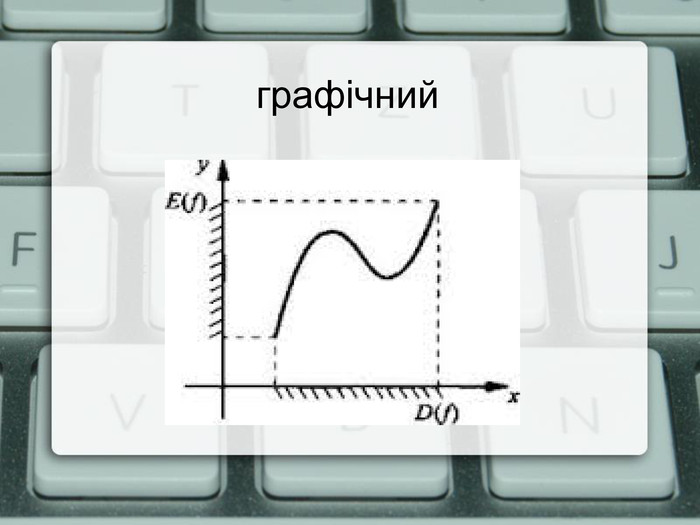
3. Функція може буди задана графіком. Графічний метод широко використовується в наукових дослідженнях  та на сучасному виробництві.(слайд 3 або 6)

Крім цих основних форм функція також може бути задана  описовим методом, наприклад y=[x], де [x] — ціла частина від х  (Слайд 7)

Згадаємо деякі характеристика функції:

Означення 1. Областю визначення функції називають множину аргументу  х для яких визначена величина y(x) - функція.

Позначають D(y): х є ... або  D(f): х є .....

Означення 2 Областю значень функції називають множину значень, яку приймає змінна y, тобто функція  і позначають E(y): y  є.... E(f): y є...

Загадємо функції та їх графіки, які вивчали у 7-8 класах. Розглянемо табличку, що знаходиться на стор 60 нашого підручника [1] (Слайд 8) (учитель разом з учнями вивчає табличку а потім на слайді називає кожну функцію відповідно до графіка)

VI. Первинне закріплення і корекція

Розв’язування задач за підручником [1]на стор. 61-62

№№ 7.3,  7.6, 7.8 (І ст.)

VII. Етап перевірки первинного розуміння

Розв’зання задач на дошці

підручник [1]: стор.62

№№ 7.8 (ІІ ст.) , 7.10, 7.15

додаткові завдання: (слайд 9)

• Знайти область визначення функції

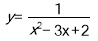
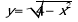
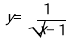
VIII. Підведення підсумків уроку

Метод: опитування постановка питань учнями один одному

IX. Повідомлення домашнього завдання  та оцінок за урок

 § 7 стор. 59 №№ 7.7;   7.9;   7.18 (слайд 9)

 Використана література:

1. Мерзляк А.Г., Полонський В.Б., Якир М.С. АЛГЕБРА, Харьків “Гімназія”, 2017.
2. Богатырев Г.И., Боковиев  О.А. Математика для подготовительных курсов техникумов, 1988