Матеріали до уроку "Перетворення у просторі"

Перетворення у просторі: симетрія відносно точки, симетрія відносно площини, паралельне перенесення, подібність

1. Перетворення фігур. Рух. Рівність фігур

Рухом називають перетворення, при якому зберігаються відстані між точками.

Властивості руху. Точки, які лежать на прямій переходять у точки, які лежать на прямій і зберігається порядок їх взаємного розміщення.

Звідси при рухах: пряма переходить у пряму, промінь – у промінь, відрізок у відрізок, що дорівнює даному, кут – у кут, що дорівнює даному, площина – у площину.

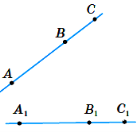
Дві фігури називають рівними, якщо існує рух, який відображає одну з них на іншу.

2. Симетрія відносно точки

Точки A і A₁ називають симетричними відносно точки O, якщо O – середина відрізка AA₁. Перетворення, при якому кожна точка даної фігури відображається на точку, симетричну їй відносно O, називають симетрією відносно точки O.

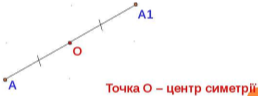
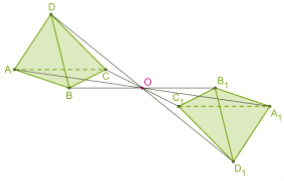
Якщо симетрія відносно деякої точки O відображає дану фігуру на ту саму фігуру, таку фігуру називають центрально-симетричною, а точку O – її центром симетрії.

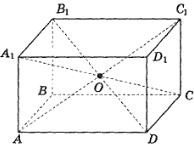
3. Симетрія відносно площини

Точки A і A₁ називають симетричними відносно площини, якщо ця площина перпендикулярна до відрізка AA₁ і ділить його навпіл. Перетворення, яке відображає кожну точку фігури на точку, симетричну їй відносно даної площини, називають симетрією відносно площини.

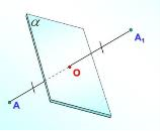
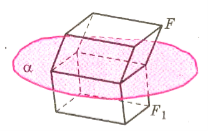
Якщо деяка фігура симетрією відносно площини α відображається на себе, цю фігуру називають симетричною відносно площини, а α – площиною симетрії даної фігури.

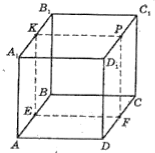
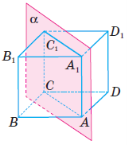
Точки, симетричні точці A(х; у; z) відносно початку координат і координатних площин, мають такі координати:

відносно точки О(0; 0; 0):  (-х; -у; -z);

відносно площини ху:  (х; у; -z);

відносно площини хz:  (х; -у; z);

відносно площини уz:  (-х; у; z).

4. Паралельне перенесення

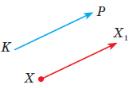
Нехай – який-небудь вектор, а X – довільна точка простору. Якщо точка X₁ така, що , то говорять, що паралельне перенесення на вектор  відображає точку X на X₁.

У результаті паралельного перенесення всі точки даної фігури переносяться в одному напрямі на однакові відстані.

Формули паралельного перенесення простору на вектор (a; b; c), при якому точка A(x; y; z)

переходить у точку A′(x′; y′; z′):

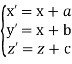
5. Перетворення подібності

Перетворення фігури F, при якому відстані між її точками змінюються в одну й ту саму кількість разів, називають перетворенням подібності фігури F.

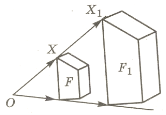
6. Гомотетія

Якщо точки O, X і X₁ є такими, що , де k ≠ 0, то говорять, що точка X₁ – образ точки X при гомотетії із центром O та коефіцієнтом k.

Приклади

1. Задано точку А(-1; 2; 3). Знайти координати точки, симетричної точці А відносно площини ху.

Розв'язання. Симетрична точка відносно площини не змінює координат, які належать площині тобто x, y не міняємо. Координата по осі z змінює знак на протилежний.
A₁(-1; 2; -3).

2. Дано точка А(3; 5; 2). Знайти точки, симетричні даній відносно координатних площин і початку координат.
Відповідь: точка, симетрична точці А відносно площини ху, А₁(3; 5; -2);

відносно площини yz – А₂(-3; 5; 2);

відносно площини xz – А₃(3; -5; 2);

відносно початку координат – А₄(-3; -5; -2).

3. Точки А(5; -3; 4) та В(-3; 1; -2) симетричні відносно точки С. Знайти координати точки С.

Розв’язання. За означенням симетрії відносно точки С – середина відрізка АВ. Тоді

;  ;  ;

;  ;  ;

С(1; -1; 1).

4. Паралельне перенесення задано формулами х₁ = х – 4; у₁ = у + 2; z₁ = z – 6.

1) У яку точку перейде точка М(4; -2; 7)?

2) Яка точка переходить у точку К₁(-2; 0; -1)?

Розв’язання.

1) Знайдемо координати точки М₁, підставивши у формули паралельного перенесення координати точки М. Тоді х₁ = 4 – 4 = 0;  у₁ = -2 + 2 = 0;  z₁ = 7 – 6 = 1;

М₁(0; 0; 1)

2) Щоб знайти координати точки К, підставимо у формули паралельного перенесення координати точки К₁. Маємо

-2 = х – 4;  х = 2;

0 = у + 2;  у = -2;

-1 = z – 6;  z = 5;

К(2; -2; 5)

5. Трикутник АВС гомотетичний трикутнику А₁В₁С₁ відносно початку координат з коефіцієнтом гомотетії k = 2. Знайдіть координати вер­шин трикутника А₁В₁С₁, якщо А(1; 0; 0), В(0; 3; 0), С(0; 0; -3).

Розв’язання. За означенням гомотетії , , , де точка О(0; 0; 0) – центр гомотетії.

Координати векторів (1; 0; 0), (0; 3; 0), (0; 0; -3), тоді , тобто (2; 0; 0). Аналогічно (0; 6; 0), (0; 0; -6). Отже, А₁(2; 0; 0), В₁(0; 6; 0), С₁(0; 0; -6).