Матеріали до уроку: " Розв’язування систем лінійних рівнянь з двома змінними способом додавання "

Практична робота № 4.

Тема. Розв’язування систем лінійних рівнянь з двома змінними  способом додавання

Мета: формування вмінь розв’язувати  системи лінійних рівнянь з двома змінними  способом додавання. 

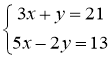Завдання. Розв’язати систему лінійних рівнянь з двома змінними  способом додавання: 

Хід роботи:

1. Помнож перше рівняння на 2, щоб коефіцієнти при змінній у стали протилежними числами.
2. Додай почленно ліві і праві частини рівнянь системи.
3. Розв’яжи утворене рівняння з однією змінною х.
4. Підстав знайдене значення х  в перше початкове рівняння і знайди відповідне значення у.
5. Переконайся, що отримані значення є коренями кожного з рівнянь.
6. Зроби висновок щодо отриманих значень.
7. Запиши відповідь.

Очікуваний результат