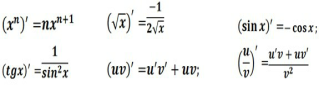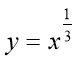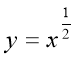МЕТОДИ І ПРИЙОМИ РОЗВИТКУ КРИТИЧНОГО МИСЛЕННЯ НА УРОКАХ МАТЕМАТИКИ

Про матеріал

Робота містить аналіз теоретичного матеріалу щодо важливості формування компетентностей учнів шляхом використання технології розвитку критичного мислення на уроках математики, висвітлено питання організації і методики технології розвитку критичного мислення, описано структурні елементи базової моделі уроку, розглянуто методи та прийоми формування критичного мислення. У роботі доводиться доцільність використання технології розвитку критичного мислення на уроках математики, розкрита важливість формування у здобувачів освіти математичної компетентності, обґрунтовується необхідність створення таких умов, які забезпечують активізацію освітнього процесу, сприяють формуванню системи знань з математики. Практична реалізація досвіду довела, що застосування технології розвитку критичного мислення дозволяє домагатися таких освітніх результатів як уміння працювати зі зростаючим і постійно оновлюваним інформаційним потоком в різних областях знань; вміння висловлювати свої думки; вміння виробляти власну думку на основі осмислення різного досвіду, ідей і уявлень; вміння вирішувати проблеми; здатність самостійно займатися своїм навчанням; вміння співпрацювати і працювати в групі; здатність вибудовувати конструктивні взаємини з іншими людьми.

Перегляд файлу

Київський університет імені Бориса Грінченка

Інститут післядипломної педагогічної освіти

Тема досвіду роботи

МЕТОДИ І ПРИЙОМИ РОЗВИТКУ КРИТИЧНОГО МИСЛЕННЯ

НА УРОКАХ МАТЕМАТИКИ

Кухаревич Варвара Омелянівна

вчитель математики

вищої квалафікаційної категорії

старий вчитель

спеціалізованої школи №196

міста Києва

Київ- 2022

ПЕРСОНАЛІЯ АВТОРА

1. Прізвище, ім’я, по-батькові: Кухаревич Варвара Омелянівна

2. Освіта: Вища

3.Повна назва вищого навчального закладу, що закінчив: Ужгородський державний університет

4. Рік закінчення вищого навчального закладу: 1986

5. Спеціальність за дипломом: математик. Викладач

6. Посада: вчитель математики

7. Місце роботи: спеціалізована школа №196

8. Робоча адреса: 03194, м. Київ, вулиця Зодчих, 22, 405-40-22

9. Педагогічний стаж: 36 років

10. Звання: старший вчитель

11. Кваліфікаційна категорія: вища

12. Проблеми, над розв’язанням яких працює: «Методи і прийоми розвитку критичного мислення на уроках математики»

13. Наявність друкованих робіт – публікації на національній всеосвітній платформі «Всеосвіта» і освітньому проекті «На Урок»

14. Нагороди:

Грамота: Відділ освіти Кременецької районної державної адміністрації

«за багаторічну сумлінну і творчу працю на ниві навчання і виховання підростаючого покоління, високий професіоналізм та з нагоди дня працівника освіти», 2014 р, 2016 р.

Грамота:

Департамент освіти і науки Тернопільської обласної державної адміністрації

Тернопільська обласна організація Профспілки працівників освіти і науки України

«за багаторічну сумлінну і творчу працю на ниві навчання і виховання підростаючого покоління, високий професіоналізм та з нагоди дня працівника освіти», 2013р.

Грамота: Кременецька районна державна адміністрація

Кременецька районна рада

«за багаторічну сумлінну, творчу працю на ниві навчання і виховання підростаючого покоління, високий професіоналізм та з нагоди дня Працівника освіти», 2015р.

Подяка: Відділ освіти Кременецької районної державної адміністрації

Кременецька районна рада

«за сумлінну і творчу працю на ниві навчання і виховання підростаючого покоління та з нагоди Дня працівника освіти» ,2015р, 2016р

АНОТАЦІЯ

Кухаревич Варвара Омелянівна,

учитель математики спеціалізованої школи №196

Святошинського району міста Києва,

учитель вищої кваліфікаційної категорії, старший учитель

Авторська методика викладання предмета

«МЕТОДИ І ПРИЙОМИ РОЗВИТКУ КРИТИЧНОГО МИСЛЕННЯ

НА УРОКАХ МАТЕМАТИКИ»

У роботі доводиться доцільність використання технології розвитку критичного мислення на уроках математики, розкрита важливість формування у здобувачів освіти математичної компетентності, обґрунтовується необхідність створення таких умов, які забезпечують активізацію освітнього процесу, сприяють формуванню системи знань з математики.

Практична реалізація досвіду довела, що застосування технології розвитку критичного мислення дозволяє домагатися таких освітніх результатів як уміння працювати зі зростаючим і постійно оновлюваним інформаційним потоком в різних областях знань; вміння висловлювати свої думки; вміння виробляти власну думку на основі осмислення різного досвіду, ідей і уявлень; вміння вирішувати проблеми; здатність самостійно займатися своїм навчанням; вміння співпрацювати і працювати в групі; здатність вибудовувати конструктивні взаємини з іншими людьми.

ЗМІСТ

ВСТУП	……………………………………………………………	5
ОРГАНІЗАЦІЯ НАВЧАННЯ ЗА ТЕХНОЛОГІЄЮ РОЗВИТКУ КРИТИЧНОГО МИСЛЕННЯ……………..………………………….….		7
1.1.	Основні положення технології розвитку критичного мислення …………………………………………………	7
1.2.	Структура уроку за технологією розвитку критичного мислення……………………………………	10
1.3.	Методи навчання математики в структурі уроків критичного мислення……………………………………	12
МЕТОДИ І ПРИЙОМИ КРИТИЧНОГО МИСЛЕННЯ В ПРОЦЕСІ РОЗВИТКУ КРИТИЧНОГО МИСЛЕННЯ ……………………………….		15
2.1.	Характеристика методів та прийомів технології розвитку критичного мислення ………………………………..………..	15
2.2.	Організації навчальної діяльності учнів на уроках математики з використанням технології розвитку критичного мислення……………………………………..….	21
ВИСНОВКИ……………………………………………………………….		44
ДОДАТКИ………………………………………………………….		46
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ …..……………………………		53

ВСТУП

Суспільство потребує громадянина, який здатний до самоосвіти та самовдосконалення, вміє критично мислити, опрацьовувати різноманітну інформацію, використовувати набуті знання і вміння для творчого розв’язання проблеми, прагне змінити на краще своє життя і життя своєї країни. Саме на досягнення кінцевого результату, розвитку особистості через призму формування життєво необхідних компетентностей, націлена сучасна модель освіти.

Формування компетентності учнів здійснюється не тільки шляхом реалізації відповідного змісту освіти, але і вибором методів та технологій навчання. Необхідно, щоб у процесі навчання формувався новий тип мислення, новий стиль діяльності, орієнтований на більш ефективне вирішення проблем. Однією з найрезультативніших технологій є технологія розвитку критичного мислення.. Освітня технологія розвитку критичного мислення в процесі навчання – це сукупність різноманітність педагогічних прийомів, які спонукають учнів до дослідницької творчої активності, створюють умови для усвідомлення ними матеріалу, узагальнення одержаних знань.

З педагогічної точки зору критичне мислення – це комплекс мисленнєвих операцій, що характеризується здатністю людини: аналізувати, порівнювати, синтезувати, оцінювати інформацію з будь-яких джерел; бачити проблеми, ставити запитання; висувати гіпотези та оцінювати альтернативи; робити свідомий вибір, приймати рішення та обґрунтовувати його.

На уроках математики критичне мислення формується та розвивається під час опрацювання інформації, розв’язування задач, розв’язання проблем, оцінювання ситуації, вибору раціональних способів діяльності. Основними цінностями навчання математики, орієнтованого на використання прийомів технології розвитку критичного мислення, стають якісні знання, самостійне критичне мислення, вміння працювати з інформацією, приймати ціннісне аргументоване рішення і нести за нього відповідальність.

Актуальність дослідження можливостей використання технології розвитку критичного мислення зумовлена у необхідності формування математичних компетентностей учнів, пошуку методів, прийомів і форм навчання, створення на уроках математики умов для саморозвитку та самореалізації учнів через системне включення їх до різних видів активної навчально-пізнавальної діяльності. розвитку аналітичного підходу до будь-якого матеріалу, підвищення мотивації до отримання знань.

Мета роботи – дослідити можливості використання технології розвитку критичного мислення під час навчання математики і показати особливості її реалізації. Завдання роботи:

1.на базі теоретичного дослідження технології розвитку критичного мислення, спеціальної структури уроків, на яких використовуються елементи даної технології з’ясувати особливості використання даної технології на уроках математики;

2.визначити найбільш ефективні методи і прийоми технології критичного мислення у викладанні математики;

3.опрацювати варіанти організації навчальної діяльності здобувачів освіти та виявити прийоми і методи роботи, які забезпечують формування критичного мислення на уроках математики;

4. проаналізувати доцільність візуального структурування навчального матеріалу, що уможливлює апробувати навички і застосувати запропонований інструментарій на уроках математики.

Об’єктом дослідження є система методів, прийомів і форм навчання математики, а предметом – застосування прийомів навчальної діяльності ефективного навчання математики з використанням технології розвитку критичного мислення.

Методами дослідження є теоретичний аналіз матеріалів проекту Програми АНКМ («Активне навчання, критичне мислення») «Розвиток критичного мислення через читання та письмо» (РКМЧЧП), розробленою Джіні Стіл, Чарльзом Темплом, Куртом Мередітом і Скоттом Вальтером [2].

Практичне значення роботи полягає у тому, що її результати можуть бути реалізовані при розробці та проведенні уроків з математики вчителями загальноосвітніх закладів з метою підвищення рівня засвоєння навчального матеріалу, кращому формуванню вмінь учнів застосовувати знання на практиці.

РОЗДІЛ 1. ОРГАНІЗАЦІЯ НАВЧАННЯ ЗА ТЕХНОЛОГІЄЮ РОЗВИТКУ КРИТИЧНОГО МИСЛЕННЯ

Основні положення технології розвитку критичного мислення

Технологія «Розвиток критичного мислення» – універсальна, міжпредметна, дозволяє здобути такі освітні результати, як уміння працювати в різних галузях знань, уміння висловлювати свою думку усно чи письмово, уміння формувати особисту точку зору на підставі різноманітних ідей та уявлень, вміння працювати в групі.

У зарубіжній психолого-педагогічній думці теорію розвитку критичного мислення у своїх наукових працях використовували та досліджували Дж. Брунер, Д. Дьюї, Д. Клустер, А. Кроуфорд, М. Ліпман, Д.Макінстер, С.Метьюз, Р.Пауль, Ж.Піаже, В.Саул, Д.Халперн, Л.Виготський, О. Бутенко, С. Заїр-Бек, та інші вчені, в посібниках яких вміщено опис практичних підходів і дидактичні матеріали щодо впровадження методів і прийомів розвитку критичного мислення учнів у процесі викладання різних предметів у школі. Річард Пауль (США, 1993) запропонував роз'яснення критичного мислення як мислення про мислення, коли індивід міркує, щоб поліпшити своє мислення, що є однією з прийнятних до роз'яснення в педагогічній практиці. Видатному американському мислителю Д.Дьюї належить твердження, що фундаментальна мета сучасної освіти полягає не в наданні учням інформації, а в тому, щоб розвивати в них критичний спосіб мислення [13]. На думку відомого фахівця з цієї проблеми М.Ліпмана, критичне мислення є «вміле відповідальне мислення, що дозволяє людині формулювати надійні вірогідні судження, оскільки воно: а) засновується на певних критеріях; б) є таким, що самокоректується; в) випливає з конкретного контексту» [3].

У контексті наведеної мотивації розвитку критичного мислення у людини наприкінці XX ст. в США вчені та викладачі Джіні Стіл, Чарльз Темпл, Курт Мередіт і Скотт Вальтер опрацювали як інтерактивну форму навчальну технологію «Розвиток критичного мислення через читання та письмо» (Critical thinkin) (РКМЧП) [7]. Як стверджують дослідники, критичне мислення є «складним процесом творчої інтеграції ідей та джерел, переоцінки та перебудови понять та інформації. Воно є активним та інтерактивним процесом пізнання, що відбувається водночас на багатьох рівнях» [11].

Українські науковці Л.Велитченко, Г.Липкіна, С.Максименко, Л.Рибак, Н.Чернега та ін. вивчають шляхи формування в учнів критичності мислення й ознаки такого мислення як психологічного утворення. Питання організації навчання з метою розвитку критичного мислення учнів значною мірою розроблено вченими й дослідниками О.І.Пометун, Д.Л.Десятовим, К.О.Бахановим, І.І.Бондарук, О.В.Тягло, С.Терно. У працях О. Пометун подано характеристику розвитку критичного мислення як однієї із сучасних технологій навчання, що тісно пов’язана з інтерактивним навчанням. Деякі елементи теорії та практики розвитку критичного мислення в учнів основної школи можна запозичити в працях фахівців з методики навчання математики, вчителів-практиків.

Мета даної освітньої технології – розвиток інтелектуальних умінь учнів, необхідних не тільки в навчанні, а й у звичайному житті (вміння приймати зважені рішення, працювати з інформацією, аналізувати різні сторони явищ і ін.).

Цілі та завдання технології розвитку критичного мислення

1.Формування пізнавального інтересу в учнів та розуміння мети вивчення даної теми (питання, проблеми).

2.Розвиток внутрішньої мотивації до цілеспрямованого навчання.

3.Підтримання пізнавальної активності учнів.

4.Спонукання учнів до порівняння отриманої інформації з особистим досвідом і на її ґрунті формування аналітичного судження.

5.Розвиток критичного способу мислення.

6.Формування комунікативних навичок та відповідальності за якість власних знань.

Критичне мислення є складним процесом, який починається з ознайомлення з інформацією, а завершується прийняттям певного рішення та складається з кількох послідовних етапів:

сприйняття інформації з різних джерел;
аналіз різних точок зору, обрання своєї точки зору;
зіставлення з іншими точками зору;
добір аргументів на підтримку обраної позиції;
ухвалення рішення на основі доказів.

Технологія розвитку критичного мислення допомагає сформувати навички самостійного прийняття рішення (від чого відмовитися, а що взяти на озброєння), навички самоконтролю, самоорганізації, самоактуалізації, інформаційно-пізнавальної самостійності учнів.

Мета використання технології – навчити такого сприйняття навчального матеріалу, в процесі якого інформацію, що отримує учень, можна розуміти, сприймати, порівняти з особистим досвідом і на її ґрунті формувати своє аналітичне судження.

Розвиток критичного мислення можливий за виконання наступних умов:

учителем: прийняття різних ідей і думок; підтримка активності учнів у процесі навчання; підтримка впевненості учнів у тому, що вони не ризикують бути незрозумілими; віра в кожного учня;
учнями: розвиток впевненості в собі і розуміння цінності своїх ідей та думок; активна участь у навчальному процесі; повага до різних думок.

Виділено шість ключових елементів критичного мислення:

уміння мислити;
відповідальність;
формулювання самостійних суджень;
критерії, до яких апелює, на які спирається критичне мислення;
самокорекція;

уваги та чуйності до контексту.

Отже, суть і мета застосування технології розвитку критичного мислення така: освіта не дається вчителем (учителями), вона одержується самим учнем. Для цього вчитель має сам оволодіти новим мисленням, відповідним чином сприймаючи зміст програмового матеріалу, вибирати й застосовувати саме ті методи й прийоми навчання, які сприятимуть розвиткові критичного мислення. Стратегічним напрямом розвитку в учнів критичного мислення є навчання задавати запитання. Питання можуть бути уточнюючого характеру, проблемні, дослідницькі та питання-роздуми. Педагог має створити атмосферу схвалення розмаїття поглядів та думок, активізації пізнавальної діяльності, пошуку нестандартних шляхів розв’язання проблем, не повинен поспішати з висновками, натомість має спрямовувати процес дискусії на вирішення даної проблеми, заохочувати учасників до висловлювання власних думок.

Структура уроку за технологією розвитку критичного мислення

Система розвитку критичного мислення передбачає особливу структуру уроку: у кожному уроці є три фази – актуалізація (передбачення), побудова (конструювання) знань та консолідація (А.Кроуфорд, В.Саул, С.Метью, Д.Макінстер [2]).

Фаза актуалізації: під час уроку якої педагог спрямовує учнів на те, щоб вони думали над темою, яку починають вивчати, і ставили запитання.

Фаза актуалізації має на меті:

актуалізувати («оживити») в пам’яті учнів уже наявні знання;
неформальним шляхом оцінити те, що вони вже знають (у тому числі їхні помилкові уявлення чи ідеї);
встановити мету навчання;
зосередити увагу учнів на темі;
представити контекст для того, щоб вони зрозуміли нові ідеї.

На цьому етапі вчитель вирішує три завдання.

1.Пробудити, викликати зацікавлення, схвилювати, спровокувати учнів думати, згадувати те, що вони знають (для цього він спирається на набуті знання та досвід учнів, пропонує згадати, що їм відомо з даної теми, проаналізувати свої знання, спрямувати мислення у відповідне русло. Це дозволяє вчителю окреслити рівень та коло знань учнів, які згодом поповняться новими; відкоригувати помилки мислення).

2.Актуалізувати мислення учнів, пам'ятаючи, що навчання — це активна діяльність (учні мають усвідомити своє мислення у своїх словах через письмо або мовлення. Використовуючи різноманітні методи, форми та прийоми, вчитель активізує участь учнів у навчальному процесі, провокуючи їх до цілеспрямованого мислення, демонстрування вже набутих знань, висловлювання особистих думок, вибору форм навчання, мотивації інтересу до даної теми, критичного сприйняття нової інформації, усвідомлення здатності до саморозвитку та самоактуалізації).

3.Визначає мету та завдання навчання, формує інтерес учнів і розуміння мети вивчення даної теми (питання, проблеми), розвиває внутрішню мотивацію до цілеспрямованого навчання; підтримує пізнавальну активність учнів.

Фаза побудови знань – учитель підводить учнів до формулювання запитань, пошуку, осмислення матеріалу, відповідей на попередні запитання, визначення нових запитань і намагання відповісти на них. Це друга, або середня, фаза уроку - фаза побудови знань.

Ця фаза відбувається в основній частині уроку й має на меті:

порівняти очікування учнів із тим, що вивчається;
переглянути очікування та висловити нові;
виявити основні моменти;
відстежити процеси мислення (перебіг думок учнів);
зробити висновки й узагальнення матеріалу;
поєднати зміст уроку з особистим досвідом учнів;
поставити запитання до вивченого на уроці матеріалу.

На фазі побудови знань учні: здійснюють контакт з новою інформацією; намагаються зіставити цю інформацію з уже наявними знаннями і досвідом; акцентують свою увагу на пошуку відповідей на виниклі раніше питання і труднощі; звертають увагу на неясності, намагаючись поставити нові питання; прагнуть відстежити сам процес знайомства з новою інформацією, звернути увагу на те, що саме привертає їхню увагу, які аспекти менш цікаві і чому; готуються до аналізу й обговорення почутого або прочитаного. Учитель стимулює діяльність учнів, заохочує такі методи як аналіз, синтез і порівняння.

Фаза консолідації – учитель спонукає учнів до рефлексії, про що дізналися, та запитати себе, що це означає для них, як це змінює їхні попередні уявлення, зрештою, як вони зможуть це використовувати.

Фаза консолідації має на меті:

узагальнити основні ідеї;
інтерпретувати визначені ідеї;
обмінятися думками;
виявити особисте ставлення;
апробувати ці ідеї;
оцінити, як відбувається процес навчання;
поставити додаткові запитання.

На цьому етапі уроку відбувається:

осмислення учнями нового матеріалу;
адаптація нових понять в особистій системі знань учня, тобто зміна вже існуючого уявлення;
реструктуризація сформованих зв'язків, що формує місце для нової інформації;
засвоєння й закріплення знань.

Методи навчання математики у структурі уроку критичного мислення

Серед завдань освітньої галузі «Математика» є розвиток логічного, критичного і творчого мислення учнів, здатності чітко та аргументовано формулювати і висловлювати свої судження. При вивченні математики створюються плідні умови формування критичного мислення учнів. Формування критичного мислення учнів відповідає цілям викладання математики, а саме: засвоїти математичні концепції та способи вирішення проблем; отримувати нові знання шляхом розв’язання проблем у автентичних контекстах, використовуючи власні методи під керівництвом учителя; застосовувати орієнтоване на учнів, на їхній власний досвід активне та кооперативне навчання; використовувати дослідження та відкриття.

Методи навчання математики можна впорядкувати таким чином:

1) активізація уваги школярів (мотивація, метод збудження інтересів, метод проблемних ситуацій, метод стимулювання);

2) вивчення нового матеріалу (заучування, метод доцільних задач, конкретно-індуктивний метод, абстрактно-дедуктивний метод, сократичний метод, евристичний метод, дослідницький метод, проскриптивний метод, інскриптивний метод);

3) закріплення знань (метод супровідного закріплення, метод повторення, метод вправ);

4) навчання розв’язування задач та вправ (метод наслідування, метод спроб та помилок, метод поступового ускладнення, метод евристичних наставлянь).

У таблиці 1.3.1. наведено відповідність методів навчання математики та методів критичного мислення структурі уроку критичного мислення. Застосовування трифазової моделі уроку технології розвитку критичного мислення дозволяє ефективно забезпечувати розвиток в учнів стратегії та навичок навчання, забезпечує засвоєння учнями змісту навчальної програми через активне використання на уроках запитань і завдань високого рівня складності, які вимагають застосування учнями мисленнєвих операцій аналізу, синтезу, оцінювання.

Таблиця 1.3.1.

Структура уроку критичного мислення

Методи навчання математики

Збудження інтересу

Мотивації

Проблемних ситуацій

Доцільних задач

Стимулювання

Конкретно-індуктивний

Фаза актуалізації

Методи критичного мислення

Швидке письмо

Семантична карта

Ходимо навколо, говоримо навколо

Обміркуйте – Об'єднайтесь у пари – Обміняйтесь думками

Фаза побудови знань

Методи навчання математики

Заучування

Конкретно-індуктивний

Абстрактно-дедуктивний

Сократичний

Евристичний

Дослідницький

Проскриптивний

Інскриптивний

Супровідного закріплення Наслідування

Спроб та помилок

Методи критичного мислення

«Знаю – Хочу дізнатися – Дізнався»

Схема Венна

Семантичний аналіз ознак

Т-схема

Фаза консолідації

Методи навчання математики

Вправ, повторення

Поступового ускладнення

Евристичних наставлянь

Методи критичного мислення

Нова проблема

Семантична карта

Під час вивчення математики можуть бути сформовані такі уміння критичного мислення учнів:

набуття навичок наукової аргументації при доведенні теорем;
здатність до аналізу, синтезу, узагальнення, класифікації, розпізнавання, співставлення і протиставлення;
розвиток контрольно-аналітичних умінь при виконанні взаємообернених операцій;
здатність до виявлення переваг того чи іншого способу розв’язання завдань;
уміння виробляти альтернативні варіанти і вибирати найоптимальніший.

РОЗДІЛ 2. МЕТОДИ І ПРИЙОМИ НАВЧАННЯ В ПРОЦЕСІ РОЗВИТКУ КРИТИЧНОГО МИСЛЕННЯ

2.1. Характеристика методів та прийомів технології розвитку критичного мислення

Розвиток критичного мислення досягається застосуванням різних методичних стратегій, які використовуються на окремих етапах заняття. Успіх навчання критичному мислення залежить від того, які методи та прийоми вибрати оптимально залежно від теми і мети уроку, так як вони є важливим компонентом кожного уроку.

МЕТОД «СЕМАТИЧНА КАРТА»

Стратегія «Асоціативний кущ чи сематична карта» спонукає до вільного й відкритого мислення, тому цю стратегію рекомендується використовувати на етапах актуалізації і рефлексії. Для складання асоціативного куща слід дотримуватись наступних правил.

Крок 1: записати на дошці чи аркуші в центрі ключове слово (фразу), обвести його (її) колом чи прямокутником.

Крок 2: записати всі слова (фрази), які спадають на думку.

Крок 3: після того як заповнені всі можливі «гілки», вказати аспекти проблеми, що потребують додаткової інформації.

Крок 4: поставити знаки питання біля частин куща, в яких є невпевненість.

Крок 5: записати всі ідеї, які є, або скільки дозволяє час.

МЕТОД «ШВИДКЕ ПИСЬМО»

Мета методу: мотиваційна діяльність учнів.

Суть методу. Метод «Швидке письмо» дає можливість написати щось із певної теми чи розкрити питання протягом 2-5 хвилин.

Початком, підказкою для учнів може бути незакінчене речення, яке вони дописують.

Учні мають писати швидко й без відривання ручки чи олівця від паперу. Мають бути зосереджені на тому, що пишуть, а не як пишуть.

МЕТОД «ЧИТАННЯ В ПАРАХ – УЗАГАЛЬНЕННЯ В ПАРАХ»

Мета методу: спільне кооперативне навчання, яке дозволяє проявити учням більше ініціативи у процесі власного навчання та навчання один одного.

Суть методу. Метод призначений для того, щоби сприяти різним видам мислення, а вся діяльність у сукупності спрямована на покращення розуміння тексту учнями.

Це метод застосовують, коли учні в парах уважно читають текст, щоб досягти його розуміння.

Крок1: у тексті мають бути короткі абзаци (не більше трьох речень у кожному).

Крок 2: якщо цей метод є новим для учнів, учителю потрібно спочатку продемонструвати його:

а) прочитати вголос абзац і узагальнити його зміст. Пояснити, що це одна з двох ролей при виконанні цього завдання. Пояснити, що таке узагальнення, як його треба виконувати: воно коротше, ніж текст, але містить усі його основні ідеї;

б) поставити два запитання за текстом і попросити учнів відповісти на них. Пояснити, що це друга з двох ролей при виконання цього завдання.

Крок 3: попросити учнів об’єднатися у пари. Пояснити, що один із них прочитає перший абзац і узагальнить його. Перевірити розуміння, попросивши кількох учнів зробити узагальнення. Якщо необхідно, прокоментувати відповіді. Потім попросити другого учня в парі поставити запитання до цього абзацу. Після того, як вони це зробили, перевірити розуміння, попросивши кількох учнів оголосити свої запитання. Ще раз, якщо необхідно, зробити коментарі, сказавши, як можна краще поставити запитання.

Крок 4: коли учні зрозуміють, як виконується таке завдання, попросити їх продовжувати роботу самостійно – читати, узагальнювати та ставити запитання за текстом – абзац за абзацом. Нагадувати їм про необхідність мінятися ролями.

МЕТОД «ОБМІРКУЙТЕ – ОБ'ЄДНАЙТЕСЬ У ПАРИ – ОБМІНЯЙТЕСЬ ДУМКАМИ»

Мета методу: залучити до обговорення чи навчання всіх учнів класу. Вона дає можливість кожному учневі висловити свою думку, поділитися з однокласниками своїми знаннями, повчити одне одного.

Метод використовується для того, щоб учні придумали власні відповіді на поставлене вчителем запитання і у парах поділилися своїми відповідями з партнером. Потім учитель викликає дві чи три пари та пропонує їм поділилися своїми відповідями з усім класом.

МЕТОД «ЗНАЮ – ХОЧУ ДІЗНАТИСЯ – ДІЗНАВСЯ»

Мета методу: нагадати учням те, що вони знають, і сформулювати питання, які допомагають спрямувати їхній пошук для кращого розуміння теми.

Суть методу. Метод можна використати для того, щоби структурувати цілий урок. У процесі роботи учнів спочатку пропонують подумати над тим, що вони вже знають з теми цього уроку, поставити запитання з цієї теми та знайти відповіді на ці запитання.

Крок 1: ознайомити учнів з темою уроку. Запропонувати подумати, що вони знають із цієї теми, але попередньо попрацювати в парах і скласти список своїх ідей.

Крок 2: накреслити таблицю на дошці або на великому аркуші паперу.

Крок 3: учні висловлюються і називають те, що їм відомо з цієї теми (думки учнів організовувати у процесі їх висловлювання). Записати їхні ідеї в колонку «Що знаємо?».

Крок 4: учні аналізують вже відоме та відзначають, де їхні знання є неповними з цієї теми. Записати запитання до таблиці в колонку «Про що хочемо дізнатися?» (якщо необхідно, додати свої власні запитання).

Крок 5: учні вивчають (виконують) завдання. Учитель нагадує учням, щоб вони шукали відповіді на свої запитання та відзначали всі нові ідеї, яких не очікували.

Крок 6: учні повідомляють про те, що вони дізналися, дають відповіді, які знайшли на свої запитання, а потім – усі цікаві або важливі ідеї, які виявили. Записати в колонку «Про що дізналися?».

Що знаємо?	Про що хочемо дізнатися?	Про що дізналися?

МЕТОД «ЩО? – ОТЖЕ, ЩО? - ЩО ТЕПЕР?»

Мета методу полягає в тому, щоб допомогти учням знайти взаємозв’язки між ідеями, досліджуваними на уроці та ідеями в житті. За допомогою цього методу учні вчаться знаходити основні ідеї в тексті, розмірковувати про практичні наслідки цих ідей, а також обирати та здійснювати дії на їх основі.

Передбачається, що наступне обговорення теми уроку буде спиратися на наявне в учнів загальне розуміння теми на рівні основних ідей.

На дошці або великому аркуші паперу вчитель креслить таблицю.

Що?	Отже, що?	Що тепер?

Що? Указуючи на колонку «Що?», учитель пропонує учням підсумувати найбільш важливі ідеї, які вони щойно обговорювали з даної теми. Після обговорення вчитель записує узагальнені ідеї до колонки «Що?».

Отже, що? Далі вчитель просить учнів подумати, що є важливим в цих ідеях, які вони щойно перелічили. Чому вони мають значення? Після обговорення вчитель записує узагальнені пункти до колонки «Отже, що?».

Потім учитель запитує учнів, що вони можуть зробити стосовно цього питання, яке обговорювали. Генерування ідей та їх опрацювання записуються у колонку «Що тепер?».

МЕТОД «СХЕМА ВЕННА»

Мета методу: визначати зв'язки між поняттями, їх властивостями, критерії порівнюваних об’єктів; складати класифікаційні схеми.

Суть методу. Метод передбачає створення графічної схеми з двох чи трьох кіл, які частково накладаються одне на одне.

Крок 1: пояснити учням, що дана діаграма – це два (чи три) кола, які частково накладаються одне на одне. Частина діаграми лівого кола використовується для запису властивостей, характерних лише для першого поняття. Частина діаграми правого кола – для запису властивостей, характерних лише для другого поняття. Перетин кіл використовується для запису спільних властивостей.

Крок 2: надати правила вільного виконання класифікації понять: встановіть ознаки об'єктів, що мають бути класифіковані; виберіть ознаку (можна декілька), за якою буде проводитися класифікація; порівняйте між собою об'єкти за спільними і спеціальними ознаками.

Крок 3: учні будують діаграму і записують спільні ознаки в спільній частині діаграми, розбіжності в ліву та праву частини.

Встановлення ознак для учнів дуже складна робота, тому вчитель повинен допомагати їм, особливо спочатку.

Метод дає можливість:

учителю: формувати в учнів навички порівняння та класифікації;

учням:

глибше зрозуміти зв'язки між поняттями, їх властивостями;
навчитися класифікувати з допомогою схеми;
зрозуміти структуру інформації;
узагальнювати інформацію на високому рівні;
складати складні класифікаційні схеми;
ефективно поглиблювати знання;
створювати критерії порівнювання об'єктів.

МЕТОД «СЕМАНТИЧНИЙ АНАЛІЗ ОЗНАК»

Семантичний аналіз ознак спрямований на забезпечення розуміння змісту тексту і передбачає:

виділення і осмислення: окремих слів, термінів, понять, як життєвих, так і математичних, граматичних конструкцій ( “якщо ... то”, “після того, як ...” і т.д.), кількісних характеристик об'єкта, що задаються словами “кожного”, “якого-небудь”, “будь-який”, “деякий”, “всього”, “все”, “майже всі”, “однакові”, “стільки ж”, “порівну” і т.д.;
відновлення предметної ситуації, описаної в тексті, шляхом спрощеного переказу тексту з виділенням тільки істотної для вирішення завдань інформації;
виділення узагальненого сенсу завдання – ( про що йдеться в задачі, вказівка на об'єкт і величину, яка повинна бути знайдена (вартість, обсяг, площа, кількість і т.д.).

МЕТОД Т-СХЕМА

Мета методу: розвиток в учнів уміння аналізувати текст, знаходити аргументи.

Суть методу. Метод Т-СХЕМА (Т-таблиця) використовується для аналізу інформації, пошуку аргументів.

Крок 1: поділіть аркуш паперу навпіл або намалюйте велику літеру Т.

Крок 2: в одній половині таблиці запишіть всі аргументи, які підтримують ідею автора, в іншій – протилежні.

ПРИЙОМ ІНСЕРТ

Інсерт – звуковий аналог умовного англійського скорочення в дослівному перекладі позначає: інтерактивна система запису для ефективного читання й міркування.

Мета: прийом сприяє розвитку аналітичного мислення, є засобом відстеження розуміння матеріалу.

Прийом здійснюється в кілька етапів.

І етап: пропонується система маркування тексту, щоб розділити укладену в ньому інформацію в такий спосіб:

«+» – знаком «плюс» позначається інформація, яка вже відома учню;

«–»–знаком «мінус» позначається те, що йде врозріз з наявними в учня уявленнями, переконаннями;

«!»– «знаком оклику» позначається нова інформація, яка є для учня цікавою і несподіваною;

«?» – «знак питання» ставиться, якщо щось залишилося незрозумілим, вимагає додаткових відомостей, викликає бажання дізнатися докладніше.

ІІ етап: читаючи текст, учні позначають відповідним значком на полях окремі абзаци й пропозиції. Знайомство з текстом може здійснюватися «на слух».

ІІІ етап: учням пропонується систематизувати інформацію, розташувавши її у відповідності зі своїми позначками в наступну таблицю:

+	-	!	?

ІV етап: послідовне обговорення кожної графи таблиці.

ПРИЙОМ КЛАСТЕР

Кластер – спосіб графічної організації матеріалу, що наочно відображає думки під час вивчення тієї чи іншої теми. Інколи цей спосіб називають «наочним мозковим штурмом».

Мета: встановлення максимальної кількості ознак явища, що вивчається.

Посередині чистого аркуша (дошки) напишіть ключове слово або речення, що є «серцем» ідеї, теми.
Навколо запишіть слова або речення, що відображають ідеї, факти, уявлення по темі, що вивчається (модель «планети та її супутників»).
Під час запису нові слова з’єднуйте прямими лініями з ключовим поняттям. У кожного із «супутників», відповідно, також з’являються «супутники», установлюються нові логічні зв’язки.

Під час роботи необхідно дотримуватися наступних правил.

Записувати всі ідеї, що пропонуються.
Намагатися побудувати якомога більше зв’язків.

2.2. Організації навчальної діяльності учнів на уроках математики з використанням технології розвитку критичного мислення

УРОК З АЛГЕБРИ, 10 КЛАС

Тема. Похідна та її застосування

Цілі уроку:

Освітня компетентність: узагальнити та систематизувати знання та вміння учнів з теми, удосконалити вміння та навички учнів розв’язувати задачі на застосування похідної, продовжити підготовку до зовнішнього незалежного тестування.

Розвиваюча компетентність: розвивати пізнавальний інтерес, навички роботи з тестами, логічне мислення.

Виховна компетентність: виховувати працьовитість, зібраність, організованість, старанність, відповідальність та вимогливість до себе.

Тип уроку: удосконалення знань, умінь та навичок

Форма роботи: колективно-групова

Наочність: підручник, таблиці, картки з тестами, рисунки з графіками функцій

Обладнання: ПК комп’ютерний клас, презентація, таблиця похідних.

СТРУКТУРА УРОКУ

І. Організаційна частина.

Привітання, перевірка готовності до уроку.

Налаштування на робочу обстановку

Рефлексія (Анаграма настрою)

«Недостатньо лише мати гарний розум,

головне – це добре застосовувати його»

Р. Декарт

ІІ. Мотивація навчальної діяльності. Оголошення теми та завдань уроку.

На попередніх уроках ви засвоїли одне із фундаментальних понять алгебри та початків аналізу – похідну. ЇЇ появі ми завдячуємо таким вченим, як П.Ферма, І.Ньютон, Г.Лейбніц, Ж.Лагранж.

Поняття похідної широко застосовується у механіці, військовій справі, медицині, космонавтиці, фізиці, астрономії. Тому і приділяється така увага цьому поняттю.

ІІІ. Актуалізація опорних знань учнів "ПОВТОРИ"," ЗОРІЄНТУЙСЯ "

інтерактивні вправи: колективна робота «Теоретичний бліц-турнір»,

прийом «Знайди помилку», прийом «Чи правильно, що…», «Знайди пару».

ІV. Повідомлення теми, мети і завдань уроку "ВИВЧИ"

Компетентності учнів (мета)

Я ЗНАТИМУ (Пригадайте)___

Я ВМІТИМУ (Створіть)_____

Я МОГТИМУ (Пам‘ятайте)_____

V. Застосування вмінь та навичок "ВІДТВОРИ" "ЗАПАМ‘ЯТАЙ"

Робота по групах

Інтерактивні вправи

VI. Домашнє завдання "ДОСЛІДЖУЙ ВДОМА"

VII. Підсумок уроку

Карта уроку

ІІІ. ✍ ПОВТОРИ

Колективна робота

Теоретичний бліц-турнір

Група вибирає поняття на дошці і відразу відповідають. Неправильні відповіді виправляють самі учні (і лише за необхідності – вчитель). За правильну відповідь учні виставляють у лист оцінювання кількість набраних балів.

Для учнів зі слабкими знаннями використовується прийом «Незакінчене речення» .

1. Дати означення похідної?	Число, яке дорівнює границі відношення приросту функції до відповідного приросту аргументу за умови, що приріст аргументу прямує до нуля
2. Що таке похідна з механічної точки зору?	S`(t) = V(t); V`(t)=а(t)
3. В чому полягає геометричний зміст похідної. Рівняння дотичної	Якщо функція в деякій точці х_о має похідну, то в цій точці визначено дотичну до графіка функції, при чому її кутовий коефіцієнт дорівнює f`(x₀). Рівняння дотичної y= f^/(x₀)(x-x₀) + f(x₀)
4. Сформулюйте правила диференціювання
5. Ознака зростання функції	Якщо для всіх x з деякого проміжку f`(x) > 0 то функція зростає на цьому проміжку
6. Ознака спадання функції	Якщо для всіх x з деякого проміжку f`(x) < 0 то функція спадає на цьому проміжки
7. Назвіть ознаку точки максимуму функції	Якщо при переході через точку x₀ похідна змінює знак з плюса на мінус, то x₀ – точка максимуму
8. Ознака точки мінімуму функції	Якщо при переході через точку x₀ похідна змінює знак з мінуса на плюс, то x₀ – точка мінімуму
9. Які точки можуть бути екстремальними?	Якщо точка x₀ є точкою екстремуму функцій то f`(x) = 0 або f не є диференційованою в цій точці її називають критичною.
10. Назвіть етапи алгоритму дослідження функції для побудови її графіка

ЗОРІЄНТУЙСЯ

Прийом «Знайди помилку»

(1 учень біля дошки):

Розвязування завдань

Прийом «Чи правильно, що…»

Функція зростає на [-7;2) і (2;8] значить вона зростає на [-7;8] (Ні)
Критична точка є точкою екстремуму. (Ні)
Точка екстремуму є критичною (Так)
Точки на графіку x₁=1, x₂=-1, x₃ = 2 є точками максимуму. (Ні)

графік

Знайди пару

Знайти похідну функції та відповідний до неї графік.

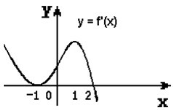
Створити логічну пару: функція+похідна+графік.

Рисунок1

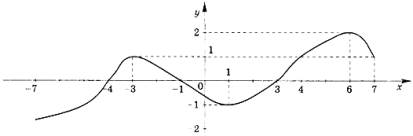
ОБРОБИ ІНФОРМАЦІЮ

На рисунку зображено графік функції f(х), визначеної на відрізку [-7;7]. Скільки нулів матиме функція f^/(х) на проміжку (-7;7)?

графік функції

ІV. ВИВЧИ

Тема уроку.

Похідна та її застосування

Компетентності учнів на уроці (цілі)

Я знатиму (освітня)

розв’язувати задачі на застосування похідної

Я вмітиму (розвиваюча)

використовувати теоретичні знання з теми

при розв’язанні практичних задач

Я зможу (виховна)

впевнено себе почувати під час ДПА та ЗНО,

де досить прості в розв’язанні задачі мають

достатньо нестандартний зміст

V. ВІДТВОРИ

Робота в групах

І група. Знайти точки екстремуму функції.

Розв’язання: у'=4х³-4х

4х³-4х=0, х(х²-1)=0, х(х-1)(х+1)=0

Відповідь: х _max=0; х _min=-1;1.

ІІ група. Знайти найбільше та найменше значення функції на проміжку [-3;2] .

Розв’язання:

f(-3)=81-18-3=60

f(-1)=1-2-3=-4

f(0)=-3

f(2)=16-8-3=5

Відповідь: f _max=60; f _min=-4.

ІІІ група. Знайти проміжки зростання та спадання функції

x	(-∞;-1)	-1	(-1; 0)	0	(0; 1)	1	(1;+∞)
*f′ (x)*
*f (x)*

Розв’язання:

x	(-∞;-1)	-1	(-1; 0)	0	(0; 1)	1	(1;+∞)
*f′ (x)*	-		+		-		+
*f (x)*

Відповідь: зростає (-1;0)U(1;+∞)

спадає (-∞;-1)U(0;1)

ІV група. Знайти критичні точки функції

Розв’язання: у'=4х³-4х

4х³-4х=0, х(х²-1)=0, х(х-1)(х+1)=0

х=0, х=1, х=-1

! ЗАПАМ‘ЯТАЙ

Задача. Знайдіть число коренів рівняння -х³+3х-2=а, якщо а (-4; 0).

Ґрунтовні знання з теми “Похідна” допоможуть Вам без проблем розв’язувати будь-які задачі, пов’язані з похідною.

Існують різні способи розв’язування рівнянь з параметрами, один з них – графічний.

Графічний метод розв’язання рівнянь є доцільним, коли рівняння містить функції з різних класів: наприклад, степенева і тригонометрична, степенева і показникові, тощо.

Додатковою ознакою необхідності застосування цього методу є завдання на знаходження кількості коренів рівняння, а не самих коренів.

(Коментоване поетапне повне розв’язування задачі на дошці)

Виконання завдань у форматі ЗНО.

Виконання тестів – надійний шлях до здачі ЗНО

Тести на картках

№ п/п	Запитання	а)	б)	в)	г)
1	Розв’язати рівняння у’=0, якщо у=х²-4х	-2	-4	2	4
2	Знайти критичну точку функції у=2х²-4х	-1	1	0	2
3	Знайти проміжок зростання функції у=х²-2х-3	(-∞; 1)	(1; ∞)	(-1; 1)	(0; ∞)
4	Розв’язати нерівність у’²	(-∞; ∞)	(-∞; 5)	(5; ∞)	(-5; ∞)

VI. ДОСЛІДЖУЙ ВДОМА

Обговорення заробітної плати

Знайти максимум функції.

(Заробітна плата становить 12 тисяч гривень)

VII. ПІДСУМОК УРОКУ

Сьогодні на уроці ми…
Найважливішим на уроці для мене було…
Найбільше зацікавило…
Найскладнішим для мене було…
Щоб усунути прогалини в знаннях, я маю…

УРОК З АЛГЕБРИ, 10 КЛАС

Тема уроку. Числові функції. Способи задання числових функцій.

Мета уроку: повторити і узагальнити поняття функції, числової функції, області визначення і області значення функції, графіка функції, способів завдання функції. Удосконалювати вміння знаходити область визначення і область значення функцій, заданої аналітично; знаходити значення функції при заданих значеннях аргумента та значення аргумента, при яких функція набуває заданого значення; застосовувати різні способи задання функції; тренувати розумові операції аналіз, синтез, порівняння, узагальнення, розвивати логічне мислення, комунікативні вміння, навички самоконтролю;

виховувати уважність, кмітливість, акуратність, самостійність, самокритичність.

Очікувані результати (уміння критичного мислення, які формуються у процесі вивчення теми): учні зможуть аналізувати, синтезувати й узагальнювати поняття числової функції, області визначення функції, області значень функції; визначати область визначення та область значень функції та застосовувати різні способи задання функції.

Обладнання та наочність: підручник, роздатковий матеріал, комп’ютер. Тип уроку: узагальнення та систематизація знань, вмінь і навиків.

ХІД УРОКУ

Організаційний етап.

Перевірка готовності учнів до уроку, налаштування на роботу.

І. АКТУАЛІЗАЦІЯ (передбачення)

Учитель починає урок зі структурованого огляду: коротке повідомлення теми (для спрямування думки учнів на тему уроку та з метою викликати у них зацікавленість).

На практиці часто доводиться зустрічатися з різними відповідностями, тобто правилами, за якими одним об'єктам (елементам) ставляться у відповідність інші.

Ось деякі приклади таких відповідностей:

кожному місяцю в році ставиться у відповідність число днів у цьому місяці;
кожному числу відповідає його модуль;
при вимірюванні відрізків кожному відрізку ставиться у відповідність число, що виражає його довжину;
при сталій ціні кожній певній кількості предметів ставиться у відповідність їхня вартість.

Розглянемо відповідність: кожному числу ставиться у відповідність деякий його дільник

10	2
24	3
33	5
55

Який висновок можна зробити?

Учні аналізують запропоновані відповідності.

Всі ці відповідності можна розділити на групи за різними ознаками. Але є серед них абсолютно особливі. Це такі відповідності, при яких кожному елементу однієї множини зіставляється єдиний елемент іншої множини.
Такі відповідності і називаються функціями.

Метод «Обміркуйте – Об'єднайтесь у пари – Обміняйтесь думками»

Завдання учням: подумайте і запишіть відповідність, досліджуючи явища природи, фізичні, хімічні, біологічні процеси. Потім поверніться до свого партнера – учня, який сидить поруч та обміняйтеся своїми відповідями. Учитель запрошує до відповіді учнів:

площа прямокутника залежно від довжини однієї зі сторін;
залежність температури повітря, атмосферного тиску від пори року;
кардіограма, температура тіла і т.д.

Учитель: для вивчення цих процесів потрібно створити математичну модель. І однією з таких моделей є функція.

Основною метою вивчення теми є формування уявлення про функції як математичної моделі залежності між величинами й об'єктами будь-якої природи

Пропоную вам скласти математичні моделі залежностей:

залежність між радіусом і довжиною кола; (С=2πr)
залежність між швидкістю і відстанню при умові, що t =const,; ( v= )
залежність тиску газу та його об’єму за сталої температури (рV=const, закон Бойля-Маріотта)

Спільним для цих задач є їх математичний зміст, а саме: є дві числові множини (X, Y), кожному числу однієї з них ставиться у відповідність єдине число другої - у = f (х). Ми застосували поняття числової функції.

X Y

Виконання вправ:

1.При яких значеннях х має зміст вираз:

х + 3; (х - 8)²; ; ?

2. При яких значеннях х значення виразу х² + 7 дорівнює 32; 56; -2?

Учитель підводить учнів до самостійного осмислення теми.

Метод «Незакінчене речення»

Продовжіть речення:

1) функція – це…

2) область визначення функції – це…

3) області визначення функцій та - це …,

4) область значення функції – це…

5) область значення функції у=, це…

6) для функції f (х) = знайти , f (3), f (-3)…

7) значення функції дорівнює 6, якщо дорівнює…

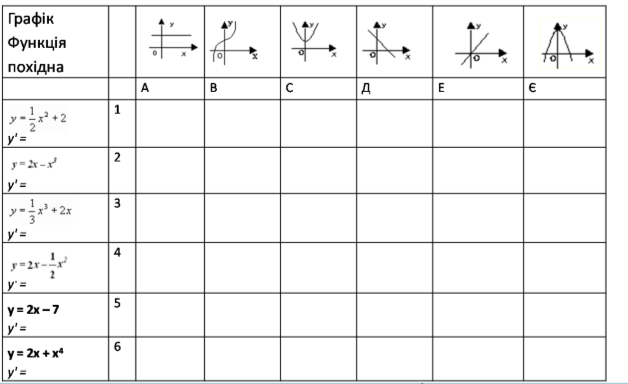
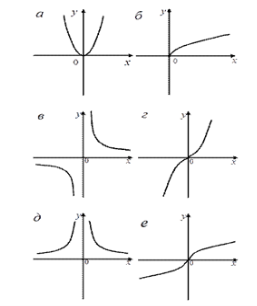
2. Встановіть відповідність між функціями та їх графіками:

1
2
3
4
5
6

Перевірка завдань. Відповіді на дошці.

Учитель рекомендує учням об’єднатися у пари і скласти список того, що вони знають про функцію.

Учитель креслить на дошці таблицю «ЗНАЄМО – ХОЧЕМО ДІЗНАТИСЯ – ДІЗНАЛИСЯ».

ФУНКЦІЯ

Що знаємо?

Про що хочемо дізнатися?

Про що дізналися?

Учитель пропонує парам учнів назвати основні відомості про функцію, з якими вони ознайомилися в 7-9 класах і записує їх у графі «Що знаємо?».

Питання:

Що називають аргументом функції?
Що називають значенням функції?
Що називають область визначення функції?
Що називають областю значень функції?
Якими способами можна задавати функції?

Учитель запитує в учнів про те, у чому вони не впевнені. Учні відповідають і ці питання учитель записує у стовпчик «Про що хочемо дізнатися?»

ІІ. ПОБУДОВА ЗНАНЬ

Учитель пропонує учням об’єднатися у чотири групи та опрацювати текст у підручнику:

перша група: область визначення функції;
друга група: область значень функції;
третя група: способи задання функції;
четверта група: графік функції.

Завдання першій і другій групам:

знаходження області визначення функції залежно від її виду

Завдання третій і четвертій групам:

знаходження значення функції при заданих значеннях аргумента та значення аргумента, при яких функція набуває заданого значення

Учитель слухає, як учні узагальнюють опрацьований матеріал. Якщо учні розуміють свої дії, він дає можливість продовжувати роботу, якщо необхідна допомога – втручається та пропонує свою допомогу.

Підсумок роботи груп:

І. Розв’язування вправ.

Двоє учнів біля дошки
1. учень

Побудуйте графіки функцій областю визначення для яких є:

а) множина дійсних чисел, не більше за 3;

б) множина дійсних чисел, крім чисел -2 і 3.

учень

Побудувати графік функції, для якої D(f) = [-2;4] , Е(f) = [-3;3].

Зробити підсумок щодо поведінки графіка у кожному випадку.

Запитання до учнів класу. Чи кожна множина точок координатної площини є графіком деякої функції ? (Завдання 51 підр.ст.27)

Клас самостійно розв’язує завдання з підручника № 54 (1,3,4,6) ст. 28.

Перевірка виконаного завдання.

Запитання до учнів класу. Що є областю визначення функкції, якщо функцію задано формулою і не вказано її область визначення?

ІІ. Колективне розв’язування завдання.

Знайдіть область визначення, область значень функції

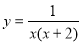
Відповідь:D(y)=(-∞;-2)U(-2;0)U(0;+∞); E(y)=(-∞;0)U(0;+∞).

Коментоване розв’язування.

Знайдіть область значень функції

D(y)=(-∞-2)U(-2; +∞), E(y) - ?

Виділимо цілу частину в дробу

Оскільки виразне може набувати значення, що дорівнюють нулю, то функція не може набувати значення, що дорівнюють 1.

Відповідь: E(y) =(-∞;1)U(1; +∞).

ІІІ. Завдання для самостійної роботи.

В – 1

1.f(x) = x²+ x. Знайдіть f(-2).

а) 6; б) 2 ; в) -2 ; г) 4.

2. Знайдіть область визначення функції f(x) = .

а) (-∞;+∞); б) (-∞; 1)U(1;+∞); в) (-∞; 1); г) (-∞; 0)U(0;+∞).

3. Знайдіть область значень функції f(x) = x²- 2.

а) R; б) [2;+∞); в) [-2;+∞); г) (-∞;-2].

В – 2

1.f(x) = x³+ 2x. Знайдіть f(-1).

а) 1; б) 3 ; в) -3 ; г) 4.

2. Знайдіть область визначення функції f(x) = .

а) (-∞;+∞); б) (-∞; -1)U(-1;+∞); в) (-∞; 2); г) (-∞; -2)U(-2;+∞).

3. Знайдіть область значень функції f(x) =- x²+2.

а) R; б) [2;+∞); в) [-2;+∞); г) (-∞;2].

ІІІ. КОНСОЛІДАЦІЯ

Учитель: відновіть етапи вивчення вами даної теми, пригадайте основні результати своєї діяльності на уроці.

Результати оформіть у вигляді таблиці.

Метод «СЕМАТИЧНА КАРТА»

Завдання: скласти теоретичні опори навчального матеріалу сьогоднішньої теми

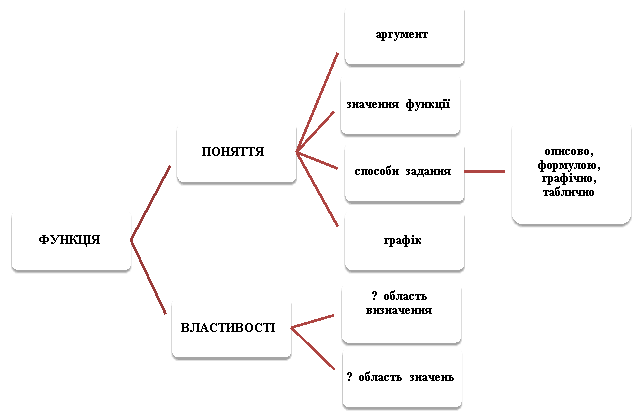
Узагальнення таблиці «ЗНАЄМО – ХОЧЕМО ДІЗНАТИСЯ – ДІЗНАЛИСЯ»

Учні обмірковують, переосмислюють те, що вони знали до уроку, у контексті того, що вони вивчили. Заповнюється колонка «Про що дізналися?».

Учитель:

Проаналізуйте ефективність своєї роботи на уроці?
Ви запам’ятовували деталі, знаходили основні ідеї чи інтерпретували?
Що ви винесли з цього уроку? – Інформацію, важливі ідеї чи навички мислення?

Домашнє завдання

§ 2, опрацювати п.3 (ст. 20-21)

Виконати № 47, № 53, № 55 (1,2,4).

УРОК З АЛГЕБРИ, 9 КЛАС

Тема уроку. Квадратна нерівність. Розв'язування квадратних нерівностей.

Мета уроку: сформувати знання учнів про зміст поняття «квадратна нерівність», домогтися розуміння та засвоєння учнями схеми розв'язування квадратних нерівностей із використанням побудови графіка квадратичної функції;

розвивати логічне та критичне мислення учнів, графічні навички, просторову уяву, уміння обґрунтовувати власну позицію;

виховувати уважність, кмітливість, акуратність, самокритичність та вміння працювати в команді і в парах.

Обладнання: підручник, роздатковий матеріал, комп’ютер.

Тип уроку: засвоєння знань, формування вмінь.

ХІД УРОКУ

Організаційний етап.

Перевірка готовності учнів до уроку, налаштування на роботу.

І. АКТУАЛІЗАЦІЯ

Для актуалізації у пам’яті учнів уже наявних знань, осмислення того, що вони вже знають, учитель пропонує учням до кожного з ключових слів, використавши метод «ШВИДКЕ ПИСЬМО», дати означення, пояснення, навести приклади, якщо вони потрібні для розкриття поняття протягом 2-5 хвилин.

Ключові слова: квадратний тричлен, квадратична функція, парабола, область визначення і область значень, нерівності.

Метод «Що? – ОТЖЕ, ЩО? - ЩО ТЕПЕР?»

Учитель креслить на дошці таблицю.

Що?

Отже, що?

Що тепер?

Учитель пропонує учням у колонку «Що?» підсумувати основні поняття, які вони щойно осмислювали. Записує ідеї учнів у колонку.

Запитання до учнів:

Що є графіком квадратичної функції?
Від чого залежить напрям віток параболи?
Які можливі випадки розміщення графіка квадратичної функції в залежності від знаку дискримінанта при а > 0?
Які можливі випадки розміщення графіка квадратичної функції в залежності від знаку дискримінанта при а < 0?

Виконайте завдання.

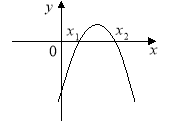
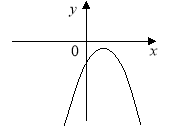
1.На рисунку зображено графік функції у = ах² +bх + c. Визначте знаки коефіцієнтів а, b і c.

	a > 0, b > 0, c > 0;
	a > 0, b > 0, c < 0;
	a > 0, b < 0, c > 0;
	a > 0, b < 0, c < 0;
	a < 0, b > 0, c > 0;
	a < 0, b > 0, c < 0;
	a < 0, b < 0, c > 0;
	a < 0, b < 0, c < 0. Відповідь: 8.

2.На рисунку зображено графік функції у = ах² +bх + c. Визначте знаки коефіцієнта a і дискримінанта D.

a > 0, D > 0;

a < 0, D > 0;

a > 0, D < 0;

a < 0, D < 0.

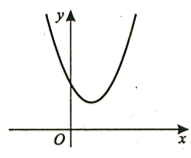
$Описание: C:\Documents and Settings\Администратор\Мои документы\My Pictures\Scan Pictures\20100511\Image5.bmp$

Відповідь: 3.

3.Дано вирази:

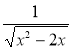1) ; 2) ; 3) .

Укажіть нерівність, яка є записом умови існування кожного з даних виразів:

а) х ≥ 0; б) х > 0; в) ≥ 0; г) х²– 2х ≥ 0; д) х²– 2х > 0.

Відповідь: 1-б; 2-д; 3 –г.

ІІ. ПОБУДОВА ЗНАНЬ

Завдання: використайте схему Венна для визначення зв'язків між поняттями: квадратне рівняння, квадратична функція, нерівності.

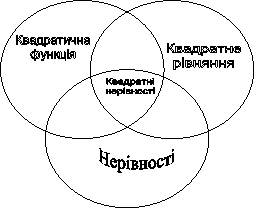Відповідь: квадратні нерівності.

Отже, що? Подумайте, що є важливим, які знання у вас уже є з даної теми? Які кроки ви пропонуєте для вирішення цих питань?

Крок 1. Означення квадратної нерівності. Приклади квадратних нерівностей з різними коефіцієнтами.

	*Нерівності виду ах² + bх + с >* 0 (<0; ≥ 0; ≤ 0) *називаються квадратними, якщо а* 0.
	Приклад. 3х²– 2х – 1 > 0, x²– 9 ≥ 0, х²– 2х < 0, - х²> 0 — квадратні нерівності (з різними значеннями коефіцієнтів квадратного тричлена в лівій частині).

Який зміст має зауваження а ≠ 0?

(Відповідь: якщо a = 0 нерівність не буде квадратною).

Зверніть увагу на нерівності виду ах² + с > 0,

(так само, як і квадратний тричлен, квадратна нерівність може мати «скорочений» вигляд).

Після обговорення вчитель записує узагальнені пункти до колонки «Отже, що?».

Що тепер? Учитель запитує учнів, як вони можуть примінити свої знання до розв’язування квадратнних нерівностей? (Відповіді учнів).

Який метод розв’язування квадратного рівняння більш наочний? (графічний)
Яка буде наша мета? Навчитися розв’язувати квадратні нерівності за допомогою графіка квадратичної функції.

Крок 2. Розв'язування квадратних нерівностей за допомогою побудови графіка відповідної квадратичної функції.

Метод «Читання в парах – Узагальнення в парах».

Учитель пропонує учням, використавши метод «Читання в парах – Узагальнення в парах», уважно ознайомитися з алгоритмом розв'язування квадратних нерівностей.

Нагадує учням про необхідність мінятися ролями після обговорення кожного пункту.

	Схема розв'язування квадратних нерівностей
	1. Знайти дискримінант D, а потім корені x₁, x₂ квадратного тричлена (якщо вони існують).
	2. Побудувати ескіз графіка квадратичної функції у = ах² + bх + с (з урахуванням знака коефіцієнта а та знайденого знака дискримінанта D і коренів).
	Для випадку а > 0 відповідно отримаємо проміжок, для якого точки параболи лежать вище осі Ох, для випадку а < 0 відповідно отримаємо проміжки, для яких точки параболи лежать нижче осі Ох.
()

		Розв’язків немає	Розв’язків немає

Крок 3.

Розв’язати нерівність: х²+4х+5 > 0.

Розв’язання

у = х²+4х+5 - квадратична функція, графіком є парабола, вітки якої напрямлені вгору ( а = 1 > 0);

D = - 4 < 0.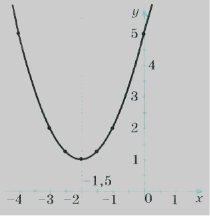

Координати вершини параболи:

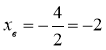
y_в=4-8+5=1;

( -2; 1 ) – вершина параболи.

х= - 2 - вісь параболи.

Координати ще кількох точок параболи:

х=0, у=5 ; (0; 5);

х= -1, у=1-4+5=2 ; (-1; 2).

Відповідь: х²+4х+5 > 0 при всіх значеннях хR.

Запитання до учнів.

Які значення змінної х необхідно знати, щоб записати розв’язок нерівності?
Чи обов'язково точно будувати графік функції.

Висновок. Різні способи розташування графіка квадратичної функції

y = ax²+ bx + c відносно осі Ох залежно від знака старшого коефіцієнта а та знака дискримінанта D квадратного тричлена ах² + bх + с.

Крок 4. У колонку «Що тепер?» запишіть алгоритм розв'язування квадратних нерівностей.

АЛГОРИТМ

1. Приведіть нерівність до виду ().

2. Розгляньте функцію .

3. Визначте напрям віток параболи.

4. Знайдіть точки перетину параболи з віссю абсцис (для них y = 0; знайдітьі , розв’язуючи рівняння ).

5. Схематично побудуйте графік функції .

6. Виділіть частину параболи, для якої y > 0 (y < 0).

7. На осі абсцис виділіть ті значення х, для яких y > 0 (y < 0).

8. Запишіть відповідь у вигляді проміжків.

Розв’язування вправ

Виконати № 399 (1, 9, 15 ) підручник ст.123.
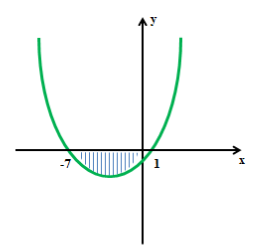
Розв’яжіть нерівність х²+6х-7 < 0.

у = х²+6х-7

Графік – парабола.

а =1 > 0 – вітки параболи направлені вгору.

D = 64 > 0.

= 1; = -7.

Схематично малюємо графік квадратичної функції. Розв’язки нерівності х є (-7; 1).

Відповідь: (-7; 1).

Запитання до учнів

Чому заштрихована саме внутрішня область між точками?

(Відповідь: функція y < 0, тобто графік лежить нижче осі абсцис саме на цьому проміжку).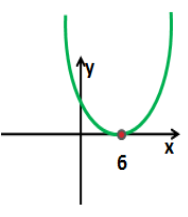

3. Розглянемо випадок, коли D = 0.

Розв’яжіть нерівність х²- 12х+36 ≥ 0.

у = х²- 12х+36, графік – парабола,

а =1 > 0 – вітки параболи направлені вгору,

D =0, == 6.

Відповідь: х є R.

4. Розглянемо випадок, коли D < 0.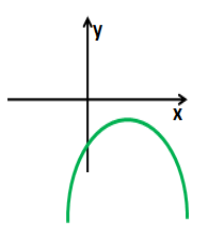

Розв’яжіть нерівність - 4х²+5х-7 > 0.

у = - 4х²+5х-7, графік – парабола,

а = - 4 < 0 – вітки параболи направлені вниз,

D = - 87 < 0,

Відповідь: розв’язків немає.

Прийом «ІНСЕРТ»

Учитель пропонує учням систематизувати інформацію, розташувавши її у відповідності зі своїми позначками в наступну таблицю:

«+» - я це знав;

«-» - я цього не знав;

«!» – це мене здивувало;

«?» - хотів би взнати детальніше.

*х²+4х+5* > 0	!
х²+6х-7 < 0	+
*х²- 12х+36* > 0	?
*-4х²+5х-7* > 0	-

ІІІ. КОНСОЛІДАЦІЯ

Самостійна работа. Одне із завдань виконує група учнів з одного ряду. Три завдання – три групи.

(Для роботи використовуються заздалегідь заготовлені таблиці з формулюванням етапів розв’язання).


1.Визначте значення коефіцієнта а і вкажіть напрямок гілок параболи, що відповідає графіку даної квадратичної функції.
2.Запишіть відповідне квадратне рівняння і знайдіть значення D.
3. Знайдіть корені рівняння (якщо вони є).
4. Зобразіть ескіз графіка відповідної квадратичної функції, використовуючи отримані точки перетину (або дотику) з віссю ОХ.
5. Вкажіть, на яких проміжках функція набуває додатних значень, а на яких від’ємних.
6.Виберіть проміжки, в яких функція приймає значення, які відповідають даній квадратній нерівності і запишіть відповідь.

Учитель контролює хід розв’язування. Після виконання завдання представники груп обмінюються виконувати дане завдання.

Підсумок. Запитання до учнів:

- Що нового ви дізналися на уроці?

- Яку мету ставили?

- Які отримали результати?

- Де можна застосувати нові знання?

- Над чим ще треба попрацювати?

Домашнє завдання

Учням пропонується прочитати матеріал підручника § 2 п.12 (стор.119).

Вивчити означення квадратної нерівності, схему її розв'язування.

Виконати № 400 (1,4.8,9), 402.

ВИСНОВКИ

Пошук шляхів цікавості викладу навчального матеріалу, гаряче прагнення збудити в учнів інтерес до навчання неминуче породжує такі засоби, які роблять процес навчання захоплюючим, виникає потреба у створенні формату нового уроку, що відповідає новим вимогам суспільства. Такими є уроки із запровадження технології розвитку критичного мислення, які містять поєднання репродуктивної та продуктивної діяльності учнів, продуману послідовність етапів навчальної роботи, завдяки чому оптимально розподіляється зміст, підтримується рівень активності учнів, яка спрямована не тільки на активність мислення, а й на підвищення розумових зусиль, на поліпшення процесу засвоєння знань, умінь і навичок, а значить – на підвищення ефективності уроку.

Пріоритетними позиціями сучасного уроку математики є використання найефективніших технологій навчання. Застосування технології розвитку критичного мислення в навчальному процесі як механізму вдосконалення якості викладання математики є тією можливістю розвитку «науки мислити», що дозволить навчити учнів перевтілювати обсяг інформації в знання, а отримані в такий спосіб теоретичні знання – трансформувати в професійні навички та вміння. Використання цієї технології дозволяє удосконалювати і формувати в учнів такі розумові дії, як аналіз, синтез, оцінювання, уміння робити аргументовані висновки, спираючись на попередні знання і практичний життєвий досвід. Методи й прийоми активізують навчальну діяльність учнів, викликають певне емоційне ставлення до інформації, уміння самостійно вчитися, здатність до самопізнання і самореалізації.

В роботі теоретичні положення підтверджено конкретними прикладами методів та прийомів технології розвитку критичного мислення у викладанні математики та наведені варіанти організації навчальної діяльності учнів з використанням технології розвитку критичного мислення у формі розробки уроків.

Найкращого результату формування навичок активної пізнавальної діяльності та критичного мислення можна досягти у тому разі, коли застосування методів і прийомів є системним.

ДОДАТКИ

СЕМАНТИЧНА КАРТА поняття «Рівнобічна трапеція»

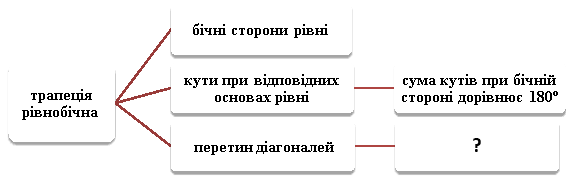
МЕТОД «ЧИТАННЯ В ПАРАХ – УЗАГАЛЬНЕННЯ В ПАРАХ»

Завдання. Опрацювати опорні задачі про перехід між кутами правильної піраміди.

Для правильної трикутної піраміди знайдіть зв’язок між кутами:

двогранним кутом при ребрі основи і кутом нахилу бічного ребра до основи;
двогранним кутом при ребрі основи і плоским кутом при вершині;
кутом нахилу бічного ребра до основи і плоским кутом при вершині.

Перший учень у парі читає один пункт, пояснює, узагальнює, а другий ставить питання. Другий пункт читає, пояснює й узагальнює другий учень, а перший ставить запитання. Це дозволить проявити учням більше ініціативи у процесі власного навчання та навчання один одного.

Завдання. Опрацювати в парах питання «Перетворення графіків функції»

Перетворення вздовж осі ординат
1. пара – у= f(x) +b
2. пара – у= k f(x)
3. пара – у=| f(x)|
Перетворення вздовж осі абсцис
1. пара – у= f(x+а)
2. пара – у= f(nx)
3. пара – у= f(|x|)

МЕТОД «СХЕМА ВЕННА»

Завдання: представити схематично у вигляді схеми Венна співвідношення між поняттями ромб, прямокутник, паралелограм, квадрат.

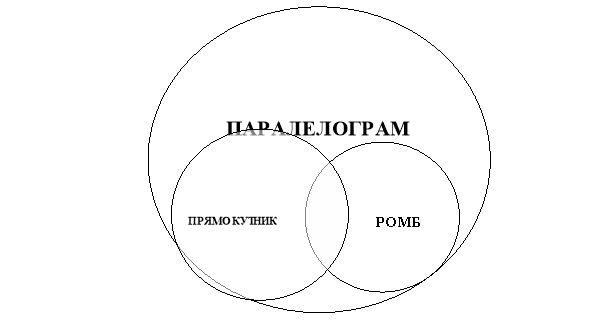
МЕТОД Т-СХЕМА

Завдання. Порівняти та протиставити трикутник і прямокутник

прямокутник

трикутник

4 сторони

4 кути

4 вершини

2 висоти

2 діагоналі

Сума кутів 360º

3 сторони

3 кути

3 вершини

3 висоти

3 бісектриси

3 медіани

Сума кутів 180º

МЕТОД «ЗНАЮ – ХОЧУ ДІЗНАТИСЯ – ДІЗНАВСЯ»

Тема «Відношення. Основна властивість відношення»

Що знаємо?

Про що хочемо дізнатися?

Про що дізналися?

Як називаються числа при діленні

Яку частину від числа а становить число b

Основну властивість дробу

Що показує відношення двох чисел

Як обчислити, у скільки разів одне число більше за друге

Поняття про відношення

Означення відношення

Основну властивість відношення

Для знаходження відношення різнойменних величин необхідно вибирати нову спільну одиницю вимірювання величин

Як замінити відношення дробових чисел натуральними

МЕТОД «СЕМАНТИЧНИЙ АНАЛІЗ ОЗНАК»

Завдання. Закінчіть твердження: «Якщо у трикутнику є прямий кут, тоді….». Які висновки можна зробити, вияснивши, що трикутник має прямий кут?

Завдання. Накреслити таблицю семантичного аналізу ознак геометричних фігур

Кути	Гострі, тупі, прямі, розгорнуті, більші за розгорнуті,суміжні, вертикальні, внутрішні різносторонні, внутрішні односторонні, відповідні
Сторони (рівні )	Рівносторонній трикутник, квадрат, ромб
Прямі кути	Прямокутник, квадрат, прямокутний трикутник, прямокутна трапеція

Під семантичним аналізом тексту задачі розуміється процес прочитання завдачі з подальшим виділенням основних понять: умова, питання, відомі дані, невідомі. Передбачається, що в результаті здійснення семантичного аналізу учень усвідомлює і представляє собі ситуацію, дану в тексті задачі, і зуміє налагодити зв'язки між даними і невідомими.

Задача. Швидкість руху пішохода на 9 км/год менша за швидкість велосипедиста. Одну й ту саму відстань велосипедист проїхав за 2 год, а пішохід пройшов за 5 год. Знайдіть швидкість руху пішохода.

Позначення шуканих величин:

V (км/год) t (год) S (км)

Велосипедист (х+9) 2 2 (х+9)

Пішохід х 5 5х

Рівняння: 2(х+9)=5х.

Задача. Вершник долає відстань між двома селищами за 5 год, якщо рухається зі швидкістю 12 км/год. З якою швидкістю він має рухатись, щоб подолати відстань за 4 год?

Умова у вигляді таблиці:

V	t	S
12 км/год	5 год	? км
? км/год	4 год	?км

СХЕМА

12 км/год

5 год

? км/год

4 год

Задача. Спочатку товар коштував 180 гр. Через деякий час його ціну підвищили на 20%, а потім знизили на 10%. Якою стала ціна товару після цих двох переоцінок?

І ціна - 180грн

Ціна після підвищення - ? грн, на 20% більше

Ціна після зниження - ? грн, на 10% менше

СХЕМА

І ціна

180 грн. 20%

ІІ ціна

10 %

ІІІ ціна

ПРИЙОМ КЛАСТЕР

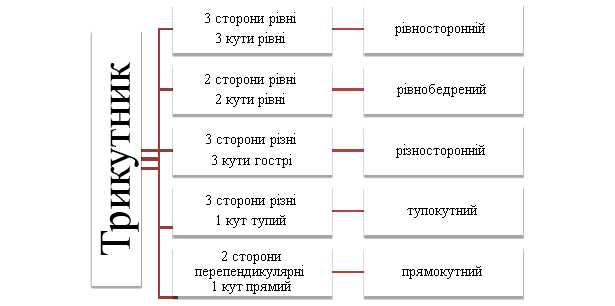
Завдання: Скласти кластер з ключовим поняттям «трикутник».

Проведіть класифікацію поняття «трикутник», беручи до уваги одночасно дві ознаки: порівняльну довжину сторін і градусну міру кутів.

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

Державний стандарт базової середньої освіти : постанова Кабінету Міністрів України від 30 вересня 2020 р., № 898
Кроуфорд А., Саул В., Метьюз С., Макінстер Д. Технології розвитку критичного мислення учнів / Наук. ред., передм. О.І. Пометун. – К.: Плеяди, 2006. – 220с.
Ліпман М. Чим може бути критичне мислення / Метью Ліпман // Вісник програм шкільних обмінів. – 2006. – № 27. – С. 17-23.
Макаренко В. М. Технологія формування та розвитку критичного мислення // Математика в школах України. – 2007. – № 26. – С. 2–10.
Мерзляк А.Г., Полонський В.Б., Якір М.С. Алгебра(підручник) 9 клас. – Х:, «Гімназія». 2010 – 320 с.
Мерзляк А.Г., Номіровський Д.А., Полонський В.Б., Якір М.С. Алгебра і початки аналізу: підручник для 10 (академічний рівень). - Х:, «Гімназія». 2010 – 320 с.
Наволокова Н. П. Енциклопедія педагогічних технологій та інновацій. – Х.: Вид. група «Основа», 2009. – 176 с.
Слєпкань З.І. Методика навчання математики: Підручник для студентів математичних спеціальностей педагогічних навчальних закладів. – Київ: Зодіак-ЕКО, 2000. – 512 с.
Стіл Дж., Мередит К., Темпл Ч. Методична система “Розвиток критичного мислення у навчанні різних предметів” (Підготовлено для проекту “Читання та письмо для розвитку критичного мислення”) / Посібники I-VIII. – Науково-методичний центр розвитку критичного та образного мислення “Інтелект”, 1998.
Тягло О. В. Критичне мислення: навч. посіб. [Текст] / О. В. Тягло. – Х.: Вид. група «Основа», 2008. – 189 с.
Тягло О. Післямова до статей Метью Ліпмана і Марка Вайнстейна / О. Тягло // Вісник програм шкільних обмінів. – 2006. – № 27. – C. 26-27.
Урок математики в сучасних технологіях: теорія і практика: Розвиток критичного мислення: Навч. – метод. посібник / Упоряд. І.С. Маркова – Х.: Вид. група «Основа». 2007 – 125с.
Шарко В.Д. Сучасний урок: технологічний аспект: Посібник для вчителів і студентів. – К.: СПД Богданова А.М., 2007.

docx

Завантажити

Зберегти на потім

Додав(-ла)

Кухаревич Варвара

Пов’язані теми

Математика, Методичні рекомендації

Додано

15 лютого 2023

Переглядів

5748

Оцінка розробки

Відгуки відсутні