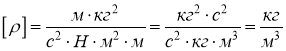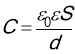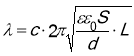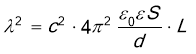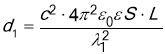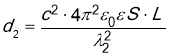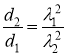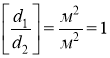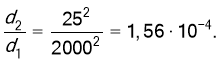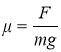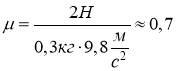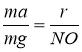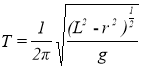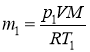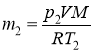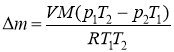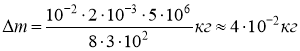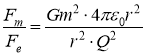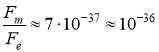МЕТОДИ РОЗВ’ЯЗУВАННЯ ФІЗИЧНИХ ЗАДАЧ

 

 

 

 

 

 

МЕТОДИ РОЗВ’ЯЗУВАННЯ ФІЗИЧНИХ ЗАДАЧ

ТВОРЧА РОБОТА ВЧИТЕЛЯ ФІЗИКИ

ЩАБЕЛЬНИК М.Г.

 

 

 

 

 

 

 

 

 

 

Аналітичний метод. Розв’язувати задачу починають з її запитання. Проаналізувавши умову, з’ясовують, за допомогою яких закономірностей можна визначити шукану величину. Але знайдене співвідношення, зазвичай, містить проміжні невідомі величини. Їх знаходять з інших закономірностей до тих пір, доки шукана величина не буде повністю виражена через відомі.

Розрахункова формула одержується як синтез окремих закономірностей.

Синтетичний метод. На противагу аналітичному методу, при розв’язуванні фізичної задачі встановлюють проміжні залежності між заданими фізичними величинами, частина з яких може бути зайвою. У результаті такого пошуку знаходять рівняння, яке пов’язує шукану величину з відомими. Отже, на відміну від аналітичного методу, де починають з шуканої величини, в синтетичному методі починають з величин, заданих в умові задачі.

У чистому вигляді аналітичний і синтетичний, як окремі, методи майже не застосовуються. При розв'язуванні задач використовують, як правило, і аналіз і синтез, тобто застосовують аналітико-синтетичний метод.

Аналітико-синтетичний метод — основний метод розв’язування задач з фізики в середній школі. Вдале застосування його в навчальному процесі дозволяє  відшукувати розв’язки задач, сприяє розвитку логічного  мислення учнів.

При цьому методі рішення шляхом аналізу, починаючи з питання завдання, з'ясовують, що треба знати для її вирішення, і, поступово розчленовуючи складну задачу на ряд простих, доходять до відомих величин, даних в умові. Потім за допомогою синтезу міркування проводять в зворотному порядку: використовуючи відомі величини, і підбираючи необхідні співвідношення, виробляють ряд дій, в результаті яких знаходять невідоме.

Задача.

Знайдіть тиск на грунт гусеничного трактора масою 10 т, якщо довжина опорної частини гусениці 2 м, а ширина 50 см.

Аналіз: Щоб визначити тиск трактора на грунт, треба знайти діючу на нього силу тяжіння, і площу опори. Сила тяжіння в задачі не дана, площа опори не вказана. Для визначення загальної площі опори, тобто площі опорної частини двох гусениць, треба дізнатися площу опори однієї гусениці і помножити її на два. Площу однієї   гусениці можна визначити, тому що відомі її ширина і довжина. Силу тяжіння, що діє на трактор, можна знайти за відомою його масою.

  Синтез: Міркування ведуть у зворотному порядку, в його ході складають план рішення і роблять необхідні обчислення. Послідовність міркування приблизно наступна. Знаючи ширину і довжину опорної частини гусениці, можна визначити опорну площу однієї гусениці. Для цього треба довжину помножити на ширину. Знаючи опорну площу однієї гусениці, можна визначити загальну площу опори трактора. Для цього треба знайдену площу, тобто площу опорної частини однієї гусениці, помножити на два. Знаючи масу трактора, знаходять силу тяжіння, що діє на нього. За силою тяжіння і площею опори можна визначити тиск трактора на грунт. Для цього силу тяжіння треба розділити на площу опори.

 

      Алгоритм розв’язування задач аналітико-синтетичним методом:

1. Вивчити умову задачі і записати її згідно з прийнятою символікою.

2. Перевести всі дані задачі в СІ.
3. Зробити в разі необхідності рисунок до розв’язку задачі.
4. Проаналізувати  умову задачі, в ході чого з'ясувати її фізичну суть, тобто з'ясувати фізичні явища, процеси і стани системи та відновити в пам'яті учнів фізичні закони та формули, які потрібні для розв'язку задачі;
5. Виявити, яких даних не вистачає в задачі і знайти їх у таблицях або довідниках.
6. Використовуючи відомі закономірності та формули, розв’язати задачу в загальному вигляді.
7. Установити чи перевірити одиниці певних величин.
8. Обчислити шукану величину.
9. Записати відповідь і проаналізувати її реальність, відповідність умові задачі.

 

Задача 1. Діаметр планети Уран становить 51000км, прискорення вільного падіння на його поверхні дорівнює 8,9м/с². Визначте середню густину цієї планети.

 

Дано: d = 51000км g =8,9 м/с2 G= 6,67∙10-11Н∙м2/кг2   ρ - ?	СІ d = 5,1∙107м	Розв’язання За означенням густини , де  M – маса Урана; V – його об’єм. Прискорення вільного падіння визначається за формулою
Отже, маса Урана дорівнює: Вважаючи Уран кулею, знайдемо його об’єм за формулою Підставимо отримані вирази у формулу для густини, отримаємо: . Перевіримо одиниці та визначимо числове значення шуканої величини:   = 1250 кг/м3. Відповідь: густина планети Уран становить  = 1250 кг/м3.

 

Задача 2. Радіоприймач можна настроювати на прийом радіохвиль від 25 до 2000м. Що треба зробити для прийому більш довгих хвиль – зближати чи розсовувати пластини конденсатора коливального контура?

Дано: S =const λ1 =25 м λ2 =2000м с=3 ∙108  м/с    - ?	Розв’язання Довжина радіохвиль залежить від періоду власних коливань контура:  , де с – швидкість поширення електромагнітних хвиль в середовищі. Період  власних коливань контура визначається за формулою: , де С – ємність конденсатора, L – ємність котушки.
Отже, . Ємність плоского конденсатора визначається  за формулою довжина хвилі залежить від відстані між пластинами d: . Виразимо d: . Запишемо цю формулу для двох випадків: , . Обчислення: Відповідь: , тобто пластини треба зблизити, оскільки .

 

 Метод  моделювання. Цей метод вважають змістовним «ядром» методів розв’язування задач, оскільки він супроводжує їх від самого початку (умови задачі, де вихідною моделлю є ілюстрація фізичної ситуації) до отримання відповіді. При розв’язуванні фізичних задач, зазвичай, використовують декілька методів, і тому метод моделювання поряд з застосуванням його як загальнонаукового, використовують інколи як спосіб або засіб.

Вибір системи відліку. Для опису будь-якого руху обов’язково вибирають систему відліку. Розрізняють інерціальні системи відліку (ІСВ), відносно яких усі тіла за відсутності дії на них сил або у випадку рівності нулю рівнодійної сили, рухаються рівномірно й прямолінійно або залишаються в стані спокою, та  неінерціальні системи відліку (НІСВ), які рухаються з прискоренням відносно інерціальних систем відліку. Вдалий вибір системи відліку дає можливість суттєво спростити розв’язок задачі.

     Алгоритм розв’язування  задач, розв’язання яких залежить від вибору системи відліку:

1. Вивчити умову задачі і записати її згідно з прийнятою символікою.

      2. Перевести всі дані задачі в СІ.

3. Вибрати систему відліку, яка складається із тіла відліку, пов'язаної з ним системи координат і початку відліку часу;

4. Виконуючи рисунок до задачі, потрібно зобразити систему відліку;

 траєкторію руху, всі векторні величини, що визначаються умовою і положенням тіла в початковий момент часу;

5. Скласти кінематичні рівняння (закони) руху для кожного тіла у векторній формі і в проекціях на вибрані осі координат;

6. У разі потреби встановити додаткові рівняння, які можуть виражати конкретні математичні зв'язки, що випливають з умови задачі;

7. Отриману систему рівнянь розв'язати відносно шуканих величин в загальному вигляді.

8.  Розрахувати числові значення певної величини.

7.  Записати відповідь і проаналізувати її реальність, відповідність умові задачі.                     

Задача 1. Ескалатор метро піднімає пасажира, що стоїть нерухомо на ньому, протягом 1 хв. По нерухомому ескалатору пасажир піднімається пішки протягом 3 хв. Скільки часу витратить пасажир на підйом пішки по ескалатору, який рухається?

Дано: СІ: Розв’язування:

t₁=3хв t₁=180с    v=v₁+v₂ - швидкість пасажира в системі відліку

t₂=3хв t₂=60с           «Земля»;

   t – ?                      v₁ – швидкість руху пасажира по ескалатору,

v₂ – швидкість ескалатора.

                                      Для даної системи відліку маємо рівняння:

                                              S= v₁ t₁             (1)

                                              S= v₂ t₂             (2)

                                              S= (v₁₊ v₂) t_.      (3)

Виразимо  t  із   (3):

           
 

де    
 

                                   ==.

Обчислення:

[t]==с,      t=

Відповідь: t=45с.

     Задача 2. Рибалка плив за течією річки і, пропливаючи під мостом, згубив запасне весло. Через годину він помітив утрату і, повер­нувшись назад, зустрів весло на 6 км нижче від моста. Яка швидкість течії річки, якщо рибалка, рухаючись за і проти течії, докладав однакових зусиль?

Дано:                            Розв’язування:

S=6км У системі відліку «Вода» весло нерухоме, оскільки його несе зі

t=1год     швидкістю течії відносно Землі. Значить, наскільки човен

 v_теч=?     віддаляється від весла, настільки ж він до нього і 

               наближається. Тому час руху човна до зустрічі з веслом

.

    Для визначення швидкості течії переходимо в систему відліку «Земля». У цій системі відліку весло переміщується на 6км за 2год. Звідси визначається швидкість течії як швидкість весла відносно Землі.

 

 v_теч=.

 

Обчислення:

[v]=км/год.

v_теч=6/2=3.

           Відповідь: v_теч=6/2=3км/год.

 

Графічний метод. Графічний метод у фізиці передбачає використання графіків для опису й пояснення природних процесів та закономірностей. Використання графіків сприяє наочному та більш глибокому розумінню фізичного процесу, навчає учнів виражати функціональну залежність аналітично, дає можливість уявити поставлену задачу, а також її розв’язок.

Графічне зображення законів прямолінійного руху і аналіз графіків мають за мету:

• навчити визначати характер руху та числові значення шляху, переміщення, швидкості й прискорення за графіком;
• наочно зображати функціональні залежності кінематичних величин;
• порівнювати графіки рухів, за якими можуть бути визначені кінематичні величини;
• навчити розв’язувати задачі на зустрічні рухи тіл (визначити час зустрічі, місце зустрічі, швидкість у момент зустрічі і т. д.

Задача1.

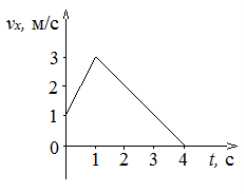
 За графіком швидкості рівноприскореного прямолінійного руху побудувати графік прискорення a_x= a_x(t).

                      ,

                     

                     (рух прискорений);

                      

                       (рух уповільнений).

         Побудуємо графік прискорення (рис.1 а, б).

 

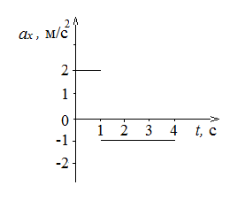
Задача2. З Харкова на захід вирушив велосипедист зі швидкістю 20 км/год, а через 3 год у тому самому напрямку виїхав автомобіль зі швидкістю 80км/год. Через який час після виїзду велосипедиста і на якій відстані від Харкова автомобіліст наздожене велосипедиста?

Дано:                                                Розв’язування

v₁ = 20 км/год          Розв’яжемо задачу графічним методом. Запишемо

v₂ = 80 км/год     рівняння руху велосипедиста й автомобіля:

τ = 3 год                                 x₁ = 20t, x₂ = 80 (t – 3).

T – ?, x – ?                  Побудуємо їхні графіки. Точка перетину графіків визна –

чатиме координату місця, де автомобіль наздожене велосипедиста, і час, коли це станеться.

 

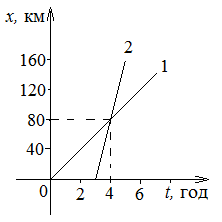
 Відповідь: автомобіль наздожене велосипедиста через

 t = 4 год після виїзду велосипедиста на відстані x = 80 км від Харкова.

Векторно-координатний спосіб розв’язування задач. Цей спосіб вважають основним алгоритмом розв’язування задач з динаміки. Виконують малюнок, на якому позначають всі сили, що діють на тіло, записують другий закон Ньютона у векторній формі, вибирають систему відліку, проектують сили на координатні осі й шукають невідому величину через систему отриманих рівнянь.

     Алгоритм розв’язування задач з динаміки векторно-координатним способом.

1. Прочитайте умову задачі.

2. Виясніть основне запитання задачі.

3. Зробіть скорочений запис умови задачі.

4. Виконайте малюнок, зобразивши на ньому взаємодіючі тіла.

5. Визначте, з якими тілами взаємодіє тіло, рух якого розглядається в 

          задачі.

6. Позначте на малюнку сили, що діють на тіло, рух якого розглядається,

          а також вектори швидкості і прискорення.

7. Запишіть у векторній формі рівняння руху тіла.

8. Виберіть найбільш раціональну для розв’язування систему відліку.

9. Запишіть рівняння руху в проекціях на осі координат.

10. Запишіть додаткові рівняння кінематики (якщо в цьому є необхідність)

          на основі аналізу умови задачі.

11. Розв’яжіть рівняння.

13. Підставте числові дані в результуючу формулу і виконайте обчислення

 

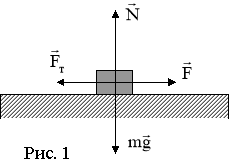
Задача 1. На ділянці дороги, де встановлений дорожній знак водій застосував аварійне гальмування. Інспектор ДАІ по сліду коліс виявив, що гальмівний шлях дорівнює 12 м. Чи порушив водій правила дорожнього руху, якщо коефіцієнт опору руху дорівнює 0,6?

 

 

Дано:                                                           Розв’язування

v₀ = 30км/год = 8,3 м/с       Оскільки автомобіль гальмує, то рух уповільнений,

v = 0 м/с                         кінцева швидкість дорівнює нулю.

μ = 0,6                               Тоді гальмівний шлях дорівнює

S_{гальм. max} =12 м                             .

S_гальм. = ?                     

Для знаходження гальмівного шляху необхідно знайти модуль прискорення. Його можна визначити, застосовуючи основне рівняння динаміки:

,

OX: , .

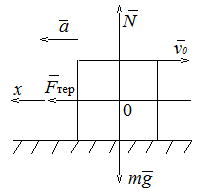Оскільки поверхня горизонтальна, то , . Тоді , .

Підставимо прискорення в значення гальмівного шляху:

.

                

 

Обчислення:

,

Відповідь: S_гальм. =5,7 м при швидкості 30 км/год. Але гальмівний шлях автомобіля 12 м, значить, його початкова швидкість була більшою за дану, тобто водій порушував правила дорожнього руху.

 

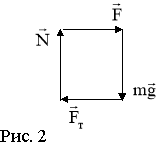
Задача 2. З яким прискоренням а ковзає брусок по похилій площині з кутом нахилу α =30⁰ при коефіцієнті тертя μ = 0,2?

Дано:                                              Розв’язування

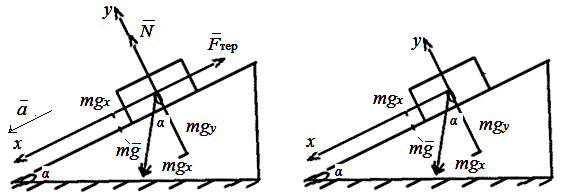
α =30⁰              Вивчивши умову задачі, побудуємо рисунок.

μ = 0,2             Вважаємо, що брусок рухається прямолінійно і

а– ?         рівноприскорено. Зобразимо сили, що діють на брусок, враховуючи, що прискорення спів напрямлене з рівнодіючою силою.

Згідно з другим законом Ньютона .

                         а                                                           б

Розпишемо рівнодіючу силу як геометричну суму сил, що діють на тіло:

.

Оберемо вісь для проектування, співпадаючу з напрямом прискорення і запишемо рівняння (1) у вигляді проекцій на вісі OX і OY

OX:

OY:

Розпишемо проекції, приділивши особливу увагу проекціям і .

За визначенням

, ,

тобто

.

Визначимо знак цих проекцій:

.

Проекція від’ємна, оскільки кут, створений і віссю OY, більший за 90⁰ (рис.б).

OX:

OY:

Із проекції на вісь OY   .

Визначимо силу тертя і підставимо її значення в формулу прискорення

         ,

.

Обчислення:

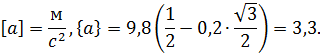
Відповідь: а = 3,3м/с².

 

Задача3. На горизонтальній поверхні стола лежить брусок. Під яким кутом до горизонту потрібно прикладати силу до бруска, щоб він рухався рівномірно, а модуль цієї сили був найменшим? Коефіцієнт тертя ковзання між поверхнею стола і бруском дорівнює μ.

Відповідно до даного алгоритму учні виконують малюнок, на якому позначають вектори сил, що діють на брусок (рис. 1). Записують другий закон Ньютона у векторній формі:               . (1)

Вибирають систему координат; записують векторне рівняння (1) в проекціях на координатні осі.

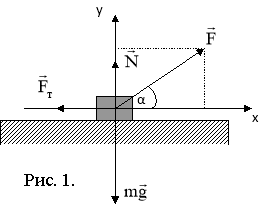На вісь х: . (2)

 На вісь y:   . (3)

Актуалізується формула для сили тертя ковзання: . (4)

Розв’язавши систему рівнянь (2-4), учні отримують формулу, яка виражає залежність сили F від кута :

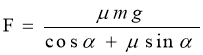    (5)

Наступний етап передбачає розв’язування підзадачі, яку можна сформулювати у вигляді запитання:

 Яким має бути кут α, щоб значення виразу   було максимальним?

 Ця підзадача для учня 9-го класу є творчою, а отже, основна задача також є творчою. Тут можливі декілька варіантів розв’язку.

Варіант 1. Знаходження точки екстремуму для функції,  шляхом диференціювання.

      Але цей варіант у 9-му класі є неприйнятним.

Варіант 2. Нехай , тоді , тоді  . Помноживши на cos β, отримаємо:

Цей вираз буде набувати максимального значення при тому ж самому куті α, що і вираз . Максимальне значення  коли  . Отже, tg  = , а  = arctg .

Варіант 3. Відмовитися від стереотипного підходу щодо розв’язку задачі і спробувати розв’язати задачу векторно-геометричним способом.

 Нормативна модель розв’язку:

  Запишемо рівняння (1) так: , де   (рис. 2). 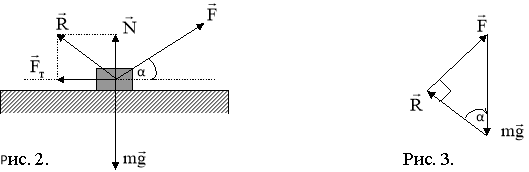Якщо Якщо сума трьох векторів дорівнює нулю, то вони мають утворювати трикутник (рис. 3). Модуль вектора  буде найменшим, коли цей вектор буде перпендикулярний до вектора . Тоді кут між векторами   і   (рис. 2) буде рівний шуканому куту α. А отже,,  = arctg .

 

Векторно-геометричний спосіб розв’язування задач. Значну частину задач як з механіки, так і з інших розділів фізики (електростатики, геометричної оптики) можна розв’язувати, використовуючи  векторно-геометричний спосіб. Суть його полягає в тому, що перехід «від векторних рівнянь до скалярних здійснюється на основі застосування знань з геометрії: правил додавання векторів, властивостей геометричних фігур, співвідношень між сторонами і кутами в прямокутному трикутнику, теореми Піфагора, ознак подібності й рівності трикутників, теореми косинусів і синусів тощо».

Алгоритм розв’язування задач векторно-геометричним методом:

1. Виконати малюнок, де зазначити усі сили, що діють на тіло;
2. Записати ІІ закон Ньютона у векторній формі
3. Виконати дії над векторами, використовуючи правила їх додавання;
4. Перейти до скалярних величин, використовуючи властивості геометричних фігур;
5. Отримати невідому величину.

 

Задача 1. Брусок, маса якого 300 г, рухається рівномірно по горизонтальній поверхні стола під дією горизонтально спрямованої сили, модуль якої дорівнює 2 Н. Визначити коефіцієнт тертя ковзання.

 

Дано: m=300 г = 0,3 кг F= 2H   μ - ?	Розв’язання 1. Зобразимо вектори сил, що діють на брусок (рис. 1). 2. Запишемо другий закон Ньютона у векторній формі: (1.1). 3. Виконаємо дії над векторами, скориставшись правилами додавання векторів. Так як їх сума рівна
нулю, то при додаванні ці вектори утворюють прямокутник (рис. 2). Врахуємо те, що довжина вектора, зображеного на малюнку, пропорційна модулю відповідної векторної величини.
Тоді, на основі властивості прямокутника про рівність його протилежних сторін, можна написати такі рівняння:; . Доповнивши їх формулою для сили тертя ковзання , отримаємо: .  Звідки . Обчислимо коефіцієнт тертя:  . Відповідь: µ=0,7.

 

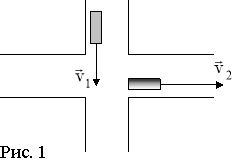
Задача2. Два автомобілі на перехресті рухаються у взаємно перпендикулярних напрямках з швидкостями відповідно v₁= 3 м/c і v₂= 4 м/c.

Знайти швидкість першого автомобіля відносно другого.

Дано: v1 = 3 м/c v2 = 4 м/c   v12 - ?	Розв’язання   Зробимо малюнок, на якому зобразимо ситуацію (рис. 1). Згідно з правилом додавання швидкостей: . Звідки .
Відкладемо вектори і з однієї точки і скористаємося правилом віднімання векторів. Отриманий векторний трикутник (рис. 2) є прямокутним.      Скориставшись теоремою Піфагора, можна записати, чому дорівнює модуль відносної швидкості: .       Виконаємо розрахунки: . Відповідь: v12= 5м/с

             

Задача 3. Кулька, підвішена на нитці, рівномірно обертається у горизонтальній площині по колу, радіус якого 0,3 м. Довжина нитки 50 см. Знайти період обертання кульки.

Розв’язання:

Дано: r= 0,3 м L= 50 см =0,5м   T  - ?

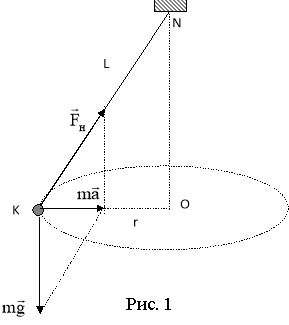
1. Зобразимо на малюнку вектори усіх сил, що діють на кульку (рис. 1). 2. Запишемо другий закон Ньютона: . Вектор рівнодійної сили лежить у площині кола і спрямований до центру. Трикутник,

утворений векторами та , подібний трикутнику КNO (ознака подібності трикутників за двома кутами). 3. На основі подібності трикутників можна записати таку рівність: . Так як , то .          (1) Модуль доцентрового прискорення .               (2) Прирівнявши праві частини рівностей (1) (2), отримаємо: . Виконаємо розрахунки:                                        Т=0,03(с).      Відповідь:Т=0,03(с).

 

 

Метод оцінки. Оцінка фізичної величини полягає в розрахунку порядку самої величини (оцінка порядку) або в порівнянні однорідних величин за їх   порядком (порівняння за порядком). При розрахунку порядку фізичної величини всі складові, які визначають цю величину, записують у стандартному вигляді, а потім оцінюють порядок кожної з них. Орієнтуються за найвищим порядком. Якщо величина має порядок на дві одиниці нижче найвищого, то таку величину не беруть до уваги. Цей метод є основним при розв’язуванні задач-оцінок, значна частина яких вимагає від учнів не лише оцінити фізичну величину, а й самостійно задати числові значення параметрів, що описують цю ситуацію.

Алгоритм розв’язування задач методом оцінки.

1. Прочитайте умову задачі.

2. Виясніть основне запитання задачі.

3. Зробіть скорочений запис умови задачі.

4. Заокругліть величини та запишіть їх в стандартному вигляді.

5. Знехтуйте величиною, яка має порядок на дві одиниці нижче найвищого.

6 Виконайте обчислення.

6. При порівнянні величин знайдіть їх відношення в загальному вигляді.

7.  Виконайте числовий розрахунок порядку цього відношення.

Задача1. Дано: V = 9 л М =210-3 кг/моль р1 = 52∙105 Па р2 = 5∙104 Па Т1 = 296 К Т2 = 283 К R=8,31 Дж/(мольК)   Оцініть порядок величини  m	СІ V  10-2 м3 М =210-3 кг/моль р1  5∙106 Па р2 = 5∙104 Па Т1 = 3∙102 К Т2 = 3∙102 К R8Дж/(мольК)	Розв’язання Запишемо рівняння стану ідеального газу для кожного із станів . Звідси , . . Так як Т1=Т2=Т, маємо .
Так як р2 значно менше р1 значенням р2 знехтуємо. Для оцінки порядку величини  m маємо .

При порівнянні фізичних величин, що залежать від інших величин, спочатку знаходять їх відношення у загальному вигляді, а потім приводять числовий розрахунок порядку цього відношення.

Задача2. Порівняти силу тяжіння F_т двох протонів та силу їх електричної взаємодії F_е.

Дано: G = 6,710-11 Нм2/кг2 m =1,6710-27 кг Q = 1,6∙10-19 Кл –?

Розв’язання Знайдемо відношення цих сил: . Після арифметичного розрахунку отримуємо:

 

Таким чином, сила тяжіння двох протонів на 36 порядків менша за силу їх електричного відштовхування (гравітаційна взаємодія надзвичайно мала по відношенню до електромагнітної взаємодії).

 

При розв’язуванні задач з статики доцільно показати на прикладі використання трикутника Стевіна: за умови рівноваги тіл, які знаходяться на похилих площинах, маси цих тіл відносяться як довжини похилих площин, що перетинаються горизонтальною лінією .

 

 

 

 

 

 

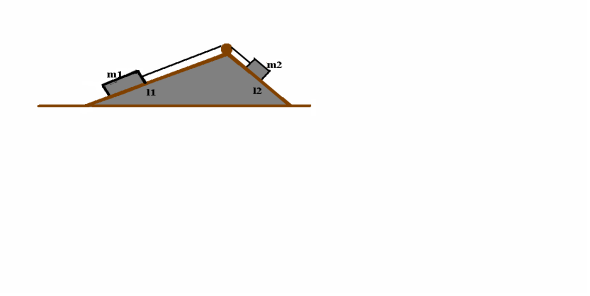
Стевін також встановив принцип додавання статичних сил: три сили, які діють на одну точку, перебувають у рівновазі за умови, коли вони паралельні й пропорційні трьом сторонам плоского трикутника.

Приклад розв’язування задач статики з використанням трикутника сил.

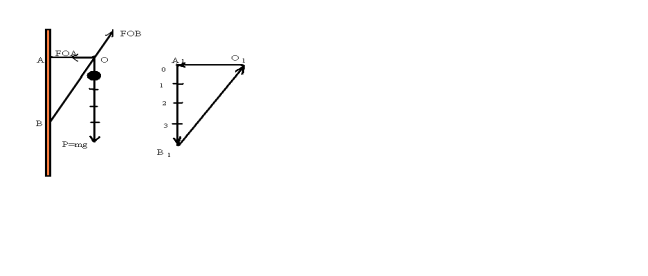Задача. На кронштейні висить лампа вагою 4Н. Знайти значення сил пружності, що виникають у деталях ОА і ОВ.

 

Дано:                                Розв’язання

F=4Н        Обираємо масштаб для побудови трикутника. Нехай 1см на

 Fпр-?    малюнку відповідає силі 1Н. Відповідно до вказівок Стевіна

               будуємо сторону трикутника А₁В₁, довжина якої відома: 

               4см=4Н. Ця сторона трикутника паралельна напрямку дії сили

              тяжіння на лампу. З точки А₁ проводимо лінію, паралельну до напрямку дії сили в деталі ОА, а потім з точки В₁ – паралельну напрямку дії сили в  деталі ОВ. На перетині побудованих ліній буде точка О₁. Одержали замкнений трикутник сил відповідно до рекомендацій Стевіна. Знаючи обраний масштаб за допомогою лінійки вимірюємо значення сили пружності в деталі ОА (О₁А₁) і сили реакції (також сили пружності) з боку деталі ОВ (О₁В₁). Задача розв’язана.

 

Метод можливих переміщень (метод Лагранжа). За цим методом для рівноваги механічної системи з ідеальними зв’язками необхідно й достатньо, щоб сума робіт усіх прикладених до системи активних сил на будь-якому з можливих переміщень системи дорівнювала нулю. Сили реакції при цьому не враховуються. При необхідності знаходження таких сил потрібно відкинути той зв’язок, силу реакції якого визначають.

Перевагою використання рівнянь Лагранжа другого роду до вирішення задач динаміки є єдина методика вирішення задач.

 

Алгоритм роз в’язання задач за допомогою рівнянь Лагранжа другого роду.

1. Визначаємо кількість ступенів вільності системи та вибираємо узагальнені координати.

2. Знаходимо узагальнені сили за правилом, описаним у 3.4 б.

3. Визначаємо кінетичну енергію системи як функцію узагальнених координат і узагальнених швидкостей.

4. Знайдені величини підставляємо у (3.24), отримуємо рівняння Лагранжа другого роду.

5. Спрощуємо та інтегруємо рівняння Лагранжа другого роду.

6. Визначаємо сталі інтегрування із початкових умов задачі.

7. Знаходимо закон руху точок системи.

8. За найденим законом визначаємо реакції зв’язків.

9. Проводимо аналіз результатів обчислень.

 

Найзагальніші методи розв’язування задач механіки ґрунтуються на загальному принципі аналітичної статики, який називається принципом можливих переміщень, або принципом Лагранжа. Об’єднавши його з відомим принципом Даламбера, Лагранж дістав загальне рівняння динаміки, з якого як наслідок випливають основні диференціальні рівняння руху системи.

Принцип можливих переміщень є наслідком визначення можливих переміщень і деяких властивостей звв’язків.

Принцип можливих переміщень

Якщо система матеріальних точок з ідеальними зв’язками перебуває в рівновазі, то сума робіт активних сил, прикладених до точок системи, на можливих переміщеннях або дорівнює нулю, або від’ємна .

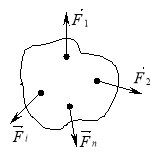
        Розглянемо систему n точок (рис.3.6) з ідеальними зв’язками, яка перебуває в рівновазі. У рівновазі перебуває і кожна точка системи. Тому, користуючись аксіомою про звільнення від зв’язків, маємо

 ; (a)

де - рівнодійна активних сил, прикладених до - тої точки системи; рівнодійна реакцій ідеальних зв’язків, прикладених до цієї самої точки.

Надамо точкам системи можливих переміщень і обчислимо роботу, яку виконують активні сили і реакції зв’язків на цих переміщеннях:

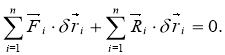                    (b)

 

Користуючись умовою (4.1) , дістаємо

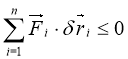       .                (3.4)

Знак нерівності відповідає, як і раніше, наявності серед зв’язків нестримуючих. Довели необхідність виконання умови (3.4) для рівноваги системи. Доведемо її достатність.

Припустимо, що система зі стану рівноваги починає рухатися. За теоремою про зміну кінетичної енергії системи робота, виконана діючими на систему силами, на дійсних переміщеннях додатна. Вважатимемо зв’язки, накладені на точки системи, стаціонарними. Тоді дійсні переміщення збігаються  з одним із можливих. Отже, це і буде робота, яку виконують активні сили на можливих переміщеннях. Але це твердження суперечить умові (3.4), тобто невірне.

Принцип повністю доведено.

Умовимося розглядати тільки такі можливі переміщення, які не звільняють систему від зв’язків. Співвідношення (3.4) набуває вигляду

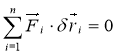                                                                 (3.5)

і називається загальним рівнянням статики. Цей термін можна пояснити тим, що з нього легко дістати умови рівноваги вільного твердого тіла і всі можливі умови рівноваги системи тіл.

рис. 3.7

Розглянемо вільне тверде тіло (рис.3.7), на яке діють сили . Якщо тіло невільне, скористаємось аксіомою про звільнення від зв’язків і реакції зв’язків приєднаємо до активних сил.

Надамо тілу певного можливого переміщення і обчислимо елементарну роботу всіх діючих сил на цьому переміщенні. Згідно з теоремою про роботу сил, що діють на абсолютно тверде тіло, ця робота дорівнює роботі, виконаній головним вектором системи сил на переміщенні полюса, і роботі головного моменту  відносно полюса на обертальному переміщенні навколо полюса:

                                                      (c)

Полюс беремо в довільній точці О. На підставі (3.5) вираз (c) набуває вигляду

                                                         (d)

Можливе переміщення полюса і обертальне переміщення навколо полюса - незалежні. Нехай =0, .

Тоді з (m) маємо .

Ця умова здійснюється для всіх довільних лише тоді, коли

 .                  (e)

Аналогічно можна довести , що                                     (f)

                           

Рівності (e) та (f) – відомі умови рівноваги вільного твердого тіла.

Аналогічно можна знайти умови рівноваги невільного твердого тіла. Розглянемо, наприклад, тверде тіло, що має дві нерухомі точки, нерухому вісь. Візьмемо полюс на цій осі. Тоді =0, а , де - орт осі обертання.

Рівняння (d) набуває вигляду

                             .                                       (g)

Співвідношення (g) повинно бути справедливим при довільному . Отже,

                                                                (h)

Рівність (h) – відома умова рівноваги тіла з нерухомою віссю.

Розв’яжемо попередню задачу методом можливих переміщень. Нехай необхідно визначити силу, що виникає в деталі ОА. Відкинемо цей  зв’язок. Тобто вантаж уже не утримується поперечною балкою ОА. Покажемо замість зв’язку силу реакції F_ОА. Тепер нова система може обертатися навколо осі, що проходить через точку В, перпендикулярно до площини малюнка.

Здійснимо нескінченно мале уявне переміщення Δs навколо осі за годинниковою стрілкою і підрахуємо суму робіт обох сил на цьому переміщенні: .

Звідки

Вимірявши кути α₁та α₂  та знаючи силу Р, одержуємо значення шуканої сили F_ОА.

При визначенні кутів слід обрати зручний спосіб їх відліку, наприклад, від напрямку можливого переміщення Δs до напрямку дії сили проти годинникової стрілки.                                                       

Щоб визначити силу реакції Δs, відкинемо зв’язок ОВ, замінивши його відповідною силою реакції. Виконаємо уявне нескінченно мале переміщення  Δs балки АО, яка обертається навколо осі, що проходить через точку А, за годинниковою стрілкою. Знаходимо суму робіт:

Звідси

 

 Метод розмірностей. Під розмірністю фізичної величини розуміють вираз, що відображає її зв’язок з основними величинами СІ, при коефіцієнті пропорційності рівному одиниці. Розмірності основних величин виражають через їх позначення. Наприклад, у механіці за одиниці виміру прийняті довжина, маса й час: dim(l) L, dim(m) M, dim(t) T, де dim – скорочення «dimension», тобто «розмірність». Будь-яку фізичну величину в механіці можна представити у вигляді Y=L^αM^βT^γ , де α,β,γ – показники розмірності фізичної величини. Якщо величина безрозмірна, то показник розмірності рівний нулю. Для використання цього методу при розв’язуванні фізичних задач дотримуються таких правил:

1. Розмірність довільної фізичної величини визначається добутком позначень основних величин, піднесених у відповідні степені.
2. Додавати та віднімати можна лише величини однакової розмірності.

Метод розмірностей є ефективним способом швидкого контролю правильності виведення формул при порівнянні розмірностей правої і лівої частин.

Приклад. Використовуючи метод розмінностей, вивести формулу кінетичної енергії матеріальної точки.

Відомо, що кінетична енергія матеріальної точки Е_к залежить від маси точки m та від модуля її швидкості v. Припустимо,що ця залежність нам не відома. Тоді залежність Е_к=f(m,v) можна записати у вигляді

Е_к=Am^xv^y   (1).

Виразимо фізичні величини, що входять до цієї формули, через основні одиниці

 

[Е_к]=1Н*м=1кг*м²    →ML²T^-2

  c²

[m]=1кг   →M

[V]=1 кг*м/с²    →LT^-1  

і підставимо у формулу (1).

 Метод розмірностей дає змогу знайти залежність між величинами з точністю до постійного множника.