ЗМІСТ

 

ВСТУП .............................................................................................................................. 2

        РОЗДІЛ      І.      НАУКОВО-ТЕОРИТИЧНІ      ОСНОВИ      ПОНЯТЬ      ЗАДАЧ

ПРИКЛАДНОГО ТА ПРАКТИЧНОГО ЗМІСТУ  ....................................................... 5

1.1 Історія використання прикладних та практичих задач при вивченні математики  ...................................................................................................................... 5

1.2 Науково-теоритичні основи понять задач прикладного та практичного змісту  6

РОЗДІЛ ІІ. ЗАСТОСУВАННЯ ЗАДАЧ ПРИКЛАДНОГО ТА ПРАКТИЧНОГО

ЗМІСТУ ПРИ ВИВЧЕННІ КУРСУ МАТЕМАТИКИ  ЯК ОДИН ІЗ ШЛЯХІВ ДО

ЯКІСНОЇ ОСВІТИ  .......................................................................................................... 9

2.1 Методичні аспекти використання прикладних та практичних задач при вивченні математики  ...................................................................................................... 9

2.2 Методичні аспекти використання прикладних та практичних задач при вивченні математики у 5-6 класах  .............................................................................. 11

РОЗДІЛ ІІІ. ЗАДАЧІ ПРИКЛАДНОГО ТА ПРАКТИЧНОГО ЗМІСТУ У

ВИВЧЕННІ МАТЕМАТИКИ 5 КЛАСУ  .................................................................... 16

3.1. Площина. Пряма. Промінь  ................................................................................... 16

3.2. Кут  ........................................................................................................................... 17

3.3. Площа прямокутника та квадрата  ....................................................................... 19

3.4. Об’єм прямокутного паралелепіпеда та куба  ..................................................... 21

РОЗДІЛ ІV. ЗАДАЧІ ПРИКЛАДНОГО ТА ПРАКТИЧНОГО ЗМІСТУ У

ВИВЧЕННІ МАТЕМАТИКИ 6 КЛАСУ  .................................................................... 25

4.1. Масштаб  ................................................................................................................. 25

4.2. Довжина кола. Площа круга  ................................................................................. 27

4.3. Кругові та стовпчасті діаграми  ............................................................................ 29

4.4. Координатна площина  .......................................................................................... 31

ВИСНОВКИ ................................................................................................................... 36

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ ..................................................................... 38

ДОДАТОК  ..................................................................................................................... 41

ВСТУП 

 

Освіта XXI століття - це освіта для людини, що має розвиваючу, культуротворчу домінанту: виховання відповідальної особистості, яка здатна до самоосвіти й саморозвитку, вміє критично мислити, опрацьовувати різноманітну інформацію, використовувати набуті знання і вміння для творчого розв'язання проблем, прагне змінити на краще своє життя і життя своєї країни. Школа має формувати компетентну особистість, здатну самостійно здобувати знання і застосовувати їх на практиці, грамотно опрацьовувати інформацію, бути комунікабельним, контактним у різних соціальних групах, самостійно працювати над розвитком власного інтелекту, культурного й морального рівня, критично та творчо мислити, генерувати нові ідеї, приймати рішення, планувати стратегію власного життя, швидко адаптуватися до будь-яких змін у навколишньому  середовищі. 

Державний стандарт базової та повної середньої освіти основною метою освітньої галузі “Математика” ставить формування в учнів математичної компетентності на рівні, достатньому для забезпечення життєдіяльності в сучасному світі, успішного оволодіння знаннями з інших освітніх галузей у процесі шкільного навчання, забезпечення інтелектуального розвитку учнів, розвитку їх уваги, пам’яті, логіки, культури мислення та інтуїції. [7]

Україна є учасником  програми  PISA - 2018. Міжнародні порівняльні дослідження стали невід’ємною частиною системи оцінювання якості освіти у багатьох країнах світу. Вони дозволяють об’єктивно оцінити стан освіти в державі, сформулювати пріоритетні напрямки і визначити фактори вдосконалення

галузі. [21]

У межах цієї Програми підлітки проходять тестування з математики, природничих наук і читання, а також відповідають на запитання під час анкетувань. Варто зазначити, що дослідження не перевіряє знань програмового матеріалу, натомість його завданням є визначити в учнів окремих країн здатність до використання знань і умінь з математики та природничих наук у життєвих ситуаціях, а також, яким рівнем читацької грамотності вони володіють.

Дослідження має на меті визначити, наскільки учень зможе використовувати знання й уміння, отримані в школі, за можливих життєвих труднощів і викликів, протистояти яким ці знання й уміння зможуть допомогти. Отже, PISA має на меті визначити, наскільки в учнів розвинена здатність до використання знань і умінь з математики у подоланні різноманітних життєвих викликів і проблем, пов’язаних із математикою.

Участь в PISA-2018 дозволить громадянам України, зокрема, спеціалістам у галузі освіти, об’єктивно оцінити стан середньої освіти в країні, усвідомити значущість поступових перетворень у цій сфері, політикам – приймати

обґрунтовані рішення про необхідність змін. [22] 

Зважаючи на сьогодення, усе частіше ми зустрічаємось із проблемою: учні втрачають інтерес до навчання, відсутня зовнішня мотивація, немає бажання здобувати знання. Виникло протиріччя між необхідністю забезпечити належну якість освіти в умовах динамічного розвитку науки й технологій та неможливістю розв’язати цю задачу традиційним шляхом. Тому перед нами, вчителями математики, поставлена проблема: в умовах становлення й розвитку високотехнологічного інформаційного суспільства в Україні виникає необхідність підвищення якості та пріоритетності шкільної математичної освіти,  включення математичних предметів до навчальних  планів  усіх  рівнів  освіти,  поліпшення математичної підготовки учнів. 

Реалізувати поставлені завдання можна за умови посилення практичної, прикладної та політехнічної спрямованості шкільного курсу математики. 

Відповідний рівень математичної підготовки досягається в процесі навчання, орієнтованого на широке розкриття зв'язків математики з навколишнім світом, із повсякденним життям та вирішенням певних життєвих проблем. Тому очевидна необхідність підсилення практичного, прикладного спрямування шкільної освіти, мотивації навчальної діяльності учнів. Отже,  застосування отриманих знань, умінь і навичок в процесі вирішення повсякденних життєвих проблем є життєвонеобхідним.

Саме тому, метою даної роботи є: 

•      теоретично обґрунтувати необхідність використання задач прикладного та практичного змісту з метою реалізації прикладної спрямованості  курсу математики 5-6 класу; 

•      з’ясувати можливості розширення спектру застосувань практичних задач;

•      довести, що необхідно збільшувати кількість прикладних та практичних задач у процесі вивчення математики;

•      продемонструвати на прикладах зразки рекомендованих задач;

•      показати перспективи застосування прикладного та практичного підходу в процесі вивчення математики.  

 

      

РОЗДІЛ І. НАУКОВО-ТЕОРИТИЧНІ ОСНОВИ ПОНЯТЬ ЗАДАЧ ПРИКЛАДНОГО ТА ПРАКТИЧНОГО ЗМІСТУ

 

 

1.1 Історія використання прикладних та практичних задач при

вивченні математики

 

Прикладна  й  практична  спрямованість  навчання - одна  зі  змістовнодидактичних  цілій  вивчення  предмету. Серед  найважливіших  дидактичних  принципів  навчання  сучасна  дидактика  на  першє  місце  ставить  принцип  зв’язку навчання з навколишнім середовищем. Видатний  педагог         Я.А. Коменський переконував, що  учень  легше  засвоюватиме  навчальний  матеріал,  якщо знатиме, яку користь у  повсякденному  житті   має  те, що  вивчається. Значне місце для задач прикладного змісту виділяв у своїй праці відомий вітчизняний педагог В.О. Сухомлинський. Сутність його роздумів зводиться до вивчення та аналізу процесу розв’язання дітьми задач такого типу.

Про роботу в  цьому напрямку він так пише у своїй книзі «Серце віддаю дітям»:

        «В      оточуючому      світі      тисячі      задач.      Їх      придумав      народ,      вони

живуть  в  народній  творчості як  розповіді-загадки». Про зв’язок  знань  і  практичної  діяльності  висловився  й  відомий  німецький  педагог А.Дістервег: «Сумне  явище,  коли голови  учнів  наповнені  великою  чи  малою  кількістю  знань, але вони не навчились  їх  застосовувати».  Принципу  зв’язку  навчання  з  життям  на  початку  20  ст.  присвятив  свої  праці  й  вчений-практик  П.П.

Блонський.  Велике  значення  цьому  питанню  надавав  вчений  М.М. Пістряк.  Особливе  місце  він  відводив  практиці  розв’язання  проблеми  в  сільській  школі. На необхідність посилення  практичної  спрямованості  в навчанні математики ще з молодших класів указують сучасні провідні науковці  О.Я. Савченко,  А.М. Пишкало,  Н.О. Менчинська. Практика застосування  принципу  зв’язку  навчання  математики  з життям  широко і глибоко розроблена для середньої і старшої школи авторами шкільних підручників з математики О.С.Істером, А.Г.Мерзляком, В.Б.Полонським, М.С.Якіром, Н.А.Тарасенко.  

Показуючи  практичну й прикладну  спрямованість  шкільного  курсу  математики, великий  внесок  в розвиток  цієї  проблеми  зробили  вчені         П.Р. Атутов, В.Г. Зубов, М.М. Скаткін, С.М. Шабалов, О.О. Шибанов  та  інші. Усі  вони  наполягають на тому,  що в ході навчання  учень повинен  не  тільки  засвоїти  суму  знань, а й оволодіти способами  їх  застосування на  практиці, набути  широких  умінь  ефективного  використання математичних знань  у подальшій  трудовій  діяльності. Розв’язання  цих завдань, за їхнім глибоким  переконанням, значною  мірою  пов’язане  з  правильною  реалізацією  принципу зв’язку навчання  із життям. Важливість  застосування  дидактичного  принципу зв’язку  навчання  з  життям  у  забезпеченні  учнів  свідомими  й  міцними  знаннями  з  математики  висвітлено  у  Державному  стандарті  базової  та  повної  загальної  середньої  освіти, в  Державній  національній  програмі «Освіта», у методичних  рекомендаціях  МОН України  щодо  викладання  математики, у нових  навчальних  програмах  вивчення  математики.

Отже, шляхи  реалізації  прикладної  та  практичної  спрямованості  навчання  математики  є актуальними. В ході навчання  учень повинен  не  тільки  засвоїти  певні  знання, а й оволодіти способами  їх  застосування на  практиці, набути  широких  умінь  ефективного  використання математичних знань у повсякденному житті.

 

 

1.2 Науково-теоритичні основи понять задач прикладного та практичного змісту

 

У методиці навчання математики існують різні тлумачення поняття «прикладна спрямованість». Ю.М. Калягін і В.В. Пікан розрізняють поняття «прикладна» й «практична» спрямованість. На їх погляд «прикладна

спрямованість навчання математики – це орієнтація змісту і методів навчання на застосування математики в техніці і суміжних науках, у професійній діяльності, в народному господарстві і побуті». [14]

Прикладна спрямованість сприяє формуванню наукового світогляду й показує роль математики в сучасному виробництві, економіці, науці.  Практична спрямованість навчання математики – «це спрямованість змісту і методів навчання на розв'язування задач і вправ, на формування у школярів навичок самостійної діяльності математичного характеру».  У процесі навчання прикладна і практична спрямованість функціонують спільно. [14]

Інакше розуміє прикладну спрямованість В.А. Долінгер.  На його думку,  «прикладна спрямованість математичних знань повинна означати як їх практичне застосування, так і їх теоретичне значення в самій математиці. Лише в цьому випадку буде виховуватися в учнів справжня повага до сили наукових знань».

Прикладна спрямованість навчання математики найбільше реалізується при розв'язуванні прикладних задач. Що ж розуміти під поняттям «задача»? Г.П. Бевз [3] визначає математичну задачу будь-яку вимогу обчислити, побудувати, довести або дослідити що-небудь, що стосується просторових форм чи кількісних відношень, або запитання, рівносильне такій вимозі. Отже, задача – це будь-яка вимога обчислити, побудувати, довести щось. У шкільній практиці до задач у широкому розумінні відносять не лише текстові, сюжетні задачі, а й різного характеру вправи, приклади [9]. 

Під прикладними задачами в школі розуміють задачі, які виникають в повсякденному житті й розв'язуються математичними методами й способами, які визначаються в шкільному курсі. Сформулюємо основні вимоги до прикладних задач, які використовуються у навчанні математики. [6]

1.      Задачі повинні мати реальний практичний зміст, який забезпечує ілюстрацію практичної цінності і значущості набутих математичних знань. 

2.      Задачі повинні відповідати шкільним програмам і підручникам за формулюванням і змістом методів і фактів, які будуть використовувати в процесі їх розв'язування. 

3.      Задачі повинні бути сформульовані доступною і зрозумілою мовою, не містити термінів, з якими учні не зустрічалися і які вимагатимуть додаткових пояснень. 

4.      Числові дані в прикладних задачах повинні бути реальними, відповідати існуючим у практиці. 

5.      У змісті задачі по можливості повинен бути відображений особистий досвід учнів, місцевий матеріал, який дозволяє ефективно показати використання математичних знань і викликати в учнів пізнавальний інтерес.

6.      Прикладні задачі повинні відображати ситуації промислового і сільськогосподарського виробництва, економіки, торгівлі, екології, ілюструвати застосування математичних знань у конкретних професіях людей. Враховуючи політичну ситуацію в країні, варто особливу увагу приділити задачам патріотичного змісту, що може бути забезпеченням реалізації виховної мети на уроках математики.

7.      У прикладних задачах числові дані, як правило, наближені, а це означає, що при їх розв'язуванні необхідно використовувати обчислювальні засоби. 

8.      При розв'язанні прикладних задач у класах з поглибленим вивченням математики їх формулювання може бути розширене і становити собою деяке теоретичне зведення до проблеми, що вивчається. Сама проблема може мати багатоступеневе розв'язання, при якому кожний наступний етап розвиває й доповнює попередній. 

Таким чином, для реалізації прикладної спрямованості в навчанні математики велике значення має використання у викладанні різних форм організації навчального процесу. Завдання з практичним змістом - це математична задача, яка розкриває міжпредметні зв'язки і знайомить  зі сферами людської діяльності, у яких вона може застосовуватися. Прикладна задача може бути поставлена в будь-якій сфері людської діяльності. Так, як і завдання з практичним змістом, прикладна задача вирішується математичними засобами, опираючись при цьому на математичні правила і формули.

      

РОЗДІЛ ІІ. ЗАСТОСУВАННЯ ЗАДАЧ ПРИКЛАДНОГО ТА ПРАКТИЧНОГО ЗМІСТУ ПРИ ВИВЧЕННІ КУРСУ МАТЕМАТИКИ  ЯК ОДИН ІЗ ШЛЯХІВ ДО ЯКІСНОЇ ОСВІТИ

 

 

2.1 Методичні аспекти використання прикладних та практичних задач

при вивченні математики 

 

Прикладна спрямованість навчання математики формує в учнів розуміння математики  як методу пізнання та перетворення навколишнього світу, який має розглядатися не тільки областю застосувань математики та джерелом нових математичних ідей. Навчання математичного моделювання, застосування математичних знань до розв’язування задач прикладного змісту, що виникають поза межами математики й розв’язуються математичними методами, сприяє мотивації навчання, стимулює пізнавальні інтереси учнів. 

Практичне спрямування шкільного курсу математики передбачає формування в учнів умінь використовувати здобуті знання під час вивчення як самої математики, так і інших предметів. Політехнічне спрямування передбачає використання математичних знань для пояснення виробничих процесів, їх обслуговування та керування, покращення вивчення інших предметів (фізики, хімії, біологія, географія, креслення, трудового навчання тощо). Відомо, що ефективним є навчання, яке в поєднанні з вихованням забезпечує активізацію мислення учнів і свідоме засвоєння ними системи наукових знань, викликає у них бажання та потребу в цих знаннях і збільшує інтерес до предмета, допомагає розвитку здібностей кожного учня, розвиває вміння та навички застосовувати отримані знання в житті, а також самостійно здобувати ці знання. Підвищенню ефективності навчання математики сприяє розв'язування задач прикладноого та практичного змісту. Потрібно так організовувати вивчення математики, щоб воно було корисним і водночас захоплюючим, цікавим. 

Прикладні задачі на уроці виконують кілька функцій. Задачі показують зв'язок математики з життям, їх розв’язання покращує економічну грамотність учнів, задача виховує інтерес до математики. Задачі практичного змісту переконують учнів у потребі вивчення теоретичного матеріалу і показують, що математичні абстракції виникають із задач, поставлених реальним життям. Учні набувають досвід роботи з довідниками, навчаються самостійно знаходити потрібну інформацію в додатковій літературі. Даний вид діяльності дозволяє формувати такі компетентності:

•       пізнавальну: її використання спрямоване на формування у школярів системи знань, умінь та навичок на різних етапах навчання;

•       інформаційну: розвиває вміння працювати з різними джерелами інформації, осмислювати зміст понять, застосовувати здобуті знання на практиці, аналізувати результати, розширювати кругозір, робити відповідні узагальнення, порівняння, висновки;

•       соціальну: міжпредметні зв’язки на уроках математики можуть здійснюватися насамперед через ці задачі.

 Дотогож,  практичні задачі допомагають висвітити міжпредметні зв’язки, які в свою чергу обумовлюють поглиблене і розширене сприйняття учнями фактів, свідоме засвоєння теорії, формування цілісної картини природи. 

 Такі задачі забезпечують посилення мотивації навчання математики, спонукають учнів до здобуття нових знань, оволодіння новими вміннями, збагачують їх знаннями з інших предметів.

 Одним iз засобів вирішення цих завдань є продумане використання на уроках математики задач практичного змісту, до розв'язання яких, як показує досвід роботи, учні мають більший потяг, ніж до бiльшостi задач iз шкільних пiдручникiв. В Г. Болтянський писав ,що «задачi прикладного характеру мають у загальноосвiтнiй школі важливе значення перш за все для виховання в учнів iнтepecy до математики. На прикладі  добре складених задач прикладного змісту учні будуть переконуватись у значенні математики для різноманітних сфер людської діяльності, в її користі i необхідності для практичної роботи, побачать широту можливих застосувань математики, зрозуміють її роль в сучасній культурі».

 Отже, розв'язуючи прикладні задачі, учні не тільки засвоюють математичні поняття, вивчають математичну символіку, уміють наводити докази, але й розуміють взаємозв'язок теорії з практикою, усвідомлюють необхідність вивчення математики, набувають навичок у розв'язаннi проблемних ситуацій, що виникають у повсякденному житті . У процесі розв'язання таких задач в учнів формуються пізнавальна, інформаційна та соціальна компетентності.

 

 

2.2 Методичні аспекти використання прикладних та практичних задач

при вивченні математики у 5-6 класах

 

Розв’язування прикладних задач у шкільному курсі математики сприяє ознайомленню учнів із роботою підприємств і галузей народного господарства, викликає інтерес до різних професій. Задача має демонструвати практичне застосування математичних ідей і методів та ілюструвати матеріал, що вивчається на певному уроці, містити відомі або інтуїтивно зрозумілі учням поняття й терміни, а також реальні числові дані.

При використанні задач з практичним змістом в 5-6 класах необхідно враховувати вікові особливості учнів: 

1. В учнів переважає в цей період образна пам'ять, але потім її значення зменшується. Тим не менш, результат запам'ятовування зазвичай вище при опорі на наочний матеріал. Це означає, що доцільність використання тих чи інших засобів наочності залежить від того, чи сприяє діяльність, безпосередньою метою якої є освоєння цієї наочності, іншої діяльності з оволодіння учнями знаннями, заради засвоєння яких і використовуються ці засоби наочності. Якщо ці дві діяльності не пов'язані між собою, то наочний матеріал марний, а іноді навіть може грати роль відволікаючого чинника. Розглянемо приклад, що ілюструє залежність уваги від використання наочного матеріалу: Швидкість велосипедиста на 4 км / год більше, ніж швидкість вершника. Через 4 год відстань між ними стала 42 км. Знайти швидкості велосипедиста і вершника, якщо початкова відстань між ними дорівнює 114 км. У цьому випадку краще використовувати схему 2.1, зображену нижче: 

 

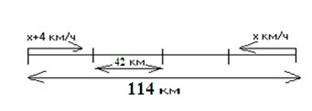
Схема 2.1 - Схематичне зображення задачі 

 

2.      У цей період розвиваються обчислювальні та інтелектуальнопізнавальні здібності учнів, збільшується прагнення до самостійної діяльності, виробляється воля досягнення мети в навчанні, діяльність стає осмисленою. Тому, щоб в учнів було прагнення до навчання, потрібно йти трохи попереду їх розвитку, але при цьому спиратися на принцип доступності, тобто йти в межах зони найближчого розвитку. Навчання повинно бути особистісно-орієнтованим. 

3.      Учням важко зосередитися на одноманітній і малопривабливій для них діяльності або на діяльності цікавій, але потребуючій розумового навантаження. Щоб утримувати свою увагу на інтелектуальних задачах, діти повинні докласти зусиль, тому на уроці потрібно часта зміна видів діяльності. 

4.      Мимовільне запам'ятовування є більш продуктивним, ніж довільне.

Це стає можливим, якщо учень розуміє те, що він повинен запам'ятати. 

Так, у 5-му класі, вивчаючи дії над натуральними (особливо багатоцифровими) числами, дітям пропонується: обчислити, скільки води, їжі потребує середньостатистична людина за своє життя, і перерахувати отримані результати на кількість товарних вагонів залізничного потяга; з'ясувати, чи може людина прожити мільйон хвилин або мільярд секунд; полічити, за скільки часу сонячне світло досягає Землі.

 У 5-6  класах використовуються дидактичні ігри з розподіленням ролей, які відповідають різним професіям, завдання, з вирішенням певних виробничих чи побутових проблем є дієвими. Застосування прикладних задач дає можливість вдало створювати проблемні ситуації на уроці (Скільки потріно ламінату, щоб зробити підлогу прямокутної форми з певними розмірами).

У 5 класі протягом І семестру учні в основному вивчають натуральні числа і дії над ними, роблячи ухил на розв’язування рівнянь і, особливо, текстових задач. Саме на текстові задачі слід звернути особливу увагу, оскільки  в більшості вони є прикладними, наприклад, задачі економічного змісту чи задачі на рух. Оскільки в учнів переважає в цей період образна пам'ять, то процес розв’язування задачі слід розпочати з наочного зображення. На цьому етапі дуже важливо не перебільшитити, а саме: не слід супроводжувати схему докладними малюнками, вимальовуючи на дошці потяги, автомобілі, корзини з яблуками, мішки тощо, оскільки діти почнуть переносити малюнок в зошит, що займе багато часу і урок математики ризикує перетворитись в урок малювання. Отже, схема має бути якомога більш абстрактною і зображатись, по можливості, від руки, там не має бути елементів, складніших за прямокутник. Слід за цим необхідно перейти до аналізу задачі, але перед цим необхідно пригадати основні співвідношення між величинами (якщо це задача на рух, то це відстань-час-швидкість, якщо це задача економічного змісту, то це кількість-ціна-вартість). Після цього необхідно визначити, що нам відомо, що потрібно знайти, що для цього необхідно знати і т.

д. На цьому етапі перевага надається фронтальним методам роботи, даючи можливість висловитись усім бажаючим, що сприяє розвитку логічного мислення та навичок математичної мови. 

У курсі математики 5 класу особливе місце посідає досить велика кількість геометричного матеріалу. Саме тут виникає найбільше можливостей щодо реалізації практичного підходу до навчання математики. Особливу увагу слід приділяти саме практичним задачам, де необхідно не лише обчислити, а й виміряти. Можна вирізати з паперу певні фігури, які складаються з прямокутників і запропонувати учням визначити їх площу. 

 По закінченню вивчення цієї теми можна цілий урок присвятити розв’язуванню практичних задач, наприклад: 

1)     Визначити скільки фарби необхідно для фарбування підлоги в цьому класі.

2)     На кожного учня класу повинно припадати не менше, ніж 6 м^𝟑 повітря.

На скільки учнів розрахована класна кімната, розміри якої 10 м, 8 м, 3 м?

3)     Екскаватор викопав яму, яка має форму куба, ребро цього куба дорівнює 4 м. Скільки потрібно вантажівок, щоб вивезти всю глину, якщо вантажність однієї машини 3 т, 1 м^𝟑   глини має масу 1600 кг.   

Особливу увагу прикладним задачам слід приділити під час вивчення відсотків. Уся ця тема є прикладною. Тут необхідно приділити увагу задачам економічного змісту.

У 6 класі першою темою є «Подільність натуральних чисел». Учні добре сприймають цю тему, але мала кількість прикладних задач у підручнику призводить до того, що втрачається мотивація навчання, а в кінцевому результаті знижуються якісний показник успішності. Саме тому тут вчителю необхідно самому розробити певну кількість завдань практичного змісту самостійно, з розрахунку щоб мінімум одна така задача була присутня на кожному уроці. 

При вивченні теми «Звичайні дроби та дії з ними» можна використовувати такі  прикладні задачі:

1)      Тривалість життя берези 150 років. Сосна живе у 2   рази довше берези.

Мамонтове дерево живе у 5 разів довше за сосну. Яка тривалість життя мамонтового дерева?  

2)      Із найважливіших культурних рослин земної кулі  походить з Азії,  походить з Америки,  з Африки. з інших частин світу – 90 рослин. Скільки всього найважливіших культурних рослин на земній кулі?

Діти з цікавістю розв’язують такі задачі, розуміють зв'язок математики з географією та біологією та покращують свою успішність з даних предметів. Розв’язуючи задачі  економічного змісту, учні відображають зв'язок математики з повсякенним життям. Наприклад: 

1)     На ремонт стальної лампи  використано  шматка дроту, ще треба замінити проводку в кімнаті розміром 4х5 (заміну потрібно виконати по двох сусідніх стінах). Скільки потрібно дроту?

2)     Вінницьким автодором за три тижні було відремонтовано 108 км. дороги. За перший тиждень було відремонтовано   дорога, за другий  решти. Скільки кілометрв дороги відремонтували за третій тиждень?  

Великий простір для використання практичних і прикладних задач дає тема: «Відношення і пропорції». Саме тут дуже багато завдань сприяє розвитку міжпредметних зв’язків, особливо з такою наукою, як географія. Тому під час вивчення масштабу слід використовувати якомога більше наочності: географічні карти, атласи, глобус, плани будівель тощо. Стосовно довжини кола рекомендується використовувати задачі, в умовах яких згадуються предмети, близько знайомі учням, наприклад, колесо, обруч тощо. 

У ІІ семестрі учні працюють з раціональними числами, які традиційно вводяться через поняття температури (вище нуля, нижче нуля) та понять «нижче рівня моря», «вище рівня моря». Але надалі прикладні задачі майже не застосовуються. Тому бажано вчителю додатково розробити задачі економічного змісту. Під час вивчення координатної площини потрібно приділити час міжпредметним зв’язкам.  

Отже, розв’язування задач прикладного та практичного змісту при вивченні курсу математики 5 – 6 класу забезпечують посилення мотивації навчання математики, спонукають учнів до здобуття нових знань, оволодіння новими вміннями, збагачують їх знаннями з інших предметів, ознайомленню учнів із роботою підприємств і галузей народного господарства, викликають інтерес до різних професій, сприяють підвищенню рівня якості освіти.

      

РОЗДІЛ ІІІ. ЗАДАЧІ ПРИКЛАДНОГО ТА ПРАКТИЧНОГО ЗМІСТУ У

ВИВЧЕННІ МАТЕМАТИКИ 5 КЛАСУ

 

 

3.1. Площина. Пряма. Промінь. Відрізок

 

Навчальна  мета: сформувати уявлення про площину, поняття прямої, променя; сформувати вміння розрізняти і зображувати прямі, промені, відрізки; спрямувати практичні дії учнів на наочне усвідомлення властивостей прямої; формувати пізнавальну та соціальну компетентність.

 

Методичні рекомендації

 Перш ніж розглядати з учнями поняття «площина», «пряма», «промінь» потрібно познайомити їх з описами більш загальних геометричних об’єктів: поверхня, лінія, точка.

Запропоновані вправи сприяють формуванню вміння розпізнавати, зображати і позначати прямі та промені, а також розумінню того, що прямі та промені нескінченні, вони не мають довжини, а відрізок має довжину.

В підручнику дається означення, що рівними називаються відрізки, які суміщаються при накладанні. Для закріплення цього поняття можна запропонувати задачу:

Щоб зробити огорожу для городу квадратної форми, відрізали 4 шматки дроту. Як перевірити, що ці 4 шматки підійдуть?

Дійсно, якщо 4 шматки будуть рівними, то вони підійдуть і перевірити це можно накладанням цих відрізків один на одного.

                 Такі задачі можна використовувати на різних етапах уроку:

1)  мотивації навчальної діяльності;

2)  формування навичок і вмінь;

3)  систематизації та узагальнення навчального матеріалу.

 

Задачі

1.       Щоб зробити огорожу для городу квадратної форми, відрізали 4 шматки дроту. Як перевірити, що ці 4 шматки підійдуть? (Відповідь. Будуть рівними)[1]

2.       Як з'єднати всі точки (рис. 3.1), провівши лише 4 відрізки?  [12]

Рис. 3.1

 

3.      На мотузці зав’язали п’ять вузлів. На скільки частин ці вузли розділили мотузку? ( Відповідь: на 6 частин.) [19]

4.      Щоб розрізати дошку на 7 частин, тато зробив декілька відміток. Скільки відміток має зробити тато? ( Відповідь: 6 відміток.) [27]

5.      Шматок дроту довжиною 102 см потрібно розрізати на частини довжиною 15 см і 12 см без обрізків. Як це зробити ? Скільки  розв’язків має задача? (Відповідь. 6 і 1; 2 і 6 частини.)  [27]

6.      Телеграфні стовпи розміщені один від одного на відстані 60 м. Скільки стовпів потрібно встановити на відстані 9 км? ( Відповідь: 151 стовп.) 

 

 

3.2. Кут 

 

  Навчальна  мета: формувати в учнів розуміння понять кута, вершини, сторони кута, бісектриси кута, познайомити з позначенням кута, сформувати уміння будувати кути; ознайомити учнів з порівнянням кутів і їх видами залежно від величини кутів, навчити розпізнавати різні види кутів залежно від величини кутів і будувати кути за заданою величиною; формувати пізнавальну та соціальну компетентність.

Методичні рекомендації

 Запропоновані задачі сприяють розумінню видів кутів та чим вони відрізняються один від одного. Такі задачі допомагають розпізнавати прямі, гострі, тупі та розгорнуті кути. Визначати вид кута за його рисунком. Перед розв’язуванням задач потрібно сформувати основні поняття, а лише потім відшукати приклади у навколишньому світі, опираючись на попередній досвід учнів. При формуванні навичок розпізнавати гострі, прямі та тупі кути доцільно розглянути задачі:

1.      Який кут утворюють на циферблаті годинника хвилинна і годинна стрілки, коли годинник показує: а) 6 год; б) 11 год; в) 8 год; г) 15 год; д) 18 год; є) 9 год?

[18]

2.      Годинник показує дванадцяту годину. Котру годину показуватиме годинник, якщо хвилинна стрілка повернеться на 30°; 60°; 90°; 120°; 150°; 180°? [18]

3.      Годинник показує шосту годину. Котру годину показуватиме він, якщо хвилинна стрілка повернеться на 180°? На який кут повернеться при цьому годинна стрілка? [18]

                 Такі задачі можна використовувати на різних етапах уроку:

1)  мотивації навчальної діяльності;

2)  формування навичок і вмінь;

3)  систематизації та узагальнення навчального матеріалу.

Задачі

1.      Який кут утворюють на циферблаті годинника хвилинна і годинна стрілки, коли годинник показує: а) 6 год; б) 11 год; в) 8 год; г) 15 год; д) 18 год; є) 9 год? 

(Відповідь: а) 180⁰;  б) 30⁰;  в) 150⁰; г) 90⁰;  д) 180⁰; є) 90⁰.) [18]

2.      Годинник показує дванадцяту годину. Котру годину показуватиме годинник, якщо хвилинна стрілка повернеться на 30°; 60°; 90°; 120°; 150°; 180°? (Відповідь:

13 год;  14 год;  15 год; 16 год;  17 год; 18 год.)  [18]

3.       Годинник показує шосту годину. Котру годину показуватиме він, якщо хвилинна стрілка повернеться на 180°? На який кут повернеться при цьому годинна стрілка? (Відповідь: 18 год 30 хв; 15⁰.) [18]

4.       У п’ятикутнику відрізали один кут. Яку одержали фігуру? (Відповідь:

шестикутник або чотирикутник.) [30]

5.       Шайби розміщені в точках С і D. Штанги воріт розміщені в точках А і В. Спочатку на око визнач, який з кутів АСВ чи АDВ більший, а потім перевір вимірювання кутів транспортиром. Запиши величину кутів АСВі АDВ (рис.3.2).

[19]

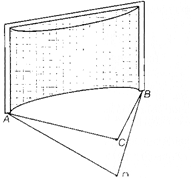
                                                           Рис. 3.2

 

 

3.3. Площа прямокутника і квадрата

 

 Навчальна  мета: ввести поняття одиниці площі, сформувати вміння учнів знаходити площу прямокутника та квадрата, формувати навички роботи з різними одиницями площі; формувати пізнавальну та соціальну компетентність.

 

Методичні рекомендації

Такі задачі допоможуть удосконалити знання учнів про площі прямокутника і квадрата, навчать застосовувати знання про  площу та її властивості під час розв’язування задач на комбінації геометричних фігур. На уроці вдосконалення вмінь та навичок бажано навчити учнів розв’язувати задачі:

а) на обчислення сторони прямокутника за площею та відомою стороною;

б) дослідження залежностей між S, а і в;

в) на застосування формул площ прямокутника та квадрата;

г) обчислення площ фігур, що є комбінальцією декількох прямокутників:

 Виконай потрібні вимірювання і обчисли площу зафарбованої частини многокутника (рис. 3.3). 

 

                                                                  Рис. 3.3

 

Такі задачі можна застосовувати на різних етапах уроку:

1)    мотивація навчальної діяльності;

2)    формування навичок і вмінь;

3)    систематизація та узагальнення навчального матеріалу;

4)    повторення навчального матеріалу; 5) домашнє завдання.

Задачі

1.                 Виконай потрібні вимірювання і обчисли площу зафарбованої частини

многокутника (рис. 3.4). [11] 

                                                                  Рис. 3.4

      

2.                 Щоб огородити ділянку квадратної форми, потрібно вздовж кожного боку встановити 9 стовпців. Скільки всього стовпців потрібно встановити вздовж периметра квадрата? (Відповідь: 32 стовпці.) [27]

3.                 На фарбування підлоги в спальні пішло 3 літри фарби, скільки потрібно фарби, щоб пофарбувати підлогу у їдальні, якщо її площа дорівнює 48м², а площа спальні 16м². (Відповідь: 9 л.)

4.                 Для фарбування 1 м² підлоги витрачається 120 г фарби, обчислити масу фарби, потрібної для фарбування вашої класної кімнати. У банці 2,8 кг фарби. Скільки банок фарби необхідно придбати для фарбування підлоги. 

5.                 Запиши формулу для обчислення периметра, зображеної на рис. 3.5 фігури.[11]

 

 

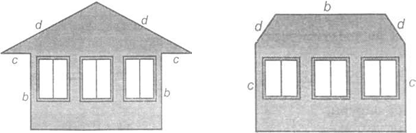
                                                                 Рис. 3.5

6.                 Скільки дошок потрібно, щоб застелити підлогу в кімнаті довжиною 15 і шириною 10 м, якщо довжина дошки 6м, а ширина 0,25м? (Відповідь: 100 дошок)

 

 

3.4. Об’єм прямокутного паралелепіпеда і куба

 

Навчальна  мета: сформувати поняття об’єму тіла; ознайомити з одиницями вимірювання об’єму; формувати вміння обчислювати об’єм прямокутного паралелепіпеда і куба; формувати пізнавальну та соціальну компетентність.

 

Методичні рекомендації

Учні вперше знайомляться з новою геометричною фігурою – прямокутним паралепіпедом. Потрібно наводити багато прикладів, що допоможуть уявленню про прямокутний паралепіпед. Рекомендовані задачі сприяють розвитку просторової уяви, формуванню пізнавальної та соціальної компетентностей. 

На уроці систематизації знань, умінь та навичок можна запропонувати такі задачі:

Виміряй довжину, висоту і ширину класної кімнати. Знайди об’єм кімнати. Обчисли, який об’єм повітря класної кімнати припадає на одного учня.

Результати вимірювань і обчислень запиши в таблицю 3.1:

 

Таблиця 3.1

Довжина, м	Ширина, м	Висота, м	Об’єм, м3	Кількість учнів	Об’єм, що припадає на одного учня, м3

 

Учням цікаво розв’язувати задачі пов’язані з навколишнім світом. Якість знань від цього тількі покращується.

Такі задачі учитель може на свій розсуд використовувати на різних етапах уроку, серед яких є:

1)  мотивація навчальної діяльності;

2)  формування навичок і вмінь;

3)  систематизація та узагальнення навчального матеріалу;

4)  повторення навчального матеріалу; 5) домашнє завдання.

Задачі

1.                 Яка із заданих фігур не може бути розгорткою куба? (рис. 3.6) [31]

 

                                                              Рис. 3.6

 

2.                 Із восьми рівних кубиків складають прямокутні паралелепіпеди. Зобрази всі можливі варіанти. Порівняй об’єми цих паралелепіпедів. (рис. 3.7) [1]

 

Рис. 3.7

 

Які розміри паперу, з якого зробили розгортку паралелепіпеда? (рис. 3.8)

(Відповідь: 50 см х 80 см.)  [31]           

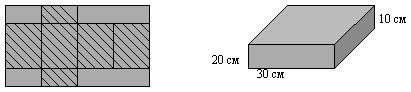
Рис. 3.8

 

4. Обчисліть об’єм фігури, зображеної на рис. 3.9. (Відповідь: 1) 336 куб. од; 2)

138 000куб. од; 3) 13 000 куб. од.) [19]

                                                           

 

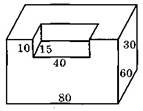
Рис. 3.9

5. За даною розгорткою склей прямокутний паралелепіпед та знайди його об’єм. (рис. 3.10) (Відповідь: 6000 см³.) [31]

 

 

Рис. 3.10

6.   Виміряй довжину, висоту і ширину класної кімнати. Знайди об’єм кімнати. Обчисли, який об’єм повітря класної кімнати припадає на одного учня.

Результати вимірювань і обчислень запиши в таблицю 3.2:

Таблиця 3.2

Довжина, м	Ширина, м	Висота, м	Об’єм, м3	Кількість учнів	Об’єм, що припадає на одного учня, м3

 

7.   Заповни таблицю 3.3:

Таблиця 3.3

Приміщення	Довжина, м	Ширина, м	Висота, м	Площа, м2	Об’єм, м3
Кухня
І-ша спальня
ІІ-га спальна
Вітальня
Коридор
Туалет
Ванна кімната
Вся квартира

 

На одного члена сім’ї припадає____м²  .

        На одного члена сім’ї припадає ____ м³ повітря.                                        

РОЗДІЛ ІV.  ЗАДАЧІ ПРИКЛАДНОГО ТА ПРАКТИЧНОГО ЗМІСТУ

У ВИВЧЕННІ МАТЕМАТИКИ 6 КЛАСУ

 

 

4.1. Масштаб

 

Навчальна  мета:  сформувати поняття масштабу; формувати вміння й навички розв’язувати вправи на знаходження відстані на карті;  формувати пізнавальну та соціальну компетентність учнів.

 

Методичні рекомендації

Учні мають розуміти поняття «масштаб» та навчитися знаходити відстань на місцевості за допомогою карти. Зображення у зменшеному вигляді має властивості: відстань між будь якими точками на місцевості зменшена в одну й ту саму кількість кількість разів. 

Запропоновані заачі допоможуть сформувати поняття масштабу; формувати вміння й навички розв’язувати вправи на знаходження відстані на карті, формувати пізнавальну та соціальну компетентність.

Для підведення підсумків уроку учням можна запропонувати такі задачі:

1.      Відстань між будинком і колодязем на місцевості становить 80 м, на плані – 4 см. У якому масштабі складено план? 

2.      Визначте площу земельної ділянки, що підлягає приватизації, якщо на плані масштабу 1 : 5000 вона має форму квадрату з стороною 20 мм.

3.      Відстань між берегами річки на плані масштабу 1: 2000 дорівнює 5 см. Яку відстань необхідно подолати на місцевості, щоб перепливти річку.

А домашнім завданням може бути така задача:

 Накресли план своєї квартири в масштабі 1:100.

 Такі задачі учитель може на свій розсуд використовувати на різних етапах уроку, серед яких є:

1)  мотивація навчальної діяльності;

2)  формування навичок і вмінь;

3)  систематизація та узагальнення навчального матеріалу;

4)  повторення навчального матеріалу; 5) домашнє завдання.

Задачі

1.   Переведіть числовий масштаб в іменований: 1: 2500; 1: 10 0000, 1: 400 0000, 1: 1000, 1: 400 00, 1: 1 000 000, 1: 250 0000, 1:2 000 00, 1:300 00, 1: 20 000, 1: 1 0000.

(Відповідь: 1) в 1 см 25 м; 2) в 1 см 1 км; 3) в 1 см 40 км; 4) в 1 см 10 м; 5) в 1 см 400 м; 6) в 1 см 10 км; 7) в 1 см 25 км; 8) в 1 см 2 км; 9) в 1 см 300 м; 10) в 1 см 200 м; 11) в 1 см 100 м.)

 

2.   Відстань між будинком і колодязем на місцевості становить 80 м, на плані – 2 см. У якому масштабі складено план? (Відповідь: 1:4 000.)

 

3.   Визначте площу земельної ділянки, що підлягає приватизації, якщо на плані масштабу 1 : 5000 вона має форму квадрату з стороною 2 см.

(Відповідь: 1 га.)

 

4.   Відстань між берегами річки на плані масштабу 1: 1000 дорівнює 10 см. Яку відстань необхідно подолати на місцевості, щоб перепливти річку? ( Відповідь:

100м.)

 

5.   Відстань між джерелом і лісом на плані масштабу 1 : 10000 становить 5 см. На другому плані ця відстань становить 7,5 см. Який масштаб другого плану?

(Відповідь: 1:6667.)

 

6.   Накресліть план шкільного подвір’я.

План дій:

1)    Обстежте шкільне  подвір’я і визначте, форму якої фігури воно має.

2)    Виберіть масштаб для креслення, наприклад, 1:200.

3)    Виміряйте лінійні розміри подвір’я (якщо подвір’я має форму прямокутника, то виміряйте довжину і ширину подвір’я)

4)    Накресліть прямокутник з відповідними вимірами, враховуючи вибраний масштаб.

5)    Виміряйте відстані від будівлі школи до огорожі.

6)    Виміряйте розміри будівлі школи.

7)    Зобразіть будівлю школи на плані. Якщо будівля має форму прямокутника, достатньо накреслити прямокутник з відповідними розмірами, враховуючи масштаб та відстані до огорожі.

7. Накресли план своєї квартири в масштабі 1:200.

 

 

4.2. Довжина кола. Площа круга

 

Навчальна  мета:  сформувати уявлення про коло та його елементи; домогтися засвоєння залежності між радіусом і діаметром кола, формули для обчислення довжини кола; сформувати вміння зображати коло за допомогою циркуля, розв'язувати задачі,  які передбачають використання поняття кола та його елементів, застосування формули для обчислення довжини кола; сформувати уявлення учнів про круг, поняття площі круга; домогтися засвоєння формули для обчислення площі круга; сформувати вміння розв'язувати задачі, які передбачають використання поняття круга, застосування формули для обчислення площі круга; формувати пізнавальну та соціальну компетентність учнів.

 

Методичні рекомендації

Прикладні задачі цієї теми передбачають використання поняття кола та його елементів, застосування формули для обчислення довжини кола; формують уявлення учнів про круг, поняття площі круга, допомагають засвоєнню формули для обчислення площі круга, формуванню вміння розв'язувати задачі, які передбачають використання поняття круга, застосування формули для обчислення площі круга, формують пізнавальну та соціальну компетентність.

При повторенні навчального матеріалу можна  з учнями розв’язати таку задачу:

Клумба має форму круга. Довжина кола, що обмежує клумбу, дорівнює 31,4 м. На клумбі висаджують кущі троянд, відводячи під кожний кущ 0,8 м² землі.

Яку найбільшу кількість кущів троянд можна висадити на клумбі?

Ця задача допоможе повторити використання поняття кола та його елементів, застосування формули для обчислення довжини кола, уявлення учнів про круг, поняття площі круга, допомагаже засвоєнню формули для обчислення площі круга.

Такі задачі учитель може на свій розсуд використовувати на різних етапах уроку, серед яких є:

1)  мотивація навчальної діяльності;

2)  формування навичок і вмінь;

3)  систематизація та узагальнення навчального матеріалу;

4)  повторення навчального матеріалу; 5) домашнє завдання.

Задачі

1.      Клумба має форму круга. Довжина кола, що обмежує клумбу, дорівнює 31,4 м. На клумбі висаджують кущі троянд, відводячи під кожний кущ 0,8 м² землі. Яку найбільшу кількість кущів троянд можна висадити на клумбі? (Відповідь: 98 троянд.) [2]

2.      Яку найбільшу площу може випасти корова, яка прив’язана до кілка мотузкою завдовжки 2 метри? Відповідь: (25,12 м².)

3.      Щоб витягти відро води, треба корбу коловорота криниці повернути 30 разів. Знайдіть глибину криниці, якщо діаметр барабана 26 см. (Відповідь: 24,492 м.)

4.      Діагональ квадрата дорівнює 20 дм. Квадрат потрібно покрити кругом найменшого радіуса. Чому дорівнює площа цього круга? (Відповідь: 314 дм².)

5.      Треба пофарбувати круг радіуса 3 км. Скільки потрібно для  цього фарби, якщо на кожний квадратний метр витрачається 120 кг фарби (результат округліть до десятків)? (Відповідь: 3390 кг.)

6.      Знайдіть площі заштрихованих фігур, зображених на рис. 4.1, якщо сторони квадратів дорівнюють по 10 дм.  Відповідь: 1) 78,5 дм² ; 2) 28,5 дм² ; 3) 57 дм² ; 4) 157 дм².

 

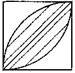                          1)           2)          3)         4)

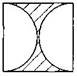
Рис. 4.1

7.  Уявіть собі, що земну кулю щільно обтягнули по екватору дротиною. Потім довжину дротини збільшили на 1 м, внаслідок чого між поверхнею земної кулі та дротиною утворилася щілина. Чи змогла б пролізти в цю щілину миша? 

Розв’язання:

                                                                                                               C                                                             C^1

Маємо                                         С        =        2πR, абоR         ;   С       + 1        =        2πR₁ або R₁ ^ ; 2 2

xR₁ RC^1  C  1  1  0,16 (м). Отже, щілина 2 2 2 6,28

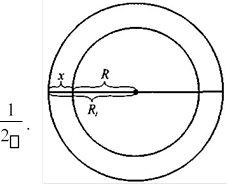матиме розмір близько 16 см. У таку щілину вільно може пролізти не тільки мишка, а й кішка! Величина щілини не залежить від радіуса кола. Це випливає з формули x Отже, коли замість земної кулі взяти, наприклад,

футбольний м'яч, то відповідь до задачі буде та ж. [32]

 

 

4.3. Кругові та стовпчасті діаграми

 

Навчальна  мета:  сформувати уявлення про подання інформації у вигляді кругових і стовпчастих діаграм; сформувати вміння розв'язувати задачі, які передбачають аналіз та побудову діаграм; формувати пізнавальну, інформаційну та соціальну компетентність учнів.

 

Методичні рекомендації

Прикладні задачі цієї теми допоможуть сформувати уявлення про подання інформації у вигляді кругових і стовпчастих діаграм, сформувати вміння розв'язувати задачі, які передбачають аналіз та побудову діаграм, формувати пізнавальну, інформаційну та соціальну компетентність учнів.

На початку уроку пропонується задача, наприклад:

Учні 6 класу за контрольну роботу з математики отримали оцінок високого рівня - 5, достатнього рівня - 12, середнього – 8. А тепер цю інформацію покажемо на рисунку 4.2. Яку інформацію сприймати краще? Звичайно з допомогою рисунка 4.2. Такі рисунки називаються круговими діаграмами.

 

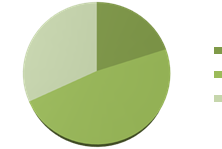
Рис. 4.2

Для засвоєння нових знань пропонуються задачі:

1.                 Побудуй кругову діаграму, яка зображує успішність учнів вашого класу з математики за 5 клас.

2.                 Побудуйте кругову діаграму бюджету вашої сім’ї.

За допомогою кругових діагром зручно зображати співвідношення між частинами одного цілого. Існує ще один вид діаграм, за допомогою яких зручно порівнювати за величиною декілько об’єктів. Такі діаграми називаються стовпчатими. Задачі:

1.   Побудуйте стовпчасту діаграму, яка зображає вагу членів вашої родини.

2.   Побудуйте стовпчасту діаграму для найбільших за чисельністю населення міст України, округливши числа до десятків тисяч: Київ — 2 640 тис.  жителів,  Харків — 1 464 тис., Дніпро — 1 062 тис., Одеса — 1 012 тис., Львів — 758 тис.

Учні повинні розуміти коли потрібно використовувати кругові діаграми, а коли яких стовчасті діаграми. Як домашнє завдання учням можна запропонувати скласти діаграми,  які відображають повсякденне життя. 

Такі задачі учитель може на свій розсуд використовувати на різних етапах уроку, серед яких є:

1)  систематизація та узагальнення навчального матеріалу;

2)  повторення навчального матеріалу; 3) домашнє завдання.

Задачі

1.                 Побудуйте стовпчасту та кругову діаграми розподілу площ приміщень трикімнатної квартири, якщо площа кухні становить 25% площі квартири, спальні — 20%, дитячої кімнати — 15%, вітальні — 30%, коридору — 10%.

2.                 Побудуйте стовпчасту діаграму для найбільших за чисельністю населення міст України, округливши числа до десятків тисяч: Київ — 2 640 тис.  жителів, Харків — 1 464 тис., Дніпро — 1 062 тис., Одеса — 1 012 тис., Львів — 758 тис.

3.                 Побудуйте кругову діаграму сімейного бюджету вашої сім’ї.

4.                 Побудуй кругову діаграму, яка зображує успішність учнів вашого класу з математики за I семестр.

5.                 Побудуйте стовпчасту діаграму, яка зображає вагу членів вашої родини.

6.                 Побудуйте стовпчасту діаграму, яка відображає зріст членів вашої родини.

 

 

4.4. Координатна площина

 

Навчальна  мета:  сформувати поняття координатної площини та її елементів; сформувати вміння знаходити координати точок; сформувати вміння будувати точки за їх координатами; сформувати поняття координатної чверті; сформувати вміння знаходити розташування точки на координатній площі залежно від знаків її координат; формувати пізнавальну, інформаційну та соціальну компетентність учнів. 

 

Методичні рекомендації

Прикладні задачі цієї теми формують поняття  координатної площини та її елементів; формують уміння знаходити координати точок та будувати точки за їх координатами, формують поняття координатної чверті, формують вміння знаходити розташування точки на координатній площі залежно від знаків її координат, формують пізнавальну, інформаційну та соціальну компетентність учнів. 

На початку уроку розглядається така інформація:

Метеорологи протягом доби кожні дві години вимірювали температуру повітря.

Результати вимірювань занесено в таблицю 4.1: 

Таблиця 4.1

Час, t (год)	0	2	4	6	8	10	12
Температура, °С	-1	0	1	2	3	5	7

 

Аналізуючи результати таблиці, можна зробити висновок, що температура повітря  пртягом доби змінювалась. Ці зміни можна побачити, побудувавши  графік залежності температури від часу. Сьогодні ви дізнаєтесь, що називається графіком, навчитесь будувати графіки залежностей між величинами.

Такі задачі учитель може на свій розсуд використовувати на різних етапах уроку, серед яких є:

1)  систематизація та узагальнення навчального матеріалу;

2)  повторення навчального матеріалу; 3) домашнє завдання.

Задачі

1.                 На аркуші паперу позначено 2 точки: А і В. Накресліть на цьому аркуші таку систему координат, щоб A(4;5) і B(-4;5).

2.                 Побудуйте графік руху човна, який рухається проти течії ріки, упродовж 5 годин після відплиття його від пристані, якщо власна швидкість 6 км/год, а швидкість течії 2,5 км/год.

3.                 Побудуйте на координатній площині ΔABC, якщо A(2; -1); B(7; -1);        

C(2;-5).

а) Знайдіть     координати          точок          перетину     сторін         трикутника      з        осями координат.

б) Через точку А проведіть пряму, паралельну стороні ВС, і пряму, перпендикулярну стороні ВС.

4.                 На рис. 4.3 зображено графік руху велосипедиста. За графіком визначте:

а) Яку відстань проїхав велосипедист за увесь час руху?

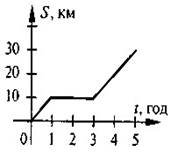б) Упродовж якого часу велосипедист відпочивав?                                                                

в)Яку відстань подолав велосипедист після зупинки?

                                                                                            Рис. 4.3

5.                 Побудуйте графік зміни температури повітря протягом 10 годин, використавши дані таблиці 4.2:

Таблиця 4.2

Час, t (год)	0	2	4	6	8	10
Температура, °С	-1	0	1	2	3	5

 

6.                 Накресліть на координатній площині замкнену ламану з веришнами в точках: 

(8; 9), (6; 8), (2; 8), (0; 9), (-4; 6), (-3; 2), (0; 0), (1; 2), (2; 1), (3; 1), (5; -1). (4; -2), (2; -

2), (2; -3), (5; -3), (6; -2), (6; 2). (7; 0), (10; 3), (10; 7); ламану з вершинами в точках:

(-4; 6), (-8; 6). (-11; 3). (-12; 0), (-14; -2), (-11; -1). (-10; -4). (-11; -8), (-8; -8), (-8; -7), (-7; -7). (-8; -3). (-8; -3). (-3; -9), (0; -9). (0; -4), (1; -4), (1; -5), (0; -7), (2; -9). (4; -5),

(4; -3). Позначте точки (2; 5) і (6; 5). Позначені точки А(2; 5) і В(6; 5) - очі «слона». [19] Відповідь:

 

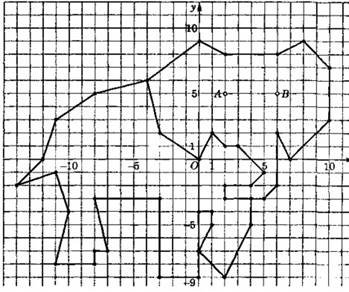
Рис. 4.4

7. Накресліть на координатній площині замкнену ламану, послідовними вершинами якої є точки з координатами: (-10; 6), (-9,5; 8), (-8; 10), (-7; 10), (-6; 9), (-6; 7), (-7; 3), (-7; 1), (-6; 2), (-4;3), (5;3), (3; 1), (7; 3), (7; 2), (6; 1), (7; 1), (5; -1), (7; -1), (10; 0), (8; -3), (4; -4), (0; -4), (-4; -3), (-9; -4), (-10; - 3), (-10; 0), (-7; 7), (-7; 8), (-

8; 7), (-9; 7). Позначте точку (-8,5; 8,5). Позначена точка А(-8,5; 8,5) – око «лебедя». [19] Відповідь:

 

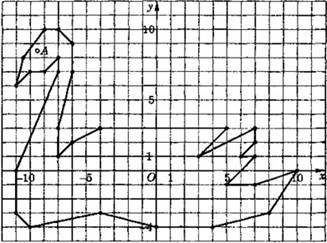
Рис. 4.5

6. На координатній площині позначте і сполучіть послідовно точки : 

а)   ;       ; ;       ; ; ; 

        б) ;       ; 

        в) ;       ;                                                                 ;

; 

        г) ;        ;         ; 

        д) ; ;         ;

        е) ;      ;         ;

        ж) ;       ;         ;

з) .

        и)    ;         .[17]

Відповідь:

 

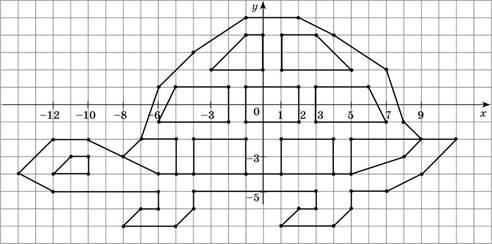
Рис. 4.6

      

ВИСНОВКИ

 

Реалізація  практичної та прикладної  спрямованності викладання  математики  сприяє  розв’язанню  одного  з  головних  завдань  сучасної  освіти  - її  індивідуалізації,   а  також  розвиває  дослідницькі  навички   учнів,  розширює  можливості  їх  соціалізації  через  оволодіння  ІКТ,   що  повинно  сприяти   планомірному  розвитку ключових  компетентностей,   які  дозволять  учню  сучасної  загальноосвітньої  школи  адаптуватися  в  постійно  змінюючих  життєвих  ситуаціях. 

Впровадження принципу практичного  спрямування  навчання  математики  впливає на зміну типу і структури  уроку, дає  благодатне  підґрунтя широкій інтеграції  з  іншими  предметами. Завдяки  прикладній  та  практичній  спрямованості  навчання учні розуміють, що математика  відображає  навколишній  світ,  числа,  дії, а  математична  термінологія  має  реальний  зміст.  Усе  це  запобігає  формальному  вивченню  предмета,  привчає  учнів  бачити  в  математиці  спосіб  дослідження  практичних завдань.

Застосування задач практичного змісту можна розглядати і як фактор мотивації навчальної діяльності учнів, бо що може краще мотивувати дитину, а ніж застосування отриманих знань, вмінь і навичок у процесі вирішення повсякденних життєвих проблем.

Шляхи  реалізації  прикладної  та  практичної  спрямованості  навчання  математики  є актуальними. Під час навчання  учень повинен  не  тільки  засвоїти  певні  знання, а й оволодіти способами  їх  застосування на  практиці, набути  широких  умінь  ефективного  використання математичних знань  у подальшій  діяльності у повсякденному житті.

Участь в PISA-2018 дозволить громадянам України, зокрема, спеціалістам у галузі освіти, об’єктивно оцінити стан середньої освіти в країні, усвідомити значущість поступових перетворень у цій сфері, політикам – приймати обґрунтовані рішення про необхідність змін.

Для реалізації прикладної спрямованості в навчанні математики велике значення має використання у викладанні різних форм організації навчального процесу. Розв'язуючи прикладні задачі, учні не тільки засвоюють математичні поняття, вивчають математичну символіку, але й розуміють взаємозв'язок теорії з практикою, усвідомлюють необхідність вивчення математики, набувають навичок у розв'язаннi проблемних ситуацій, що виникають у повсякденному житті. У процесі розв'язання таких задач в учнів формуються пізнавальна, інформаційна та соціальна компетентності.

Розв’язування задач прикладного та практичного змісту при вивченні курсу математики 5 – 6 класу забезпечують посилення мотивації навчання математики, спонукають учнів до здобуття нових знань, оволодіння новими вміннями, збагачують їх знаннями з інших предметів, ознайомленню учнів із роботою підприємств, викликають інтерес до різних професій, сприяють підвищенню рівня освіти в цілому.

Даний методичний посібник сприяє розвитку компетентної особистості, яка б здатна була до самоосвіти й саморозвитку, яка б уміла критично мислити, опрацьовувати різноманітну інформацію, змогла б використовувати набуті знання і вміння для творчого розв’язання проблем, яка б прагнула змінити на краще своє життя і життя своєї країни.

 

СПИСОК ВИКОРИСТАНА ДЖЕРЕЛ

 

1.           Бабенко С. П. Усі уроки математики (уроки 1-14). 5 клас (І семестр) / С. П.

Бабенко, І. С. Маркова. – Х.: Вид. група «Основа», 2013. – 301 с.

2.           Бабенко С. П. Усі уроки математики. 6 клас. І семестр (уроки 1 - 10)  / С. П.

Бабенко, І. С. Маркова. – Х.: Вид. група «Основа», 2014. — 284 с.

3.           Бевз Г. П. Методика викладання математики. Навч. пос. / Г. П. Бевз. – К.: Вища школа, 1989. – 367 с.

4.           Варданян С. С. Задачи по планиметрии с практическим содержанием: Книга для учащихся 6 – 8 классов средней школы / С. С. Вардянян. – М.: Просвещение, 1989.  143 с.

5.           Возняк Г., Маланюк М. Взаємозв'язок теорії з практикою в процесі вивчення математики/ Г. Возняк, М. Маланюк. - Рад. шк. -1989- 345 с.

6.           Гете И. В. Избранное. В 2-х ч., Ч. 2. / И. В. Гете. –М.: Просвещение. - 1985- с. 452.

7.           Державний стандарт базової і повної загальної середньої освіти [Електронний ресурс]. - Режим доступу: http://www.mon.gov.ua 

8.           Засуха В. А. Прикладна математика. Підручник / В. А. Засуха, В. П. Лисенко, Б.

Л. Голуб – К.: «Арістей», 2004. – 227 c.

9.           Збірник наукових статей студентів фізико-математичного факультету. // ФМФ. – 2014. – №8. – с. 364.

10.      Збірник цікавих задач [Електронний ресурс]. - Режим доступу до статті:

http://zadachki.in.ua/tochky/

11.      Істер О. І. Математика: підручник 5 клас, загальноосвітнього навчального закладу/ І. О. Істер - К.: Ґенеза, 2013.- 368 с.

12.      Істер О. С. Математика. 5 клас : книжка для вчителя (уроки 1-12)/ О. С.Істер,

О.І.Баришнікова, О.А.Карликова. К. : Генеза, 2013. - 184 с. : іл.

13.      Касіяненко Г. А., Мазуніна С. М., Кіслова Т. О., Жмурко І. Л. Задачі практичного змісту з геометрії 5-11 клас/ Автори – упорядники: Г. А. Касіяненко, С. М. Мазуніна, Т. О. Кіслова,  І. Л. Жмурко, Вінниця, 2013, 61 c.

14.      Колягин Ю.М., Пикан В.В. О прикладной и практической направленности обучения математике/ Ю. М. Колягин, В. В. Пикан // Математика в школе. - 1985. - №6. - с. 27-32.

15.      Кондратьєва Л.І. Збірник усних вправ з математики для 5 класу: підручник і посібник/ Кондратьєва Л.І. – Тернопіль, 2000.-64 с.

16.      Корнієнко Т.Л., Фіготіна В.І. Математика. 5 клас: плани-конспекти уроків на друкованій основі (уроки 1-11) / Т. Л. Корнієнко, В. І. Фіготіна - X. : Вид-во «Ранок», 2013. – 281 с.

17.      Корнієнко Т.Л., Фіготіна В.І. Математика. 6 клас : плани-конспекти уроків на друк. основі / Т. Л. Корнієнко, В. І. Фіготіна — Х. : Вид-во «Ранок», 2014. — 264 с. 

18.      Кут. Вимірювання і побудова кутів. Транспортир. Види кутів. Бісектриса кута

        [Електронний          ресурс].          -          Режим          доступу          до          статті:

http://edufuture.biz/index.php?title=%D0%9C%D0%B0%D1%82%D0%B5%D0%BC

%D0%B0%D1%82%D0%B8%D0%BA%D0%B0_5_%D0%BA%D0%BB%D0%B0% D1%81

19.      Мерзляк А. Г., Полонський В. Б., Якір М. С. Математика, 5 клас: книга для вчителя/ А. Г. Мерзляк - Х, Гімназія, 2005.- 144 с.

20.      Орос А.М Використання задач прикладного і практичного змісту  на уроках математики як засіб активізації пізнавальної діяльності учнів: Методичні рекомендації/ А. М. Опрос // Вище професійне училище №3. – м. Мукачево,

2009р. – 28 с.

21.      Офіційний сайт програми PISA-2018 в Україні [Електронний ресурс]. - Режим

        доступу                                                     до                                                     статті:

http://webcache.googleusercontent.com/search?q=cache:http://pisa.testportal.gov.ua/inf

o&gws_rd=cr&ei=lDBeWOSRHMiksAHSxKGYBQ

22.      PISA2018 – Україна [Електронний ресурс]. - Режим доступу до статті: 

http://testportal.gov.ua/pisa2018/

23.      Прикладні задачі в курсі математика  [Електронний ресурс]. - Режим доступу до статті: file://localhost/D:/Методичка%20практичні%20задачі%202016/referat20511/referat.html

24.      Прикладні задачі в курсі математика [Електронний ресурс]. - Режим доступу до статті: http://www.ukrreferat.com/index.php?referat=26565

25.      Рогожинська Е. К. Нові підходи до викладання математики в умовах реформування вітчизняної освіти: методичний лист / Укл. Е. К. Рогожинська. – Миколаїв: ОІППО, 2016 – 80 с.

26.      Старова О., Маркова С.  Математика: за підручником О.С. Істера, навчально – методичний посібник І семестр/ О. Старова  – Х.: Вид. група «Основа», 2013. – 128с.- серія «Мій конспект».

27.      Тарасенкова H. A. Математика 5 клас [Електронний ресурс]/ H. A., Тарасенкова, I.

М.Богатирьова, О. П. Бочко, О. М. Коломієць, 3. О. Сердюк. - Режим доступу до статті: http://ru.calameo.com/read/0029430443a4b2328def8

28.      Терешкин Н. Прикладная направленность школьного курса математики/ Н.

Терешкин // Просвещение. - 1990 - с. 153 - 212

29.      Точка. Площина [Електронний ресурс]. -Режим доступу до статті: http://svitppt.com.ua/geometriya/tochka-ploschina.html

30.      Урок захист проекту "Множення і ділення звичайних дробів" [Електронний ресурс]: Режим доступу до статті: http://www.teacherjournal.com.ua/multimedjnijurok/3758-zaxist-proektu-qmnozhennya--dlennya-zvichajnix-drobvq.html

31.      Урок. Практична робота [Електронний ресурс]. - Режим доступу до статті: http://festival.1september.ru/articles/314461/

32.      Уроки математики у 6 класі/ Ензельт Ольга. – Тернопіль: Підручники і посібники, 2007. – 320 с.

33.      Харланова Ю. В. Практические задачи в школьном курсе геометрии/ Ю. В.

Харланова//Математика в школе. – 2004. - №3. – с. 61 - 64.

 

      

ДОДАТОК

 

Тема: Об’єм прямокутного паралелепіпеда та куба Мета: 

•      навчальна: удосконалити вміння обчислювати об'єм прямокутного паралелепіпеда; домогтися засвоєння формули для обчислення об'єму куба; з формувати вміння виконувати вправи, що передбачають  обчислення об'єму куба.

•      розвиваюча: розвивати пізнавальну діяльність, мовний розвиток (називати приклади, пояснювати хід практичних дій), сенсоматорний розвиток (виконувати всі дії, необхідні в досягненні результату); розвивати зоровослухову пам'ять, увагу, логічне мислення (уміння лаконічно висловлювати свою математичну думку), розвивати уміння орієнтуватися в нестандартних ситуаціях, кмітливість, навички творчої роботи, комунікативні і соціальні компетенції; розвивати навички раціонального використовування часу.

•      виховна: виховувати  взаємоповагу, здорове суперництво, працьовитість, інтерес до математичних знань, виховувати уміння вислухати інших, виховувати активність, дисциплінованість, самокритичність, самостійність.

Тип уроку: удосконалення  знань і вмінь учнів.

Обладнання та наочність: презентація, таблиці, роздатковий матеріал. 

 

Хід роботи

 

І. Організаційний момент. 

                 Перевіряється готовність учнів до уоку.

ІІ. Мотивація навчального процесу.

 Сьогодні ми на уроці удосконалимо вміння обчисляти об’єм прямокутного паралелепіпеда та куба. Значення цієї теми дуже велике. Ці знання широко застосовуються у житті. Тому геометрію як науку, що виникла з  життя, повинен знати  кожен робітник, інженер, архітектор, художник, а також і ми з вами.

ІІІ. Перевірка домашньої роботи

Домашня практична робота

Виміряй довжину, ширину та висоту  кожної кімнати своєї квартири (будинку). Скільки квадратних метрів площі та скільки кубічних метрів повітря припадає на одного члена сім’ї.

Учні показують виконану практичну роботу.

ІV. Актуалізація знань.

Усні вправи та задачі

                        1.       Обчислити:

1) 3², 4², 5², 6², 7², 8², 9², 10²; 2)  2³, 3³, 4³, 5³.

2.                 Задача. 

Знайти об’єм фігури. Дивитись слайд №6

 

3.                 Задача.

Обчислити об’єм фігури. Дивитись слайд №7

 

4.                 Задача. 

Яка із фігур є розгорткою куба? Дивитись слайд №8

 

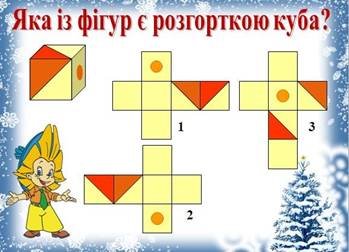
V. Удосконалення знань  План вивчення теми.

1.     Формула для обчислення об’єму куба.  Дивитись слайд №17,19 -21

2.     Приклад обчислення об’єму куба

Після повторення елементів прямокутного паралепіпеда та його властивостей учні знайомляться з елементами та властивостями куба. Знаходження об’єма куба демонструється в порівнянні з обємом прямокутного  паралепіпеда.

Об'єм прямокутного паралелепіпеда

𝑉 = 𝑎 ∙ 𝑏 ∙ 𝑐

Об'єм куба

𝑉 = 𝑎 ∙ 𝑎 ∙ 𝑎 = 𝑎³

 Одиниця вимірювання об'єму – куб із стороною V = 1 од³ (1 мм³, 1 см³, 1 дм³) Співвідношення між одиницями вимірювання величин

𝟏 дм^𝟑 = 𝟏𝟎𝟎𝟎 см^𝟑,

𝟏 м^𝟑 = 𝟏𝟎𝟎𝟎 дм^𝟑,

𝟏 м^𝟑 = 𝟏 𝟎𝟎𝟎 𝟎𝟎𝟎 см^𝟑,

𝟏 л = 𝟏 дм^𝟑,

𝟏 км^𝟑 = 𝟏 𝟎𝟎𝟎 𝟎𝟎𝟎 𝟎𝟎𝟎 м^𝟑.

 

VІ. Засвоєння нових знань і вмінь. Дивитись слайд № 23-27 Учням пропонується диференційований підбір задач.

 Початковий рівень Задача

                 Знайти об'єм куба якщо сторона дорівнює:

1)    2 см;

2)    4 см; 3) 5 см.

Середній рівень Задача

                  Маса 1 см³ міді 9 г. Яка маса куба, якщо довжина ребра 4 см? 

Достатній  рівень Задача

 На кожного учня класу повинно припадати не менше, ніж 6 м³ повітря. На скільки учнів розрахована класна кімната розміри якої 10 м, 8 м, 3 м?

Високий  рівень Задача

 Екскаватор викопав яму, яка має форму куба, ребро цього куба дорівнює         4 м. Скільки потрібно вантажівок, щоб вивезти всю глину, якщо вантажність однієї машини 3 т, 1 м³  глини має масу 1600 кг. 

VIІ. Самостійна робота

У заключній частині уроку перевіряється рівень засвоєння теми, учні виконують тестову самостійну роботу.

 

Варіант І                                                   Варіант ІІ

1.                 Знайти об'єм куба, ребро якого дорівнює

 

5 см		4 см
А) 125 см3	Б) 64 см3	В) 27 см3	Г) 16 см3

2.                 Обчисліть об'єм куба, якщо площа однієї з його граней дорівнює

 

9 см𝟐				25 см𝟐
А) 125 см𝟑		Б) 81 см𝟑	В) 27 см𝟑		Г) 9 см𝟑

 

3. Об'єм прямокутного паралелепіпеда дорівнює 140 м3, а два його виміри – 7м і 4 м. Чому дорівнює третій вимір цього паралелепіпеда?		3. Об'єм прямокутного паралелепіпеда дорівнює 168 м3, а два його виміри – 7м і 3 м. Чому дорівнює третій вимір цього паралелепіпеда?
А) 5	Б) 4	В) 8	Г) 9

 

4. Складське приміщення має форму прямокутного паралелепіпеда. Його площа дорівнює 312 м2, а об'єм - 1248 м3. Чому дорівнює висота цього приміщення?		4. Басейн має форму прямокутного паралелепіпеда. Його площа дорівнює 570 м2, а об'єм - 1710 м3. Чому дорівнює глибина цього басейну?
А) 3 м	Б) 4 м	В) 5 м	Г) визначити не можливо.

 

VIIІ. Захист проекту «Прямокутний паралелепіпед та куб у нашому житті»

IХ. Домашнє завдання

Параграф №26. Домашня різнорівнева  самостійна робота №5 с.199 – 200.

Підготуватися до контрольної роботи.

 

Х. Підсумок уроку

 Учитель підсумовує результати роботи з вивчення теми, звертає увагу на головні моменти й нагадує про те, що наступним уроком буде контрольна робота.

 

Презентація

[https://onedrive.live.com/view.aspx?cid=e58610ce249435cc&page=view&resid=E586 10CE249435CC!136&parId=E58610CE249435CC!177&app=PowerPoint]

     

Урок- експедиція

 

Тема:Множення і ділення звичайних дробів

 

Велику книжку природи можуть  читати лише ті, хто знає мову,  якою вона писалася. 

Цією мовою є математика.

                                           Галілей

 

 

               Мета уроку:

навчальна: узагальнити й систематизувати знання учні із теми «Множення і ділення дробів», уміння використовувати набуті знання при розв’язування нестандартних задач, швидко адаптуватися до нових умов, уміння використовувати час, підготувати учнів до написання контрольної роботи; розвиваюча: розвивати пізнавальну діяльність, мовний розвиток (називати приклади, пояснювати хід практичних дій), сенсоматорний розвиток (виконувати всі дії, необхідні в досягненні результату); розвивати зорово-слухову пам'ять, увагу, логічне мислення (уміння лаконічно висловлювати свою математичну думку), розвивати уміння орієнтуватися в нестандартних ситуаціях, кмітливість, навички творчої роботи, комунікативні і соціальні компетенції; розвивати навички раціонального використовування часу.

виховна: виховувати  взаємоповагу, здорове суперництво, працьовитість, інтерес до математичних знань, виховувати уміння вислухати інших, виховувати активність, дисциплінованість, самокритичність, самостійність.

Тип уроку: систематизація і  узагальнення знань, умінь учнів. Урокекспедиція.

Обладнання: комп'ютер, мультимедійний проектор, презентація, картки оцінювання та сигнальні картки. 

Очікувані результати: 

Після уроку учні зможуть використовувати засвоєні математичні поняття, терміни під час розв’язання  задач, знаходити проміжні етапи у розв’язанні задач різних видів, знаходити раціональні способи в їх розв’язанні, аналізувати вивчений матеріал.

Хід уроку.

 

І. Організаційний момент. 

Перевірка готовності учнів до уроку.

КАРТКА  ОЦІНЮВАННЯ

         

 

ПРИЗВИЩЕ, ІМ’Я____________________________________       КЛАС ________ 

 

№ завдання	1	2	3	4	5	6
Назва завдання
Кількість балів за завдання	1 зав. -1б.	по 1б.	12б.	6б. 9б. 12б.	9б.	12б.
Кількість набраних балів

 

ВСЬОГО БАЛІВ ___________                ОЦІНКА __________________

                                                

ІІ. Повідомлення теми і мети уроку.

Вступне слово вчителя:

Сьогодні на уроці ми здійснимо експедицію країною Математики. Як ви знаєте країна Математики дуже велика, тому ми сьогодні відвідаємо лише одну її область – Звичайні дроби.  Побуваємо на семи станціях, де перевіримо знання з теми «Множення і ділення звичайних дробів».

Щоб відправитися в експедицію, потрібно придбати квиток, а для цього Вам потрібно виконати таке завдання: заповнити пропущені місця в таблиці.

 

І варіант                         ІІ варіант

1.   Виконати множення:

                 

 

А	Б	В	Г

 

2.   Виконати ділення:

12 ÷                 8 ÷  

 

А	Б	В	Г
	4	16	36

 

3.   У книжці 120 сторінок Женя прочитав:

 книжки;                           книжки.

Скільки сторінок почитав Женя?

 

А	Б	В	Г
30 с.	40 с.	80 с.	90 с.

 

 

4.   Знайти значення виразу:

 

І варіант     ;             ІІ варіант       . 

 

А	Б	В	Г
1			1

 

Знайти значення виразу. Три учні розв'язують завдання на картці.

 

Завдання на картці:

Знайти значення виразу:   2  + (1  − 1 ) ÷ 1  ÷  

Відповіді: 9 .

Застосування знань, умінь та навичок 

Наша експедиція відправляється на станцію «Опорних знань».

ІІІ. Станція «Опорних знань»

1.   Як знайти добуток двох звичайних дробів?

2.   Як знайти дріб від числа?

3.   Які числа називають взаємно оберненими? Наведіть приклади.

4.   Як поділити один дріб на інший?

5.   Як знайти число за його дробом?

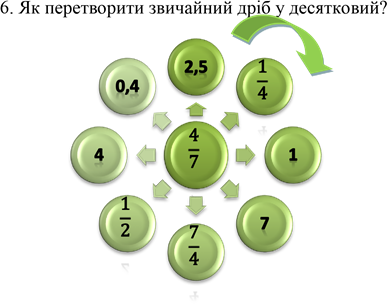
𝟏𝟔 𝟒 𝟒 𝟏𝟔 𝟖 𝟏 𝟏𝟎 𝟖 Відповіді: ,   , , ,   , , ,   .

                                     𝟕        𝟕     𝟒𝟗     𝟒𝟗      𝟕      𝟕       𝟕        𝟑𝟓

 

ІV. Станція «Історична»

Учні захищають проет, який готували з початку теми.

Проект «Звичайні дроби в давнину»

 

Мета проекту: вияснити, коли люди почали працювати з дробовими числами. 

Чи розв'язували у давнину задачі на дії з дробами?

 

Стародавня Русь

У стародавній Русі дроби називали частками, а згодом ламаними числами.

Окремі дроби мали спеціальні назви. Наприклад, - треть,  - півтреть,   - п’ятина,

 - десятина, тощо.

Запис дробів за допомогою риски став загальноприйнятим з ХVІ ст.

 

Стародавній Китай

У Давньому Китаї користувались десятковою системою числення. При записі чисел користувалися цифрами у формі ієрогліфів. Приблизно у ІІ ст. н.е. було складено трактат «Математика в дев’яти книгах». Ця книга була призначена для землемірів, техніків і рахівників і містила виклад правил дій над дробами.

 

Староданя Греція

У стародавній Греції звичайні дроби були відомі. Понад 2,5 тисячі років тому греки вміли виконувати арифметичні дії з звичайними дробами. Вони користувались і одиничними дробами, і дробами загального виду.

 

Стародавній Єгипет

В Єгипті з дробами оперували ще 4000 років тому. Про це свідчать стародавні документи, які збереглися з тих часів. Проте загального способу для позначення всіх дробів, як це прийнято тепер, коли чисельник записують зверху, знаменник знизу, а між ними ставлять риску, в єгиптян не було. При виконанні обчислень стародавні єгиптяни використовували лише так звані одиничні дроби – дроби з чисельником 1 і дріб  . Такі дроби єгиптяни зображали, ставлячи крапку над знаменником. Усі інші дроби вони зводили до одиничних. 

Задача з папірусу Ахмеса

 

 

Отже,  дробами оперували ще 4000 років тому.

 

V. Станція «Унція». А ви знаєте що таке унція? Дізнаєтесь після того, як розв’яжете рівняння. Перед вами рівняння різного рівня складності. Виберіть те, яке ви вважаєте за потрібне і самостійно розв’яжіть його.

 

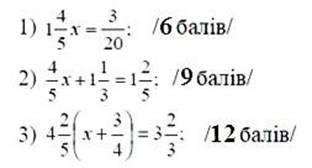
Розв'язком всіх рівнянь є дріб  Вибірково перевірити зошити кількох учнів.

Який корінь рівняння ви дістали? Отже, ви уже здогадались, що таке унція? Так називали дріб у стародавні римляни. Це дванадцята частина ваги. Ви  можете порахувати скільки складає унція від кілограма і що означає «з'їсти 3 унції сиру».

 

 

VІ. Станція «Флори та фауни »

Учням пропонується розв’язати задачі.

 

Задача 1

Тривалість життя берези 150 років. Сосна живе у  2    рази    довше берези.

Мамонтове дерево живе у 5 разів довше за сосну. Яка тривалість життя мамонтового дерева?  

 

                                                            Розв’язання 

 

7 1507

1)                            1502150   ₃               ₃                 ³⁵⁰ - стільки років живе сосна.

 

2)   350 · 5 = 1750 – стільки років живе мамонтове дерево.

 

Відповідь: 1750 років.

 

Задача 2

Із найважливіших культурних рослин земної кулі  походить з Азії,  походить з Америки,  з Африки. з інших частин світу – 90 рослин.

Скільки  всього найважливіших культурних рослин земної кулі?

Відповідь: 640 рослин.

VІІ. Станція «Прикладна»

Учні захищають проет, який готували з початку теми.

 

Проект «Звичайні дроби в житті людини »

 

Тема дослідження: використання правил множення та ділення дробів у професійній діяльності

Гіпотеза  дослідження:  наша група припускає, що не обов'язково знати правила множення та ділення звичайних дробів для виконання професійних обов'язків.

Мета дослідження: розвивати математичне мислення;виробляти здатність виділяти головне та вміння користуватись  готовими  алгоритмами  для певних завдань.

 

Результати дослідження:

Ми провели опитування батьків, сусідів, знайомих. Опрацювали та проаналізували велику кількість прикладних задач. Обрали деякі для прикладу.

 

 

Водій

Я відправився в рейс із пункту А в пункт В, відстань між якими 369 км. О 13 год. 30 хв. я проїхав дев’яту частину шляху. З якою швидкістю мені потрібно їхати, щоб прибути на фірму до її закриття (закривається о 18 год)?

 

Електрик

 

На ремонт стальної лампи  я використав ¼ шматка дроту, ще треба замінити проводку в кімнаті розміром 4х5 (заміну потрібно виконати по двох сусідніх стінах). Скільки потрібно дроту? 

 

 

Майстер по ремонту доріг

Робітниками Вінницького автодору за три тижні було відремонтовано 108 км дороги. За перший тиждень було відремонтовано 4/9 дороги, за другий 11/15 решти. Скільки кілометрв дороги відремонтували за третій тиждень? 

 

Висновок: правила множення та ділення звичайних дробів обов'язково знати всім та вміти їх застосовувати.

 

VІІІ. Домашнє завдання

 

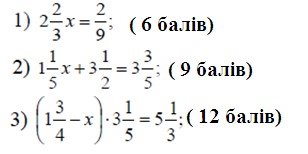
Задача 1

Водій 

Я відправився в рейс із пункту А в пункт В, відстань між якими 369 км. О 13 год 30 хв я проїхав дев’яту частину шляху. З якою швидкістю мені потрібно їхати, щоб прибути на фірму до її закриття (закривається о 18 год)? Задача 2

 Електрик

На ремонт стальної лампи  я використав  шматка дроту, ще треба замінити проводку в кімнаті розміром 4х5 (заміну потрібно виконати по двох сусідніх стінах). Скільки потрібно дроту? 

Підготуватись до КОНТРОЛЬНОЇ РОБОТИ

 

ІХ.  Підведення підсумків уроку. 

 

Рефлексія

1.     Як ви оцінюєте свою роботу на уроці?

2.     Які завдання виявилися складними? Чому?

3.     Яким питанням слід приділити більше уваги?

 

Заключне слово вчителя: Ось і закінчився урок. Молодці, ви добре

попрацювали.  «Велику книжку природи можуть читати лише ті, хто знає мову, якою вона писалася. Цією мовою є математика».

Отже, я Вам бажаю гарних успіхів у вивченні математики та пізнанні світу !!!       

Ділова гра «Сім мислячих капелюшків»

 

Щоб бути креативним, стати упередженим і критично мислячим, тим, хто вміє бачити позитивні і негативні сторони, не боїться відчувати, вчиться діяти і невідступно крокувати до наміченої мети - потрібно приміряти на себе капелюшки різного кольору.

Білий капелюх розмовляє мовою цифр і фактів, ходячий комп'ютер. Володар цього капелюшка  виконує роботу з першоджерелами зі збору інформації: за словниками, картами, таблицями, схемами.

«Чорний капелюшок - бродячий символ песимізму» - колір невпевненості, сприйняття життя в темному світлі.

Володар цього капелюшка  вказує на негативні сторони, безпеку, помилки.

Червоний капелюшок - це океан пристрастей та емоцій. Його девіз:

Доказів не треба.

Володар цього капелюшка формує своє ставлення до подій та їхніх учасників.

Жовтий капелюшок - джерело позитивних сподівань.

Господар цього капелюха простежує позитивні сторони явища, переваги та досягнення.

Зелений капелюх — творчо натхненний.

Він вказує на нові пропозиції, ідеї, альтернативи. 

Синій капелюшок - це контролер.

Цей капелюх контролює над розумовим процесом, висловленням коментарів та спостережень.

Фіолетовий капелюх — це координатор.

Володар цього капелюшка підводить підсумки.

До вашої уваги пропонується ділова гра «Сім мислячих капелюхів» на уроці математики.

Зараз ви учні. Спочатку клас об’єднується в 7 груп, бажано, щоб кількість учнів була однакова. Ми об’єднуємо вас за списком, а можна - за жеребкуванням, за бажанням учнів. Кожна група отримує завдання або запитання, на яке потрібно дати відповідь або підготувати невелике повідомлення . Заслуховування відповідей слід починати з білих капелюхів, тому що це робота з першоджерелами. Доповіді червоних, жовтих, чорних, зелених капелюхів можна використовувати в будь-якій послідовності, як вважає вчитель. Завершити роботу слід підведенням підсумків, а це зроблять сині  та фіолетові капелюшки.

Я пропоную фрагмент уроку з математики - тема «Одиниці вимірювання площі». Тривалість - 15-20 хвилин, проводиться на початку уроку як актуалізація опорних знань.

Тема: Одиниці вимірювання площі

Мета: розширити знання учнів про одиниці вимірювання площі. повторити призначення цих мір; ознайомити з давніми одиницями вимірювання площі; розвивати вміння логічно будувати свої відповіді, робити висновки, припущення, аналізувати і узагальнювати; виховувати комунікативність, пізнавальний інтерес до вивчення математики.

Попередньо вчитель дає завдання білим капелюхам підготувати повідомлення про одиниці вимірювання у різних країнах та у давнину. Діти працюють з додатковою літературою (енциклопедією, довідниками тощо).

Хід гри

Білі капелюшки  Завдання

üЯкі одиниці площі ви знаєте? Як вимірювали площі у давнину?

Чорні капелюшки Завдання

üВкажіть на недоліки виміру площ ?

Червоні капелюшки Завдання

üЯк ви думаєте, чому виникла необхідність появи одиниці площі.

Жовті капелюшки

Завдання

üЯкі переваги вимірювання площ сучасності над тим, як вимірювалися площі у давнину?

Зелені капелюшки Завдання

üЯк перевести різні одиниці виміру площі в СІ ?

Сині капелюшки Завдання

üЧому необхідно знати та вміти використовувати міри площ?

Фіолетові капелюшки Завдання

üЗробіть висновки з даної теми.

Наведена технологія дозволяє розглянути певну тему з  різних точок зору, виявити переваги та недоліки, висунути альтернативну точку зору, сприяє розвитку мислення та вмінню  вести дискусію, спонукає дітей до пошуку додаткової інформації, поширює світогляд; має форму групової діяльності, яка сприяє теплому неофіційному клімату. Мовчазні діти стають активними учасниками навчального процесу, хоча не брали участі  в роботі цілого класу. Цінним є те, що кожен учень має можливість вибрати різні ролі: експертів, що аналізують проблему; учасників, які шукають альтернативне розв'язання проблеми; мислителів, що аналізують взаємозв'язки між явищами; співрозмовників, котрі вміють активно слухати, домовлятися; партнерів, що вчаться співпрацювати тощо. 

Наведену технологію можна застосувати і як підсумок уроку. Кількість капелюшків за кольором обирає вчитель.

Дякую. Бажаю вам успіхів!

 

Презентація

[https://onedrive.live.com/view.aspx?cid=e58610ce249435cc&page=view&resid=E586 10CE249435CC!184&parId=E58610CE249435CC!182&app=PowerPoint]