Методична розробка "Довідничок - помічничок"

Про матеріал

Методична розробка "Довідничок - помічничок" для учнів та вчителів математики. Містить опорні конспекти для учнів та компетентнісні задачі.

Перегляд файлу

Предмети та одиниці лічби

Цифри: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Натуральні числа: 1, 2, 3, …, 37, …

Натуральні числа – числа, що вживають при лічбі предметів.

Властивості:

натуральних чисел безліч;
найменше натуральне число 1;
число 0 не є натуральним;
найбільшого натурального числа немає;
кожне наступне число більше від попереднього на 1.

Розряди: сотні, десятки, одиниці

Класи: одиниць, тисяч, мільйонів, мільярдів

Цифри – знаки для запису натуральних чисел.

Нумерація - спосіб читання або записування чисел.

Індуси – араби

- І 10 - X
- ІІ 50 - L
- ІІІ 100 - C
- IV 500 - D
- V 1000 - M

1 000 000 000 000 - трильйон

1 000 000 000 000 000 - квадрильйон

Шахи – винагорода – 18 446 744 073 709 551 615

18 квінтильйонів 446 квадрильйонів 744 трильйонів 73 мільярди 709 мільйонів 551 тисяча 615

Числові вирази. Рівності. Нерівності. Порівняння натуральних чисел

Числовий вираз: числа, дії – +, -, ·, :, дужки.

Числова рівність – це запис, у якому два числа, або два числових вирази, або числовий вираз і число сполучено знаком рівності.

Порівняти два числа – це означає з’ясувати, яке з них більше, яке – менше, або показати, що вони рівні.

Числова нерівність – це запис, у якому два числа, або два числових вирази, або числовий вираз і число сполучено знаком нерівності.

Знаки нерівності:

> - більше; ≥ - більше або дорівнює

< - менше; ≤ - менше або дорівнює

Кожне натуральне число > 0.

Приклади нерівностей:

7 > 3; 12 + 3 < 8 · 3; 2 + х > 5.

Більше число має більше цифр.
Більше число має більше одиниць у вищому розряді.

Подвійна нерівність: 3 < 5 < 7.

Читають: Число 5 більше 3 і менше 8.

Додавання натуральних чисел

Доданок + доданок = сума

Закони додавання:

переставний: від перестановки доданків сума не змінюється.

сполучний: від групування доданків сума не змінюється.

Додати до числа а число b означає збільшити число а на b одиниць.

Додавання буквених виразів

а + а + а + а = 4 · а = 4а

3с + 5d + c + 2d= 4c + 7d

Додавати можна лише такі буквені вирази, які містять ті самі букви.

Віднімання натуральних чисел

Зменшуване – від’ємник = різниця

Відняти від одного числа означає знайти таке третє число, яке в сумі з другим числом дає перше.

а – b = с  с + b = а

Віднімають від числа а число b тоді, коли хочуть:

за відомою сумою і одним із доданків знайти інший доданок;
зменшити число а на b одиниць;
дізнатися, на скільки одиниць число а більше за число b.

Щоб знайти невідомий доданок, треба від суми відняти відомий доданок.

Віднімання буквених виразів

5а – 2а =3а

3с + 5d – c – 2d = (3с – c) + (5d – 2d) = 2c + 3d

Віднімати можна лише такі буквені вирази, які містять ті самі букви.

Множення натуральних чисел

множник · множник = добуток

Помножити число а на натуральне число b – це означає взяти число а доданком b разів.

5 · 3 = 5 + 5 + 5

Властивості:

Яким би не було число а, завжди

Закони множення

переставний: від перестановки множників їх добуток не змінюється.

сполучний: від порядку групування множників добуток не змінюється.

Щоб помножити на число, записане одиницею з наступними нулями, достатньо до першого множника справа приписати стільки нулів, скільки їх є у другому множнику.

12 · 10 = 120; 123 · 100 = 12 300.

Правило:

Від збільшення одного множника в кілька разів добуток збільшується в стільки ж разів.

Властивості множення

Розподільний закон множення відносно додавання:

Добуток суми і числа дорівнює сумі добутків кожного доданка і цього числа.

Розподільний закон множення відносно віднімання:

Розкриття дужок – перетворення добутку в суму або в різницю.

2 · (4 + а) = 2 · 4 + 2 · а = 8 + 2а

Винесення множника за дужки – обернена дія до розкриття дужок.

3х – 3у = 3 (х – у)

Множення багатоцифрового числа на одноцифрове:

124 · 5 = (100 + 20 + 4) · 5 =

= 100 · 5 + 20 · 5 + 4 · 5 = 500 + 100 + 20 = 620

Степінь числа

Степінь – це добуток однакових множників.

(чотири в п’ятому степені)

5 множників

- степінь

4 – основа степеня, вона показує, яке число множили само на себе;

5 – показник степеня, він показує скільки рівних множників було в добутку.

Дію, за допомогою якої добуток рівних множників згортають у степінь, називають піднесенням до степеня.

Піднести число а до степеня п означає знайти добуток п множників, кожен з яких дорівнює а.

п множників

Правило. У виразах, що містять степені, спочатку виконують піднесення до степеня, а потім множення і ділення, додавання і віднімання.

Другий степінь називають квадратом числа а.

а² читається а в квадраті

а² = а · а; 3² = 3 · 3 = 9.

Третій степінь називають кубом числа а.

а³ читається а в кубі

а³ = а · а · а; 2³ = 2 · 2 · 2 = 8.

§ 13. Ділення натуральних чисел

Ділене : Дільник = Частка

Поділити число а на число b – це означає знайти таке число с, яке в добутку з числом b дає число а.

а : b = с с · b = а

Властивості:

Яким би не було число а, завжди

УВАГА!!!

Число а ділять на число b, коли хочуть зменшити число у b разів або з’ясувати, у скільки разів а більше за b.

Від збільшення діленого (дільника) у кілька разів частка збільшується (зменшується) у стільки ж разів.
Від збільшення діленого і дільника у кілька разів частка не зміниться.
Якщо числа а і b діляться на с, то

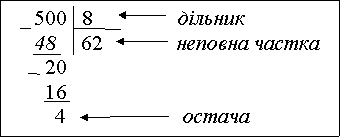
§ 14. Ділення з остачею

500 = 8 · 62 + 4

Щоб знайти ділене при діленні з остачею, треба неповну частку помножити на дільник і до знайденого добутку додати остачу.

Якщо остачею нехтують, то неповну частку називають наближеною часткою.

500 : 8  62

Знак  - наближено дорівнює

500 : 8  62 - наближення з недостачею (частка – число таке, як неповна частка, остачею нехтують);

500 : 8  63 - наближення з надлишком (частка – число на одиницю більше від неповної частки ).

Буквенні вирази. Формули

Буквений вираз: букви, числа, дії, дужки.

Буквені вирази:

2 · а пишуть 2а; a · b пишуть ab.

Знак множення часто не пишуть!

п – натуральне число

п + 1 – наступне натуральне число

Число у буквеному виразі – коефіцієнт.

Формули - буквений вираз позначений однією буквою.

Формули:

для обчислення периметра квадрата: Р = 4а

для обчислення периметра прямокутника:

Р = 2(а + b)

для обчислення довжини шляху:

S = vt.

Порядок виконання дій у виразах

Дії першого ступеня – додавання та віднімання.

Дії другого ступеня – множення і ділення.

У виразах, що містять тільки додавання і віднімання, дії виконують у тому порядку як вони записані.
У виразах, що містять тільки множення і ділення, дії виконують у тому порядку як вони записані.
У виразах, що місять дії обох ступенів, першими виконують множення і ділення, а потім додавання і віднімання.
У виразі з дужками спочатку виконують дії в дужках, а потім інші дії у встановленому порядку.
Якщо у дужки взято вираз, що містить дії обох ступенів, тоді і в дужках виконують дії за відомим порядком.

§16. Рівняння

Рівність, яка містить невідоме число, позначене буквою, називається рівнянням.

х + 3 = 10

Корінь рівняння – значення невідомого, при якому рівняння перетворюється на правильну рівність.

Рівняння: один корінь х + 3 = 10; х = 7.

два корені х + 15 : х = 8; х = 3, х = 5.

немає коренів х + 7 = 3.

Розв’язати рівняння означає знайти всі його корені або показати, що їх немає.

Правила розв’язування рівнянь:

Щоб знайти невідомий доданок, треба від суми відняти відомий доданок.
Щоб знайти невідомий від’ємник, треба від зменшуваного відняти різницю.
Щоб знайти невідоме зменшуване, треба до різниці додати відомий від’ємник.
Щоб знайти невідомий множник, треба добуток поділити на відомий множник.
Щоб знайти невідоме ділене, треба частку помножити на відомий дільник.
Щоб знайти невідомий дільник, треба ділене поділити на відому частку.

Розв’язування рівнянь

а + х = с

або

x + b = с

Знаходження невідомого доданка:

х = с – а

х = с – b

a – x = c

Знаходження невідомого від’ємника:

х = а – c

x – b = c

Знаходження невідомого зменшуваного:

х = с + b

a ∙ x = c

або

x ∙ b = c

Знаходження невідомого множника:

х = с : а

х = с : b

a : x = c

Знаходження невідомого дільника:

х = а : с

x : b = c

Знаходження невідомого діленого:

х = с ∙ b

§17. Типи задач та способи їх розв’язання

Сума	Різниця	Добуток	Частка
додавання	віднімання	множення	ділення

Збільшити на	Зменшити на	Збільшити у	Зменшити у
додавання	віднімання	множення	ділення

Відстань (шлях, S, км)	швидкість · час
Швидкість (, км/год)	відстань : час
Час (t, год)	відстань : швидкість

При зустрічному русі	швидкість зближення = сумі швидкостей
При русі в протилежних напрямах	швидкість віддалення = сумі швидкостей
При русі в одному напрямі	швидкість зближення або віддалення = різниці швидкостей

Швидкість за течією	= власна швидкість + швидкість течії
Швидкість проти течії	= власна швидкість – швидкість течії
Власна швидкість	= (швидкість за течією + швидкість проти течії) : 2
Швидкість течії	= (швидкість за течією - швидкість проти течії) : 2

Пряма. Промінь. Відрізок. Вимірювання відрізків

А пряма В

початку немає кінця немає

А промінь О

початок кінця немає

А відрізок В

початок кінець

Властивості:

Через дві точки можна провести тільки одну пряму;
Довжина відрізка дорівнює сумі довжин її частин;
Довжину відрізка виражають за допомогою іменованого числа;
Щоб знайти довжину відрізка, треба звести довжини його частин до однієї одиниці вимірювання і отримані значення додати.
Рівні відрізки мають рівні довжини.
Із двох відрізків більший той, довжина якого більша.

Відстанню між двома точками називається довжина відрізка з кінцями в цих точках.

Координатний промінь

О А В

0 1 3 6

Одиничний відрізок

Координатний промінь - промінь з вибраним одиничним відрізком та поділками, яким відповідають послідовні натуральні числа.

Координата точки – число, яке відповідає точці на координатному промені.

О(0), А(3), В(6)

Шкала – координатний промінь, лінійка, годинник,

спідометр.

Шкала – scala – драбина.

Кути та їх вимірювання

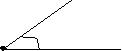А  АОВ,  ВОА,  О

О В

Кут – геометрична фігура, утворена двома променями, які виходять з однієї точки.

Промені – сторони кута, точка – вершина кута

ОА, ОВ – сторони кута, О – вершина кута

Порівняння кутів:

з двох кутів більшим є той, міра якого більша;
два кути будуть рівними, накладанням їх можна сумістити.

А О В

розгорнутий кут = 180º

Транспортир – прилад для вимірювання кутів.

Бісектриса - промінь, який виходить з вершини

кута і поділяє його пополам.

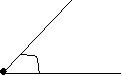
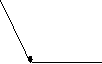
гострий < 90º прямий = 90º тупий > 90º

Трикутник та його види

Трикутник – окремий вид многокутника.

Має 3 вершини, 3 сторони, 3 кути.

Види трикутників (за сторонами):

різносторонній – всі сторони різні;
рівнобедрений – дві сторони рівні;
рівносторонній – всі сторони рівні.

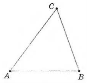
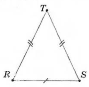
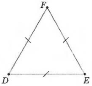
різносторонній рівнобедрений рівносторонній

Рівнобедрений трикутник має дві рівні бічні сторони, а третя – основа.

Периметр трикутника:

Р = а + b + с, де а, b, с – сторони

Периметр рівностороннього трикутника:

Р = 3а, де а – сторона

Види трикутників (за кутами):

гострокутний – всі кути гострі;
прямокутний – один кут прямий;
тупокутний – один кут тупий.

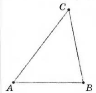
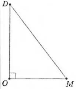
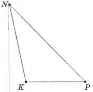
гострокутний прямокутний тупокутний

Два трикутники рівні, якщо вони суміщаються накладанням.

Властивість рівних трикутників: у рівних трикутників рівні відповідні сторони і відповідні кути.

Многокутники

AKBLCN – многокутник

Точки A, K, B, L, C, N – вершини

Відрізки – сторони

Суміжні сторони – дві сторони, що мають спільну вершину.

Дві суміжні сторони утворюють кут многокутника.

Многокутники

трикутник чотирикутник п-кутник

Периметр многокутника – сума довжин усіх сторін.

Формули для знаходження периметра:

многокутника: Р = па, де п – кількість вершин, а – сторона;
прямокутника: Р = 2(а + b), де а і b – сторони прямокутника;
квадрата: Р = 4а, де а – сторона квадрата.

Дві фігури називають рівними, якщо їх можна сумістити накладанням.

Площа прямокутника і квадрата

Одиничний квадрат – квадрат, сторона якого дорівнює одиниці довжини.

Одиниці площі: 1 мм², 1 см², 1 дм², 1 м²

1 ар = 100 м²; 1 га = 10 000 м²

Визначити площу фігури – означає дізнатися, скільки одиничних квадратів вміщується в даній фігурі.

Площа прямокутника = довжину помножити на ширину.

Площа квадрата = квадрату його стороні

Властивості:

Рівні фігури мають рівні площі.
Площа фігури дорівнює сумі площ її частин.

Прямокутний паралелепіпед. Куб. Піраміда

Прямокутний паралелепіпед – має три виміри: довжину (a), ширину (b) і висоту (c); 6 граней, 12 ребер і 8 вершин, всі грані – прямокутники.

Сума довжин усіх ребер прямокутного паралелепіпеда з ребрами a, b і c

Площа поверхні прямокутного паралелепіпеда = сумі площ його граней.

Куб – прямокутний паралелепіпед, у якого всі грані – квадрати. Ребра – рівні (а).

Сума довжин усіх ребер куба з ребром a

Площа поверхні куба = сумі площ його граней.

Піраміда – має основу (многокутник), вершину піраміди, бічні грані – трикутники.

Види пірамід: трикутна (основа – трикутник), чотирикутна (основа – чотирикутник), п-кутна (основа – п-кутник)

§ 21. Об’єм прямокутного паралелепіпед і куба

Одиничний куб – куб, ребро якого дорівнює одиниці довжини.

Об’єм прямокутного паралелепіпеда = дорівнює добутку його ребер.

Об’єм куба = кубу його ребер.

Властивості:

Рівні прямокутні паралелепіпеди мають рівні об’єми.
Об’єм прямокутного паралелепіпеда дорівнює сумі об’ємів його частин.

Одиниці об’єму: 1 літр = 1 дм³

м³

дм³

см³

1000

дм³

см³

мм³

Дробові числа і звичайні дроби

Звичайний дріб =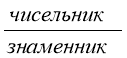

Знаменник - показує, на скільки рівних частин

поділено одне ціле.

Чисельник - показує, скільки рівних частин

взято.

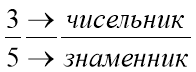
Правильний дріб: чисельник < знаменник

Правильний дріб < 1

Неправильний дріб: чисельник  знаменник

Неправильний дріб > правильний дріб

Неправильний дріб  1

Порівняння дробів:

Із двох дробів з однаковими знаменниками той дріб більший, в якого чисельник більший.

§ 24. Дроби і ділення

Частку від ділення двох натуральних чисел можна подати у вигляді звичайного дробу.

7 = ; 15 : 4 =

Мішане число – ціла і дробова частина.

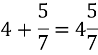
Правило виділення цілої частини з неправильного дробу.

Щоб виділити цілу частину з неправильного дробу, треба:

1) чисельник поділити на знаменник;

2) частку записати як цілу частину мішаного числа;

3) у чисельник дробової частини записати остачу від ділення;

4) знаменник залишити без зміни.

Правило перетворення мішаного числа в неправильний дріб.

Щоб перетворити мішане число у неправильний дріб, треба:

1) знаменник дробу помножити на цілу частину дробу і до результату додати чисельник дробу, отриману суму записати в чисельник.

2) знаменник залишити без зміни.

Додавання і віднімання дробів з однаковими знаменниками

Щоб додати дроби з однаковими знаменниками, треба додати їх чисельники і залишити той самий знаменник.

Щоб відняти дроби з однаковими знаменниками, треба знайти різницю їх чисельників і залишити той самий знаменник.

Правила:

Які б не були натуральні числа a, b i c, завжди

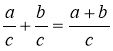i 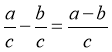при а > b

. Доповнення правильного дробу до одиниці. Віднімання дробу від натурального числа

Щоб знайти доповнення правильного дробу до одиниці, треба знайти різницю числа 1 і правильного дробу.

Наприклад:

Щоб відняти дріб від натурального числа, треба записати натуральне число у вигляді неправильного дробу зі знаменником, як у даного дробу, виконати віднімання дробів та виділити цілу частину, якщо це потрібно.

Наприклад:

§ 28. Додавання і віднімання мішаних чисел

Щоб додати два мішані числа, треба спочатку додати цілі частини, а потім дробові.

Щоб відняти два мішані числа, треба спочатку відняти цілі частини, а потім дробові.

Щоб відняти від цілого числа мішане, треба записати ціле число у вигляді мішаного із знаменником, як у даного мішаного числа і знайдені мішані числа відняти.

§ 29. Десяткові дроби

Звичайні дроби

Десяткові дроби

0,1

1,9

0,21

3,456

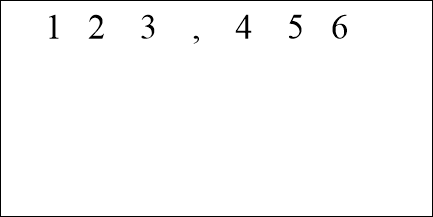
Сто двадцять три цілих чотириста п’ятдесят шість тисячних

Довідкова таблиця

	км	м	дм	см	мм
км		1000	10000	100000	1000000
м	0,001		10	100	1000
дм	0,0001	0,1		10	100
см	0,00001	0,01	0,1		10
мм	0,000001	0,001	0,01	0,1

Десятковий дріб = ціла частина , дробова частина

Дробова частина < одиниці

Увага! У десятковому дробі після коми має стояти стільки цифр, скільки нулів у знаменнику відповідного звичайного дробу.

ПРАВИЛО 1

$C:\Documents and Settings\Admin\Рабочий стол\Рисунок1.png$ Із двох десяткових дробів більший той, у якого ціла частина більша. Якщо цілі частини дробів рівні, то більший той, у якого десятих більше. Якщо ж і десятих порівну, то більший той, у якого більше сотих і т. д.

3,25 > 2,16; 3,25 > 3,16; 3,25 < 3,26;

ПРАВИЛО 2

До десяткового дробу справа можна дописувати один або кілька нулів. Якщо десятковий дріб закінчується нулями, з дробової частини їх можна відкинути.

5,20 = 5,2

ПРАВИЛО 3

Будь-яке натуральне число можна записати у вигляді десяткового дробу, написавши після нього кому і кілька нулів після коми.

4 = 4,0

§ 30. Додавання десяткових дробів

ПРАВИЛО ДОДАВАННЯ

Щоб додати два десяткових дроби, треба підписати доданки так, щоб кома була під комою, цілі – під цілими, десяті – під десятими, соті – під сотими і т. д. і виконати додавання.

1,23 2,50

4,56 0,23

5,79 2,73

Увага! Якщо доданки мають різну кількість десяткових знаків, то можна їх зрівняти, приписуючи нулі.

ЗАКОНИ ДОДАВАННЯ

Які б не були числа а, b і с, завжди:

переставний сполучний

§ 30. Віднімання десяткових дробів

ПРАВИЛО ВІДНІМАННЯ

Щоб відняти два десяткових дроби, треба підписати зменшуване і від’ємник так, щоб кома була під комою, цілі – під цілими, десяті – під десятими, соті – під сотими і т. д. і виконати віднімання.

5,23 2,50

4,11 0,23

1,12 2,27

Увага! Якщо у зменшуваному після коми цифр менш, ніж у від’ємнику, або навпаки, то справа приписують нулі.

Відняти від числа а число b означає знайти таке число с, яке в сумі з числом b дає число а.

а - b = с  с + b = а

§ 31а. Множення десяткових дробів

ПРАВИЛО МНОЖЕННЯ

Щоб перемножити два десяткових дроби, треба перемножити їх, не звертаючи увагу на коми, а в добутку відокремити комою справа стільки цифр, скільки їх є після коми в обох множниках разом.

Увага! Коли в добутку менше цифр, ніж треба відокремити комою, то спереду пишуть потрібну кількість нулів.

1,5 1,5

2,4 0,024

6 0 6 0

3 0 3 0

3,6 0 0,0 3 6 0

Закони множення

переставний

сполучний

розподільний

§ 31б. Окремі випадки множення десяткових дробів

ПРАВИЛО 1

Щоб помножити десятковий дріб на 10, 100, 1 000, 10 000, треба в цьому дробі перенести кому вправо відповідно на одну, дві, три, чотири цифри.

Увага! Якщо цифр не вистачає, то справа дописують потрібну кількість нулів.

0,012 · 10 = 0,12; 0,012 · 100 = 1,2;

0,012 · 1 000 = 12;

ПРАВИЛО 2

Щоб помножити десятковий дріб на 0,1; 0,01; 0,001; 0,0001, треба в цьому дробі перенести кому вліво відповідно на одну, дві, три, чотири цифри.

1,2 · 0,1 = 0,12; 1,2 · 0,01 = 0,012;

1,2 · 0,001 = 0,0012;

Увага! При множенні будь-якого числа на одиницю це число не змінюється.

§ 32а. Ділення десяткового дробу на натуральне число

ПРАВИЛО ДІЛЕННЯ

Щоб поділити десятковий дріб на натуральне число, треба поділити їх, не звертаючи увагу на коми, а в частці поставити кому, коли закінчено ділення цілої частини.

Увага! Якщо ціла частина діленого менша від дільника, то ціла частина частки дорівнює 0.

12,5 : 5 = 2,5; 1,25 : 5 = 0,25.

ПРАВИЛО

Щоб поділити десятковий дріб на 10, 100, 1 000, 10 000, треба в цьому дробі перенести кому вліво відповідно на одну, дві, три, чотири цифри.

Увага! Поділити число на 10, 100, 1 000, 10 000 – це те саме, що помножити його відповідно на 0,1; 0,01; 0,001; 0,0001.

ПРАВИЛО

Ділити одне натуральне число на друге, якщо ділене менше дільника, можна так, як ділять десятковий дріб на натуральне число, записавши ділене у вигляді десяткового дробу.

2 : 5 = 0,4; 10 : 50 = 0,2

§ 32б. Ділення десяткових дробів

ПРАВИЛО ДІЛЕННЯ

Щоб поділити число на десятковий дріб, треба в діленому й дільнику перенести кому вправо на стільки цифр, скільки їх є після коми в дільнику, а потім виконати ділення на натуральне число.

Увага! Якщо в діленому після коми менше цифр, ніж у дільнику, то до нього дописують потрібну кількість нулів.

ПРАВИЛО

Яким би не було число а, завжди:

а : 0,1 = а · 10;

а : 0,01 = а · 100;

а : 0,001 = а · 1 000.

ПРАВИЛО

Щоб знайти число за його десятковим дробом, треба число, що відповідає даному дробу, поділити на цей десятковий дріб.

§ 33. Округлення чисел

26 : 6 = 4,333…

26 : 6  4,333 – наближене значення частки,

округлене до тисячних;

26 : 6  4,33 – наближене значення частки,

округлене до сотих;

 наближено дорівнює

Увага! Округлюючи число, припускаються якоїсь похибки. Потрібно, щоб похибка була найменшою.

ПРАВИЛО ОКРУГЛЕННЯ

Якщо перша з відкинутих цифр 0, 1, 2, 3, 4, то останню цифру, що залишається, не змінюють.

Якщо перша з відкинутих цифр 5, 6, 7, 8, 9, то останню цифру, що залишається, збільшують на 1.

16,42  16,4; 16,46  16,5;

Увага! Якщо округлюють натуральне число, то замість відкинутих цифр ставлять нулі.

26413  26400; 26475  26500;

§ 34. Відсотки

Відсоток (процент) – це одна сота частина.

1 к. = грн. 1 к. – 1% грн.

1 кг = ц 1 кг – 1% ц

1 см = м 1 см – 1% м

1 а = га 1 а – 1% га

ПРАВИЛО Щоб записати відсотки десятковим дробом або натуральним числом, потрібно число, яке стоїть перед знаком %, поділити на 100.

Наприклад: 35 % = 35 : 100 = 0,35

ПРАВИЛО Щоб виразити число у відсотках, потрібно його помножити на 100 %.

Наприклад: 0,12 = 0,12 · 100 % = 12 %

Проміле – тисячна частина числа

Проба – кількість грамів дорогоцінного металу у 1 000 г.

§ 35. Задачі на відсотки

Задачі І типу: знаходження

відсотків від числа

ПРАВИЛО

Щоб знайти відсоток від числа, треба дане число поділити на 100 і результат помножити на кількість відсотків.

Наприклад:

Знайти 20% від числа 300.

300 : 100 · 20 = 60.

Задачі ІІ типу: знаходження числа

за його відсотками

ПРАВИЛО

Щоб знайти число за його відсотком, треба дане число поділити на кількість відсотків і результат помножити на 100.

Наприклад:

Знайти число, 30% якого становить 60.

60 : 30 · 100 = 200.

§ 36. Середнє арифметичне. Середнє значення величин

ПРАВИЛО

Середнє арифметичне кількох чисел дорівнює сумі цих чисел, поділеній на їх кількість.

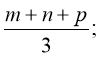- середнє арифметичне трьох чисел

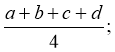- середнє арифметичне чотирьох чисел

Увага! Якщо сума п чисел дорівнює S, то їх середнє арифметичне дорівнює S : п.

Середні значення величин:

Щоб знайти, скільки у середньому долає за годину учасник руху, треба обчислити середнє арифметичне відстаней на різних ділянках шляху.
Щоб знайти середній відсоток, треба обчислити середнє арифметичне заданих відсотків.

Середня оцінка розробки

Структурованість

5.0

Оригінальність викладу

5.0

Відповідність темі

5.0

Загальна:

5.0

Всього відгуків: 1

Оцінки та відгуки

Матвійчук Сергій Анатолійович 17.02.2019 в 21:38

Добре

Загальна:

5.0

Структурованість

5.0

Оригінальність викладу

5.0

Відповідність темі

5.0