ПЛАН

 

 

1.            Анотація.                                                                                                     3-4

2.            Основна частина.                                                                                       5-33

2.1.            Основні теоретичні відомості.                                                        5-14

2.1.1.     Урок як основна форма організації навчання.                   5-6                

2.1.2.     Нестандартний урок як форма організації навчання.        6-11              

2.1.3.     Роль гри та нестандартних уроків у підвищенні                              інтересу учнів до вивчення математики.                         12-14

2.2.            Практична частина.                                                                         15-29

2.2.1.     Методичні рекомендації  щодо технології реалізації  

          Ідеї (із досвіду роботи).                                                        15-21

2.2.2.     Приклади проведення нестандартних уроків та 

                            фрагменти використання ігрових методів на уроках                             з метою підвищення інтересу учнів до вивчення 

                           математики.                                                                           22- 36            

2.3.            Додатки.                                                                                           37- 47

2.3.1.     Додатки до уроку  по темі «Логарифмічна функція.       

Розв’язування логарифмічних рівнянь та   нерівностей».          37-43             

2.3.2.     Запитання командам до гри «Далі, далі…»                           44

2.3.3.     Малюнки до  теми «Перпендикуляр і похила».                   45

2.3.4.     Асоціативний кущ.                                                                              46

2.3.5.     Юридична шпаргалка.                                                                         46

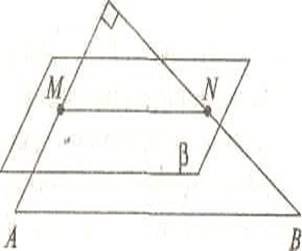
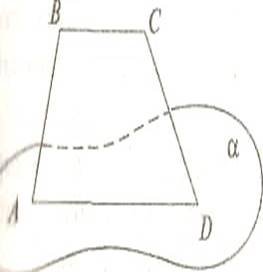
2.3.6.     Малюнки до  теми «Взаємне розміщення прямих і 

                 площин у просторі».                                                                           47

3.            Висновки.                                                                                                   48-49 4. Список використаних джерел.                                                                    50

 

 

 

Анотація.

Предмет математика настолько серьезен,  что полезно не упускать случаев  делать его немного занимательным.  (Блез Паскаль)

    Сучасна освіта — це освіта для людини. Її стрижнем є розвиваюча, культуротворча домінанта, виховання здатності до самоосвіти і саморозвитку особистості, яка вміє використовувати набуті знання і вміння для творчого розв'язання проблем, критично мислити, опрацьовувати різноманітну інформацію, прагне змінити на краще своє життя.

    Роль викладача є вирішальною у процесах формування мислення, гартування характеру й виховання моральних якостей учня. Він генератор і джерело ідей, якими керується другий суб'єкт педагогічного процесу — учень. Від педагогічної майстерності викладача залежить націлювання учнів на належний навчальний лад. Тоді цілі викладача стають і цілями учнів — у них одна мета. Природно, що прагнення обох до єдиної мети прискорює її досягнення. Щоб керувати процесом формування і розвитку здібностей учнів, треба знати актуальні і потенціальні їх рівні. Водночас виникає проблема: якими повинні бути умови середовища, щоб кожен учень міг розвинути свої творчі нахили й перетворити їх у творчі досягнення. 

     Працюючи 20 років у ліцеї та спостерігаючи за учнями, можна дійти висновку, що для багатьох учнів визначальним чинником вивчення математики є її загальновизнана роль у житті та інших науках. Але є учні, які на уроці перестають слухати або, навпаки, тільки роблять вигляд, що слухають, але не чують, якщо новий матеріал їх не зацікавив з самого початку. Запобігаючи байдужості на уроці, появу нового матеріалу потрібно підпорядковувати природній допитливості учня: новий факт не виникає з «нічого»; разом з дітьми з'ясувати можливості його застосування, а форму організації навчання обирати оптимальною. Отже, завдання, яке постало перед викладачем, — збудити здібності своїх учнів, виховати в них сміливість думки і впевненість у тому, що вони розв'яжуть кожну задачу, в тому числі й творчого характеру, — без особистого захоплення справою, без наявності педагогічного такту і таланту, без умілого вибору форм навчання, методів, прийомів та засобів втілити в життя неможливо. 

    Особистісно зорієнтоване навчання передбачає навчальний процес, за якого як учні, так і викладачі почувають себе комфортно. Я, як і, мабуть, кожний викладач, отримую задоволення від роботи, коли бачу позитивні наслідки своєї праці, учні — також. Однією з причин, що допомагають отримати найкращі результати, є вибір оптимальної форми навчання. Традиційні форми навчання математики іноді заважають здібному учню повністю проявити себе, тому один зі шляхів подолання цього я вбачаю у використанні нестандартних форм організації навчання. 

    Тому об’єктом дослідження у цій роботі виступає нестандартне викладання математики, а предметом дослідження є процес нетрадиційного навчання на уроках математики. 

    У рамках викладання математики можуть бути використані при розробці конспектів нетстандартних уроків. 

Гіпотеза дослідження полягає в наступному: якщо застосовувати на уроках математики нестандартні форми навчання, то це буде сприяти: 

Ø  формуванню в учнів таких якостей особистості, як самостійність, колективізм, уміння планувати свою роботу, передбачати результати праці, відповідальності за наслідки своєї діяльності, організаторських і комунікативних здібностей; 

Ø  мотивації підростаючого покоління до ефективної трудової й навчальної діяльності; 

Ø  підвищення інтересу учнів до навчання. 

Ціль роботи: визначити роль гри та нестандартних уроків у підвищенні інтересу учнів до вивчення  математики. 

Основні теоретичні відомості.

Урок як основна форма організації навчання.

    Основною організаційною формою навчання в сучасній освіті є урок.  Урок — форма організації навчання, за якої заняття проводить викладач з групою учнів постійного складу, одного віку й рівня підготовки впродовж певного часу й відповідно до розкладу. 

    Урок має такі особливості: 

üє завершеною та обмеженою в часі частиною навчального процесу, під час якого розв'язуються певні навчально-виховні завдання; 

üкожен урок включається в розклад і регламентується в часі та за обсягом навчального матеріалу; 

üна відміну від інших форм організації навчання є постійною формою, що забезпечує систематичне засвоєння учнями знань, умінь і навичок; 

üвідвідування уроків обов'язкове для всіх учнів, тому вони вивчають систему знань, поділених поурочно, в певній логіці; 

üє гнучкою формою організації навчання, яка дає змогу використовувати різні методи, організовувати фронтальну, групову та індивідуальну навчальну діяльність учнів; 

üспільна діяльність викладача й учнів, а також спілкування великої сталої групи учнів (групи) створює можливості для згуртування колективу

дітей; 

üсприяє формуванню пізнавальних якостей особистості (активності, самостійності, інтересу до знань), а також розумовому розвитку учнів.      Кожен тип уроку має свою структуру, тобто склад (з яких елементів або етапів складається), послідовність (в якій послідовності ці елементи входять у заняття), зв'язок (як вони пов'язані між собою). 

    Отже, визначаючи структуру уроку, вчитель повинен враховувати тему і зміст, найдоцільніші методичні засоби і прийоми, конкретні умови, в яких проводитиметься урок, рівень підготовленості учнів тощо. 

    Вдосконалення урокувідбувається за такими аспектами: 

а)різноманітність видів уроків (урок ділова гра, урок пресконференція, урок КВК, урок-змагання, урок-консиліум, уроктвір, урок-винахід, урок-залік та ін.); 

б) максимальна щільність уроку; 

в) насиченість уроку різними видами пізнавальної діяльності; 

г) запровадження самостійної діяльності в роботі учнів; 

д) використання програмованого і проблемного навчання; 

е) здійснення міжпредметних зв'язків; 

ж) подолання перевантаженості учнів. 

    Цікавими для теорії і практики є власне нестандартні уроки. Суть їх полягає в такому структуруванні змісту і форм, яке викликало б насамперед інтерес в учнів і сприяло їхньому оптимальному розвитку і вихованню. До нестандартних уроків слід віднести інтегровані, міжпредметні, театралізовані, сугестопедичні, уроки з різновіковим складом учнів та інші.  

 

 

Нестандартний урок як форма організації навчання.

    Сьогодні в освітньому просторі України відбуваються кардинальні зміни, зумовлені процесом реформування школи, який відбувається відповідно до закону України «Про загальну середню освіту», Концепції загальної середньої освіти, Державного стандарту загальноосвітньої освіти. Все це забезпечує системне оновлення змісту та перехід на нову структуру навчання. В викладачів з’являється можливість застосовувати нові активні технології навчання, які цінні для кожного учня. 

    Наразі змінено підхід до визначення структури уроку. Дидакти наголошують на її багатоваріантному характері, пропонують розрізняти типові уроки та специфічні форми їх проведення. Визначення свободи викладача в доборі форми уроку (звичайно, з огляду на його мету, зміст, вікові особливості учнів) стимулює широке використання відомих форм та пошук нових. 

    Стандартні уроки відіграють значну позитивну роль у навчанні учнів. Вони охоплюють основні етапи навчального процесу: підготовка до вивчення теми, сприймання й осмислення теми, сприймання й осмислення матеріалу, закріплення його різноманітними вправами; перевірка, оцінювання знань, умінь і навичок; узагальнення й систематизація знань. 

    Проте вже в середині 70-х років минулого століття з’явилася тенденція до зниження інтересу дітей до класних занять. На практиці це реалізувалося появою нестандартних (нетипових) уроків, головною метою яких є обудження інтересу учнів до навчальної праці. 

    Суть нестандартних уроків досліджували багато педагогів, методистів. Зокрема на думку О. Антипової, В. Паламарчук, Д. Румянцевої, суть нестандартного уроку полягає в такому структуруванні змісту і форми, яке б викликало насамперед інтерес учнів і сприяло їхньому оптимальному розвитку й вихованню. Л. Лухтай називає нестандартним такий урок, який не вкладається (повністю або частково) в межі виробленого дидактикою, на якому викладач не дотримується чітких етапів навчального процесу, методів, традиційних видів роботи. Е.Печерська бачить головну особливість нестандартного уроку у викладанні певного матеріалу у формі, пов’язаній з численними асоціаціями, різними емоціями, що допомагає створити позитивну мотивацію навчальної діяльності О.Митник і В. Шпак наголошують, що нестандартний урок народжується завдяки нестандартній педагогічній теорії, вдумливому самоаналізу діяльності викладача, передбаченню перебігу тих процесів, які відбуваються на уроці, а найголовніше – завдяки відсутності штампів у педагогічній технології. 

    Головною в роботі викладача стала проблема зробити навчання цікавим: для учня це означає посильним і успішно-результативним, для викладача — радісним. Творчо працюючи, він завжди прагне:   пропонувати посильний рівень вимог відповідно до рівня навченості

та научуваності;   вчити учнів концентруватися та максимально викладатися в обмежений час; 

 дати можливість навіть слабкому учневі отримати високу оцінку;   створювати умови для свідомого і самостійного вибору учнями рівня засвоєння навчального матеріалу; 

 дати можливість сильним учням проявити свої творчі здібності.      Адже інтерес до діяльності має спеціальну здатність підвищувати працездатність, включаючи увагу. Підтримання бажання вчитися вимагає зміни способів і форм сприйняття нового, створення різних ситуацій для застосування вивченого. Виховання ж інтересу передбачає реалізацію багатьох методичних прийомів, пошук і застосування різних технологій навчання, а головне — невтомну вчительську працю, самовдосконалення і самоосвіту. 

    Систему своїх уроків треба намагатися побудувати так, щоб учні працювали з повною віддачею сил, з інтересом. Учням подобаються завдання творчого характеру, які розвивають у них пізнавальний інтерес: складання казок, кросвордів, ігор; виконання творчих робіт; участь у математичних змаганнях.                

    Готуючись до уроків, викладач повинен дотримуватися таких правил:

 Урок має бути продуманим до дрібниць, щоб його етапи логічно випливали один з одного, а учні розуміли, чому, що і за чим вони роблять на занятті. 

 Корисно діяти за принципом «Краще один раз побачити, ніж сто разів почути». Усе, що викладач говорить, бажано втілювати в зримі образи. Наочність має бути динамічною, щоб показати невидиме: хід міркувань, зв'язок між поняттями. 

 Учнів потрібно ретельно готувати до усвідомлення теми уроку, а не записувати її наперед. 

 На уроці повинно бути цікаво. Адже без емоцій, без переживань розум не напружується. Зацікавленість виникає там, де викладачу вдається захопити дітей своєю емоційністю. 

    Велику увагу необхідно приділяти розвитку уяви, нестандартного мислення і фантазії учнів. Тому уроки можуть бути грою, змаганням з появою казкових героїв. Залежно від теми, мети та групи, в якій проходить урок, проводити уроки-лекції, уроки-практикуми, уроки систематизації та узагальнення знань у формі подорожей, конкурсів, математичних змагань. Адже, передусім, важливими є умови для створення творчої атмосфери, самокерування, взаємодопомоги і взаємоконтролю. Саме нестандартні уроки сприяють розвитку творчих здібностей дітей, виховують навички дослідницької діяльності, дають високий ефект практичної спрямованості матеріалу, що, зрештою, приводить до глибокого розуміння предмета, зацікавленості ним. Але само собою зрозуміло, що розумову самодіяльність, тямущість не можна ні «втокмачити», ні «вкласти» в чиюсь голову. Практика показала, що результати надійні лише тоді, коли введення в деяку галузь знань відбувається в легкій, приємній і ненав'язливій формі, на цікавих і дотепних прикладах, в ігровій формі. Крім того, в такій формі навчання є більш захоплюючим, доступним. Як правило, ігрову форму уроку діти сприймають з найбільшим захопленням і працюють здружено та натхненно. Взагалі, така форма роботи є продуктивною і викликає в учнів значно більший інтерес та ентузіазм. Але яким би за формою чи змістом не був урок, головним у ньому є праця — організована, результативна, творча. Кожен такий урок стає уроком, якого чекають, на якому учні відчувають радість творчої праці, де виховання досягається не штучно, не мимохідь, а послідовно і логічно через навчання. Урок вважається результативним, якщо учні глибоко усвідомили і «привласнили» мету викладача, коли вона глибоко перетворилася в їхнє особисте прагнення, бо сучасний урок — це урок демократичний, глибоко продуманий, організований і керований, що проводиться не для учнів, а разом з ними, з урахуванням дитячих можливостей, потреб та інтересів. Одним словом, на уроці не може бути об'єктів і суб'єктів. Лише суб'єкти — по обидва боки вчительського столу.     

Таким чином, дитину спочатку потрібно навчити хотіти й любити, а вже потім

— знати і вміти. Як ми бачимо все це здійснюється за допомогою нестандартних уроків. 

    Сьогодні нестандартний урок – це імпровізоване навчальне заняття, що не

має традиційної структури. Такі уроки не вкладаються (повністю або частково) в рамки виробленого і сформованого дидактикою. Викладач не дотримується чітких етапів навчального процесу, традиційних методів, видів роботи. В сучасних умовах особливість нестандартних уроків полягає в такому структуруванні змісту і форми, яке б викликало зацікавлення в учнів, сприяло їхньому оптимальному розвитку й вихованню. Для нестандартних уроків характерною є інформаційно-пізнавальна система навчання – оволодіння готовими знаннями, пошук нових даних, розкриття внутрішньої сутності явищ через диспут, змагання. На цьому уроці викладач може організувати діяльність групи так, щоб учні в міру можливості працювали самостійно, а він керував цією діяльністю, забезпечуючи її необхідними матеріалами. Порівняно із звичайним, нормативним заняттям нестандартний урок максимально стимулює пізнавальну активність та ініціативу учнів. Навчання на ньому спрямоване на підвищення якості їхніх знань, формування працьовитості, цілеспрямованості, потрібних у житті навичок і вмінь. Крім цього такі уроки більше подобаються учням, ніж буденні навчальні заняття. Насамперед тому, що навчальний процес тут має багато спільного з ігровою діяльністю дітей. Майже всі прийоми, способи дії нестандартних уроків відзначаються ігровим спрямуванням. Недивно, що в методичній літературі їх часто визначають як «урок-гра», «урокзмагання» тощо. 

    Нестандартний урок стимулює пізнавальну самостійність, творчу активність, ініціативу учнів, сприяє їх розвитку, підвищенню якості знань, формуванню працьовитості, потрібних у житті навичок та вмінь. Вони виникли порівняно недавно під впливом засобів масової інформації (телебачення, радіо).      З метою удосконалення навчального процесу бажано використовувати нетрадиційні форми навчання, або їх елементи. Застосування нетрадиційних форм навчання сприяє формуванню пізнавальних інтересів учнів. Нестандартні уроки поділяють на такі типи: 

 

Роль гри та нестандартних уроків у підвищенні  інтересу учнів до вивчення математики

 

    Відомо, що діти йдуть до школи за спілкуванням з друзями, з викладачем. Найбільшу радість і задоволення вони отримують від роботи на уроці, що дозволяє відкрити себе і свої задатки, здібності тощо. Очі дітей загоряються у той момент, коли їх навчають чомусь значному, важливому в житті, а не для отримання оцінок.

    Розкрити особистість учня можливо, якщо викладач йтиме на урок не тільки зі знанням навчального матеріалу, методів і прийомів навчання, набором красивих задач і вмінням їх майстерно розв'язувати, а й із різноманітними і цікавими способами і прийомами організації праці учнів. Багато традиційних методів викладання на сьогоднішній день малоефективні і не допомагають розвивати інтерес до вивчення математики.    Ігрові    методи    і    форми    навчання    суттєво відрізняються  від  традиційних  тим,   що  дають  змогу  учню безпосередньо стати учасником ситуації чи події.

    Розвиток науки і техніки дав викладачам і учням нові форми комунікації, нові типи вирішення абстрактних і конкретних завдань, нові технології навчання. 

    Процес навчання потребує напруженої розумової роботи дитини і її власної активної участі в цьому процесі. Пояснення і демонстрація, самі по собі, ніколи не дадуть справжніх, стійких знань. В. Гейне писав: «Кажуть, що посередині між двома протилежними думками лежить істина. В жодному разі! Між ними лежить проблема». Отже перед нами – проблема. Як викладати математику, щоб в учнів не втрачалась зацікавленість до предмета? Відповідь на це питання може бути одна – засоби інтерактивного навчання.     Умовна класифікація технологій інтерактивного навчання наступна:

ü  інтерактивні технології кооперативного навчання; 

ü  інтерактивні технології колективно-групового навчання; 

ü  ситуативне моделювання; 

ü  опрацювання дискусійних питань.

    Саме до технологій ситуативного моделювання відносять гру. У західній дидактиці поступово відходять від терміна «гра» і вживають поняття «симуляція», «імітація».

     На мою думку, майбутнє за системою навчання, що вкладається в схему «учень – технологія – викладач», де учень стає активним учасником процесу навчання. Навчально – ігрове спілкування несе на собі велике навантаження, оскільки виконує наступні функції:

ü  виховну    -    розкривається    почуття    колективізму, сміливості,   рішучості,   виховуються   морально-етичні якості;  üпізнавальну    -    розвиток    пізнавальної    активності,       збагачення навчальних досягнень новою інформацією;  

ü  гедонічну - переживаються раніше невідомі почуття, формується оптимальний життєрадісний настрій;

ü  компенсаторну - через гру знімається психогенне і фізичне напруження, підвищується загальний тонус, з'являється почуття розкутості.

    Тому ділові та імітаційні ігри знаходять широке застосування у найрізноманітніших сферах діяльності: економіці, політиці, екології, міському плануванні, освіті.

    Завдяки педагогічному моделюванню визначається ігрова форма й вид гри, відповідно до навчального матеріалу вибираються методи і прийоми, способи і засоби, що стимулюють навчання, тобто формують цілі, мотиви і сприяють вирішенню дидактичних завдань. При цьому учитель має змогу постійно здійснювати контроль, корекцію та оцінку пізнавальної діяльності учнів. Гра відображає зміст навчального матеріалу, що складає предмет діяльності, враховує вікові особливості учня. 

    Щоб зацікавленість учнів до вивчення математики не знижувалася, при вивченні теми «Види та способи розв’язування  показникових рівнянь» -  використовую урок – гру у формі змагання. Вивчаючи тему «Многогранники», розгадуємо та складаємо власні кросворди. Учн полюбляють гру «Хто швидше» (тема «Похідна функції»). На своїх уроках надаю перевагу парним іграм, саме вони покращують якість уроку, вміння шукати розв’язки та вирішення проблемних питань; розвивають логічне мислення.   Одним із активних методів, які я дуже часто використовую на своїх уроках є створення проблемної ситуації, яка впливає на краще засвоєння матеріалу учнями, розвиває їх уважність, наслідком чого є висока активність учнів на уроці.

    Розглядаючи навчально-ігрову діяльність як процес навчання, можна зробити висновок:

Øігрова   діяльність   -   це   багатокомпонентна   цілісна система;

Øспосіб досягнення цілей і розвиток особистості учнів відбувається        завдяки        особистісно-мотиваційній діяльності;

Øпізнавальна діяльність, що розгортається на основі гри, має свій предмет і спрямована на конкретні цілі й результати;

Øрезультат  ігрового   навчання  досягається   в   процесі поетапного вирішення системи проблемних завдань;

Øзавдяки ігровій діяльності формуються комунікативні дії учнів між собою та вчителем, підвищується рівень естетико-етичного боку навчання;

Øзростає інтерес до вивчення предмета.

 

 

 

 

 

 

 

 

Практична частина.

Методичні рекомендації  щодо технології реалізації ідеї.

     Відомо, що будь-який урок – це складне педагогічне явище, витвір викладача, на якому учні демонструють свої знання, уміння та навички. Чи цікаво дітям на уроці? Чи люблять вони вчитися? На ці питання неможна відповісти напевне. Іноді діти ідуть на урок із задоволенням, іноді без нього. Як зацікавити дітей? Як привернути їх увагу до свого предмету? Як донести матеріал до їх свідомості яскраво і красиво, щоб запам'яталось надовго і назавжди?

    Іноді можна почути, що математика складна, суха і нецікава наука. Математика сувора, але красива й глибока, як чиста криниця. А завдання викладача  полягає в тому, щоб розкривати перед учнями її емоційний бік, чуйну і вродливу стать. Як краще цього домогтися?  Красивими, цікавими уроками. Уроками, які пробуджують цікавість і працьовитість, фокусують увагу і зосередженість. Отже, цього можна досягти тільки на уроці проведеному в нестандартній формі.

    Під час проведення нестандартних уроків спостерігається велика зацікавленість учнів, вони активні, збуджені, працюють із задоволенням. Досвід роботи показує, що для поліпшення розуміння,закріплення та відтворення інформації доцільно проводити такі уроки як: урок – змагання; урок – вікторина; урок – "круглий стіл"; урок – гра; інтегровані уроки та ін..     У своїй роботі на уроках математики я використовую систему запитань, створюючи різного роду проблемні ситуації, або вносячи творчі елементи, завдяки чому учні отримають змогу активізувати розумову діяльність, зробити "відкриття".

    Другий напрямок реалізації творчої потреби дитини в умовах  навчання - це ігрова діяльність. У грі розвивається уява, утверджуються образи фантазії, виниклі ідеї, створюються продукти діяльності, які є для учня емоційно привабливими. Важливість гри у тому, що вона надає учневі можливість помріяти, проявити уяву, дає свободу самовияву і творчості. Використання нестандартних уроків математики створює сприятливі умови для організації колективної роботи різних вікових груп, що вчаться, і класів розширення кругозору учнів  за рахунок залучення їх до вивчення додаткового матеріалу.     Отже, я вбачаю у використанні нетрадиційних форм і методів навчання можливість зробити процес навчання цікавим, та всепоглинаючим. Створити у учнів робочий настрій. Допомогти подолати труднощі в засвоєнні навчального матеріалу. В сучасних умовах важливість нестандартного уроку полягає в тому, що він підвищує ефективність навчання, зацікавлює учнів до вивчення нового матеріалу. Порівняно із звичайним, нормативним заняттям, нестандартний урок максимально стимулює пізнавальну, творчу активність та ініціативу учнів. Навчання на ньому спрямоване на підвищення їхніх знань, формування працьовитості, цілеспрямованості, потрібних у житті навичок і вмінь.

 

    Приведу приклади деяких технологій, які використовую на своїх уроках:

 

№ п/п	Технології	Коли доцільно використовуват и	Що формує в учнів
1	Обговорення проблеми в загальному колі(«Мікрофон», «Незакінченні речення».	Під час вивчення складних або проблемних питань у навчальному матеріалі, мотивації пізнавальної діяльності, актуалізації опорних знань.	Сприяє розвитку вміння вільно висловлювати власні ідеї, розвиває вміння говорити коротко,але по суті й переконливо.
2	Навчаючись вчусь(«Броунівський рух», «Кожен учить кожного»).	Під час вивчення великого обсягу інформації, узагальненя та повторення вивченого.	Підвищує інтерес до предмета,формує вміння структурувати, узагальнювати, аналізувати матеріал.
3	Мозковий штурм.	Під час засвоєння вмінь та навичок, розвязування складних задач або для пошуку різних способів розвязування однієї  задачі.	Сприяє розвитку уяви та творчості, формує вміння чітко висловлювати свою думку.
4	Робота в парах.	Під час засвоєння, закріплення, перевірки знань	Сприяє розвитку навичок спілкування.
5	Два-чотири-всі разом.	Під час закріплення та засвоєння нового матеріалу з метою його грунтовного аналізу та осмислення.	Сприяє розвотку спілкування в групі.
6	Робота в малих групах( «Діалог», «Спільний проект», «Пошук інформації».	Підчас закріплення вмінь та навичок.Для розв’язання складних проблем,що потребують колективного розуму.	Сприяє розвитку вмінь аналізувати,узагальнювати ; розвитку пізнавальної активності, логічного мислення.
7	Карусель.	Під час інтенсивної перевірки обсягу й глибини наявних знань.	Розвиває вміння аргументувати власну позицію.
8	Акваріум	Під час закріплення вмінь та навичок.	Сприяє розвитку спілкування в малій групі, вдосконаленню вміння дискутувати та аргументувати свою думку.

 

    Розглянемо деякі інтерактивні методи, які я намагаюсь використовувати на своїх уроках:

 Мотиваційні інтерактивні методи навчання – це способи діалогічної взаємодії учнів, за допомогою яких кожен визначає власну позицію у ставленні до способів діяльності класу, окремих учнів, учителя, самого себе.

Серед цих методів можна виділити слідуючі:

а) «Інтерв’ю» 

Учні, працюючи в парах, ставлять запитання, які актуалізують знання з теми уроку, що обговорюється. Наприклад:

–        Що тобі відомо з теми?

–        Що нового ти дізнався, спілкуючись із учителем, однокласниками?

–        Які запитання виникли в тебе в ході вивчення теми?

Наступним етапом є обговорення відповідей на запитання інтерв’ю.

б) «Самооцінка» 

Учні називають позитивні та негативні моменти в організації та проведенні уроку. Тоді наступний урок рекомендовано розпочати з коментарів щодо виправлення помилок або покращення роботи на уроці, при цьому звернути увагу на ті недоліки, які були відмічені учнями.

в) «Мої очікування» 

Цей метод використовують перед вивченням нової теми або на початку навчального року чи семестру. Учні на мотиваційному або діагностичному етапі вивчення теми визначаються за такими напрямами:  Я очікую від себе… ; Я очікую від вчителя…; Я очікую від вивчення теми… . 

г) «3:2:1» 

Учні в письмовій або усній формі відзначають

ü3 моменти уроку, які їх зацікавили;

ü2 питання, які хотілось б поглибити;

ü1 момент, який вони будуть використовувати в майбутньому.

 

•      Пізнавальні інтерактивні методи навчання, метою яких є здобуття нових знань, їх систематизація, вдосконалення і т. д.

а) «Від А до Я»

Учням пропонується скласти словничок геометричних термінів на чотири вибраних літери: А; Б; В; Г; Д; Е; Є. Наприклад: терміни до теми

«Многогранники» або «Об’єми многогранників», «Тіла обертання» або

«Об’єми тіл обертання»…

б) «Ділова гра»

Для того щоб навчаючись гратися треба відпрацювати правила гри і чітко уявляти мету. Чим чіткіші і конкретніші правила, тим ефективнішим буде результат.

Ділова гра має таку схему:

üЕтап підготовки

-         розробка гри (сценарій, загальний опис гри, інструкції, матеріальне забезпечення);

-         введення до гри (повідомлення цілей, умови, правила, розподіл ролей, формування груп);

üЕтап проведення

-         групова робота;

-         міжгрупова дискусія;

üПідведення підсумків 

-         завершення гри;

-         аналіз гри;

-         оцінювання та самооцінювання роботи; - висновки та рекомендації.

    Гра може проходити у формі уроку або зайняти певну частину уроку. 

Приклад такого  уроку (тема «Показникова функція»), які я проводила в групах ІІ курсу, я наведу в слідуючому розділі.  Урок дуже сподобався учням та мав позитивні результати не тільки в навчанні але й в настрої учнів, що значно підвищило їх  інтерес до уроків математики.

•      Інформаційні інтерактивні методи навчання використовують з метою обміну інформацією стосовно теми чи розв’язання задачі. Пропоную розглянути один із таких методів, який має цікаву назву «Калейдоскоп».

Учні класу об’єднуються в невеликі групи. Кожна група одержує теоретичне завдання:

а) упродовж 5 хв учні вивчають теорію, обговорюють питання, що виникають під час вивчення;

б) далі вчитель, вибираючи з кожної групи по одному учню, формує нові групи, де зібралися учні, які вивчили різні теоретичні питання. За 20 хв кожен учень групи повинен розповісти членам утвореної групи те, що вивчив за перші 5 хв.

в) Останні хвилини уроку вчитель викликає по одному учню з цієї групи й опитує за вивченою темою, оцінюючи їх відповіді.

 

•      Евристичний  інтерактивний метод навчання «Мозковий штурм»:

üумови задачі формулюються в загальних рисах на початку;

üгрупа «генераторів» ідей пропонує максимальну кількість гіпотез за певний час. Висовують будь-які гіпотези – помилкові, фантастичні і т.

д. , вони повинні бути безперервні, доповнюватися і розвиватися. На кожне обговорення ідей відводиться до 2 хв (ідеї конспектують в зошитах);

üгрупа експертів оцінює запропоновані ідеї;

üякщо задачу в процесі «штурму» не розв’язано, то її можна запропонувати в зміненій формі; ü оцінювання гіпотез.

     Щоб розвинути пізнавальні і творчі здібності учнів, застосовую роботу в парах, використовуючи різноманітні способи утворення пар (один проти одного – із сусідом по парті – із тим, хто сидить позаду (спереду)), роботу в трійках, взаємне навчання. Використовую методику незакінчених речень,  «Мозковий штурм», «Мікрофон». Група починає працювати лише за умов, коли будуть успішно визначені обов'язки кожного з членів. Тому в ній обов'язково повинні бути лідер, хранитель часу, секретар і доповідач. Позитивним у створенні груп є те, що всі учні цілеспрямовано працюють над ситуативною проблемою, між учнями виникають розуміння один одного, бажання допомогти, підказати, підтримати. Учні, що мають низький рівень навченості, також стають активними учасниками процесу. Роль викладача – спрямувати роботу учнів, виявити рівень знань і вмінь, враховувати їх ідеї.

     Практикуючи роботу в групах на своїх уроках, я зрозуміла,  що створення груп одного рівня знань є доцільним у процесі вивчення нового матеріалу. Учні першої  та  другої груп займаються навчальними дослідженнями, третя і четверта групи  розв'язують типові задачі, розбирають готові розв'язки або користуються зразками аналогічних задач, а свій звільнений час спрямовую на роботу з учнями п'ятої групи: пояснення і опрацювання теорії, розв'язування простих  задач.

     Створення різнорівневих груп доцільніше на уроках закріплення вивченого матеріалу, коли, опитавши кращих учнів, я  можу доручити їм підготувати до відповіді інших, розібрати готову задачу, пояснити її іншим учням тощо. Наприклад, на уроках формування знань та вмінь учні працюють у групах (4-6 чоловік)  різних рівнів. Кожна група за певний час повинна розв'язати задачу. Після того як час закінчився, представник групи захищає ідеї розв'язання задачі. Отримана ним оцінка, у виставленні й обґрунтуванні  якої бере участь вся група, ставиться всім членам групи. Оскільки члени групи не знають наперед, хто з них відповідатиме, то вони зацікавлені, щоб кожен був добре підготовлений, і це стимулює їхню ефективну роботу. Склад груп можна змінювати, виходячи зі своїх міркувань. Далі група сильних учнів одержує окреме завдання творчого характеру, а решта учнів пишуть самостійну роботу, яка складається із завдань, аналогічних розв'язаним.      Самостійну роботу перевіряється та оцінюється. При цьому  керуюсь  особистісно-орієнтованим підходом до навчання учнів: кожний отримує посильне і водночас настільки складне завдання, щоб для його виконання прикласти розумове напруження. Слабкий учень прагне до рівня середнього, середній - до рівня сильного, сильний до самовдосконалення своїх здібностей.

     Цікавими для дітей є уроки узагальнення і систематизації знань, де вони працюють у різнорівневих групах. Урок проходить у вигляді естафети.

Команди сформовані за рівнями навчальних досягнень. У кожній з них - 4 учні. Учасники команд одночасно починають усно розв'язувати приклади, записуючи на дошці тільки відповідь. Далі передають естафету іншому учаснику, який може виправити помилку товариша, а потім розв'язати своє завдання. Всі завдання поділені на блоки. З кожним наступним блоком вони ускладнюються і оцінюються більшою кількістю балів. Так із застосуванням групової навчальної роботи з'являються нові можливості для співпраці викладача й учнів.

 

Приклади проведення нестандартних уроків та фрагменти використання ігрових методів на уроках з метою підвищення інтересу учнів до вивчення математики.

I.     Нестандартний урок по темі «Логарифмічна функція. Розв’язування логарифмічних рівнянь та   нерівностей». Цей урок проведено у вигляді подорожі і мав шалений успіх серед моїх учнів. Учні із задоволенням готувалися до цієї подорожі  і були дуже активні на уроці. Єдина негативна сторона таких уроків – це підготовка, вона потребує багато часу, адже необхідно прорахувати кожен момент уроку. Але результат перевершив всі мої сподівання, а це є найвища нагорода для викладача!  

 

 

Тема програми: «Логарифмічна функція».

Тема уроку: «Логарифмічна функція. Розв’язування логарифмічних рівнянь та   нерівностей».

Тип уроку: узагальнення й систематизація знань і вмінь.

Вид уроку: комбінований.

Форма проведення уроку: урок-гра «Прадавні сім чудес світу».

 

Мета уроку: навчальна: відпрацювання вмінь та навиків учнів;

систематизувати й узагальнити властивості логарифмічної функції, застосовувати їх до розв’язування вправ, логарифмічних рівнянь та нерівностей;  

                                 виховна: виховувати культуру розумової праці, прагнення до

отримання та вдосконалення знань, умінь і навичок; пізнавальну активність, почуття відповідальності, упевненість в собі; виховувати пізнавальний інтерес до математики та історії;

                            розвиваюча: активізувати і стимулювати розумову і

пізнавальну діяльність   учнів; розвивати самостійність, логічне мислення, уміння висловлювати та відстоювати свою точку зору, уміння обґрунтовувати та викладати свої думки.

Методи та прийоми: репродуктивний, спонукально-пошуковий; евристична бесіда,  робота з індивідуальними картками та роздатковим  матеріалом.

Обладнання:  

1.        Слайди: тема уроку, мета, девіз уроку;

2.        Стенди назв команд;

3.        Презентація  «Прадавні сім чудес світу»;

4.        Стенди кулінарних висловів;

5.        Роздатковий матеріал (індивідуальні картки, таблиці);

6.        Модель квітки з пелюстками-завданнями;

7.        Стенд домашнього завдання;

8.        Жетони для оцінювання навчальних досягнень учнів.

 

Міжпредметні зв’язки: геометрія, історія, кулінарія.

Хід уроку.

1.     Організаційний  момент (рапорт, привітання, перевірка наявності ручок та  зошитів).

Оголошую тему, мету уроку  та звертаю увагу учнів на девіз уроку.                        

                                                

                                                         Девіз уроку:

-           Що є найбільшим  у світі?

-           Простір.

-           Що є найсильнішим?

-           Розум.

-           Що є найприємнішим?

-           Досягти бажаного.

 

2.     Група заздалегідь була поділена на чотири команди, кожна команда обрала собі капітана. Урок-подорож відбувається по заданому маршруту з 7 зупинок.

3.     Подорож.

Наша  мандрівка до семи чудес світу – не лише в далекі країни, а й у далеке минуле. Ми з вами побуваємо в Далекому Єгипті, Вавилоні, Месопотамії та Давній Греції. 

У ІІ ст. до н. е. грек Філон Візантійський склав опис семи найчудовіших людських створінь. До семи чудес світу – зараховуються творіння людського генія, які своєю технічною чи художньою довершеністю викликали подив античного світу.

 

І зупинка.

Олександрійський (Фароський) маяк Нашу подорож розпочнемо з Олександрії .

Розповідь про диво світу, яке розташоване в Олександрії, нам підготувала 1 команда.

                                      (даю слово 1 команді)

Чия статуя була на вершині будівлі, ви дізнаєтесь після того, як виконаєте завдання  №1.

 

СУТЬ ЗАВДАННЯ: Кожна пелюстка ромашки з  питаннями (на магнітній дошці прикріплена ромашка з запитаннями по темі), закриває собою номер, під яким повинна знаходитись буква із зашифрованого слова та номер її розташування. Групам роздані картки (додаток 1б) куди необхідно вписувати відповідні букви. По 2 питання кожній команді, за правильну відповідь 1 бал, якщо відповіді немає або дана неправильна відповідь, то право на додаткове питання отримує наступна в черзі команда.

 (зашифроване слово – ПОСЕЙДОН).

Питання конкурсу (питання записані на аркушах у вигляді пелюсток ромашки) :

1.     Область визначення логарифмічної функції;

(множина всіх додатних чисел)

2.     Область значень логарифмічної функції;

(множина всіх дійсних чисел)

3.     Якщо a>1, то логарифмічна функція на всій області визначення ….

(зростає)

4.     Графіки яких функцій зображено на малюнку (додаток 1в)?

(логарифмічна та показникові)

5.     Назвіть точки перетину графіка логарифмічної функції з віссю оу?

(не перетинає)

6.     Якщо о<a<1, то логарифмічна функція на всій області визначення ….

(спадає)

7.     Назвіть точки перетину графіка логарифмічної функції з віссю ох?

( (1;0) )

8.     Назвіть екстремуми логарифмічної функції.

(немає)

Підводимо підсумки конкурсу.

ІІ зупинка.

Мавзолей в Галікарнасі

І знову в дорогу. Далі ми прямуємо до Галікарнасу, яке розташовувалося на території сучасної Туреччини. 

Розповідь про диво світу, яке розташоване в Галікарнасі, нам підготувала  команда №2.

                                      (даю слово 2 команді)

Щоб нам з вами піднятися на вершину цієї споруди, потрібно    виконати завдання №2, що полягає в тому, щоб встановити відповідність. Якщо правильно виконаєте завдання, то в правій частині таблиці отримаєте  ім’я дружини царя Мавсола. 

 

СУТЬ ЗАВДАННЯ: кожна команда отримує картку з завданнями (додаток 2), треба  відновити таблицю і таким чином в правій колонці, при правильних відповідях, отримаємо потрібне ім’я.  (Дружину царя Мавсола звали Артемісія.). Якщо команда отримала потрібне слово, то отримує 6 балів.

 

Підводимо підсумки конкурсу.

 

ІІІ зупинка.

Єгипетські піраміди

Далі маршрут веде нас до Давнього Єгипту, де знаходиться найдавніше і єдине з «Семи чудес світу», що збереглося до наших днів – єгипетські піраміди. Розповідь про диво світу, яке розташоване в Єгипті, нам підготувала  команда №3.

                                      (даю слово 3 команді)

 

Ця піраміда – це гробниця фараона. Для того, щоб дізнатися його ім’я необхідно виконати завдання №3.

СУТЬ ЗАВДАННЯ:  кожен учень  отримує індивідуальне завдання (додаток3а), вам необхідно розв’язати рівняння. Отримавши відповідь вам треба знайти ваш результат серед запропонованих варіантів і  записати відповідну букву( додаток 3б)  під номером, який відповідає номеру вашій картки. За кожну правильну відповідь – 1 бал, за правильне слово ( хеопс!) – ще додаткові 2 бали.

 

Найбільшою з пірамід є піраміда ХЕОПСА – одного із царів Стародавнього

Єгипту. Біля неї побудовано ще дві піраміди, для сина Хефрена та онука

Мікерина, а також менші за розмірами піраміди для їхніх цариць. 

 

Підводимо підсумки конкурсу.

 

ІV зупинка.

Висячі сади Вавилона

Далі ми мандруємо через Середземне море, де між річками Тигр та Євфрат розташоване четверте диво – Висячі сади Семіраміди.

Розповідь про четверте диво світу нам підготувала  команда №4.

                                      (даю слово 4 команді)

Ці сади ми побачимо після того, як ви виконаєте завдання №4.

 

СУТЬ ЗАВДАННЯ:  кожна команда отримує картку з завданням (додаток 4а), треба  відновити хід розв’язку нерівностей, розкласти відповідні картки по порядку  (додаток 4б) та склеїти  скетчем загальну картку. За правильну відповідь 6 балів.

(показую зображення «Висячих садів Семіраміди»)

Існує легенда, що цар Навуходоносор ІІ  наказав збудувати сади, аби догодити своїй дружині – мідійській царівні Семіраміді. Тому вони і названі її іменем. На жаль, від цієї споруди не залишилося жодних слідів.

Підводимо підсумки конкурсу (завдання вірно виконано, якщо на зворотній стороні картки отримали вислів про кулінарію).

 

4. Підведення підсумків уроку  (команду – переможця визначають за кількістю отриманих жетонів).  Оцінювання учнів.

Ось і закінчилася наша подорож країнами Старого Світу. Ми милувалися творіннями людського генія, які дивували і зачаровували подив всіх часів та народів. Вислів «Сім чудес світу» залишився, а чудес побільшало. Новітні дива творить сучасна інженерна думка та техніка. Але у великому списку чудес, якими багата наша планета, цих сім назавжди залишаться першими.

 

Закінчилась подорож, Закінчилась гра. 

І закінчувати урок 

Вже настала пора.

Сьогодні наші команди

Не витрачали час, 

Тому є кандидати

Для нагород у нас.

(підбиття підсумків, нагородження переможців).

 

5.Домашнє завдання: (зображене на слайді) 

 

1.     Підготуватися до контрольної роботи;

2.     Підготувати коротку історичну розповідь про храм Артеміди, Колос Родоський та статую Зевса для проведення другої частини уроку

 

II.     Урок-гра «Щасливий випадок»  за темою «Показникова функція».

Етапи гри:

I.                   Розминка.

II.                Переслідування лідера.

III.            Поспішайте побачити.

IV.             Темна конячка. V.   Далі, далі…

Хід гри.

Перед початком кожного етапу-гейму звучить мелодія. I.Розминка.

Кожна команда отримує напівжартівливий кросворд «Всерйоз і жартома». Та команда, яка за 1 хвилину відгадає більше слів, заробляє 1 бал.

II.            Переслідування лідера.

З бочечки капітани команд по черзі (4рази) дістають картку з номером запитання. За кожну правильну відповідь – 1 бал. За відповідь, дану

 

 

 

(Додаток 1)

 

 

 

  

III.         Наведу приклад ігрового завдання, яке займає незначну частину уроку,

але сприяє підвищенню якості знань учнів та підвищує інтерес до предмету.

Такого роду ігри можна проводити на уроках закріплення теми, наприклад: 

похідна, первісна, інтеграл або розв’язування тригонометричних, ірраціональних рівнянь…

   «Знайди помилку». Для участі в цьому завданні-естафеті обирають дві команди. Кожен учасник виходить до дошки і знаходить один неправильно розв’язаний приклад, повертається до своєї команди, передає крейду наступному гравцеві, і так далі, доки всі учасники «не пройдуть свій шлях» у завданнях, написаних на дошці або стендах, - прикладів повинно бути стільки, скільки учасників естафети. Максимальна кількість балів, присуджених за естафету, дорівнює кількості прикладів і 1 бал за швидкість розв’язування; цей бал заробляє та команда, яка найшвидше знайшла неправильні відповіді. Якщо виправлено правильний приклад, бал знімається.

 

                 IV.     Тема програми:  «Перпендикулярність прямих та площин у   

просторі».

Тема уроку: «Перпендикуляр і похила».

    Вивчення поняття перпендикуляра, похилої, проекції похилої, теореми про три перпендикуляри та її застосування посідає центральне місце в курсі геометрії  І курсу і є базою для подальшого засвоєння програмового матеріалу на ІІ і ІІІ курсах.

    Гра  “Хто швидше?”

   Метою цієї гри є перевірка, систематизація знань учнів щойно вивченого матеріалу. Я ставлю запитання , а учні відповідають. Перемагає той, хто дав більше правильних відповідей. У визначені переможця мені допомагає- учень – експерт.

1.     Що таке препендикуляр, проведений з даної точки до площини; основа перепендикуляра?

2.     Що таке похила, проведена з даної точки до площини?

3.     Що таке проекція похилої?

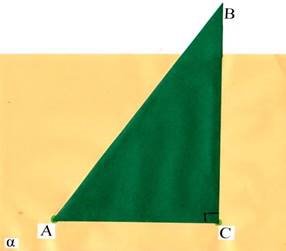
4.     Назвіть на малюнку  (Додаток 2)

а) перпендикуляр;                                             б) основу перпендикуляра;

в) похилу;                                                           г) проекцію похилої.

5.     Сформулюйте властивості перпендикуляра і похилих.

6.     Скільки перпендикулярів можна опустити з даної точки до даної площини?

7.     Скільки похилих можна побудувати з даної точки до даної площини?

Бесіда.

1)    Як ви думаєте, до чого зводиться розв’язування задач на тему

“Перпендикуляр і похила?” (До розв’язання прямокутного трикутника).

2)    Що таке відстань між будь-якими двома геометричними фігурами?

(Найменша відстань між точками фігур).

3)    З точки М до площини проведено рівні прямі МА, МВ, МС, МD. Чи може чотирикутник АВСD бути: 

а) квадратом;                             б) паралелограмом;             

 в) прямокутником;  Поясніть відповідь.

4)    Якщо в задачі йдеться про дві похилі, що їх проведено з однієї точки до площини, то розглядатимемо (продовжте речення)… .

5)    Якщо скласти по висоті, опущеній  на основу рівносторонній, рівнобедрений, різносторонній трикутники, то ці моделі, що виражатимуть?

(Твердження учнів демонструються на різнокольорових трикутниках –

Додаток 2).

      

                                    

Колективне розв’язування типових задач

1.     За даними, наведеними на малюнках знайдіть невідомий відрізок Х.

2.     Знайти проекцію похилої на площину, якщо похила дорівнюєх 13см, а перпендикуляр, проведений з тієї ж точки, - 12см. 

                Конкурс на кращий малюнок до задачі.

3.     З точки до площини проведено дві похилі. Знайдіть відстань від даної точки до площини, якщо різниця довжини похилих дорівнює 5см, а їхні проекції дорівнюють 7 і 18 см.

               Створення моделі до задачі за допомогою стереометричного ящика.

 

 

 

V. Групову  форму роботи  я намагаюся застосовувати  на уроках різних типів і відбувається таким чином:

 

Алгебра, І курс

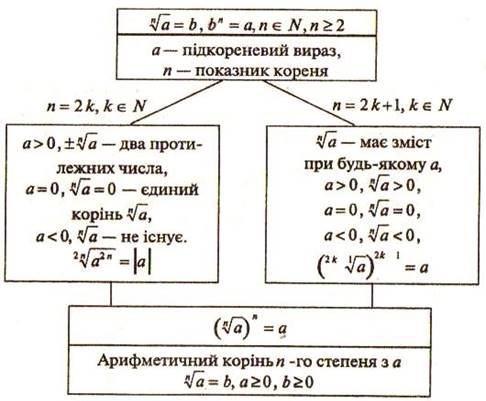
Тема уроку:  «Корінь п-го степеня. Дії над коренями».

  На початку уроку учні повторюють відомості про квадратний корінь (технологія «Асоціативний кущ») (додаток 3).

Пропоную учням указати слова (словосполучення) , які асоціюються зі словами «квадратний корінь з числа а», а далі більш детально повторюються всі  відомості, згадані учнями.

 Оголошую тему і мету уроку, пропоную учням, об’єднавшись у групи, вивчити самостійно означення кореня п-го степеня та властивості.

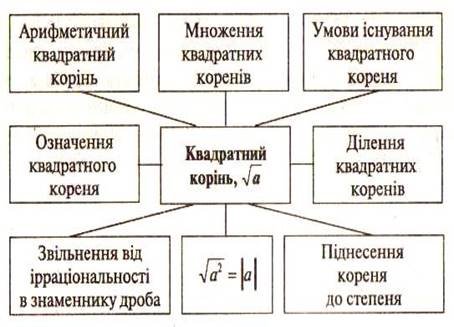
 І група (парти 1,3,5) одержує завдання: скласти «юридичну шпаргалку» (коротку наочну таблицю-схему), в якій відобразити всі відомості про корінь п –го степеня з числа а,  умови його існування, арифметичний корінь п-го степеня та властивості коренів. Учні працюють самостійно з підручником.

 ІІ група (парти 2,4,6) працюють з текстом підручника в тому обсязі, однак завдання у них таке: скласти запитання до означення та властивостей кореня п-го степеня, тобто створити так званий «опитувальник».

 Через певний час учні І і ІІ груп об’єднуються в новостворені групи і демонструють один одному свої схеми та «опитувальники», разом знаходячи відповіді на всі запитання.

       Далі пропоную представникам груп відповісти на запитання з теми біля дошки.

 Прикладом «юридичної шпаргалки» є  схема, створена учнями з моєю допомогою (додаток 4). 

На етапі рефлексії  разом з учнями ще раз наголошую на  нові частини вивченого матеріалу. Учні дають відповіді на  питання та наводять приклади.

Що нового ви дізнались на уроці?

Що називається коренем п -го степеня з числа а?

Який знак має корінь непарного степеня з додатного числа? З від'ємного числа?

За якої умови існує корінь парного степеня з числа?

Що називається арифметичним коренем п -го степеня з числа?

 

 

                    VI.   Уроки закріплення та застосування знань, умінь і навичок

На таких уроках працюють 5-6 груп  (залежно її кількості учнів групи) під керівництвом учня-консультанта (можна проводити тільки в більш сильних групах). Це учень з  середнім або високим рівнем навчальних досягнень з предмета, здатний до самостійної творчої праці, має організаторські здібності. До уроку консультанти готуються заздалегідь, одержавши від мене додаткове завдання та продемонструвавши вміння виконувати його на достатньому рівні. Я повинна бути впевнена у знаннях та вміннях консультанта.

Після етапу актуалізації знань, консультанти працюють індивідуально і розв'язують завдання достатнього рівня складності, решта учнів           розв'язують задачі усно або письмово на дошці або коментують їх з місця під моїм керівництвом.

Далі учні об'єднується в групи, і консультанти, які розв'язали свої            завдання, здають зошити  на перевірку і працюють на чолі груп з розв’язування задач з теми для закріплення знань, умінь, навичок. В цей час маю змогу перевірити виконання завдань сильними учнями, після чого можу контролювати і проконсультувати роботу в групах.  

   На  етапі рефлексії  вибірково перевіряю зошити учнів або збираю їх від 

всіх учнів групи  після уроку.

 

Геометрія, І курс.

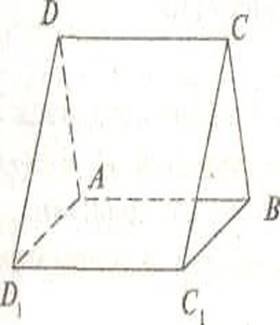
Урок закріплення та застосування знань,  умінь, навичок з теми «Взаємне розміщення прямих і площин у просторі».

Після актуалізації знань учнів (написання графічного диктанту) усі учні розділяються на дві групи: перша — учні-консультанти працюють  ідивідуально та розв'язують два типи задач: 

1.    Точки А,В,С,В D не лежать у площині КLMN  паралелограма точка К

— середина АВ, точка L — середина ВС, М — середина СD. Чи є точка N  серединою відрізка АD? (додаток 5).  

2.    Через кожну пару протилежних бічних ребер куба проведено площини. Довести, що ребро DD₁ паралельно площині: 

а) АА₁СС₁;

б) АВВ₁;

в)ВСС₁;

г) площині, що проходить через середини ребер  А ₁В₁ , АВ,ВС. Друга група учнів — розв'язують разом з викладачем задачі за готовими рисунками (усно з місця ). 

1.        АВСВ — прямокутник, АВС_І D — ромб, які лежать у різних площинах. Довести, що СС_І DD₁, — паралелограм. 

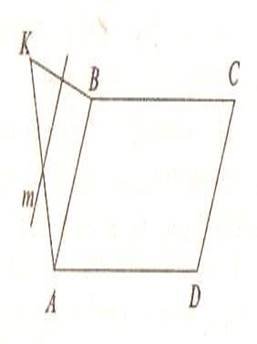
2.        Точка К не належить площині паралелограма АВСВ. Через середини відрізів АК і ВК проведено пряму т. Довести: т II СD

(додаток 5).                                             

3.        ABСD — трапеція, АВ є α. Яке взаємне розміщення ВС і α.? 

4.        Ппощина β паралельна гіпотенузі АВ прямокутного трикутника АВС.

Катети дорівнюють відповідно 3 і 4 см. (додаток 7).

Площина   перетинає АС у  точці М – середині АС, ВС – у точці N.       

 Знайти MN.

    Учні, які працювали з картками, здають свої розв'язання для перевірки  і стають консультантами для груп учнів. У групах розв'язують задачі, схожі на ті, що виконували консультанти.

         Після обговорення і складання плану розв'язування задачі консультанти готують на дошці рисунки до задач, а групу представляє будь-який  учень, крім, консультанта. Він пояснює спосіб розв'язання задачі біля дошки, а всі інші записують у зошитах план її розв’язання.

          

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток 2.3.1 І зупинка.

Олександрійський (Фароський) маяк

 

 

 

 

 

 

Додаток  1б

 

 

 

 

 

 

 

 

 

 

 

Додаток  1в

 

                    

 

 

 

 

 

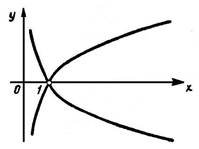
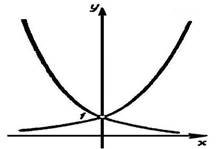
ІІ зупинка.   Мавзолей в Галікарнасі

	Завдання команді № 1	Відповіді
1.	logaxy
2.	logb N
3.	loga a
4.	aloga N 
5.	loga xloga y
6.	logablogac,   то
7.	loga1
8.	log a k N 
9.	loga xp 

 

	log x             a loga y	А
	loga N  loga b	Р
	1	Т
	N	Е
	x loga                    y	М
	bc	І
	0	С
	1 log N  k        a	І
	plog x              a	Я

ІІІ зупинка.

Єгипетські піраміди

 

Додаток  3б

 

 

 

 

Додаток  3а

 

1.                                            log₂5x0

                    Варіанти відповідей:

                     А) 8;

         Д) 42;          Х) 4;           О) 2.

 

 

 

2.                                            log_à xlog_a3log_a5

                    Варіанти відповідей:

                    А) 10;

                    Е) 15;

         Х) 25;          О) 13.

 

 

 

 

3.                                            log₃² xlog₃ x2  0

                    Варіанти відповідей:

                    А) 1; ;

                     Е) 10; ;

                    Х) 14; 7;

                     О) 9;  .

 

4.                                            log5x73

                    Варіанти відповідей:

                     В) 1;

                     П) 3 ;

                     Х) 4;

                     О)   .

 

 

 

5.                                            lgx1lg5x3

                    Варіанти відповідей:

                     А) 2 ;

                    О) 10; 

                     Х)  ; 

                   С) розв’язків немає.

 

 

 

6.                                            log₅ xlog₅x7log₅22log₅3

                    Варіанти відповідей:

                     …) 10; -3;

         ?) -2; 9;       !) 2;

                    *) -9; 2.

  

 

ІVзупинка.

Висячі сади Вавилона

 

Додаток  4а

 

Вислови:

 

1.   «Професія кухаря потрібна людині постійно»

2.   «Справжній кухар – вартий лікаря»

3.   «Кулінарія – це справжнє мистецтво!»

4.   «Праця кухаря важка, кропітка, але дуже цікава»

 

Нерівності:

 

 

1. log₃x283 a 3,

  a1        

x283³



_x280

x2827



_x28 x1   _x28



                    Відповідь:    x1

 

 

2. logx21

a,

0a1       

x 2 11 

    6 ^x 2  0

x26 _x2 x4 _x2

                              

                           

Відповідь:   x4

3. log1283x 2 log1282x3 a128,

               a1       

3x 2  2x3 3x 2  0      ^^2x3  0 3x 2x 32 3x2    ^^2x3 x1 ^x2 





 3 x11 

                          2

Відповідь:   x1

 

 

4. log2x9 log5x3

a,

                0a1       

2x9  5x3 2x9  0 ^^5x3  0 3x6



^^xx43,5

      5 x2       3



_x5

Відповідь:   x2

 

 

 

Додаток  4б

 

 

 

 

1	2	3
4	5	6

 

          

 

2.3.2

 

 

  

2.3.3

 

 

 

 

 

 

2.3.4

 

 

 

 

 

Додаток 2.3.5

 

 

 

 

 

 

2.3.6

  

                    

  

 

 

 

 

 

 

 

             

 

 

 

 

Висновок

 

                            Хочеш зробити світ кращим –

 почни зі своїх уроків!          Викладач  навчає дітей і сам вчиться протягом життя, йому треба бути завжди у вирі освітніх подій. К. Ушинський вважав, що «Учитель живе доти, доки вчиться. Щойно він перестає вчитися, в ньому помирає учитель».

   Викладач відбувся тоді, коли він хоче йти на роботу і, незважаючи на

альтернативу, не змінює професію, коли він бачить у дітях, яких навчає і виховує, результат. Кожен викладач має нести відповідальність за те, якими учні вийшли з його уроку. Тобто після уроку в учнів не повинна згаснути жага до знань і любов до життя. На уроці учень має здобувати знання і вчитися ними оперувати, витрачаючи на це лише частку своїх сил. Якщо учень протягом уроку працював - вчився встановлювати взаємозв'язки між явищами та предметами, пояснювати, аргументовано відтворювати засвоєне, публічно захищати свою думку, гідно відповідати опоненту, і при цьому не втрачати віру в себе, то урок не пройшов для неї даремно.    В сучасних умовах важливість нестандартного уроку полягає в тому, що він підвищує ефективність навчання, зацікавлює учнів до вивчення нового матеріалу. Сьогодні відбуваються дискусії щодо визначення сутності нестандартних уроків та цінності такої форми занять у навчанні. 

Отже, в умовах зміни педагогічної парадигми нестандартний урок як своєрідне педагогічне явище бурхливо розвивається, постійно набуваючи нових рис. Він – дитя перебудови суспільства і освіти, і доля його пов’язана з долею цього процесу. 

    У даній розробці я намагалась розглянути сутність поняття ролі гри та нестандартних уроків у підвищенні інтересу  учнів до вивчення математики, підготовку викладача до нестандартного уроку, значення нестандартних уроків у формуванні особистості учнів. 

    Використання нестандартних уроків математики створює сприятливі умови для: організації колективної роботи різних вікових груп, що вчаться, і груп; розширення кругозору учнів за рахунок залучення їх до вивчення додаткового матеріалу з різноманітних джерел.

    Доцільність використання  роботи підтверджена результатами. Це, перш за все,  підвищення якості знань учнів, а по-друге, підвищення інтересу учнів до  вивчення математики, зміцнення кожного учня як  повноправної особистості, здатної до самореалізації. Зрозуміло, що така форма роботи має і свої недоліки. Не завжди можу на 100% проконтролювати роботу всіх учнів, іноді виникають проблеми щодо адекватного оцінювання групою та мною  роботи. Однак вдале поєднання пасивної, активної і інтерактивної форм роботи учнів на уроках математики дають свої результати, а недоліки кожної з  форм навчання стають незначними.

    Отже, я вбачаю, що гра та нестандартні уроки дають  можливість зробити процес навчання цікавим та всепоглинаючим; створити у дітей робочий настрій; допомогти подолати труднощі в засвоєнні навчального матеріалу. 

 

 

 

 

           

 

 

 

 

 

 

 

 

 

 

Список використаних джерел 

 

1.     Возняк Г. М. Диференційовані навчальні самостійні роботи з математики, — 2000. 

2.     Воліна В. В. Світ математики. — 2005. 

3.     Коваленко В. Г. Дидактичні ігри на уроках математики. — 2011. 

4.     Онищук В.А. “Урок в современной школе”.- 2011. 

5.     Паламарчук В.Ф., Рум’янцева Д.І., Антипова О.Й. “У пошуках нестандартного уроку”. - 2010. 

6.     Пєхота О. М., Любарська О. М. та ін. Освітні технології. — 2004. 

7.     Пометун О. І., Пироженко Л. В. Сучасний урок. — 2004. 

8.     Прилуцька П. Дидактична гра на уроці // Математика в школі. — 2000. № 6. 

9.     П ехота О. М., Л ю барська О. М. та ін. О світні технології. — 2004. 

10. Підласий 1.П. “Як підготувати ефективний урок” .- 2010. 

11. П ометун О. 1., П ирож енко Л. В. Сучасний урок. — 2004.

12. Упор.Гладій Л.К. М етод проектів на уроках математики. — 2012.