Методична розробка «Самостійні роботи з алгебри, 7 клас (нова програма)»
Матеріали посібника призначені для вчителів загальноосвітніх на¬вчальних закладів, які викладають алгебру в 7 класі.
Посібник містить розробки самостійних робіт, що розраховані на 10-15 хвилин уроку та коротке пояснення теми, що відповідають новій програмі та призначається на допомогу вчителю математики.
Сарненська загальноосвітня школа
І-ІІ ступенів №3
Методична розробка
«Самостійні роботи
з алгебри,
7 клас (нова програма)»
Номінація «Математика»
Лобасюк Анна Сергіївна
Вчитель математики в
Сарненській ЗОШ І-ІІст. №3
Сарни – 2018
Автор Лобасюк А.С. Методичний посібник «Самостійні роботи з алгебри, 7 клас (нова програма)»- Сарни, 2018 - 30с.
Рецензент: Магрело Віта Володимирівна – заступник директора з навчальної роботи
Матеріали посібника призначені для вчителів загальноосвітніх навчальних закладів, які викладають алгебру в 7 класі.
Посібник містить розробки самостійних робіт, що розраховані на 10-15 хвилин уроку та коротке пояснення теми, що відповідають новій програмі та призначається на допомогу вчителю математики.
Схвалений методичною радою Сарненської загальноосвітньої школи І-ІІ ступенів №3
протокол № 2 від 04.01.2018
Передмова
Я – вчитель, і своєю професією дуже пишаюся. Особливість цієї професії полягає в тому, щоб щодня і щогодини донести учням знання. Ми – вчителі, і тому повинні відчувати, що наша робота це не лише знання, майстерність, відповідальність необхідні людям, це вміння донести ці знання до тих, кому завтра вступати в самостійне життя. Саме з усвідомлення цього й починається виконання кожним з нас свого професійного учительського обов’язку.
Предметів багата, але чому саме математика?
Математика - це найточніша наука, здатна збагатити людство новими знаннями Математика - цариця точних наук. Точні науки - це науки логіки, фактів і здорового глузду. Я люблю математику за те, що вона дисциплінує і виховує розум. Можна випадково виграти в лотерею, але неможливо стати випадково володарем розуму. А без розуму легко звести нанівець будь-яку справу.
Нерідко я чула думку: я на математичний факультет йти не збираюся, навіщо мені математика? А я вступила до факультету математики і жодного разу не пошкодувала!
Саме любов до своєї професії, до математики спонукала мене скласти цей посібник. Метою є можливість забезпечення швидкої, достовірної перевірки знань. Що є стимулом для учнів, демонстрації рівня знань і вмінь, спрямованих на відпрацювання основних навичок.
Посібник містить самостійні роботи розраховані на 10-15 хвилин уроку та коротке пояснення матеріалу, котрі відповідають новій програмі затвердженій наказом №804 від 07.06.2017року «Про оновлені навчальні програми для учнів 5-9 класів загальноосвітніх навчальних закладів».
Рекомендовано учителям математики загальноосвітніх навчальних закладів, що вивчають алгебру в 7 класах
Зміст
- Числові вирази. Вирази зі змінними……7 ст.
- Лінійні рівняння з однією змінною……..9 ст.
- Розв’язування задач за допомогою рівнянь……………………………….…..11 ст.
- Тотожно рівні вирази. Тотожність……..12 ст
- Степінь з натуральним показником. Властивості степеня………………….....13 ст.
- Додавання і віднімання многочленів…15 ст.
- Множення одночлена на многочлен…..16 ст.
- Розкладання многочленів на множники. Винесення спільного множника за дужки…………………………………….17 ст.
- Розкладання многочлена на множники. Спосіб групування……………………...19 ст.
- Добуток різниці та суми двох виразів. Різниця квадратів двох виразів. Квадрат суми та квадрат різниці двох виразів………………………………… ..20 ст.
- Сума й різниця двох кубів. Використання різних способів розкладання многочлена на множники……………………………….22 ст.
- Функція. Способи задання функції. Графік функції. Лінійна функція………………23ст.
- Лінійне рівняння з однією змінною. Розв’язування задач за допомогою рівнянь…………………………………..25 ст.
- Рівняння з двома змінними. Системи рівнянь з двома змінними. Графічний спосіб……………………………………26 ст.
- Розв’язування системи двох лінійних рівнянь способом додавання та підстановки……………………………...27 ст.
- Список використаних джерел……….....29 ст.
Числові вирази. Вирази зі змінними

Самостійна робота
Варіант 1
- Заповніть таблицю
|
у |
-4 |
-2 |
-1 |
0 |
1 |
2 |
4 |
|
5у+3 |
|
|
|
|
|
|
|
- Скласти числовий вираз і знайти його значення:
- Добуток суми та різниці чисел 1,5 та 0,1
- Різниця добутку чисел – 27 та – 10,та числа 30
- Квадрат суми чисел 305 та -1,5
- Використовуючи цифру 3 , складіть вираз, значення якого дорівнює:
- 9
- 27
- 81
- За умовою задачі складіть вираз зі змінними: Оленка купила к червоних аркушів по 1,2 грн кожний та 10 олівців по п грн. на скільки більше Оленка заплатила за олівці ніж за червоний папір, якщо к=10, п=8.
Варіант 2
- Заповніть таблицю
|
х |
2 |
6 |
-5 |
0 |
-1 |
-2 |
3 |
|
5+3х |
|
|
|
|
|
|
|
- Скласти числовий вираз і знайти його значення:
- Півсума чисел -3 та 10
- Подвоєний добуток 5 та 2
- Добуток чисел -2,5 та - 4
- Використовуючи цифру 2 , складіть вираз, значення якого дорівнює:
- 16
- 8
- 32
- За умовою задачі складіть вираз зі змінними:
Петрусь купив м кг картоплі по 3,5 грн за кілограм та 4кг моркви по в грн за кілограм. Скільки Петрик заплатив за овочі в магазині, якщо м= 5,в=2,5
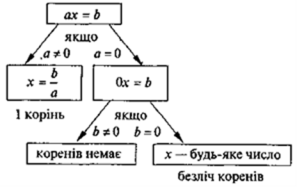
Лінійні рівняння з однією змінною
Лінійне рівняння — рівняння, обидві частини якого визначаються лінійними функціями. Найпростіший випадок має вигляд
Числа а і b є коефіцієнтами лінійного рівняння: а — коефіцієнт при змінній, b — вільний член.
Отримали назву лінійних через те, що визначають лінію на площині або в просторі.

Самостійна робота
Варіант 1
- Розв’яжіть рівняння
-
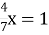
-
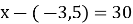
- 0,7х=-4,2
- Розв’яжіть рівняння
- |х|=3
- |х|+2=8
- При якому значенні а рівняння |х|=а має єдиний корінь?
- Які розв’язки має рівняння 4-х=2(х-3)?
-
Розв’яжіть рівняння
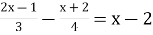
Варіант 2
- Розв’яжіть рівняння
- 3,6+х=-4,2
- 18х=9
-
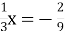
- Розв’яжіть рівняння
- |3х+2|-4=0
- 2|х|-4=0
- При якому значенні а рівняння |х|=а-2 має єдиний корінь?
- Які розв’язки має рівняння 3х-7=5х+8?
-
Розв’яжіть рівняння
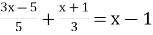
Розв’язування задач за допомогою рівнянь
Алгоритм розв’язування задач
- Невідоме позначаємо буквою.
- Використовуючи умову задачі, складаємо рівняння.
- Розв'язуємо рівняння.
- Пояснення (інтерпретація знайдених коренів відповідно до умови задачі)
Самостійна робота
Варіант 1
- Довжина одного куска дроту в 7 разів більша за довжину другого. Знайдіть довжину меншого куска, якщо він коротший від більшого на 288м.
- У Василька грошей у двічі більший ніж у Оленки. Коли Василько витратив 8 грн, а Оленка – 2 грн, то у них стало порівну. Скільки грошей було у Василька і у Оленки разом?
Варіант 2
- Дріт завдовжки 456 м розрізали на три частини, причому перша частина в 4 рази довша за третю, а друга – на 114 м довша за третю. Знайдіть довжину кожної частини.
- В один магазин завезли яблук у 2 рази більше, ніж у другий. Коли в першому магазині продали 90 кг, а у другому – 30 кг, то в обох магазинах стало порівну. Скільки яблук завезли в кожний магазин?
Тотожно рівні вирази. Тотожність

Самостійна робота
Варіант 1
- Які з виразів тотожно рівні?
- –х5 і (–х)5
- 4а2в2 і (2ав)2
- –а4 і (-а2)2
- 2а4 і (2а)4
- Знайдіть значення виразу 2х-3(1-у)+4у при х=2, у=3.
- Доведіть тотожність (а+4)(а+5)=а2+20
Варіант 2
- Які з виразів тотожно рівні?
- –х4 і (–х)4
- 3а2в2 і (-3ав)2
- (-3ху)2 і 9х2у2
- а3 ·а2 і а6
- Знайдіть значення виразу 5(-4х+0,6)+17,5х при х=8.
- Доведіть тотожність
(х+3)(х-3)=х+3(х-3)
Степінь з натуральним показником. Властивості степеня
Самостійна робота
Варіант 1
- Знайдіть значення виразу
- 1,5·62-23
-
(-3
 )3 ·(
)3 ·(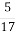 )3 –(-3)2
)3 –(-3)2
- Виконайте множення одночленів
- 0,4к3 в4 ·1,5к3 в2
-
 а5 с · (15в3 с2)
а5 с · (15в3 с2)
- Відомо, що 2т3 в = 5. Обчисліть значення виразу 4т6 в2.
- Спростить вираз
-
-1
 а3 в6 · (-
а3 в6 · (-  а2 в)3
а2 в)3
-
3
 х4 у · (
х4 у · ( х2 у3)2
х2 у3)2

Варіант 2
- Знайдіть значення виразу
- 2,5·24-72
-
(-
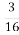 )8 ·(5
)8 ·(5 )8 – (-4)2
)8 – (-4)2
- Виконайте множення одночленів
- 0,5к7 с ·2к3 с5
-
2
 т3 п2 ·
т3 п2 · 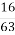 53 п4)
53 п4)
- Відомо, що 2т3 в = 5. Обчисліть значення виразу – 0,2т3 в
- Спростить вираз
-
-1
 т3 п8 · (-
т3 п8 · (- 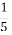 т п4)2
т п4)2
-
1
 а7 в2 · (
а7 в2 · (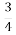 а2 в)3
а2 в)3
Многочлени. Додавання і віднімання многочленів.
Многочленом називається сума одночленів.
Самостійна робота
Варіант 1
- Запишіть многочлен у стандартному вигляді
- а – в +3а +2в2
- х + х2+х3-2х2
- Запишіть степінь многочлена відносно змінної z
- 3а z3-в z
- 0,7х z +8х2 z+5
- Обчисліть значення виразу а2 – 3а + 1, якщо
а =-1,6.
- Розв’яжіть рівняння 5-(3+4х-2х2) = 2х2-3х+8
- Замість зірочок запишіть такий многочлен, щоб утворилася тотожність:
* -(5ху-х2+2у2)=3х2+ху
Варіант 2
- Запишіть многочлен у стандартному вигляді
- 37- z3+3t-35 z3
- 7х - y2+5хy-2х · 3y
- Запишіть степінь многочлена відносно змінної z
- m3 z5-m z5
- 3 z + z3+27pz
- Обчисліть значення виразу z2 – 2z + 3, якщо
z =-2.1.
- Розв’яжіть рівняння 12+(5х+3х2) –(3х2-2х)=0
- Замість зірочок запишіть такий многочлен, щоб утворилася тотожність:
* -(5х2-4хy+у2)=7х2-3ху
Множення одночлена на многочлен.
Множення двох многочленів.
Щоб помножити многочлен на одночлен, потрібно кожний член многочлена помножити на даний одночлен і результати додати.
За цим правилом також множать одночлен на многочлен, бо множники міняються місцями.
Самостійна робота
Варіант 1
- Обчисліть значення многочлена 0,3у3+0,7у3, якщо у = 0,3.
- Розв’яжіть рівняння
-
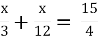 b)
b) 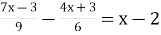
- Спростить вираз
- (х+3)(х-7) - 4х (5-2х)
- 2а (3а2+5) – (2а-7)(3а2+4)
- Купили 8 ручок двох видів, заплативши за всю покупку15 грн. скільки купили ручок кожного виду, якщо одна ручка одного виду коштує 1,5 грн, а іншого – 2,5 грн?
Варіант 2
- Обчисліть значення многочлена 1,3у2+0,3у2, якщо у = 0,02.
- Розв’яжіть рівняння
-
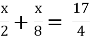 b)
b) 
- Спростить вираз
- (х-2)(х-11) - 2х (4-3х)
- 2а2 (3а+7) – (4+3а)(5а2-2)
- Продали 15 ящиків яблук та слив,загальна маса яких становить 138 кг. Скільки продали ящиків яблук і ящиків слив,якщо 1 ящик яблук важить 10 кг,а 1 ящик слив – 8 кг?
Розкладання многочленів на множники. Винесення спільного множника за дужки
Розкласти многочлен на множники – означає замінити його добутком кількох многочленів, тотожним даному многочлену. Винесення спільного множника за дужки : ах+ау має спільний множник а . На підставі розподільного закону множення
ах + ау = а (х + у). Це означає даний многочлен
ах + ау розкладено на два множники : а і х + у.
Самостійна робота
Варіант 1
- Розкладіть на множники
- ха + хв
- 2а2+3а
- 2ас2+8с3 d+4асd
- Розв’яжіть рівняння
- х (х-3) = 0
- 2х2- 2х = 0
- Доведіть, що значення виразу :
- 153-53 кратне 3
- 64-45 кратне 17
Варіант 2
- Розкладіть на множники
- 2т+2р
- 7п-14п2
- 8а4 х+7а2 х2+ах
- Розв’яжіть рівняння
- у (5-у) = 0
- 3z2- z = 0
- Доведіть, що значення виразу :
- 164-210 кратне 14
- 186-96 кратне 21
Розкладання многочлена на множники. Спосіб групування

Самостійна робота
Варіант 1
- Подайте у вигляді добутку вираз
- c(a +m) + z (a + m)
- 2 (1 - c) + c (1 - c)
- Обчисліть значення виразу 10у3 + у2 + 10у +1, якщо у = 0,3.
- Обчисліть
20,5·17 + 79,5·17+20,5·0,28+79,5·0,28
Варіант 2
- Подайте у вигляді добутку вираз
- m(n+1) + n (1+n)
- x (a +1) + 2 (a +1)
- Обчисліть значення виразу 5x3 -x2 – 5x +1, якщо x = 0,2.
- Обчисліть
42,2·42,2-42,2·41,2+57,8·57,8- 57,8·56,8
Добуток різниці та суми двох виразів. Різниця квадратів двох виразів. Квадрат суми та квадрат різниці двох виразів.

Самостійна робота
Варіант 1
- Розкладіть на множники
- p2 – x4
- x2 – 9y2
- (2a - 1)2 – 100
- Спростить вираз
- (12a - b)2 - (9a-b)(16a+2b)
- (3m – 7n)2 - 9m (m-5n)
- (7a – 5b)(7a+5b) - (4a+7b)2
- Розв’яжіть рівняння
- х2 + 8х + 16=0
- (х+3)(х-3) – х (х+4) = 0
- Розв’яжіть рівняння (2у - 3)(3у + 1) + 2 (у - 5)(у +5) = 2(1 – 2у)2 + 6у

Варіант 2
- Розкладіть на множники
- х2 – 16
- 9а2 – 4b2
- 1-(a-b)2
- Спростить вираз
- (8а - b)2 – (4a - b)(16a + 3b)
- (8k – 3n)(8k + 3n) – (6k – 5n)2
- Розв’яжіть рівняння
- 36х2 – 60х – 25 = 0
- (х + 2)(х - 2) – х (х- 6) = 0
- Розв’яжіть рівняння
4(3у + 1)2 – 27 = (4у + 9)(4у - 9) + 2(5у + 2)(2у - 7)

Сума й різниця двох кубів. Використання різних способів розкладання многочлена на множники.
Самостійна робота
Варіант 1
- Розкладіть на множники
- a3- c3
- a3 c3 + 27x3
- Подайте у вигляді многочленів
- (a - x)(a2 +ax + x2)
- (3x +y)(9x2 – 3xy + y2)
- Доведіть, що 3213 – 1233 ділиться на 198

Варіант 2
- Розкладіть на множники
- к3- c3
- a6 c6 - 27x3
- Подайте у вигляді многочленів
- (b - 2)(b2 +2b + 4)
- (2a + 3b)(4a2 – 6ab + 9b2)
- Доведіть, що 3213 + 1233 ділиться на 111
Функція. Способи задання функції. Графік функції. Лінійна функція.
Самостійна робота
Варіант 1
- Функцію задано формулою y = 0.3x. Заповніть таблицю
|
X |
-10 |
-3 |
|
|
|
|
Y |
|
|
-0.3 |
0 |
1.2 |
- Побудуйте графік функції
- y = 3x
-
y =
 x
x
- Не виконуючи побудови знайдіть точки перетину з осями координат графіка функції
у = 4х + 8
- Задайте формулою функцію, яка є прямою пропорційністю ,якщо її графік проходить через точку М(2; -9)

Варіант 2
- Функцію задано формулою y = 2x- 3. Заповніть таблицю
|
X |
-2,5 |
|
|
0,5 |
1,5 |
|
Y |
|
-6 |
-4 |
|
|
- Побудуйте графік функції
- y = 0,2x
-
y = -
 x
x
- Не виконуючи побудови знайдіть точки перетину з осями координат графіка функції
у = -х + 3
- Задайте формулою функцію, яка є прямою пропорційністю ,якщо її графік проходить через точку М(2; -7)
Лінійне рівняння з однією змінною. Розв’язування задач за допомогою рівнянь
Рівняння виду ах = в , де а і в – деякі числа, х – змінна, називається лінійним рівнянням. Числа а і в називаються коефіцієнтами даного рівняння.
Самостійна робота
Варіант 1
- Розв’яжіть рівняння 3 (2х + 5) + х = 4х -18
- Периметр прямокутника дорівнює 118 см, одна його сторона на 12 см довша від другої. Знайдіть довжини сторін прямокутника.
- Розв’язати рівняння |3х + 2| - 4 = 0
Варіант 2
- Розв’яжіть рівняння 4 (2 + х ) – х = 3х + 9
- Три трактористи зорали разом 72 га. Перший зорав на 6 га більше від другого, другий на 9 га більше від третього. Скільки гектарів зорав кожен тракторист
- Розв’язати рівняння |2х - 1| + 7 = 8
Рівняння з двома змінними. Системи рівнянь з двома змінними. Графічний спосіб.

Самостійна робота
Варіант 1
- Чи належать графіку рівняння 3х + у = 10 точки (3;1), (0; 10), (2; 4), (3; 25)
- При якому значеннні а проходить через початок координат графік 3х – 7у = 0
- Розвяжи систему рівнянь графічно
![]() 4х – у = 5
4х – у = 5
3х + 2у = 12
Варіант 2
1. Чи належать графіку рівняння 3у – 5 х = 21 точки (-4;3), (-3; 2), (1,2; 9), (-2; 5)
2. При якому значеннні а проходить через початок координат графік 5х – 2у = 0
![]() 3. Розвяжи систему рівнянь графічно
3. Розвяжи систему рівнянь графічно
х – 4у = 1
2х - 8у = 3
Розв’язування системи двох лінійних рівнянь способом додавання та підстановки.

Самостійна робота
Варіант 1
- Розв’яжіть способом підстановки
![]() 2х + 3у = 13
2х + 3у = 13
5х – у = 7
- Розв’язати способом підстановки
![]() 8х + 3у = 7
8х + 3у = 7
-4х – 5у = 7
- Розв’яжіть систему двох лінійних рівнянь
![]() 3,1х + 0,7у = 5,2
3,1х + 0,7у = 5,2
5,2х + 0,6у = 7
- Знайдіть два числа, знаючи, що їх сума дорівнює 2,5 і різниця квадратів – 2,5.
Варіант 2
- Розв’яжіть способом підстановки
![]() х + у = 2
х + у = 2
7х – 5у = -34
- Розв’язати способом підстановки
![]() 3х - 2у = 2
3х - 2у = 2
5х + 8у = 16
- Розв’яжіть систему двох лінійних рівнянь
![]() 1,5х + 0,3у = 4,5
1,5х + 0,3у = 4,5
2х – 1,7у = 6
- Два олівці і три зошити коштують 1,3 грн, а три олівці і два зошити – 1,2 грн. Скільки коштує один олівець і один зошит?
Список використаних джерел
|
Один автор |
|
|
Три автори |
|
|
Чотири автори |
|
|
Електронні ресурси |
|
1


про публікацію авторської розробки
Додати розробку
