Методичні матеріали до заняття з геометрії на тему "Паралелепіпед"

“Життя прекрасне двома речами:

можливістю вивчати математику

й можливістю викладати її”

С. Пуассон

 

Робота викладачів математики націлена формувати у студентів математичні знання, навчати їх прийомам розумової діяльності, сприяти розвитку їх пізнавальної активності, вихованню культури мислення, формуванню творчої особистості. Пошук і впровадження інноваційних технологій навчання сприяють реалізації таких цілей і завдань. ‘‘Інновація – нововведення, зміна, оновлення; новий підхід, створення якісно нового, використання відомого в інших цілях’’ – таке визначення наводить І.М Дичківська [1].

Інтерактивна форма навчання – один з прийомів інноваційних підходів до пізнавальної діяльності студентів. Існують різні варіанти визначення інтерактивного навчання. Одні вчені визначають його як діалогове навчання: “Інтерактивний – означає здатність взаємодіяти чи знаходитись в режимі бесіди, діалогу з чим-небудь (наприклад, комп’ютером) або ким-небудь (людиною). Отже, інтерактивне навчання – це перш за все діалогове навчання, в ході якого здійснюється взаємодія вчителя та учня” [2]. Найбільш розповсюдженим є визначення О.Пометун та Л.Пироженко: “Сутність інтерактивного навчання полягає в тому, що навчальний процес відбувається за умов постійної, активної взаємодії всіх учнів. Це співнавчання, взаємонавчання (колективне, групове навчання в співпраці)…”[3]. Під час інтерактивного навчання всі вчаться критично мислити та  приймати обґрунтовані  рішення, формувати навички і вміння створювати  атмосферу співробітництва, взаємодії.

Відчутним знаряддям інтерактивного навчання стали інформаційні технології. Застосування комп’ютерної техніки та інформаційних технологій на заняттях значно підвищує ефективність процесу навчання, завдяки активізації самостійної, пізнавальної, науково-дослідницької діяльності студентів.

Поєднання різноманітних традиційних і активних форм і методів навчальної діяльності сприяє зростанню якості знань, більш успішному формуванню навичок і вмінь, інтересу до навчання, виявленню можливостей і здібностей студентів.

Пропонується заняття, де використовуються різні форми і методи організації діяльності викладача і студента.

 

Тема: Прямокутний паралелепіпед

 

Мета:

• перевірити рівень засвоєння студентами знань, умінь і навичок з тем “Многогранник”, “Призма”, “Паралелепіпед”;
• ознайомити з такими поняттями як прямокутний паралелепіпед, куб, лінійні виміри прямокутного паралелепіпеда; вивчити властивості прямокутного паралелепіпеда, куба;
• розвивати пізнавальну і творчу активність, просторове уявлення, логічне мислення, пам’ять; формувати у студентів вміння раціонально виконувати навчальну роботу, узагальнювати і систематизувати навчальний матеріал;
• продовжити виховувати у студентів вимогливість до себе, зібраність, почуття відповідальності.

 

ХІД УРОКУ

 

І Організаційна частина

 

Перевірка наявності студентів та їх готовності до заняття.

 

ІІ Перевірка домашнього завдання

 

Шановні студенти! Працюємо в режимі накопичення балів, які записуються в таблицю оцінювання роботи студентів на кожному етапі заняття, отже розраховую на спільну активну роботу.

 

№ п/п

Прізвищ, ім’я студента

Д/з за-дачі

Д/з презен тації

Перехресне опиту-вання

Робота в гру-пах

Розв’язування задач

Підсумок

 

• Що задавали додому?
• Які питання виникли під час розв’язування задач?

Перевіряємо правильність виконання домашньої задачі № 26 [4] за допомогою питань:

1. Скільки граней має паралелепіпед? (Шість).
2. Які властивості протилежних граней? (Рівні і лежать в паралельних площинах). Отже, маємо дві грані з площею 1м², дві грані з площею 2м² і дві грані - 3м².
3. Як шукати тоді повну поверхню паралелепіпеда? (Додати площі трьох різних граней і помножити на 2). (1+2+3)·2=12 (м²)
4. Існує інший спосіб розв’язування задачі; студент або викладач демонструє його.

 

В цей час студент біля дошки записує розв’язок домашньої задачі № 29 [4].

 

• За ці відповіді вам уже виставлені перші бали, але не зупиняємось, працюємо далі, щоб заробити більше балів.
• На наших заняттях ви працюєте не тільки індивідуально, а об’єднуєтесь в групи або команди для спільної роботи. Так, пару занять тому, перша і друга команди отримали випереджувальне завдання: створити презентації по темі “Призма” і темі “Паралелепіпед” відповідно. Бажаю успіху командам в представленні цих презентацій! (Додаток 1.), (Додаток 2.)

При інтерактивній моделі навчання наявність творчих (часто домашніх) завдань являються обов’язковими, що стимулює пізнавальну активність і самостійність студентів. Розв’язання такого завдання вимагає від них творчості, вміння колективно співпрацювати, додаткового оволодіння засобами інформаційно-комп’ютерних технологій.

Представники першої та другої команди проводять підготовлені презентації. Після перегляду цих робіт потрібно відмітити найбільш яскраві позитивні вдалі моменти слайд-презентації кожної команди.

Робимо підсумок виконання домашнього завдання. Викладач виставляє бали в таблицю оцінювання.

 

ІІІ Активізація та корекція опорних знань

 

З метою активізації знань і вмінь студентів використаємо такі інтерактивні технології:

• колективна гра “Ти мені – я тобі ”;
• робота в групах, як спосіб спільного вирішення проблеми.

- Завдяки переглянутим презентаціям ви повторили навчальний матеріал минулих занять. Це необхідно нам для подальшої роботи. Пропоную провести перехресне опитування команд у вигляді гри “Ти мені – я тобі ”. Студенти з кожної команди по черзі задають питання по темам “Многогранник”, “Призма”,  “Паралелепіпед”. Важливо, щоб студенти, які задають питання, самі знали правильну відповідь і могли її пояснити. Такий вид навчальної діяльності розвиває самодисципліну, відповідальність, зібраність, увагу.

 Робимо аналіз роботи команд.

 

- Тепер попрацюємо в групах (по 4-5 чоловік). Девізом нашої роботи буде вислів Генрі Форда: “Зібратися разом – це початок, триматися разом – це прогрес, працювати разом – це успіх”.

Кожна група отримує і виконує однакові завдання. На картках-завданнях записуються прізвище студентів, а потім представники кожної групи одночасно виходять до дошки і по черзі дають відповіді з обґрунтуваннями. Це питання:

 

1. Многогранник має 6 граней і 7 вершин. Скільки він має ребер?
2. Призма має 10 граней. Який многокутник лежить в її основі?
3. Якими фігурами є бічні грані прямого паралелепіпеда?

 

Студентам потрібно скооперуватися для успішного виконання завдань, активної співпраці, вироблення навичок спілкування, аргументації своїх позицій. Таким чином до спільної роботи залучаються всі студенти .

Робимо аналіз роботи груп. Викладач виставляє бали в таблицю оцінювання. Цей етап заняття дає можливість викладачу визначити рівень засвоєння студентами навчального матеріалу і зробити певні висновки.

 

 

ІV Мотивація навчальної діяльності

 

Висування проблемного питання:

• Чи існує паралелепіпед, усі грані якого прямокутники? Квадрати?
• Як тоді буде називатись такий паралелепіпед?

Постановка проблем посилює увагу студентів, активізує процес сприймання і усвідомлення того, що пояснює вчитель.

 

V Вивчення нового матеріалу

 

Повідомлення теми і мети заняття

«Прямокутний паралелепіпед»

Мета: ознайомити з такими поняттями як прямокутний паралелепіпед, куб, лінійні виміри прямокутного паралелепіпеда; вивчити властивості прямокутного паралелепіпеда, куба; використати отримані знання під час розв’язування задач.

 

План

1. Означення та властивості прямокутного паралелепіпеда.
2. Означення та властивості куба.
3. Властивість квадрата діагоналі прямокутного паралелепіпеда.
4. Розв’язування задач.

 

На своїх заняттях для вивчення нового матеріалу використовую такі засоби навчання як підручник, оскільки важливим завданням навчання математики є формування у студентів уміння працювати з підручником, а також моделі, рисунки, предмети оточення. Вивчення даної теми відбувається у вигляді діалогового навчання, взаємодії студентів і викладача.

Викладач формулює означення прямокутного паралелепіпеда і робить малюнок фігури на дошці. Студенти записують означення в зошит з підручника і роблять малюнок прямокутного паралелепіпеда. Викладач демонструє моделі прямокутних паралелепіпедів. Звертає увагу студентів на використання даного многогранника в навколишньому житті, зокрема в архітектурі, машино- і приладобудуванні та в інших галузях. Колективно формулюють властивості прямокутного паралелепіпеда і записують їх в зошити. Викладач формулює означення лінійних розмірів (вимірів) прямокутного паралелепіпеда; демонструє їх на моделі; студенти записують означення в зошити. 

Після демонстрації моделі куба студенти самостійно формулюють його означення і властивості; записують їх в зошити.

Далі формулюємо і доводимо теорему про квадрат діагоналі прямокутного паралелепіпеда так, як це запропоновано в [5].

Кращому усвідомленню означень і властивостей прямокутного паралелепіпеда та куба, розвитку просторових уявлень сприятимуть задачі, які розв’язуються на занятті.

 

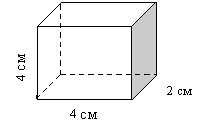Задача. Виміри прямокутного паралелепіпеда дорівнюють 4 см, 4см, 2 см. Знайдіть:

а) довжину діагоналі прямо-

кутного  паралелепіпеда;

б)довжину діагоналі наймен-

шої грані;

в) площу найбільшої грані;

г) площу поверхні

прямокутного паралелепіпеда.

 

VІ Узагальнення і систематизація знань

 

Тестовий контроль знань. Провести графічний диктант (слайди) з комп’ютерною підтримкою. Вказати, які з наведених тверджень правильні (+), а які – неправильні (-). (Додаток )

1. Паралелепіпедом називається призма, основою якою є паралелограм.
2. Паралелепіпед має чотири основи.
3. У прямому паралелепіпеді бічне ребро перпендикулярне до сторін основи.
4. Якщо в призмі дві сусідні бічні грані перпендикулярні до площини основи, то призма пряма.
5. Вимірами прямокутного паралелепіпеда називаються довжини ребер, які не мають спільної точки.
6. У прямому паралелепіпеді всі діагоналі рівні.
7. Діагональним перерізом призми є переріз призми площиною, яка проходить через два бічні ребра, що лежать на протилежних бічних гранях.
8. У прямокутному паралелепіпеді квадрат будь-якої діагоналі дорівнює сумі квадратів лінійних розмірів.

9. Виміри прямокутного паралелепіпеда дорівнюють 3 см,    2см 6 см, тоді площа найбільшої грані дорівнює 18 см².

10. Кубом називається пряма призма, у якої всі ребра рівні.
11. Якщо ребро куба дорівнює 3 см, то площа його поверхні - 36см².

 

VІІ Рефлексія. Підведення підсумків.

 

Гра “Мікрофон ”.

1. Що ми робили назанятті?
2. Чи досягли поставленої мети?
3. Чи сподобалось працювати в групах?
4. Який із видів роботи сподобався найбільше?

Аналіз активності студентів. Викладач оголошує оцінки студентів з таблиці оцінювання.

 

VІІІ Домашнє завдання

 

§ 5, п.45-46; контрольні запитання № 23-26; задачі № 35, 37, 38 (с. 79) [4].

 

Література:

 

1. Дичківська І.М. Інноваційні педагогічні технології: Навчальний посібник. – К.: Академвидав., 2004. – 352 с.
2. Дьяченко В.К. Сотрудничество в обучении: О коллективном способе учебной работы. – М.: Просвещение, 1991.
3. Пометун О., Пироженко Л. Інтерактивні технології навчання: теорія і практика. – К., 2002. – 136 с.
4. О.В.Погорєлов, Геометрія. Стереометрія. Підручник для 10-11кл., -К.,: Шк.підр., 2006- 128 ст.
5.  О.М. Роганін, Геометрія 11кл., Плани-конспекти уроків. Ранок, 2006. -256ст.
6.  Геометрія в таблицях 7-11 класи Навч. пос.- Х.: Науково-методичний цент ТМ, 2003 -168ст.
7. Бабіно В.М. Інноваційні підходи в реалізації змісту методів викладання природничих дисциплін через гуманізацію навчального процесу. / Організація навчально-виховного процесу. З досвіду роботи вищих навчальних закладів І-ІІ рівнів акредитації. – НМЦ, вип.12, 2008.