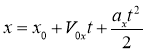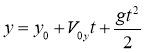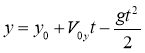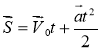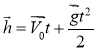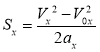Методичні матеріали "Кінематика"

Зміст

Зміст

1. Методичне обґрунтування теми…………………………….………………3

2. Структура теми……………………………………………………………….3

3. Очікувані результати………………………………………………………..4

4. Основні визначення та формули до теми «Кінематика»………...........5

5. Приклади розв’язування типових задач……………………………….18

6. Запитання для перевірки теоретичних знань з теми «Кінематика»….23

7. Якісні задачі для самостійного розв’язання.……………………………25

8. Розрахункові задачі для самостійного розв’язання:

середній рівень…………………………………………….……………27

достатній рівень………………………………………………………..28

високий рівень….………………………………………………………29

9. Додаток 1…………….……………………………………………………...30

10. Додаток 2…………………………………………………………………..31

11. Додаток 3…………………………………………………………………..31

12. Список використаних джерел………………………………………….32

 

 

 

 

 

 

Методичне обґрунтування теми

«Кінематика»

Структура теми «Кінематика» сприяє забезпеченню формування базових понять в учнів.

Під час вивчення теми учні дізнаються не лише про механічний рух, його види та основні характеристики, про прискорення та рівноприскорений рух, а також про вільне падіння тіл, як окремий випадок рівноприскореного руху, і рівномірний рух по колу, а й матимуть змогу сформувати уявлення про відносність та швидкість руху тіл. Також учні зможуть сформулювати основну задачу механіки та вмітимуть розв’язувати її, як для прямолінійного руху так і для руху тіла по колу. Учні розрізнятимуть поняття фізичне тіло і матеріальна точка. Зможуть будувати графіки руху тіла для рівномірного ті рівноприскореного руху.

 Матеріал теми дібрано таким чином, щоб учні могли перевірити дослідним шляхом те, що вивчають теоретично.

 Застосування різних форм і методів роботи на уроках стимулюватиме творчу активність учнів, формуватиме вміння будували структурно-логічні схеми матеріалу та виділяти головне серед усього різноманіття інформації.

 

 

Структура теми

Відповідно до держаного стандарту та навчальної програми для професійно-технічних навчальних закладах на вивчення теми «Кінематика» відводиться 10 годин, з яких 1 урок виділяється для лабораторної роботи «Визначення прискорення тіла при рівноприскореному русі». Під час вивчення теми учні вивчають так питання: механічний рух та його види, основна задача механіки та способи її розв’язання в кінематиці, фізичне тіло і матеріальна точка, система відліку, відносність механічного руху, траєкторія руху, рівномірний прямолінійний рух, шлях і переміщення при рівномірному прямолінійному русі, швидкість тіла і пройдений шлях, графіки руху тіла, рівноприскорений рух та прискорення, швидкість тіла і пройдений шлях, під час рівноприскореного прямолінійного руху, вільне падіння тіл та прискорення вільного падіння, рівномірний рух по колу та характеристики руху по колу.

Очікувані результати

Після вивчення теми учень зможе:

назвати окремі види рухів за їх траєкторією, одиниці вимірювання основних фізичних величин, які характеризують ці рухи;

розрізняти фізичне тіло і матеріальну точку, прямолінійний і криволінійний рух матеріальної точки;

формулювати означення кінематичного рівняння, кінематичні закони рівномірного та рівноприскореного рухів уздовж прямої;

зможе описати явище вільного падіння тіл та вид механічного руху за його кінематичним рівнянням руху;

обґрунтовувати суть методу фізичного моделювання, зміст основної задачі механіки, рівняння руху як залежність координати від часу;

характеризувати роль фізики у житті людини; рух тіла у тіла у вертикальному напрямі, зв'язок лінійних і кутових величин, що характеризують рух матеріальної точки по колу; вид механічного руху за його рівнянням швидкості та її зв'язок із частотою обертання; суть фізичних ідеалізацій – матеріальної точки, системи відліку; порівняти основні кінематичні характеристики різних видів руху за відповідними їм рівняннями рухів;

досліджувати рівноприскорений рух тіла та визначати прискорення руху тіла при рівноприскореному русі;

розв’язувати задачі застосовуючи кінематичні рівняння руху;

будувати графіки руху для рівномірного та рівноприскореного рухів.

Основні визначення та формули до теми «Кінематика».

Все наше життя з ранку й до вечора, проходить у постійному русі: вранці люди поспішають до навчального закладу чи на роботу, ввечері — додому. Їдуть в автобусі, ходять в туристичні походи, займаються спортом і постійно рухаються. Все наше життя — це рух.

Якщо деяке тіло змінює своє положення в просторі, то про нього говорять, що воно здійснює механічний рух.

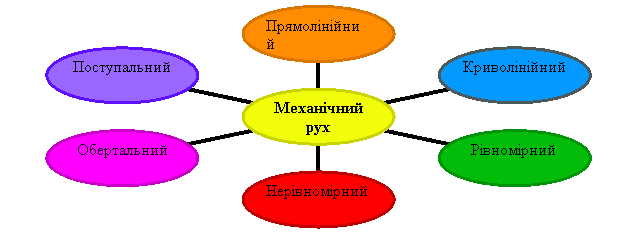
Механічним рухом називають зміну з часом положення тіла в просторі відносно інших тіл.

Вивченням механічного руху займається розділ фізики, що називається механікою.

 

Прямолінійний рух – це рух по прямолінійній траєкторії.

Криволінійний рух – це будь який рух крім прямолінійного.

Рівномірний рух – це рух, при якому тіло за рівні проміжки часу проходить однакову відстань.

Нерівномірний рух – це рух, при якому тіло за рівні проміжки часу проходить різну відстань.

Обертальний рух – це рух тіла по колу.

Поступальний рух – це рух, при якому будь-яка пряма, що пов’язана з тілом, переміщується паралельно собі.

Основна задача механіки полягає в тому, щоб визначити положення руху тіла в будь-який момент часу.

Розв'язати основну задачу механіки означає написати математичне рівняння залежності координати тіла від часу.

Для того, щоб говорити про механічний рух, у просторі має бути, принаймні, два тіла: те, за яким спостерігають, і те, відносно якого розглядається положення досліджуваного тіла.

Тіло відліку – це тіло, відносно якого розглядається рух інших тіл.

Механічний рух здійснюють фізичні тіла. Реальні фізичні тіла мають форму, розміри, об'єм, здатність до деформації тощо. Але для спрощення опису механічного руху зручно замінити реальні тіла абстрактними, які не мають даних властивостей. У кінематиці такі тіла називають матеріальними точками.

Матеріальна точка — тіло, розмірами якого можна знехтувати в умовах даної задачі.

Наприклад, якщо розглядати падіння м’яча відносно Фрекен Бок, м’яч можна вважати матеріальною точкою, а при вивченні деформації м’яча при ударі об підлогу — ні (мал. 1).

Для того, щоб записати рівняння залежності координати досліджуваного тіла від часу його руху потрібен прилад для вимірювання часу – годинник.

 Мал. 1.               Тіло відліку та пов’язана з ним система координат, матеріальна точка і годинник разом утворюють систему відліку.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

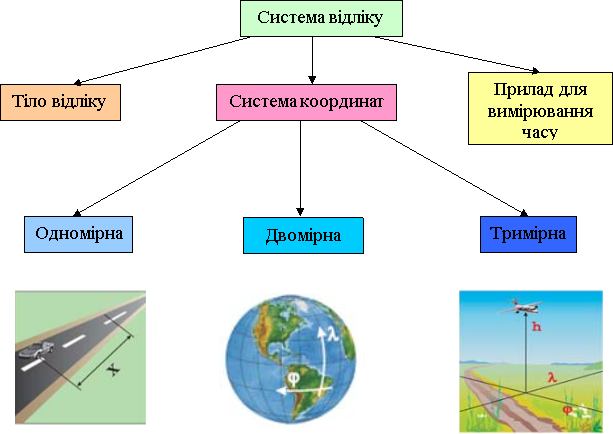
Розглядаючи політ малюка та Карлсона їх можна вважати матеріальною точкою, за тіло відліку можна прийняти дах будинку над яким вони пролітають, а    годинник доповнить систему відліку.

Оскільки ми самостійно можемо обирати тіло відліку, то один і той же рух відносно різних тіл може відбуватись по різному. В такому випадку говорять про відносність руху. Так, наприклад, під час польоту малюка та Карлсона вони рухаються відносно будинків над якими пролітають, але залишаються нерухомими відносно один одного (мал.2).                                                 Мал. 2.

Під час свого польоту малюк та Карлсон рухаються по певній траєкторії, при цьому вони переміщуються та пролітають певний шлях.

Траєкторія руху тіла – це лінія, уздовж якої рухається тіло.

Форма траєкторії може бути будь-якою: пряма лінія, дуга кола, парабола, ламана лінія. Тому за формою траєкторії рух тіл розділяють на прямолінійний та криволінійний.

Форма траєкторії залежить від вибору системи відліку, адже той самий рух у різних системах відліку може виглядати по-різному.

Довжину траєкторії називають шляхом, пройденим тілом.

Шлях позначають S. Одиницею шляху в CI є метри.

Переміщенням тіла називають спрямований відрізок, проведений з початкового положення тіла в його положення в даний момент часу.

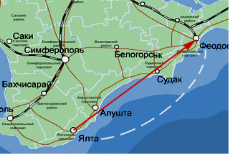Наприклад, якщо малюк та Карлсон будуть летіти із Ялти у Феодосію, то пролетівши над морем по лінії позначеній білим пунктиром вони будуть летіти по криволінійній траєкторії, а червоний вектор на мапі буде їх переміщення (мал.3).

Мал. 3.                                       Переміщення позначають символом і характеризують числовим значенням (довжиною) та напрямком.

Величини, що характеризуються числовим значенням і напрямком, називають векторними. Числове значення векторної величини називають її модулем.

«Карлсон та малюк летіли по прямолінійній траекторії зі швидкістю 3м/с.» Почувши це ми інтуїтивно розуміємо, що за кожну секунду часу вони подолали відстань 3м. А якщо вони летіли по прямолінійній траєкторії і за 10с подолали  50м і при цьому не збільшували та не зменшували свою швидкість, то це означає, що щосекунди вони пролітали 5м. Тобто швидкість їхнього руху становила 5метрів за секунду.

У цих прикладах ми вважали, що малюк та Карлсон рухалися так, що за рівні проміжки часу вони долали однакові відрізки шляху. Такий рух називають рівномірним.

Прямолінійним рівномірним рухом називають такий, рух, за якого тіло за будь-які рівні проміжки часу здійснює рівні переміщення, рухаючись по прямолінійній траєкторії.

В попередніх прикладах ми розглядали прямолінійний рівномірний рух, але ці рухи не однакові. Різниця між ними полягає в тому, що малюк та Карлсон літали з різною швидкістю.

Швидкістю прямолінійного рівномірного руху називають відношення переміщення до проміжку часу, за який відбулося це переміщення.

.

Швидкість позначають літерою V. Одиницею швидкості в СІ є м/с.

1 м/с — це швидкість такого рівномірного руху, у ході якого тіло за кожну секунду проходить шлях в 1 м.

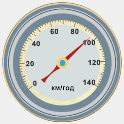Швидкість руху тіла можна виміряти двома способами: прями (за допомогою спідометра (мал.4.)) та непрямим (розрахувавши за формулою).

Якщо відомі швидкість тіла й час при рівномірному русі, то можна знайти пройдений ним шлях:

Мал. 4.        S = V*t.

Можна знайти так само й час, протягом якого рухалося тіло:

t = S/V.

Швидкість – величина відносна, і залежить від вибраної системи відліку. Якщо переміщення тієї самої матеріальної точки розглядати відносно двох систем відліку, пов’язаних з нерухомим тілом і рухомим, то можна сформулювати закон додавання швидкостей.

Закон додавання швидкостей: швидкість тіла відносно нерухомої системи відліку дорівнює векторній сумі швидкості тіла відносно рухомої системи відліку і власне рухомої системи відносно нерухомої:

,

де і - швидкості тіла відносно нерухомої і рухомої системи відліку відповідно, а - швидкість рухомої системи відліку відносно нерухомої.

Наприклад, за рухом зайця по палубі корабля з берега спостерігає вовк та капітан корабля, який і сам в той час стоїть на палубі. Отже відносно вовка заєць буде рухатись зі швидкістю яка дорівнює сумі швидкостей руху корабля відносно вовка і швидкості руху зайця відносно палуби корабля (мал. 5), а відносно капітана заєць буде рухатись тільки із власною швидкістю.                                                                                                                                    Мал. 5.

Розв’язанням основної задачі механіки для прямолінійного рівномірного руху є рівняння:                                         

x = x₀ + V_x(t).

Дане рівняння в скалярному вигляді записують так:

x = x₀ ± V(t).

Якщо тіло рухається вздовж осі Ox, то V_x = V, якщо проти, то V_x = −V.

У багатьох випадках рух тіл зручно описувати за допомогою графіків.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рівномірно й прямолінійно тіла рухаються лише на невеликих відрізках своєї траєкторії, а при переході на інші ділянки їхня швидкість змінюється. Якщо виміряти відстані, які подолали малюк та Карлсон за рівні проміжки часу, то ми побачимо, що вони будуть різними, адже спочатку вони збільшували свою швидкість, а перед приземленням – зменшували. Якщо їх швидкість змінювалась рівномірно, тобто за рівні проміжки часу на однакову величину, то такий рух називають рівноприскореним.

Рівноприскореним рух – це рух при якому тіло за однакові проміжки часу змінює свою швидкість на однакову величину.

Рівноприскорений рух це рух з прискоренням.

Прискорення – це векторна фізична величина, що дорівнює відношенню  зміни швидкості тіла до інтервалу часу, протягом якого ця зміна відбулася.

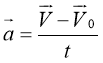
Прискорення позначають літерою α. Одиницею прискорення в СІ є м/с².

1 м/с² — це прискорення такого рівноприскореного руху тіла, при якому за 1 с швидкість тіла змінюється на 1 м/с.

 

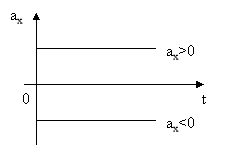
Оскільки прискорення векторна величина, то визначається воно величиною (модулем) та напрямком. В залежності від того збільшується чи зменшується швидкість тіла воно може бути додатнім чи від’ємним (рис. 1).

                              

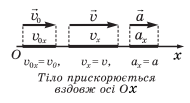
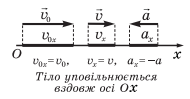
      Рис. 1.

Кінцеву швидкість тіла при рівноприскореному русі можна визнати чи за формулою:

,

де V₀ – початкова швидкість тіла, α – прискорення руху тіла, t – час протягом якого відбулась зміна швидкості.

 

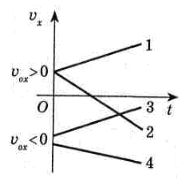
Для рівномірного руху проекція переміщення S_х чисельно дорівнює площі фігури, обмеженої графіком V_x (t) та віссю Ot. Це справджується і для нерівномірного руху, тому що час руху можна розбити на такі малі інтервали часу, протягом кожного з яких рух тіла можна вважати практично рівномірним (рис. 2).

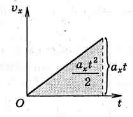
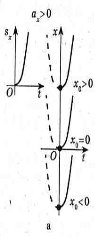
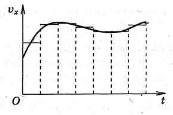Якщо початкова швидкість тіла дорівнює нулю, фігура, обмежена графіком V_x(t) і віссю Ot, - трикутник площею a_xt² / 2 (рис. 3).

         Рис. 2.      Рис. 3.

Переміщення тіла при рівноприскореному русі без початкової швидкості переміщення визначають за співвідношенням:

.

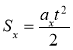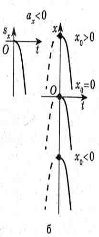
Якщо початкова швидкість тіла не дорівнює нулю, фігура, обмежена графіком V_x(t) і віссю t, - трапеція, що складається з прямокутника площею V_0xt і трикутника площею a_xt² / 2 (рис. 4).

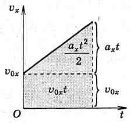           Рис. 3.

 

 

 

     

       Рис. 4.

Переміщення тіла при рівноприскореному русі з початковою швидкістю визначають за співвідношеннями:

    

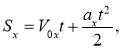
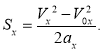
Розв’язанням основної задачі механіки для рівноприскореного руху є рівняння:

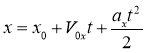
Як і рівномірний рух рівноприскорений рух також зручно описувати за допомогою графіків наведених у таблиці 1 (Додаток 1).

Рухаючись з прискоренням тіла можуть рухатися не тільки в горизонтальному напрямку але і у вертикальному.

Рівноприскорений прямолінійний рух у вертикальному напрямку подібний до вільного падіння тіла.

Вільне падіння – це падіння тіл у безповітряному просторі (вакуумі).

Вільне падіння – це падіння тіл в умовах, коли опором повітря можна знехтувати.

Вільне падіння – це рух тіла, який відбувається тільки під дією земного тяжіння без будь яких інших впливів на тіло.

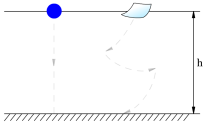
Великий учений давнини Арістотель на підставі спостережень створив теорію, згідно з якою чим важчим є тіло, тим швидше воно падає. Ця теорія проіснувала дві тисячі років – бо куля, в повітрі, дійсно падає швидше ніж аркуш паперу
(мал. 6).

                        

 

Мал. 6.

Проте у вакуумі, тобто в безповітряному середовищі, цей процес відбуватиметься інакше.

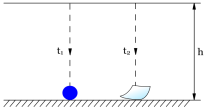
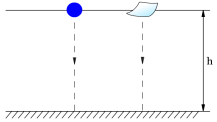Якщо у вакуумі провести той же дослід, то куля і аркуш паперу досягнуть поверхні одночасно (мал. 7).

 

 

 

 

 

 

       Мал. 7.

Якщо взяти два тіла, легке і важке, зв’язати їх до купи й кинути з висоти, то легке тіло, яке завжди падає повільніше повинно «пригальмовувати» падіння важкого тіла. Отже зв’язані тіла мають падати повільніше, ніж одне важке тіло. Водночас зв’язані тіла можна вважати одним тілом, ще більш важким, і, отже, зв’язані тіла мають падати швидше, ніж одне важке тіло!

Виявивши цю суперечність, Галілео Галілей вирішив перевірити на досліді, як же насправді падатимуть кулі різної ваги: нехай відповідь на це питання дасть сама природа. Він виготовив дві кулі та скинув їх із Пізанської вежі (Мал. 8.) – обидві кулі впали одночасно!

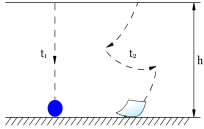
Для того щоб сфотографувати вільне падіння

Мал. 8.   кульки можна скористатись методом стробоскопічної фотографії (Мал. 9.). Кульку, що падає фотографують на фоні лінійки, освітлюючи її почергово через рівні проміжки часу, починаючи від початку руху кульки. За такою фотографією легко встановити, що за рівні проміжки часу кулька проходить різні відстані, до того ж вони пропорційно збільшуються.

Порівняння відношення переміщень і квадратів часу доводить, що вільне падіння є рівноприскореним рухом.              Мал. 9.

Прискорення вільного падіння позначають символом g.

Прискорення вільного падіння – це векторна величина, яка завжди напрямлена вертикально вниз – до центру Землі, не залежить від маси тіл, що падають.

Експериментальним шляхом встановлено, що середнє значення прискорення вільного падіння дорівнює 9,8 м/с². Але прискорення вільного падіння залежить від географічної широти місцевості, в якій воно визначається, та висоти над рівнем моря. Так на середніх широтах прискорення вільного падіння дорівнює 9,8 м/с², тоді як біля екватора
9,78 м/с², а на полюсах 9,83 м/с² ця різниця зумовлена обертанням Землі навколо власної осі. Величина прискорення вільного падіння також залежить від густини земних порід. У місцях залягання залізних руд воно більше, ніж там, де породи мають меншу густину. Це пояснюється підсиленням тяжіння в місці залягання руди. На цьому факті заснована розвідка корисних копалин.

Прискорення вільного падіння різне біля поверхні різних небесних тіл. Наприклад, для Меркурія g = 3,68 м/с², Урана - g =8,86 м/с², Юпітера -
g =23,95 м/с², Місяця - g =1,62 м/с², Сонця - g = 273,1 м/с².

 

   Земля          Меркурій              Уран                   Юпітер                 Місяць                  Сонце

  g = 9,8 м/с²       3,68 м/с²          g =8,86 м/с²             g =23,95 м/с²         g =1,62 м/с²                g = 273,1 м/с²

 

Поняття вільного падіння має широке значення: тіло здійснює вільне падіння не лише в тому випадку, коли його початкова швидкість дорівнює нулю. Якщо тіло кинуте вниз із початковою швидкістю V₀, то воно при цьому також вільно падатиме. Навіть більше, вільне падіння не обов'язково являє собою рух униз. Якщо початкова швидкість тіла спрямована вгору, то тіло під час вільного падіння певний час летітиме вгору, зменшуючи свою швидкість, і лише потім почне падати вниз.

Під час підйому тіла його швидкість зменшується відповідно до формули V = V₀ - gt. Отже, швидкість дорівнюватиме нулю через час
t_під = V₀/g. Досягши найвищої точки, тіло на мить зупиниться і почне рухатися з прискоренням вільного падіння. Швидкість тіла під час руху вниз збільшуватиметься відповідно до формули V = gt, де час t відлічується тепер від моменту, коли тіло перебуває в найвищій точці.

Оскільки вільне падіння та рух тіла кинутого вертикально в гору є рівноприскореними, то всі кінематичні рівняння справедливі і для даного випадку. Але при записі кінематичних рівнянь для кожного виду руху тіла необхідно враховувати особливості певного руху.

Рівняння за якими визначаються швидкість, координата та переміщення під час рівноприскореного руху, руху тіла кинутого в гору та під час вільного падіння тіла наведені в таблиці 2 (Додаток 2).

В природі і техніці не часто зустрічається прямолінійний рух. Частіше ми маємо справу із криволінійним рухом. Найпростіший вид криволінійного руху – рух по колу.

Рівномірний рух матеріальної точки по колу – це рух, за якого тіло за будь-які рівні проміжки часу здійснює однакові переміщення, тобто проходить дуги рівної довжини.

Наприклад, коли Карлсон літає навколо Фрекен Бок, і переміщується при цьому із точки А в точку В,                  

 він рухається по криволінійній траєкторії (мал. 10).                 Мал. 10.

При цьому пройдений шлях – це довжина дуги АВ, а модуль переміщення – це довжина хорди АВ (оскільки переміщення спрямоване вздовж цієї хорди).

Рух тіла по колу характеризують лінійною (миттєвою) швидкістю, кутовою швидкістю, періодом обертання та частотою обертання.

Лінійна (миттєва) швидкість – це швидкість, з якою тіло рухається по колу.

Лінійна швидкість позначають V. Одиницею лінійної швидкості є м/с.

1 м/с – це лінійна швидкість при якій тіло рухаючись рівномірно по колу проходить дугу завдовжки 1м за 1с.

Модуль лінійної швидкості можна визначити співвідношенням:

       ,

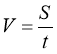де S – довжина пройденої дуги, t – час руху тіла.

Довжина дуги розраховується за формулою

,

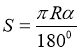де α – центральний кут дуги

Кутова швидкість рівномірного руху по колу – це швидкість, модуль якої дорівнює куту повороту радіуса, який сполучає матеріальну точку з центром кола, до часу цього повороту.

Кутова швидкість позначається символом ω. Одиницею кутової швидкості є рад/с.

1 рад/с – це кутова швидкість, за якої за кожну секунду пряма, яка сполучає матеріальну точку з центром кола (радіус), повертається на кут 1 радіан.

,

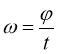де φ – кут повороту радіуса, t – час повороту.

Період обертання – це відношення часу руху до числа обертань, зроблених за цей час.

Період обертання – це час, за який тіло робить один повний оберт.

Період обертання позначається символом Т. Період – величина скалярна, в СІ вимірюється в секундах (с).

              ,

де t – час руху тіла, N – число обертів, R – радіус кола, по якому рухається тіло, V – швидкість руху тіла.

Частота обертання – це відношення числа обертань до часу за який вони здійснені.

Частота обертання позначається символом ν. Частота – величина скалярна, в СІ вимірюється в 1/с, с^-1, Гц.

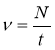
Формули, які пов’язують величини, що характеризують рух тіла по колу наведені в таблиці 3 (Додаток 3).

Ще одна з важливих характеристик рівномірного руху по колу – доцентрове прискорення.

Доцентрове прискорення – це векторна фізична величина, яка в кожній точці кола напрямлена вздовж радіуса до центра кола і чисельно дорівнює відношенню квадрата лінійної швидкості до радіуса кола.

         .

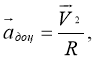
Доцентрове прискорення позначається α_доц. Доцентрове прискорення – векторна величина, в СІ вимірюється в м/с².

 

 

 

Основну задачу механіки можна розв’язати і для рівномірного руху по колу.

Основне завдання механіки полягає у визначенні положення тіла в будь-який момент часу. Положення матеріальної точки, що рухається по колу в будь-який момент часу t, можна визначити трьома способами:

1. Знаючи шлях, пройдений точкою від початкового положення до наступного, можна визначити положення тіла в момент часу t, відклавши від початкового положення вздовж траєкторії шлях S = Vt, (якщо відомо лінійну швидкість руху матеріальної точки, задано траєкторію тіла та його початкове положення).

2. За допомогою кута φ, на який повертається радіус-вектор. Якщо відомо кутову швидкість тіла, радіус кола й початкове положення тіла, то за поворотом радіус-вектора на кут φ = ωt визначаємо положення тіла.

3. За допомогою рівнянь руху в координатній формі. Оскільки рух по колу відбувається в одній площині, то для опису руху можна скористатися двовимірною системою координат. Якщо пов'язати точку початку координат з центром кола, по якому рухається тіло, а початкове положення тіла з'єднати з точкою перетину кола й осі Ох, то координати х та можна обчислити за формулами:

,  

Оскільки кут φ змінюється з плином часу за законом φ = ωt, то рівняння координати для рівномірного руху по колу має такий вигляд:

  

 

 

Приклади розв’язування типових задач.

1. Вагон котиться із сортувальної гірки. Які частини вагона рухаються, а які перебувають у стані спокою відносно: а) дороги; б) стін вагона.

Відповідь: відносно дороги рухаються всі точки вагона та його коліс; тільки точки коліс, які у цей момент дотикаються до залізничного полотна, перебувають у спокою. Відносно стін вагона рухаються всі точки коліс, окрім їхніх центрів.

 

2. Кран, повертаючись навколо власної осі, одночасно піднімає вантаж. Який вигляд матиме траєкторія руху вантажу: а) відносно землі; б) відносно кранівника?

Відповідь: а) відносно землі траєкторія руху вантажу є гвинтова лінія (вантаж одночасно рухається і по колу і в гору); б) відносно кранівника вантаж тільки піднімається, отже, його траєкторія – вертикальна пряма.

 

3. Хлопчик вийшов із будинку і пройшов прямими вулицями 2 квартали в напрямі на схід, а потім 2 квартали – на північ. Визначте шлях і модуль переміщення, якщо довжина кварталу 150 м.

Дано:    СІ    Розв’язання:

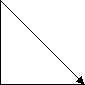a = 150 м   150 м    Позначимо шлях хлопчика

n_схід = 2      на схід відрізком АВ

n_півн = 2       АВ = а * n_схід ,

       тоді його шлях на північ – ВС.

 S = ?        ВС = а * n_півн

= ?       Відповідно пройдений шлях

       знаходимо як

S = АВ + ВС

   S = а * n_схід + а * n_півн

Переміщення в такому випадку відповідає відрізку АС.

= АС

S = 150 м * 2 + 150 м * 2 = 600 (м)

= 424,3 м

 

Відповідь: шлях 600 м, модуль переміщення 242,3 м.

4. За рівнянням руху х = -270+12t визначте початкову координату, швидкість руху тіла. Знайдіть координату тіла в момент часу t = 5с.

Розв’язання

З рівняння руху визначаємо: х₀ = -270 м, V_x = 12 v/c.

У момент часу t = 5с маємо: х = -270+12*5 = -210(м).

 

5. Вагон завширшки 2,4 м, який рухався рівномірно прямолінійно зі швидкістю 54 км/год, було пробито кулею, яка летіла перпендикулярно до напрямку руху вагона. Отвори від кулі у стінках вагона зміщені один відносно іншого на 6 см. Визначте швидкість руху кулі.

Дано:       СІ     Розв’язання:

d = 2.4 м        Задача пов’язана з відносністю руху

V = 54 км/год V = 15 м/c     вагона та кулі.

r = 6 см  r = 0,06 м     Час руху кулі, який ми вважаємо 

     V_к = ?        рівномірним прямолінійним (знехтуємо

         зміною швидкості кулі під час її взаємодії зі стінками вагона), у вагоні: , де V_к – швидкість руху кулі; час переміщення вагона на відстань r (саме під цим переміщенням зумовлено зміщення вхідного та вихідного отворів кулі): , де V – швидкість руху вагона.

Оскільки t₁ = t₂, то 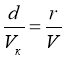, звідки .

Перевіримо одиниці вимірювання та визначимо числове значення шуканої величини:

;

 

 

 

 

 

 

 

 

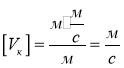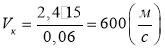
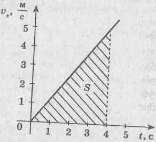
6. Рівняння руху матеріальної точки має вигляд х = 0,4t². Запишіть рівняння залежності швидкості руху тіла від часу його руху та побудуйте графік цієї залежності. Заштрихуйте на графіку площину, яка чисельно дорівнює шляху, пройденому точкою за 4с, і обчисліть її шлях.

Дано:   CI  Розв’язання:

х = 0,4t²    

t₁ = 4с     З рівняння х = 0,4t²

     х₀ = 0; V_0х = 0; а_х = 0,8 м/с²

V_x = V_x(t) - ?   Отже, V_х  = 0,8t

S_x = ? Побудуємо графік залежності проекції швидкості від часу

Обчислимо шлях матеріальної точки за формулою .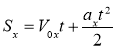

Оскільки V_0х = 0, то .

;  

Відповідь: V_х  = 0,8t;  S_x = 6,4м.

 

7. За 50 м до в’їзду на міст мотоцикліст, який до того рухався зі швидкістю 54 км/год., почав гальмувати. Гальмівне прискорення за модулем дорівнювало 2 м/с². Чи порушив водій правила, якщо перед в’їздом на міст є знак обмеження швидкості 10 км/год.?

Дано СІ               Розв’язання

υ_о  = 54      υ_о  = 15             

s = 50 м 0 s₂ х

а = 2      Щоб відповісти на запитання, поставлене у

υ  = 10      υ  = 2,8          задачі, можна, наприклад, знайти гальмівний

s_гальм - ?                                   шлях мотоцикліста.

 

Рух за умовою рівноприскорений, переміщення мотоцикліста може бути знайдене за формулою = або, враховуючи, що υ_0х= υ₀, а_х= - а, υ_х= υ, s_х = s, отримаємо:

=

Перевіримо одиниці й визначимо числове значення гальмівного шляху:

         

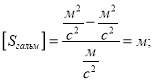
Бачимо, що необхідний гальмівний шлях більший за відстань, яка залишилася до мосту

Відповідь: мотоцикліст порушив правила руху.

 

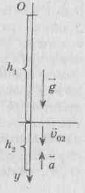8. Спортсмен, стрибнув із п’ятиметрової вишки, занурився у воду на глибину 2м. Скільки часу і з яким прискоренням він рухався у воді?

Дано:   СІ  Розв’язання:

h₁ = 5 м      Система відліку «Земля». Рух у повітрі -

h₂ = 2 м      вільне падіння (опором повітря

V₀₁ = 0 м/с       нехтуємо).

V₂ = 0 м/с      Оскільки V₀₁ = 0, то .

g = 9,8 м/с²       Швидкість, з якою вовк закінчує вільно

       падати, дорівнює швидкості, з якою він

a - ?       входить у воду (рис. 1).

t - ?       На другому відрізку (у воді) а_у = -а   Рис. 1.

       і кінцева швидкість дорівнює нулю (V₂ = 0).

.

,   ,   .

,      

    .

          

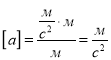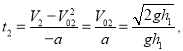
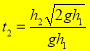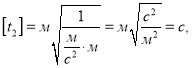
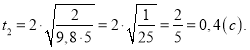
Відповідь: а = 25м/с², t = 0,4с.

 

 

9. Матеріальна точка рівномірно обертається по колу радіусом 10 м, здійснюючи повний оберт за 2 с. Визначте її обертову частоту, лінійну та кутову швидкості, доцентрове прискорення. Як зміниться доцентрове прискорення, якщо радіус траєкторії збільшити в N разів?

Дано:            СІ         Розв’язання:

R₁ = 10 м       Обертову частоту можна знайти через період , тобто

 T = 2 с       ν = 1/2с = 0,5 (Гц)

R₂ = N R₁          Кутову швидкість даної точки знайдемо за формулою ω=2πn                    ω = 2πν, отже ω=2·3,14·0,5 Гц = 3,14 рад/с.

 

n - ?       Лінійну швидкість доцільно визначити так:

ω - ?                                      

υ - ?

a_доц - ?       Таким чином,

- ?       Для визначення доцентрового прискорення використаємо формулу .

Перевіримо одиниці та визначимо числове значення шуканої величини:

Оскільки в умові нічого не сказано про зміну лінійної та / або кутової швидкості, то коректно відповісти на запитання про зміну доцентрового прискорення при зміні радіусу траєкторії не видається можливим. Однак ми можемо розглянути два випадки.

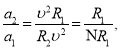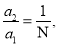1.     Якщо при зміні радіусу траєкторії не змінилася лінійка швидкості руху, то отже, тобто доцентрове прискорення зменшиться в N разів.
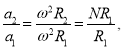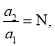2.              Якщо ж при зміні радіусу траєкторії незмінною залишиться кутова швидкість, то, виражаючи доцентрове прискорення через кутову швидкість (а_доц = ω²R), матимемо: отже, тобто в цьому випадку доцентрове прискорення зросте в N разів.

Запитання для перевірки теоретичних знань з теми «Кінематика»

1. Дайте означення механічного руху. Наведіть приклади механічного руху.

2. Які види механічного руху ви знаєте?

3. У чому полягає основна задача механіки? її розв’язання? Наведіть приклади практичного застосування розв’язання основної задачі механіки.

4. Дайте визначення матеріальної точки.

5. Що називають системою відліку? Чим вона відрізняється від тіла відліку?

6. Що беруть за тіло відліку, коли кажуть: а) автомобіль рухається зі швидкістю 100 км/год; б) провідник іде по вагону зі швидкістю 4 км/год; в) Земля рухається по своїй орбіті зі швидкістю 30 км/год?

7. Автомобіль рухається по дорозі. Назвіть системи відліку, які дозволяють описати його рух. В якій системі відліку він буде нерухомий?

8. Дайте визначення траєкторії руху, шляху та переміщення.

9. Яким може бути механічний рух за формою траєкторії?

10. Коли модуль переміщення та пройдений шлях збігаються?

11. Чи залежить траєкторія руху тіла від системи відліку?

12. У чому полягає зміст поняття відносності руху?

13. Який рух називають рівномірним?

14. Який рух називають рівномірним прямолінійним?

15. Що таке швидкість? Чому швидкість – векторна величина?

16. Назвіть одиниці вимірювання швидкості.

17. Який вигляд має графік швидкості при рівномірному прямолінійному русі?

18. Як за графіком швидкості обчислити переміщення тіла?

19. Який вигляд має графік залежності координати від часу для прямолінійного руху?

20. Який вигляд має графік пройденого шляху? Від чого залежить кут нахилу прямої графіка?

21. Яку систему відліку можна назвати рухомою? нерухомою?

22. Сформулюйте закон додавання швидкостей.

23. Дайте визначення прискорення.

24. Який рух називають рівноприскореним?

25. Дайте визначення прискорення. Чи змінюється прискорення при рівноприскореному русі?

26. В якому випадку проекція прискорення має додатне, а в якому від’ємне значення?

27. Як записати кінематичне рівняння рівноприскореного руху? Чим воно відрізняється від рівняння переміщення?

28. Дайте визначення вільного падіння тіла? Наведіть приклади.

29. Який це рух? Чому?

30. Яку суперечність виявив Галілео Галілей?

31. В чому полягає сутність досліду Галілея?

32. Як можна довести, що прискорення вільного падіння не залежить від маси тіла? Від чого воно залежить?

33. Чому прискорення вільного падіння різне на різних широтах Землі?

34. Чи однаковим буде час падіння тіл різної маси з однакової висоти? За яких умов час падіння буде однаковим?

35. Чому дорівнює прискорення тіла, кинутого вертикально вгору, у верхній точці траєкторії?

36. З однієї точки падають без початкової швидкості два тіла з інтервалом часу t секунд. Як рухаються ці тіла одне відносно одного в польоті?

37. Як напрямлені вектор прискорення і вектор швидкості тіла, кинутого вертикально вгору?

38. Чому дорівнює швидкість тіла, кинутого вертикально вгору, у найвищій точці його польоту?

39. Чи зміниться прискорення тіла, що вільно падає, якщо йому надати початкової швидкості?

40. Поясніть, чому швидкість тіла, кинутого вертикально вгору, змінюється.

41. Назвіть характеристики руху по колу.

42. Дайте визначення лінійної швидкості. В яких одиницях вона вимірюється?

43. Дайте визначення кутової швидкості. В яких одиницях вона вимірюється?

44. Дайте визначення періоду обертань. В яких одиницях він вимірюється?

45. Дайте визначення частоти обертань. В яких одиницях вона вимірюється?

46. Дайте визначення доцентрового прискорення. В яких одиницях воно вимірюється?

47. Чому будь-яку криволінійну траєкторію можна частково представити рухом по колу?

48. Чому виникає доцентрове прискорення? Який воно має напрямок?

49. Чи однакове доцентрове прискорення точок, які віддалені від центра обертання на різну відстань?

50. Як розв’язати основну задачу механіки для рівномірного руху по колу.

 

Якісні задачі для самостійного розв’язання.

1. У певній системі відліку координата х залишається незмінною. Чи обов’язково тіло є нерухомим у цій системі відліку?

2. Маленькій дитині здається, що секундна стрілка годинника рухається, а годинна і хвилинна стрілки нерухомі. Як довести дитині, що вона помиляється?

3. Міжпланетна станція здійснює переліт Земля-Марс. Чи можна вважати її матеріальною точкою: а) під час оцінювання ризику зіткнення з метеоритом; б) у процесі обчислення часу польоту; в) у процесі вивчення розігріву станції під час руху в атмосфері Марса?

4. Людина їде в автомобілі. Назвіть тіла відносно яких людина перебуває в стані спокою, а відносно яких рухається.

5. У фільмі «Швидкість» пасажирів автобуса, який рухається зі швидкістю 120 км/год, евакуюють на авто платформу, яка їде поряд з автобусом. У стані спокою чи руху перебуває платформа у системі відліку, пов’язаній: а) з поверхнею землі; б) з автобусом? Чому дорівнює швидкість руху авто платформи у цих системах відліку?

6. Під час стоянки потяга з верхньої полиці купе хлопчик упустив м’яч. Чи може м’яч впасти на те саме місце, якщо хлопчик упустить м’яч під час руху потяга? Відповідь обґрунтуйте.

7. За якої умови шлях дорівнює модулю переміщення? Чи може модуль переміщення бути більшим від пройденого шляху?

8. Шлях чи переміщення оплачує пасажир автобуса?

9. Прямолінійною ділянкою залізниці рухається потяг. Які його частини рухаються прямолінійно, а які криволінійно?

10. Наведіть приклади прямолінійних рухів.

11. Наведіть приклади криволінійних рухів.

12. Що ви можете сказати про траєкторію руху тіла, якщо переміщення цього тіла дорівнює нулю?

13. Диск обертається в горизонтальній площині. Від його центру до краю котиться кулька. Який вигляд має траєкторія руху кульки відносно: а) диска; б) землі?

14. Один автобус, вийшовши із гаража, здійснив до повернення 10 рейсів, а другий – 5 рейсів за тим самим маршрутом. Який із них пройшов більший шлях? Здійснив більше переміщення?

15. У довільному порядку наведено рухомі об’єкти: пішохід іде вулицею, звукові хвилі поширюються у повітрі, молекула водню при 0⁰С, слабкий вітер, електромагнітні хвилі у вакуумі, штормовий вітер. Розташуйте об’єкти у порядку зростання за їхніми швидкостями використовуючи попередньо набуті знання.

16. Швидкість руху м’яча відносно вагона 2м/с, швидкість руху вагона відносно Землі 3м/с. Якою може бути швидкість руху м’яча відносно Землі?

17. На першому метрі руху від старту бігун досяг швидкості 2м/с. Чи дорівнюватиме його швидкість на другому метрі при сталому прискоренні 4м/с?

18. Чи можна застосовувати формулу для визначення швидкості падіння тіла з висоти 5км на поверхню Землі? Юпітера? Сонця?

19. Чому дорівнює період обертання секундної стрілки годинника? хвилинної? годинної?

20. Секундна стрілка вдвічі коротша за годинну. У якої з них лінійна швидкість руху кінця стрілки більша? У скільки разів?

 

 

 

 

 

 

 

 

Розрахункові задачі для самостійного розв’язання

Середній рівень

1. М’яч упав з висоти 2 м, відскочив на 1 м угору, знову впав і після відскоку був упійманий на висоті
0,5 м. Знайдіть шлях і модуль переміщення м’яча.

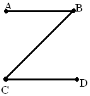
2. За даною траєкторією руху тіла (рис. 1) знайдіть його переміщення, якщо початкова траєкторія А, а кінцева – D.               Рис. 1.

Задачу розв’яжіть графічно. 

3. Вертоліт, пролетівши в горизонтальному напрямку 40 км, повернув під прямим кутом і пролетів ще 30 км. Визначте шлях і модуль переміщення вертольоту.

4. Вагон, рухаючись під ухил, подолав 120 м за 10 с. Скотившись з гірки, він пройшов до повної зупинки ще 360 м за 1,5 хв. Визначте середню швидкість руху вагона.

5. Реактивний літак здійснює посадку на аеродром, маючи швидкість 324 км/год. Скільки часу пройде до його зупинки, якщо літак рухається з прискоренням 9 м/с²?

6. Тролейбус, рухаючись зі швидкістю 18 км/год, зупинився за 4 с. Визначте прискорення його руху та гальмівний шлях тролейбуса.

7. Залежність швидкості руху тіла від часу має вигляд: υ_х = 2 + 1,5t. Охарактеризуйте рух тіла та визначте параметри цього руху.

8. За графіками залежності а_х(t) (рис. 2) для кількох тіл (див. рисунок) охарактеризуйте рух кожного тіла, якщо початкові швидкості руху всіх тіл однакові, напрямлені у бік осі ОХ і мають значення 5 м/с.         Рис. 2.

9. Кульку кинули вертикально вгору зі швидкістю 25 м/с. На яку максимальну висоту відносно точки кидання вона підніметься?

10. Хлопчик обертає кульку, прив’язану до нитки, з частотою 5 Гц. Визначте період обертання кульки.

11. Під час обертання вала радіусом 10 см доцентрове прискорення для точок на його поверхні становить 10 м/с². Визначте кутову швидкість обертання вала.

 

 

Достатній рівень

1. Дівчинка проходить шлях від будинку до школи 250 м, а до музичного театру в тому ж напрямку — 670 м. Який шлях проходить дівчинка до музичного театру, якщо вона йде не з будинку, а прямо зі школи.

2. Велосипедист, рухаючись по коловому велотреку, подолав півкола. Яке переміщення здійснив велосипедист, якщо пройдений ним шлях дорівнює 157 м? Виконайте пояснювальний рисунок.

3. Кінь у мультику «Ну, постривай!» (рис. 1.), рухаючись ареною цирку, пробігає коло діаметром 14 м за 40 с. Визначте шлях і модуль переміщення коня: а) за 40с; б) за 20 с; в) за 60 с; г) за 10 с руху. Виконайте пояснювальні рисунки.

Рис. 1.          4. Тіло перемістилось із точки А в точку В (рис. 2). Зобразіть вектор переміщення, визначте його модуль і проекції на координатні осі, якщо 2 клітинки на рисунку відповідають 20 м.                                                        

5. Яку відстань подолає літак за 1,5хв, якщо він летить              Рис. 2.

зі швидкістю 800км/год?

6. Ескалатор метро рухається зі швидкістю 0,75 м/с. За який час пасажир піднімається по ескалатору завдовжки 50 м, якщо він іде в напрямку його руху зі швидкістю 0,25 м/с відносно стрічки ескалатора?

7. Рухаючись рівно скорено зі стану спокою, вантажівка на деякій відстані набула швидкості 36 км/год. Яку швидкість вона мала посередині цього шляху?

8. За 5 с швидкість руху мотоцикліста збільшилась від 36 км/год до 54 км/год. За яким прискоренням він рухався? Запишіть формулу залежності швидкості від часу і побудуйте відповідний графік, якщо мотоцикліст рухався рівноприскорено

9. Рухи двох автомобілів описуються рівняннями: х₁ = 5t+2t² і х₂ = 80-7t. Визначте: а) де й коли вони зустрінуться; б) відстань між автомобілями через 5 с після початку руху. Розв’яжіть задачу аналітично і графічно.

10. Тіло, яке було кинуте з поверхні землі вертикально вгору, впало через 6 с. На яку максимальну висоту воно піднялось?

 

 

Високий рівень

1. Під час зміни варти в королівських покоях мушкетер пройшов коридором 10 м, повернув праворуч і пройшов 20 м, повернув ліворуч і пройшов 10 м, повернув ліворуч і пройшов 50 м, повернув праворуч і пройшов 20 м. Лише після цього він виструнчився і завмер. Накресліть у зручному масштабі траєкторію руху мушкетера. Який шлях він пройшов? Яке переміщення здійснив?

2. Рух двох велосипедистів задано рівняннями х₁ = 5t і х₂ = 150-10t. Визначте час і місце зустрічі велосипедистів: а) аналітично, б) графічно.

3. Координата тіла, яке рухається вздовж осі ОХ, змінюється відповідно до рівняння х = 8+5t-1,25t². Визначте параметри руху, охарактеризуйте його та побудуйте графік залежності V(t).

4. Між двома пунктами, які розташовані на відстані 100 км один від одного, річкою курсує катер, який долає цю відстань за 4 год, якщо пливе за течією, і за 10 год. – якщо проти течії. Визначте швидкість течії та швидкість руху катера відносно води.

5. Пліт завдовжки 16 м пливе річкою зі швидкістю 0,8 м/с. Вздовж плота рівномірно рухається людина, яка за 20 с проходить його від одного краю до іншого і повертається назад. Знайдіть швидкість руху, переміщення та пройдений людиною шлях: а) відносно плота; б) відносно берега.

6. Вершник за перші 40 хв проскакав5 км. Наступну годину він рухався зі швидкістю 10 км/год, а решту 6 км шляху – зі швидкістю 12 км/год. Визначте середню швидкість вершника: за весь час руху, за першу годину руху та на першій половині шляху.

7. Потяг, що відходить від станції, проходить за третю секунду 2,5 м, рухаючись рівноприскорено. Визначте переміщення, яке здійснив потяг за сьому секунду.

8. Тіло кинули з висоти 200 м з початковою швидкістю 2 м/с. Протягом якого часу падало це тіло?

9. Диск обертається з кутовою швидкістю 3 рад/с. Відносно диска по радіусу рухається тіло зі швидкістю 0,4 м/с. Знайдіть швидкість руху цього тіла відносно Землі, коли воно буде на відстані 10 см від осі обертання.

10. Скільки обертів зробить дзиґа, яка обертається з частотою 251,2рад/с, за час її вільного падіння з висоти 5 м?

          Додаток 1.

          Таблиця 1.

Назва графіка	Графік	Опис графіка
Графік проекції прискорення ах = ах(t)		Прискорення рівноприскореного рух є величина стала, тому залежність проекції прискорення від часу – пряма, паралельна осі часу t. Якщо проекція додатна, то пряма розміщується над віссю, якщо від’ємна – під нею.
Графік проекції швидкості Vx = Vx(t)		Лінійна залежність проекції швидкості від часу є лінійною функцією Vx = V0х  ± ахt. Отже, залежність проекції швидкості від часу – пряма, що розміщується під кутом до осі часу t і перетинає вісь ординат на відстані V0х  від початку координат.
Графіки проекції переміщення Sx = Sx(t) та координати x = x(t)		Кінематичне рівняння переміщення й координати від часу є квадратичними рівняннями       та                  . Тому графіками залежностей проекції переміщення і координати є параболи, вітки яких згідно з параметрами руху мають різний вигляд (випадки а і б).

 

          Додаток 2.

          Таблиця 2.

	Рівноприскорений рух	Вільне падіння	Рух тіла кинутого в гору
Рівняння швидкості у векторній формі
Рівняння швидкості у скалярній формі
Рівняння координати
Рівняння переміщення у векторній формі
Рівняння переміщення у скалярній формі

 

 

 

 

          Додаток 3.

          Таблиця 3.

Величини, які пов’язує формула	Формула
Період і частота	і
Кутова швидкість і період
Кутова швидкість і частота
Лінійна швидкість, період, радіус кола
Лінійна швидкість, частота, радіус кола
Лінійна швидкість, кутова швидкість, радіус кола

 

Список використаних джерел

1. Коршак Є.В., Ляшенко О.І., Савченко В.Ф. Підручник для середньої загальноосвітньої школи Фізика 9 клас. – Київ; Ірпінь: ВТФ «Перун», 2001. – 232с.

2.  Фізика:Навчально-практичний довідник / Ю.А.Соколович, Г.С.Богданова. Харків: «Ранок», 2012. – 384с.

3.  Фізика. 10клас: підручник для загальноосвітніх навчальних закладів: рівень стандарту / Л.Е.Генденштейн, І.Ю.Ненашев. – Харків: Гімназія,
2010. – 272с.

4.  Фізика. 10 клас. Академічний рівень: Збірник задач / О.О.Карпухіна, Ф.Я.Божинова, В.В.Хардіков. – 2-ге видання, перероблене і доповнене. Харків: «Ранок», 2011. – 288с.

5.  Педагогічний програмний засіб «Физика 9-11 класс. Экспресс подготовка к экзамену». Новая школа, 2006.